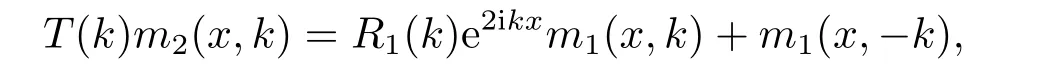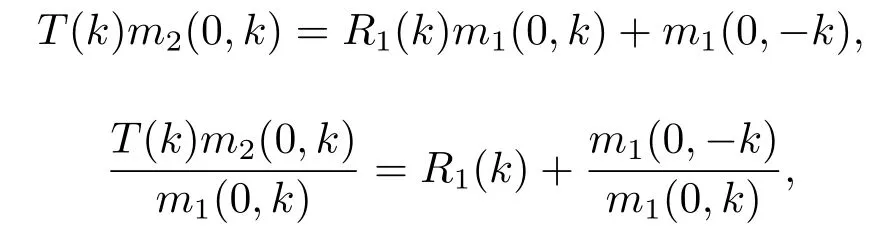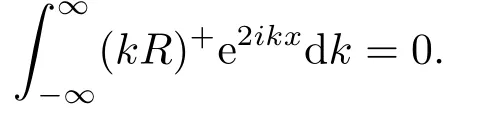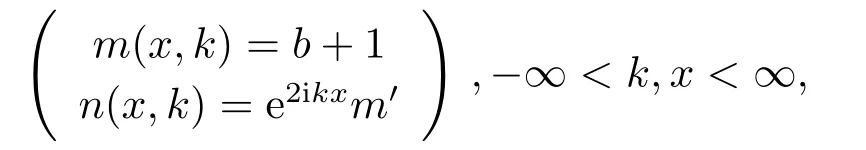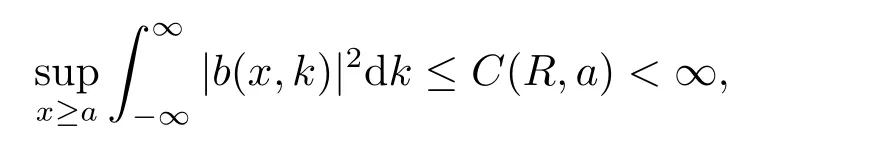带磁场的一维Schrdinger方程的逆散射问题
胡振宇,黄华,段志文
( 华中科技大学数学与统计学院,湖北 武汉430074)
1.引言

研究其逆散射问题,其中p(x)为实位势,并且无有界态.本文给出了该逆散射问题的解.H是算子延拓至L2(−∞,∞),即H是自伴Schrdinger 算子.记空间:
Deift[3]等人研究了一维Schrdinger方程:−f′′+qf=k2f的逆散射问题,得出以下结论:令f1(x,k),f2(x,k),k ∈R{0}是方程Hfj=k2fj,j= 1,2的解,且有如下的渐近状态:f1(x,k)→e−ikx,x →+∞,f2(x,k)→e−ikx,x →−∞,且f1(x,k),f2(x,k)有如下的渐近表示:

其中Ti,Ri,i=1,2,分别是传输系数和反射系数.定义矩阵

此外,Faddeev[5−6]在Schrdinger方程逆散射问题上做了类似的工作,并提出自己的一套方法.而他的方法源于Gel’fand-Levitan[7],Kay-Moese[8]和Agranovich-Marchenko[1]等人的工作.
本文受这些文章的启发,添加磁场位势,研究该磁场位势的逆散射问题,也得到类似的结论.本文研究思路如下:对方程(1.1)做如下变换:m(x,k) = e−(ϕ+ikx)f(x,k)→1,x →+∞,可得

或改写成方程组的形式:

且

记−p2(x)=QR(x,m),即

在方程组(1.2)中我们通过公式(1.3)消去p.为了重构p,我们仅需要求解方程组(1.4)的初值问题[2]的解,那么p可由(1.3)式给出.本文的主要内容安排如下:在第二部分,本文推导了关于散射矩阵S(k),m(x,k),B(x,k)的相关结论.第三部分,在位势p无界态的条件下,本文推导了迹公式,并通过求解初值问题(1.4),由反射系数R重构p,并且还得到了方程组(1.4)解的先验上界.
2.正问题
在叙述本文的研究方法之前,给出一些相关引用、定义及事实.定义R上的Fourier 变换及其逆变换:
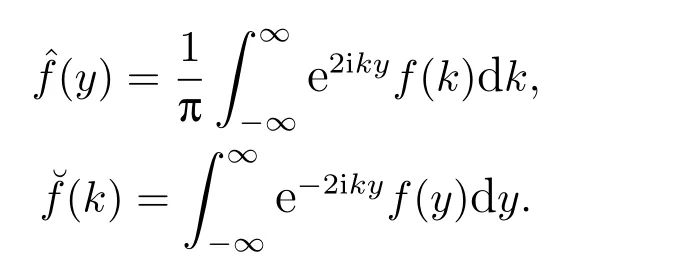
H2+表示由Hardy空间[4]中解析函数h(k)构成的集合,其中Imk >0,h满足若假设h(k)∈H2+的边界值为在L2(−∞,∞) 意义下,即有如下等价H2+空间的描述:

根据前文介绍,下面引理和定理当它们的证明和文[3]相似时,只作叙述,证明略去.而当本文相关结论证明方法和他们不同时,加以详细论证.
引理2.1[3]对于每个k,Imk ≥0,积分方程

有唯一解m(x,k),且m(x,k)满足如下的Schrdinger方程:

且m(x,k)→1当x →+∞,m(x,k)服从如下估计式:
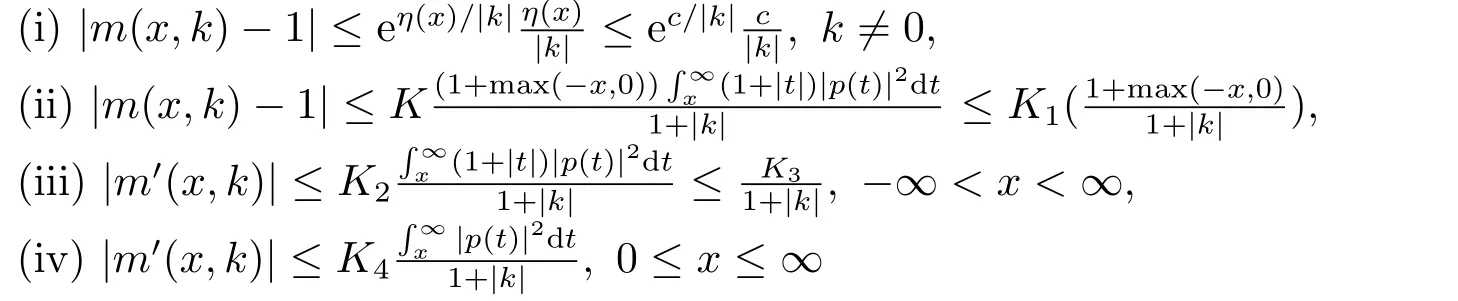
对于每个x,当Imk >0,m(x,k)是解析的且当Imk ≥0,m(x,k)是连续的.特别地,由(ii) 知,m(x,k)−1∈H2+.此外,记˙m(x,k)≡dm(x,k)/dk在Imk ≥0时存在,k≠ 0时k˙m(x,k)在Imk ≥0 时处处连续.若p ∈L21,那么˙m(x,k)在k=0 处也存在且连续,且有如下估计式:
(v)|(x,k)|≤c(1+x2)对于所有k ≥0,p ∈L21.其中
引理2.2[3]对于任意x,当Imk ≥0,m(x,k)有有限个零点,并且它们均为简单零点,在负半轴上.若k= iβ(β >0)是m(x,k)的零点,那么k2=−β2是算子在L2(x 引理2.3[3]方程 y ≥0,有一个(实的、唯一)解B(x,y)满足 特别地,B(x,y)∈L1∩L∞(0 B(x,y)关于x和y均连续且有: B(x,y)满足波动方程: 且有−∂B(x,0+)/∂x=−∂B(x,0+)/∂y=−p2(x).最后,m(x,k)≡1+∞0B(x,y)e2ikydy即为引理2.1中的函数. 引理2.4[3]假设是相应约斯特函数的Fourier变换,j=1,2.令 则 可得L∞(0 由此即得L1(0 定理2.1令p(x)是上的实位势,那么 对于所有k≠0是连续的(若p(x)∈L21,那么S(k)在k=0连续)且有如下性质: 1) (对称性)T1(k)=T2(k)≡T(k), 2) (酉性质) 故 3) (解析性)T(k)在Imk >0时是亚纯函数且有有限个简单极点iβ1,··· ,iβn,βj >0,在虚拟k轴上,剩余项是 数−β21,··· ,β2n是H的特征值.当Imk >0,k≠ 0,iβ1,··· ,iβn,T(k)连续(若p(x)∈L21,那么当Imk ≥0,k≠iβ1,··· ,iβn,T(k)连续). 4) (逼近) (i)T(k)=1+O(1/k) 当|k|→∞,Imk ≥0, (ii)Rj(k)=O(1/k),j=1,2,当|k|→∞,k是实数, (iii) 若H没有特征值,那么T(k)−1∈H2+且|T(k)|≤1在Imk ≥0. 5)|T(k)|>0对于所有Imk ≥0,k≠0,|k|≤C|T(k)|当→0,若p(x)∈L21,有两种可能情形: (i) 0 (ii)T(k) =αk+o(k),α≠ 0,当k →0,Imk ≥0,且1+Rj(k) =αjk+o(k),j= 1,2当k →0,k实. 证该定理1),2),4),5),6)的证明可参考文[3]中的定理2.1,只证明3).极点k0使得0,即k0为T(k)的极点.下证iβj,j=1,2,··· ,n是简单极点. 令k=iβ(T−1(iβ)=0),故 下面计算[f1,˙f2](x),[ ˙f1,f2](x),由方程:−f′′2−2ipf′2−ip′(x)f2=k2f2得 该方程为常微分方程,则有: 则 因为eϕf1(x,iβj) 是实值非零,且与eϕf2(x,iβj) 线性相关,故(T−1)·(iβj)≠0.即得证iβj,j=1,2,··· ,n是简单极点,且有剩余项: 3)得证. 引理2.5[3] 能被R1(k)(或R2(k))和特征值−β21>···>−β2n重构. 引理2.6[3]令H有n个界态:0>−β21>···>−β2n,且有相应的规范常数: 那么 引理2.7[3]对于定理2.1中的散射矩阵S(k),有 并且 引理2.8[3](i) 若p ∈L21/2,则 (ii) 若p ∈L21/2,且(p)′ ∈L21/2,则 引理2.9[3](虚拟水平集)H有一界态当且仅当m(x,0)=0对于某些x. 在这一节我们将论述如何通过反射系数和规范常数来重构位势.另外除非特别说明,我们现考虑p ∈L21/2且p′ ∈L21/2.关于p的这些光滑性假设仅仅为了便于阐述最小化技术方法.特别地,通过定理2.14)(ii) 我们注意到kR(k)∈L1∩L∞⊂L2.由文[1] 知,通过引理2.8我们可得,当p无界态时有: 该式我们称之为迹公式. 在下面证明中,方程(1.4)将对应如下初值条件 引理3.1[3]令p(x)无界态,能通过选取R(k)使得那么p能被它的反射系数R(k)重构出来. 引理3.2[3]令|r(k)|<1即r(k)=O(1/k),且假定m(x,k)−1和r(k)e2ikxm(x,k)+m(x,k)−1均属于C(R,H2+).令b(x,k)=m(x,k)−1,我们有: (ii)令r(k)在0处连续且选取δ使得且假定1,那么 (iii) 令a>0,r(k)满足(ii)中条件,选取δa >0.使得对|x|≤a,选取则 定理3.1假设p(x)∈L21(0,∞)无界态(半直线)且无虚拟水平,那么p(x)能被它(半直线上的)的散射矩阵S(k),−∞ 证该定理证明分以下两步,首先得到公式 而全直线上的反射系数R可以视为限制在(0,∞),故只需考虑半直线(0,∞) 上反射系数R即可,然后由引理3.1可重构p(x).详细叙述如下:为了便于叙述,我们再次对p2(x) 作同样的正则性假设:(p2)′ ∈L1(0,∞).我们假设,当m(0,0)≠0 时,即p(x)无虚拟水平集.核心想法是将半直线问题拓展成全直线上去.由引理2.9可得到这样一个事实:p(x)在(0,∞)上能延拓至全直线并且有(p2)′ ∈L1(−∞,∞) 且无有界态.又m(x,0)≠0,x >0,因此大于0,p(x)可能在(−∞,0)上被重构.对于所有k, 其中R1(k),T(k)分别为反射系数,传输系数,且特别地, 或者 即 然而T(k)m2(0,k)/m1(0,k)−1∈H2+,因此R−= (1−S)−,即R−能由散射矩阵S重构.同样地,当x ≥0,(kR)−能由散射矩阵S重构. 同理可得: 即 定理3.2令p(x)∈L21是无界态的位势,那么 是方程(1.4)(3.1)的解且有: 其中C(R,a)仅依赖于反射系数R和点a. 证证明分为以下三步:首先通过引理2.1、2.6及定理2.1得到m(x,k)−1和r(k)e2ikxm(x,k)+m(x,k)−1均属于C(R,H2+),其次,易知是方程(1.4)(3.1) 的解,最后可由引理3.2推导出 得证. 总结在p(x)无界态且在L21中时,我们得该位势能被反射系数R(k)确定,并且得到基于R(k)的迹公式.另外,由此代入到原Schrdinger方程中,可以得到方程的解有上界.





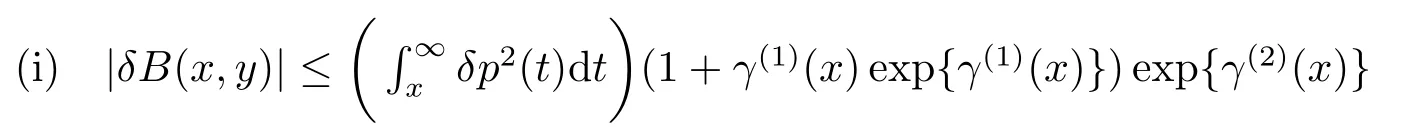


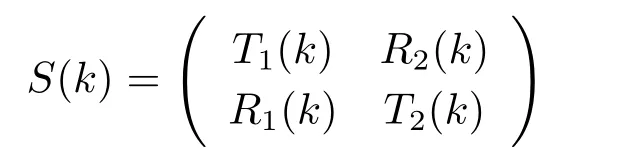
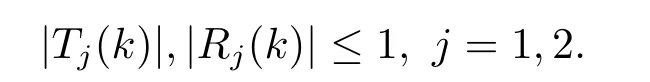

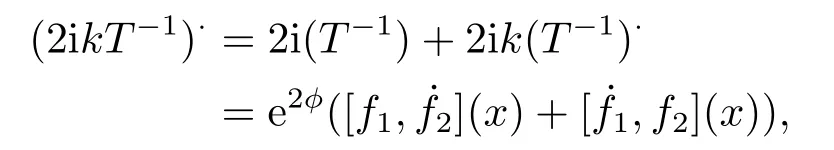




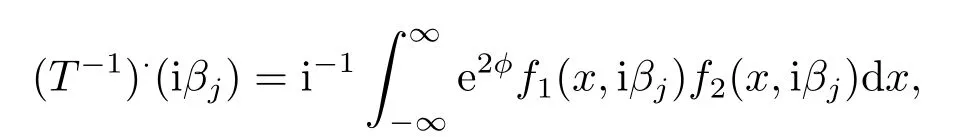
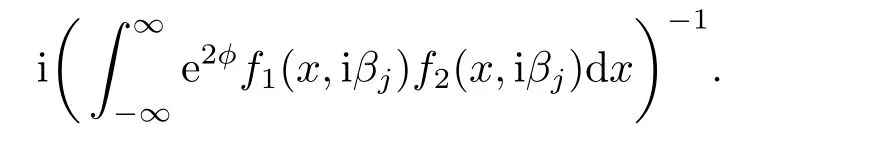



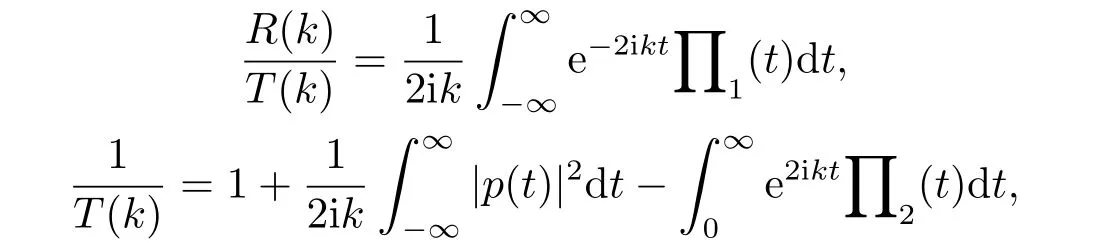



3.重构与迹公式