一类带Hardy-Sobolev临界指数的非局部问题正解的存在性

王跃,叶红艳,索洪敏

(贵州民族大学数据科学与信息工程学院,贵州 贵阳550025)

1.引言和主要结果

本文研究如下一类带Hardy-Sobolev 临界指数的非局部问题

其中Ω是R3中的光滑有界域,常数a,b>0,参数λ>0,f(x,u) 是Ω×R 到R 的连续函数.

含Hardy-Sobolev 临界指数的问题在国内外已有大量的研究成果.例如,问题

正解的存在性在[1-3]等文献中都有研究,Ω通常是RN中的光滑有界域或等于RN(N是正整数).当取a=λ=1,b=0时,问题(1.2)便成问题(1.1)的一种特殊情形,因此问题(1.1)在理论上具有一定的研究意义.更多带有Hardy-Sobolev临界指数时正解的存在性及多重性问题的最新研究还可以从文[4-6]及其引用文献中找到.另一方面,问题

仍然含有非局部项.通过文献检索,Dirichlet 边界条件下问题(1.3) 的研究近年来很受关注.如文[7]通过变分方法和山路引理获得f(x,u) =|u|p−2u时非平凡非正解和非平凡非负解的存在性,其中Ω ⊂RN是光滑有界域,N ≥3 时N= 1,2时2∗= +∞;文[8]考虑了f(x,u) =fλ(x)|u|p−2u时解的多重性,其中Ω ⊂RN(N ≥3) 是光滑有界域,文中获得fλ(x)∈L∞且1

则把u定义为问题(1.1)的弱解(简称解),其中Ω ∇u∇vdx=⟨u,v⟩表示H10(Ω) 上的内积,本文的主要结果如下:

定理1假设a,b,λ>0 且f(x,u) 满足如下条件:

(f1)如果f(x,u)≥0且存在s<5使对x ∈Ω一致成立;

(f2)存在µ>4使|u|>0时对x ∈Ω有那么,问题(1.1)至少有一个正解.

2.预备知识

考虑泛函

则对任意的v ∈H10(Ω) 有

根据文[3]中定理3.1可知Ω= R3时A可取到.通过截断技巧直接计算可得,对任意的正实数ε都存在对应的函数及正常数C1,C2,C3满足

引理2.1若a,b,λ>0,(f1)和(f2)成立,那么对任意I满足(PS)c条件.

证设{un}是I的(PS)c序列,则有

再由条件(f2)有

因此由Sobolev嵌入不等式可知{un}有界,从而存在u ∈H10(Ω) 及{un}的子列(不妨仍记为{un})使得n →∞时: 在H10(Ω)中un ⇀u;在Lp(Ω)(1≤p <6)中un →u;对任意x ∈Ω,几乎处处有un(x)→u(x).由(f1),对任意ε>0,存在常数mε,M >0,sε >s+1 使得

根据un ⇀u和Lebesgue 控制收敛定理(文[13]第27页),对任意ε>0 都有

设ωn:=un −u,则n →∞时‖ωn‖→0.若不然,总可以假设存在一个{ωn}的子列(不妨仍记为{ωn}) 使得并且

由Br´ezis-Leib引理(文[14]定理1) 和文[3]的引理4.3可知

根据(2.4)-(2.9)式可得

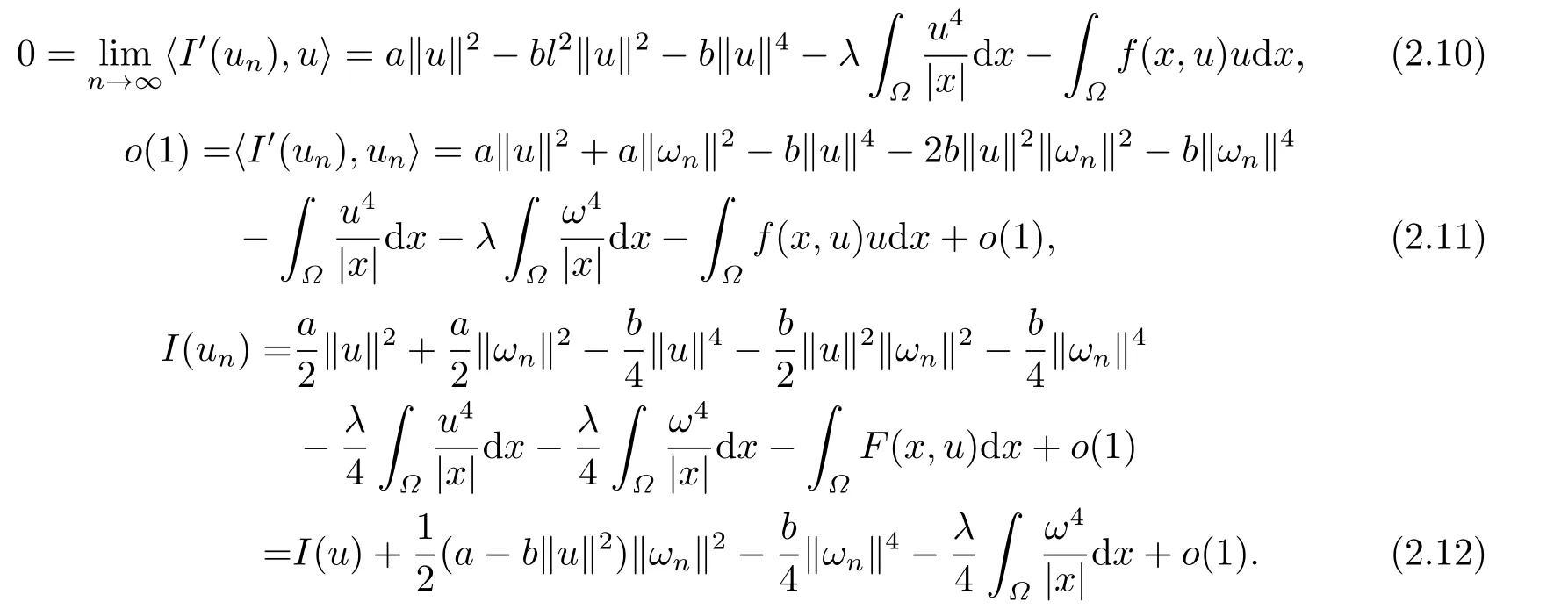
再由(2.10)-(2.11)式,Hardy-Sobolev 嵌入不等式及(f2) 可得

因此

根据条件(f2),可取ε >0 较小使得当|u| ≤ε时当|u|>ε时f(x,u)u −4F(x,u)>0,从而将(2.13)式代入泛函(2.1)得

另外,从(2.12)-(2.14)式和Hardy-Sobolev嵌入不等式可得出

引理2.2如果a,b,λ>0,(f1) 和(f2) 成立,则存在常数ε0>0,对任意的ε ∈(0,ε0) 及t ∈R 总有

证显然成立.当|u|>0 且|t|>0 时由条件(f2) 可知,存在正常数C4使得F(x,u)≥C4|u|µ,再根据(2.3),存在正常数C5,C6使得

根据条件(f2)可知µ>4,故存在对任给的ε ∈(0,ε0),总有从而

3.定理1的证明

由(f1),当|t|较小时有从而存在时有

此时

由(f2)有而故存在e ∈H10(Ω)满足使得

从而泛函I满足山路结构.设

由(3.1)和(3.2)可知I(τ(0))=0,I(τ(1))≤0.而(2.1)-(2.2)表明I(τ(t))∈C1([0,1],H10(Ω)),从而因此通过引理2.2可得

根据山路引理(文[15]定理2.1,定理2.4),存在{un}⊂H10(Ω)使得n →∞时I(un)→c,I′(un)→0.再由引理2.1可知I满足(PS)c条件,因此c是I的一个临界值.即存在u ∈H10(Ω)使得I(u) =c>0,I′(u)=0.从而u是问题(1.1)的一个非平凡解.此时在(2.2)中取v=u有0,而根据条件(f1)可得f(x,u)≥0,因此再根据极大值原理可得出u可以为正解.定理证毕.