区间数相似度计算模型及其应用研究

龚日朝，谭可星，潘芬萍

(湖南科技大学 商学院，湖南湘潭，411201)

由于客观事物的复杂性和人们认知的有限性与模糊性，在工程和管理评价与决策过程中，用区间数刻画事物定量属性特征大小是一种符合统计学原理和人们认知模糊性的有效方法。为了解决现实中不确定环境下用区间数刻画的事物的相似性，如多个区间数刻画的同属性对象的分类或比较，或众多评价者用区间数对同一个事物进行评价的集中度等相似性问题，学术界提出了区间数相似性概念［1］。其中，相似性测度在不确定环境下的决策过程中起着非常重要的作用，因此，许瑞丽等提出了区间数相似度［2］、区间数的几何距离、高度和回转半径等概念［3］，逐步形成了很多相似度分析的基本理论和方法，并在工程实践评价、社会经济管理绩效评价或管理决策领域得到了普遍的应用［4－19］。

在理论上，自区间数相似度概念提出后，很多学者提出了其测度模型，如:许瑞丽等［2］提出了两区间交集占两区间并集的长度比例的测度模型;CHEN S J等［20］提出了基于映射距离算子的相似性度计算公式。同时，李秉焱等［21］在研究区间数刻画的多专家多属性决策问题中也提出了区间数相似度的测度方法，并给出了其相似性的期望性质与基于区间数相似度的群决策方法。该方法通过OWA算子对专家意见进行归纳，通过将备选方案与正、负理想方案进行比较，实现了备选排序。LIU G F等［22］利用模糊集的贴近度理论，给出了三元区间数的公理化定义，将区间数推广到三元区间数，得到了相应的相似度计算公式。并针对属性值为三元区间数且权重和属性值不完全的多属性决策问题，根据传统TOPSIS法的基本思想，提出了三元区间数相似度的决策方法。

在应用上，姜艳萍等［23］将区间数相似度计算模型应用于森林火灾应急响应方案的选择，取得了很好的成果;WANG H［24］针对模式识别领域中的特征选择，引入区间数相似度的概念，提出了一种连续的特征选择方法。该方法基于区间数的相似度，将每个特征的属性相似度重新定义为特征选择的启发式信息。然后，通过对特征语料库的排序来实现特征子集的选择。在UCI数据库数据集上的实验表明，该方法极大地提高了连续特征分类的有效性和效率。XIAO Y I等［25］基于区间数相似度，对分布式多目标跟踪系统中的本地传感器的异步航迹关联方法进行了研究，通过区间数序列变换(IRST)对包含区间数据和真实数据的同一长度序列进行定义，定义新的序列差分测量方法，获得用相关度刻画的轨迹关联结论，有效地解决异步跟踪航迹关联问题。孟志华［26］将区间数相似度理论应用于企业运营绩效的多指标评价，构建了基于TOPSIS法的多属性评价模型，将理论运用到了经济管理领域。CHUTIA R［3］基于区间数几何距离、高度和回转半径的概念，定义区间数相似度计算模型，将其应用于家禽养殖风险分析现实问题，取得了很好的结果。由此可见该理论被应用到了各种不同的领域，充分说明了其在不确定性环境下的应用价值。

但人们在学习和梳理以往学者们的区间数决策理论时，时常感觉到一些成果与人们的认知不全吻合。特别注意的是，所有文献中特征参数或对属性评价在区间上的取值服从均匀分布的假设过于简单化。事实上，一方面，人们对客观事物进行区间估计，目的在于提高估计的可信度，降低估计错误的风险，但并非一定认为区间中取值服从均匀分布。从统计的角度，一般也很难属于均匀分布。另一方面，即使为了简单方便而假设服从均匀分布，但是在多属性决策分析过程中，无可避免要对区间数进行加、减、乘、除甚至幂运算。而众所周知，区间数运算可理解为多个取之于区间的随机变量的运算，比如两个区间数和运算就相当于取值于对应区间且服从均匀分布的两个随机变量之和，经过“和运算”后，其取值范围虽然还是一个区间，但取值所服从的分布变成了三角型分布，并非是均匀分布。而且如果参与运算的区间数更多，其分布就更复杂，更不可能为均匀分布。因此，将区间数决策理论建立在均匀分布的假设基础上值得认真思考。为此，本文将区间上的取值分布推广到一般分布，旨在构建具有普适性的相似度计算模型，进一步完善区间数决策理论，夯实其在应用中的理论基石。

1 基本概念

定义1［1］(区间数)若 －! ＜ a－≤a+＜ +!，则称a=［a－，a+］为实数空间中的有界闭区间数。如果a－≥0，则称a=［a－，a+］为非负有界闭区间数。特别地，如果a－=a+=a，则a=［a－，a+］退化为实数 a 。

记 I {a=［a－，a+］:a－，a+∈ (－ !，+!)} ，则称之为实数空间上的有界闭区间数集合。胡启洲等［1］给出了区间数的基本运算法则。

定义 2［1］(区间数运算法则)设 a=［a－，a+］和 b=［b－，b+］是 I上的任意两个有界闭区间数，则:

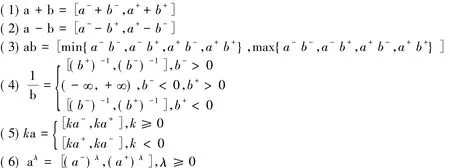
在现实决策与分析中，人们需要对区间数进行比较，分析区间数的相似性与大小关系。为此，许瑞丽等［2］提出了区间数相似的概念，但该文献并没有清晰地阐述区间数相似的内涵，不过通过分析其构建的区间数相似度计算模型，相似的内涵可用下面的定义描述。

定义3 (区间数相似事件)设a=［a－，a+］和b=［b－，b+］是I上的任意两个有界闭区间数，如果两个变量X和Y的取值区间分别为［a－，a+］和［b－，b+］，用a∩b表示两区间的交集，则区间数 a=［a－，a+］与 b=［b－，b+］的相似事件定义为 {a∩ b} {(x，y):x，y∈a∩b}。

相应地，如果两个区间的交集越大，则相似程度越高。这种相似程度也就被许瑞丽和徐泽水定义为区间数的相似度，记为Sa，b。

2 区间数相似度计算模型

基于区间数相似度的定义，许瑞丽等在默认区间上的取值服从均匀分布的前提下构建了相似度的测度模型。

定义 4［2］设 a=［a－，a+］，b=［b－，b+］，且设qj(j=1，2，3，4) 为a－，a+，b－，b+中第 j大的数，则区间数a与b之间相似度定义为

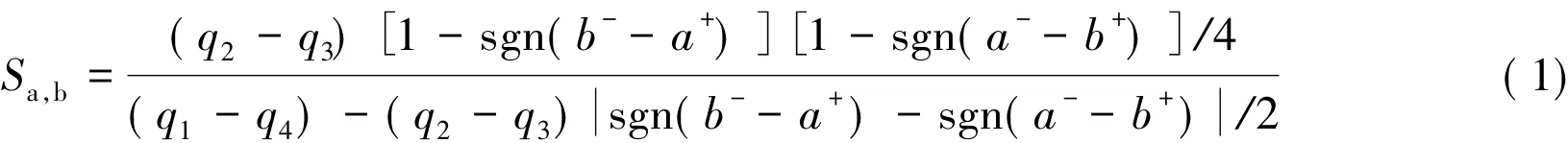
其中，sgn(x)为符号函数，如果x＞0，则sgn(x)=1;如果x=0，则sgn(x)=0;如果x＜0，则sgn(x)=－1。将(1)式分解，也就是

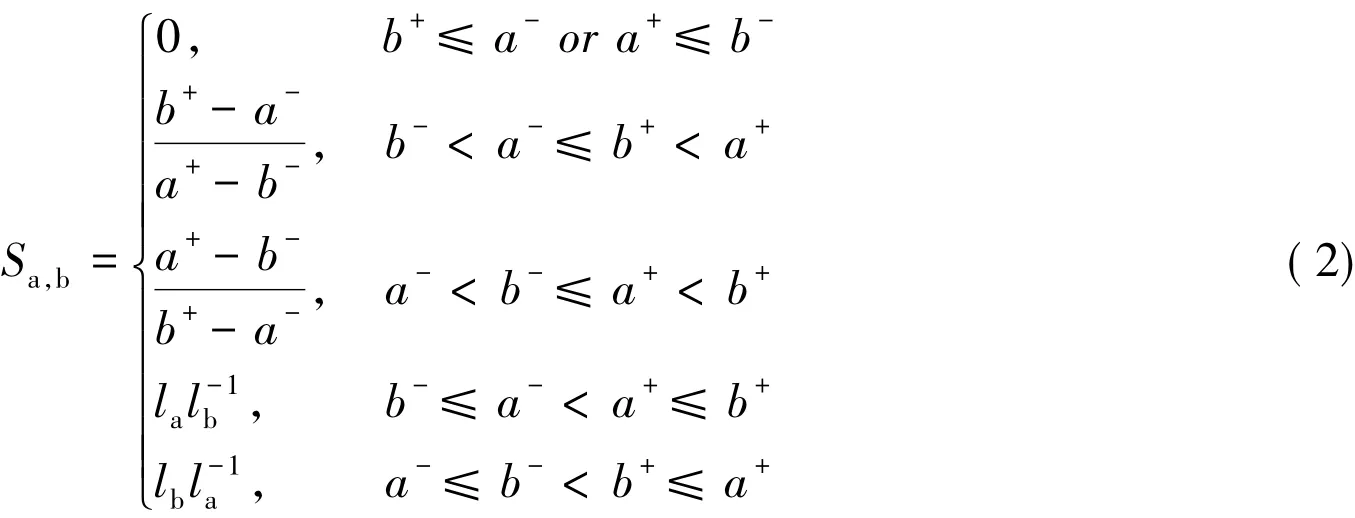
其中 la=a+－ a－，lb=b+－ b－。

对于上述模型，许瑞丽等［2］给出了如下基本性质。

对于给定的区间数 a=［a－，a+］，b=［b－，b+］，c=［c－，c+］，相似度具有如下性质:

1)有界性:0≤Sa，b≤1，其中，Sa，b=1，当且仅当 a=b，即 a+=b+，a－=b－，此时称a 和 b完全相似;Sa，b=0当且仅当a+≤b－或b+≤a－，此时称a和b完全不相似。

2)对称性:Sa，b=Sb，a。

3)传递性:如果a和b完全相似，b和c完全相似，则a和c完全相似。

以上定义和性质建立在区间上的取值服从均匀分布的假设基础之上，但是发现人们用区间来估计客观事物属性指标的取值，在取值区间上不一定服从均匀分布。如不同企业的员工工资在最小值和最大值区间范围内，员工工资就不服从均匀分布，而且不同企业的工资分布还不相同。理论上，即使为了将复杂问题简单化，假设区间［a－，a+］和［b－，b+］上取值服从均匀分布，但在基于区间数进行决策的过程中，不可避免地要根据定义2对区间数进行运算，如和运算a+b=［a－+b－，a++b+］，显然其相当于两个相互独立且服从均匀分布的随机变量之和构成的取值区间。根据概率论知识，其分布已经变为一个三角型分布，而不再是均匀分布。因此，在实际决策过程中，区间数经过运算后，仍然默认其服从均匀分布是不严谨的。为此，文中将均匀分布推广到一般分布，希望能构建更合理、更科学的相似度计算模型，为区间数决策理论夯实基石。

根据定义3，假设X和Y相互独立，且分别取值于区间［a－，a+］和［b－，b+］，分布函数分别为F(x)和G(y)，对应的密度函数为f(x)和g(y)。根据概率论基本理论，二维随机向量(X，Y)的联合分布密度函数w(x，y)=f(x)g(y)。于是，两个区间数相似度可定义为X和Y独立地取值于的交集的概率。用条件概率的公式刻画，也就是

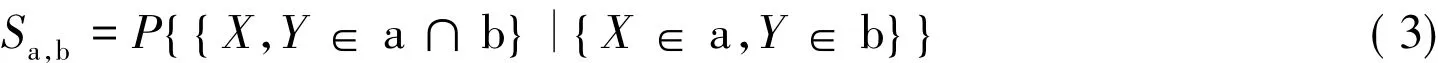
根据两个区间数在数轴上的6种位置关系，转化为两个随机变量X和Y在平面上的取值区域关系(见图1)。(X，Y)的取值区域为区间［a－，a+］和［b－，b+］构成的一个矩形，区间数相似的事件也就可直观地理解为矩形中以直线y=x为对角线的一个正方形区域，记为D+，即图1中(b)～(e)子图中的阴影部分。特别地，子图(a)和(f)不存在正方形区域，表示这两类区间数不存在相似。文中定义的相似度等价于阴影部分正方形“面积”占取值矩形区域“面积”的比值。由于X和Y独立地取值，分别服从分布F(x)和G(y)，因此，相似度可以定义为

对此，根据图1中(a)～(f)等6类区间数位置关系，分别计算其相似度，可得到其具体计算模型:

1)图1(a)和(f)的情形，即b+≤a－或a+≤b－，此时事件{a∩b}=φ，显然相似度Sa，b=0。

2)图 1(b)的情形，即 b－＜ a－≤ b+＜ a+，此时有

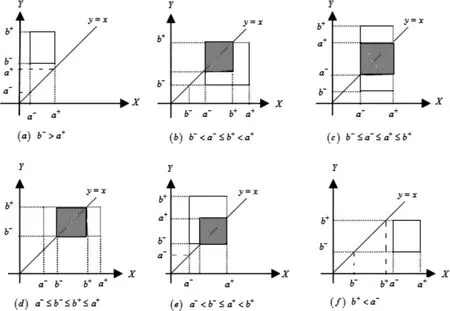
图1 区间数相似平面示意图Fig．1 Schematic diagram of interval number similarity

3)图 1(c)的情形，即 b－≤ a－＜ a+≤ b+，同理有

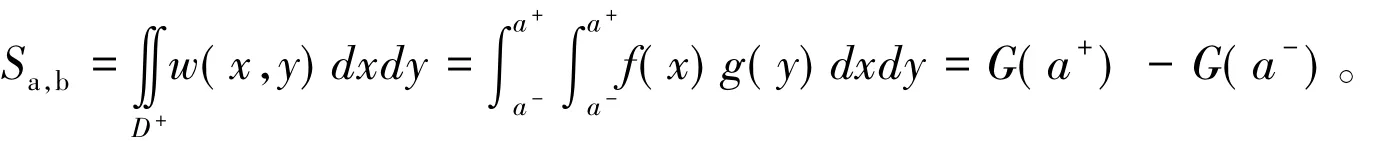
4)图 1(d)的情形，即 a－≤ b－＜ b+≤ a+，有

5)图 1(e)的情形，即 a－＜ b－≤ a+＜ b+，此时有

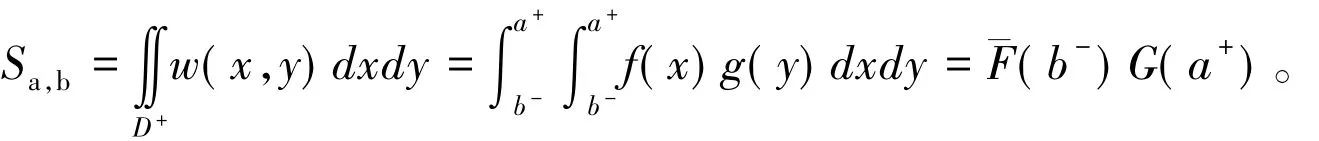
定义 5 设 a=［a－，a+］和 b=［b－，b+］是 I上的任意两个有界闭区间数，区间［a－，a+］和［b－，b+］上的取值分布函数分别为 F(x) 和 G(x)，则相似度 Sa，b计算模型为

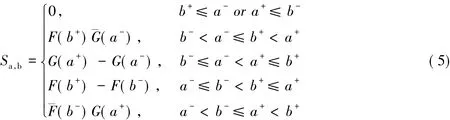
特别地，当 X 和Y 取值分别服从均匀分布F(x)=U［a－，a+］和G(x)=U［b－，b+］时，即

相似度Sa，b计算模型为

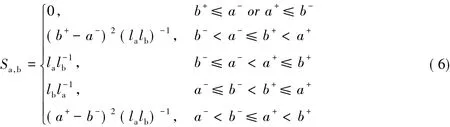
显然(6)式与许瑞丽和徐泽水(2007)给出的(2)式在b－＜a－≤b+＜a+和a－＜b－≤a+＜b+两情形下存在差异。但是，不难证明它们是等价的。对此，只需在b－＜a－≤b+＜a+下，证明(6)式与(2)式的计算公式有如下不等式

恒成立，至于在a－＜b－≤a+＜b+的条件下是完全雷同的。事实上，在b－＜a－≤b+＜a+下，对于不等式(7)式，当a－＜b+时，显然有:

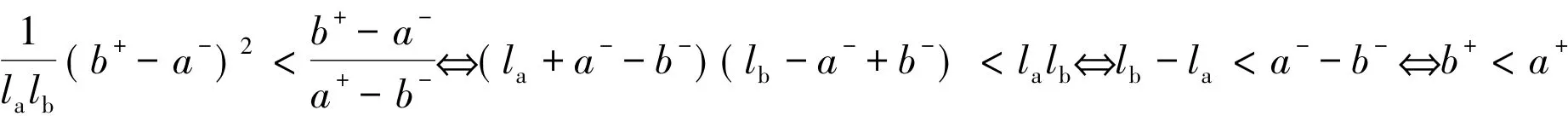
成立;显然a－=b+，则(7)式等号成立。充分说明定义6和定义4是等价的。

此外，同样很容易证明定义5所给出的相似度计算模型同样满足文献［2］中的性质。但不难发现，要运用定义5计算区间数的相似度，首先必须明确每个区间上的取值分布。可在现实中，如果要一个个的将每个具体属性指标的实际取值分布找出来，并且使用这些分布去计算求得具体事物的总体特征值分布是不现实的。必须通过简化，使问题能够采用统一而又相对简单的办法进行分析。对此，英国STEPHEN GREY等研究发现，人们最能够接受的方法是将所有分布统一简化成三角型分布，因为通过三角型分布，可估计最大、最小及最可能的值(众数)及相应的概率，特别是当属性指标比较多的情况下，采取三角型分布去简化复杂的真实分布，所损失的信息量较小，而且由此所得到的结果与真实情况相差不大，应用也方便。为此，下面给出在三角型分布假设下的相似度计算模型。

一般地，取值于任意区间［a－，a+］上的三角型分布具有如下的分布函数式:

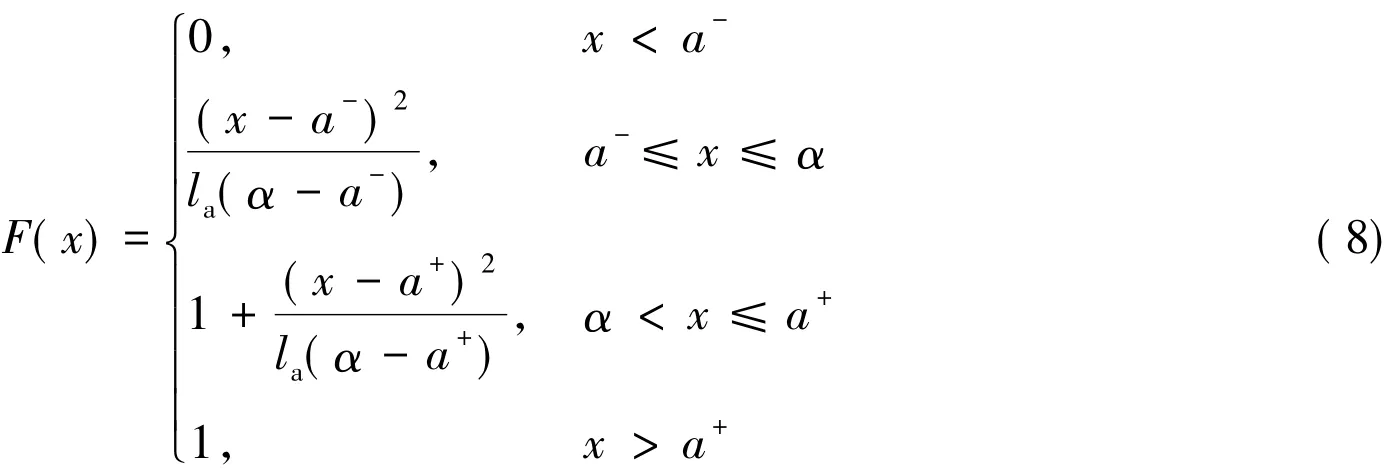
其中a－≤ α≤ a+，α表示众数，其在区间［a－，a+］上的位置决定着分布偏态。如果α ＞(a－+a+)/2，则分布是右偏;如果 α ＜ (a－+a+)/2，则分布是左偏;如果 α=(a－+a+)/2，则分布是对称分布。为了表述的方便，区间［a－，a+］上的三角型分布记为Δ［a－，α，a+］或 a ～ Δ［a－，α，a+］。

对于区间数 a和 b，假设 a ～ Δ［a－，α，a+］，b ～ Δ［b－，β，b+］，分布函数分别为 F(x)和G(x)。根据众数的位置关系，即分布的偏态程度，以b－＜a－≤b+＜a+情形为例，可以分解为如下5种类型，见图2。

于是针对图2中的五种类型，根据定义5很容易就计算得到b－＜a－≤b+＜a+情形下的区间数相似度的计算公式:

图2 两个区间数的分布关系示意图Fig．2 Schematic diagram of the distribution of two interval numbers

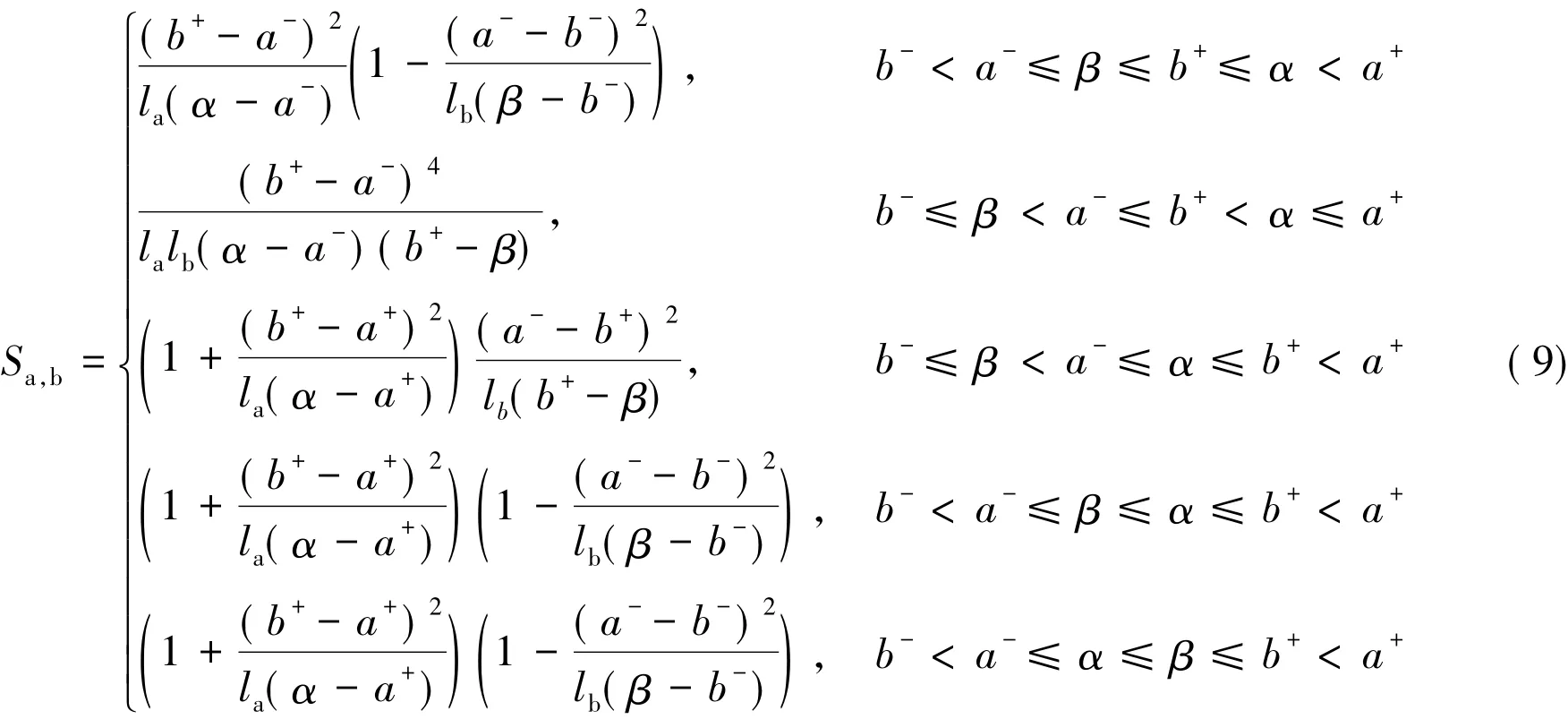
完全类似地，可以获得定义5中其他类型在三角型分布下的具体计算公式，由于版面限制问题，文中不一一写出。下面在a－＜b－≤a+＜b+的条件下，以区间数a=［3，11］和b=［0，8］为例，分4类不同三角型分布(见图3)以及同时服从均匀分布的两种情形下，计算区间数相似度，借以说明定义5的合理性。

在服从不同三角型分布(各个具体的分布见表1)，以及同时服从均匀分布的两种情形下，分别根据式(6)和式(9)，区间数相似度的计算结果如表1。

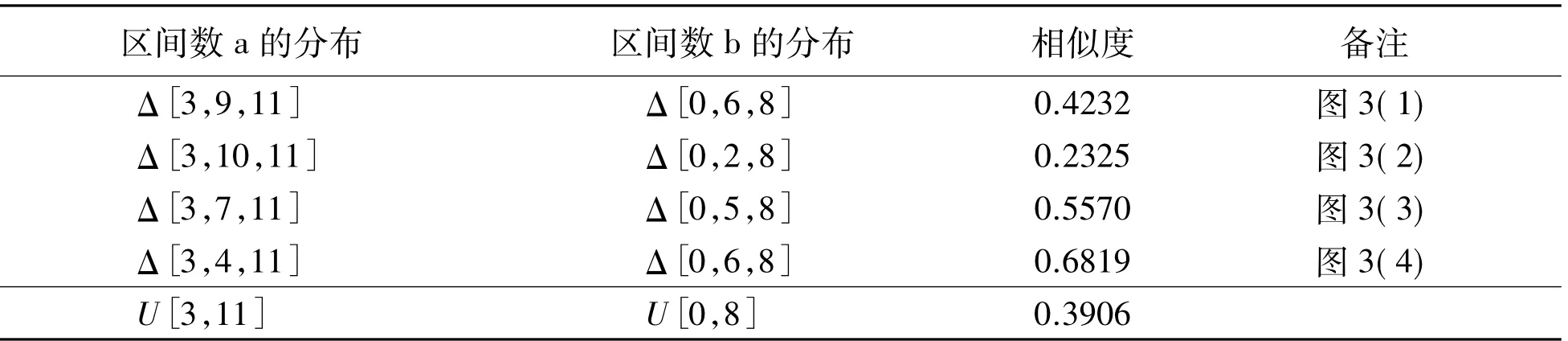
表1 区间数［3，11］和［0，8］在不同分布下的相似度计算结果Table 1 Results of similarity calculation for interval numbers［3，11］and［0，8］under different distributions

从表1的计算结果可以看出，对于给定的两个区间数，它们的交集是完全一样的，均为

图3 区间数［3，11］和［0，8］在不同三角分布下的相似度示意图Fig.3 Schematic diagram of the similarity of interval numbers［3，11］and［0，8］under different triangular distributions

［3，8］，但是当属性特征的取值服从的分布不同时，区间数的相似度是不一样的。三角型分布能比较细腻地刻画决策者的风险态度，能将分布的偏态、峰度、众数的概率等信息的差异性较好地呈现出来，显然丢失的决策信息要比简单的均匀分布少很多。如对于图3中(2)的情形，如果把两个区间数看成是两个不同风险类型的决策者对某个事物给出的评价值，则直观上就可以看出，他们的取值落在相同区间［3，8］的概率肯定很小，计算结果也显示小于均匀分布假设下的相似度。而对于图3中(4)的情形，显然取值落在相同区间［3，8］的概率肯定较大，计算结果正好验证了这一直观。由此说明文中研究一般分布假设下的区间相似度计算模型，并以三角型分布去近似替代比较复杂的分布，构建三角型分布假设下的相似度计算模型，是非常有价值的，能为决策分析提供更准确的决策信息。

3 相似度在多属性决策中的应用

3．1 多属性决策问题描述

在管理科学与管理工程中，多属性决策是一个非常普遍的问题。对于这类问题，人们习惯于在确定性分析框架下用精确的数值刻画属性指标的特征值。但现实中，由于事物的复杂性和人们对事物认知的模糊性，往往难以获得精准的数值，只能采用一些模糊数，比如用区间数、模糊语言等去描述客观事物的评价指标。文中考虑属性指标取值为区间数的多属性决策问题，假设有n个被决策单元，记为Ai，i=1，2，…，n。决策者根据m个属性指标Ci，i=1，2，…，m;权重为 ωi，i=1，2，…，m 。对每个决策单元进行综合评价，从中确定最优决策单元。假设决策者对每个属性的评价采取区间数的形式给出，得到原始评价矩阵，记为

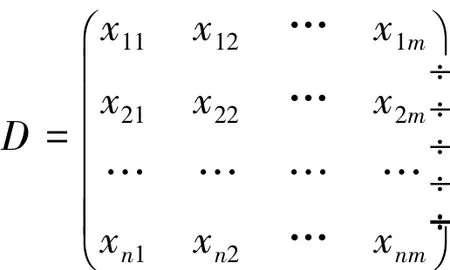
其中xij=。表示第 i个被决策单元关于第 j个属性指标的评价值。

为简单起见，假设对于每个区间数，属性指标在区间内的取值服从三角型分布，即

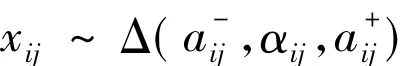
3．2 基于TOPSIS方法的多属性决策过程

根据上述区间数相似度的理论，不难发现利用区间数的相似度是不能直接对区间数的大小进行排序的。但是，如果将其应用于TOPSIS决策过程，则可以获得很好的应用价值。于是，本文基于上述问题和假设，给出如下多属性决策过程。

第一步:针对每个属性指标，决策者独立地对每一个决策单元给出区间数评价值，构建评价矩阵D。

第二步:标准化评价矩阵。将区间数xij进行标准化的处理，使得每个属性的取值变为正向，即区间数越大，则决策单元的评价值越高。本文采用樊治平等［27］比重变换法标准化评价矩阵，具体变换公式为

1)当指标为效益型属性时，采用公式:

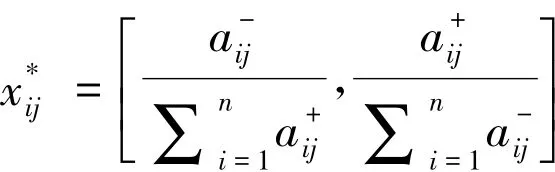
2)当指标为成本型属性时，采用公式:

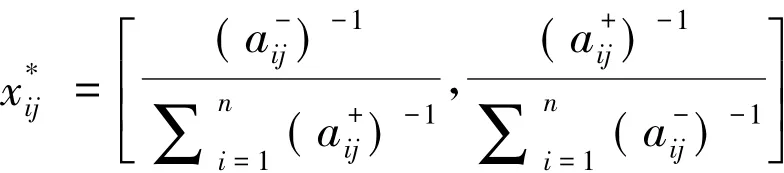
第三步:根据评价矩阵D，利用TOPSIS方法确定正、负理想解。本文正、负理想解分别记为

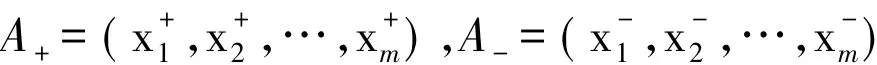
其中，xj+和xj－分别表示第j个属性指标取值的相对最理想区间数和最劣区间数，即

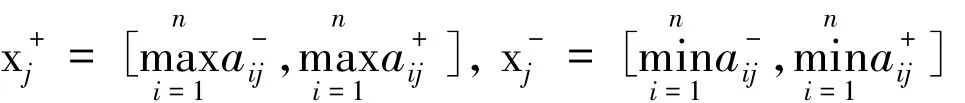
第四步:利用区间数相似度计算模型，分别计算出与正、负理想解的相似度矩阵

其中Sxj+，xij和Sxj－，xij分别表示被决策单元Ai的第j个属性取值区间数与正理想解和负理想解的第j个属性取值区间数的相似度。显然，如果Sxj+，xij越大，同时Sxj－，xij越小，则被决策单元Ai的第j个属性取值越接近正理想解。

第五步:根据相似度矩阵S+和S－，计算综合择优决策矩阵R=(rij)n×m，其中

规定(10)式中0/(0+0)=0。如果rij越接近1，则说明被决策单元Ai的第j个属性取值越接近正理想解。

第六步:根据综合择优决策矩阵R，计算每个被决策单元Ai的综合得分数，计算公式为

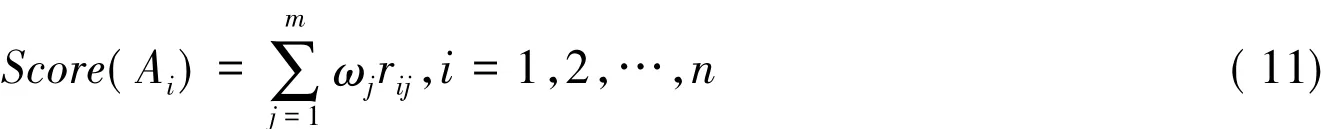
其中 ωi，i=1，2，…，m 为属性 Ci，i=1，2，…，m 的权重。

第七步:根据决策单元的得分数，选择得分最大者为最优决策单元。

值得注意的是，如果决策过程需要对每个被决策单元进行排序，而且出现了得分相等的情形，可以对得分相等的几个被决策单元重复上述第三步到第七步的决策分析过程，即可以获得全排序。

3．3 应用实例

本文选取孟志华［23］对5个企业运营绩效进行评价的实例，分别从企业的财务管理能力(C1)、经营能力(C2)、风险控制能力(C3)、发展能力(C4)和环保参与能力(C5)等五个属性指标对它们进行评价，因本文侧重点不同，直接采用孟志华［23］中利用熵值法计算得到的指标权重 ω =(0．2239，0．3309，0．2139，0．1211，0．1102)。5 个企业 5 个指标的区间数评价矩阵为

显然，正、负正理想解分别为:

根据区间数相似度计算模型，计算被决策单元分别与正、负理想解的相似度矩阵，本文假设每一个被决策单元的每一个属性在评价区间内的取值服从三角型分布，即对任意的区间数有:

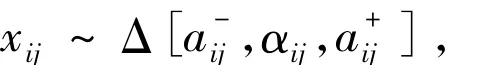
其中，αij=+λ(－)，本文取λ=0．6。在该假设下，被决策单元分别与正、负理想解的相似度矩阵分别为

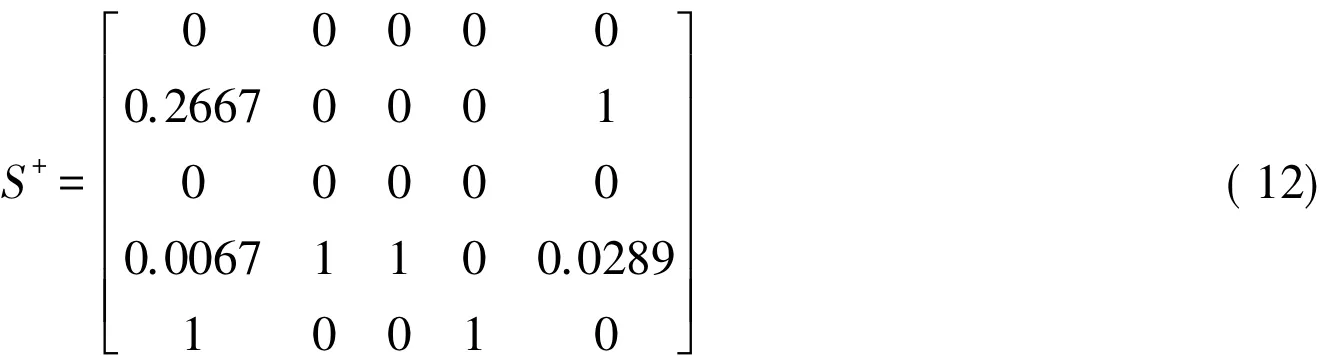
于是，根据(12)式和(13)式得到综合择优决策矩阵

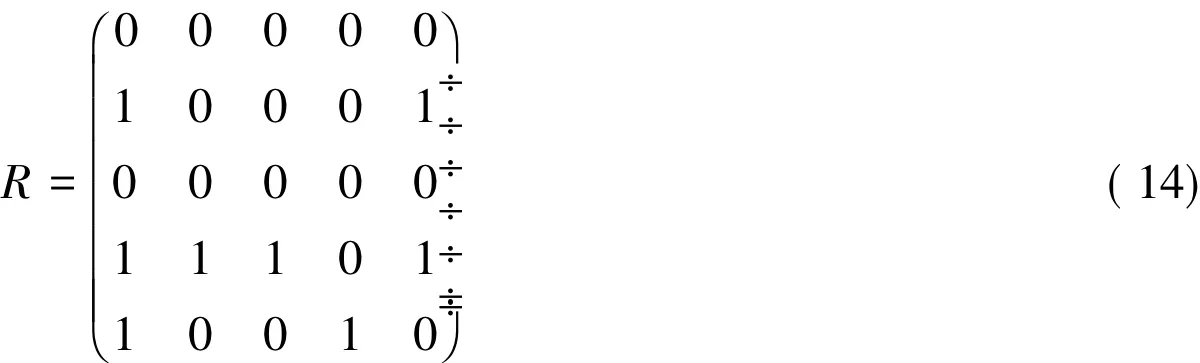
根据综合择优决策矩阵(14)式，利用公式(11)得到每个被决策单元的得分值:

Score(A4)=0．8789，Score(A5)=0．3450，Score(A2)=0．3341，Score(A1)=Score(A3)=0。其中，被决策单元A1和A3的得分值均为0。但从与负理想解的相似矩阵可以看出A3与负理想解有两个指标C1和C5完全相似，而A1却只有一个指标C2完全相似，而且C1和C5两指标的权重之和为0．3341，大于C2指标权重0．3309，所以直观上可看出A3劣于A1。于是，可以得到5个企业的绩效的排序为

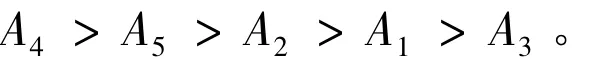
值得一提的是，孟志华［23］中存在两个方面的错误，一是加权后的评价信息矩阵的数字计算错误，二是利用TOPSIS法的决策计算过程错误。将5个企业和5个属性指标混淆了，因此其评价结果自然是错误的。不过其文章的分析思路是正确的，也并不影响文章的科学性和学术应用价值。

4 结束语

在工程和管理评价与决策过程中，用区间数刻画事物的定量属性特征大小是一种符合统计学原理和人们认知模糊性的有效方法，其描述了事物属性特征值的取值范围。从统计学的角度，客观事物的属性特征在取值范围内通常服从某一统计分布，这种分布蕴含着评价者或评价群体的偏好和风险态度，也蕴含着客观事物的不确定性。但由于事物的复杂性和人们认知的模糊性，在现实评价与决策过程中要给出或计算出这一准确的统计分布又是非常困难的，甚至是不可能的。基于这一困难，以往学者化繁为简的假设这一分布为均匀分布。然而，发现均匀分布丢失的信息太多，与统计分布信息的偏差很大，丢失了分布的偏度和峰度等能呈现评价者风险偏好的信息。为了解决这一不足，根据英国Stephen Grey等人的研究发现，采取人们最能够接受的方法，也就是将所有分布统一简化成三角型分布。因为通过三角型分布，可估计最大值、最小值、众数及相应的概率，可近似地刻画分布的偏度和峰度。这种简化，所损失的信息量也较小，由此所得到的结果与真实情况相差不大，应用也方便。

基于上述背景，本文研究了区间数相似度的计算模型，将事物属性特征值的取值看做是取值区间上的随机变量，定义两个区间数相似度为两个对应的随机变量独立取值于两个区间交集的概率。在这一概念的基础上，首先构建了它们分别服从任意分布的条件下的区间数相似度计算模型，这是一个普适性的计算模型，推广了以往学者的研究成果。然后，为了简化而又最大可能地保留人们的评价与决策信息，构建了分布为三角型分布条件下的区间数相似度计算模型。通过实例计算，充分验证了模型的可计算性，并呈现了三角型分布下区间数相似度计算模型刻画评价者或评价群体的偏好和风险态度的优良性。最后，根据区间数相似性的科学价值和应用价值，将区间数相似度理论与多属性决策TOPSIS方法相结合，构建了基于区间数相似度的多属性评价与决策模型，通过被决策单元与正、负理想解的每个属性的取值区间数相似度，建立综合评价矩阵，很好地实现被决策单元的优劣排序。显然，这一方法将在工程与管理评价决策中具有较好的应用价值。