Shibor对大中小盘股收益率影响的实证研究

李应求，韦春花，宁馨

(长沙理工大学数学与统计学院，湖南长沙，410114)

进入20世纪70年代之后，股票市场步入了迅速发展阶段，它为非资本的货币向资本转化提供了必要条件。但股票市场的大幅波动也极易对实体经济造成重大伤害，这就为各国中央银行货币政策的制定与运作带来了严峻挑战。利率作为货币政策的两大工具之一，在调控经济活动中起着至关重要的作用。因此，利率与股票市场的关系成为了金融经济学研究最核心、最前沿的问题之一。

从理论角度对利率与股票价格之间的关系进行研究始于 BLANCHARD［1］，他在FULLER［2］提出的利率和股价之间互相影响的基础上，考察了证券市场、产量与利率期限结构三者之间的相互影响关系。FAMA［3］通过对1953年至1987年间美国证券市场收益率、利率与工业生产之间关系的研究，得出证券价格与工业产量、长短期利率相关联的结论。但是SPIRO等［4］利用相同方法对更长时间段的数据进行研究之后，结果并未发现利率与股价之间存在明显的关系，可见对于所用的数据和时限不同，采用该方法所得的结论也不同。BERNANKE等［5］对联邦基金利率进行定量分析，发现市场已预期到的联邦利率变动，证券市场对其几乎不会作出反应，而未预期到的联邦基金利率的下调变动，会引起主要股价指数的上升。

我国股票市场起步较晚，实证检验层面的研究分析相对缺乏，大多停留在理论分析层面。贾永言［6］对利率、股票价格和汇率之间的关系进行了理论研究，认为利率通过市盈率对股价产生影响，在供需关系因素的影响下，股价和利率的走向可以发生偏差，但该研究结论具有一定的局限性和实效性。王军波等［7］选取了两年的日数据，利用GARCH模型及其各种推广形式对当时中国货币市场银行间同业拆借利率、证券成交量和证券日报酬率之间的关系进行了研究。结果发现货币和证券市场存在着关联性，并且沪、深两个证券市场受到利率变动带来的作用大小是不相同的，相比之下，对深市影响更大。陈德伟［8］依据向量自回归(VAR)模型对股票价格与利率之间的关系进行格兰杰因果关系检验以及方差分解，结果表明利率是股票价格的格兰杰原因。史芳芳等［9］采用GARCH扩展模型研究人民币汇率与中国股市之间的溢出效应，结果表明两者之间存在显著的溢出效应，并且存在汇率向股市的单向波动效应，见文献［10－13］。

为研究货币市场与股票市场之间的相互影响关系，本文在单变量广义自回归条件异方差(single－variate GARCH)模型基础上，扩展出多元 GARCH(multi－variate GARCH，MGARCH)模型，得以量化多个变量之间的条件波动性的溢出效应。同时将一直以来被忽略的股市休市而Shibor正常交易的情形加入VAR－MGARCH－BEKK模型，更准确地刻画货币市场和股票市场的联动关系。

1 数据来源及统计特征

1．1 数据来源

本文采用Shibor(上海银行间同业拆放利率)7天加权利率作为价格型货币政策的指标，Shibor是我国央行希望培育的中国货币市场的基准利率体系，于2007年1月4日正式运行，因此本文选取时段为2007年1月4日到2017年12月29日的日数据;同时选用沪深300指数和中证500指数分别代表大中盘股和小盘股。对于股市休市而Shibor正常报价的数据不进行剔除，总共获得2748组观测值，数据来源于wind数据库和中国货币网。

本文将每日股价的收益率ri，t定义为当日收盘价对数的差分乘100，即:

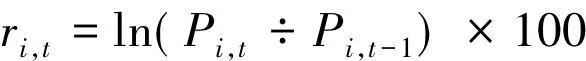
其中，Pi，t表示第i个指标在第t日的收盘价;ri，t表示第i个指标在第t日的收益率;i=1代表沪深300指数;i=2代表中证500指数;i=3代表Shibor。

1．2 统计特征分析

对沪深300、中证500和Shibor收益率进行统计描述性分析如表1，从表1可知Shibor收益率的均值为0．02。中证500指数收益率的均值为0．03，大于沪深300指数收益的均值0．01。从标准差角度分析，Shibor、中证 500 和沪深 300 收益率分别为 9．089、2．119、1．842，表明相较于股票市场，货币市场的波动性更为剧烈，而小盘股的波动性大于大中盘股的波动性。JB统计量显示在1%的显著性水平下，三个序列均拒绝正态分布的零假设，因此说明沪深300指数、中证500指数、Shibor的收益率序列都是非正态分布。而偏度都是负值，峰度均大于3，说明沪深300、中证500和Shibor收益率的分布均具有尖峰厚尾且左偏的特征。

表1 三个指标收益率的描述性分析表Table 1 The descriptive analysis table of returns rate for three indicators

为避免“伪回归”现象，采用ADF检验对数据进行平稳性检验，沪深300指数、中证500指数、Shibor收益率的检验结果见表2(其中检验形式的c、t、k分别表示常数项、趋势项、最优滞后阶数)。从表上可知三者的ADF统计量在1%的显著性水平下均拒绝了原假设，说明它们都是平稳序列，可以采用多元GARCH方法进行建模。

表2 三个指标收益率ADF检验结果表Table 2 The ADF test results of returns rate for three indicators

对数据进行自相关性检验，结果如表3所示，从表3可知沪深300指数收益率序列在5%的水平下拒绝原假设，说明该收益率序列存在自相关，而中证500指数收益率序列和Shibor收益率序列都在1%的水平下显著地存在自相关，这也就说明了沪深300指数、中证500指数、Shibor的收益率序列都存在着明显的ARCH效应。

表3 自相关检验结果表Table 3 The autocorrelation test results rate table

表4为沪深300指数、中证500指数收益率与Shibor收益率的非条件相关性检验结果，可知其非条件相关系数均约为－0．04，这与利率和股票价格呈负相关的理论是一致的，由于相关系数都较低，说明相关性不显著。作为一种静态的相关系数，非条件相关系数并未考虑到相关性随时间动态的变化，因此接下采用的改进VAR－MGARCH－BEKK模型对相关性进行分析。

表4 Shibor与沪深300、中证500收益率的相关系数表Table 4 The relevance coefficient table of Shibor with CSI 300 index and CSI 500 index returns rate

2 模型介绍

2．1 VAR－MGARCH－BEKK 模型

VAR－MGARCH－BEKK模型是将多元GARCH模型建立在向量自回归的基础上实现的，首先应用p阶向量自回归VAR(p)作为均值方程，

其中，Yt为当期变量向量;Yt－i为Yt的滞后i期变量向量;εt为随机误差向量。服从如下分布:

其中It－1是t－1时刻的信息集;Ht为对应的协方差矩阵。对于p=2的二元VAR模型，VAR(2)模型可以展开如下矩阵形式:

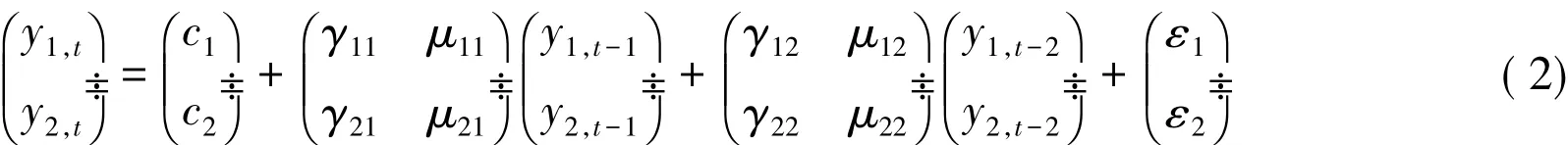
ENGEL等［13］提出的GARCH－BEKK模型，保证了在较少的约束条件下既允许不同市场间的条件方差和协方差相互影响，又保留变量间协方差矩阵的正定性，这就为分析金融市场间的时变联动性提供了有力的支持。以BEKK形式表示的多元GARCH模型的方差方程如下:

其中，C为常数项的上三角矩阵;A为ARCH项的系数矩阵;B为GARCH项的系数矩阵。那么二元MGARCH－BEKK(1，1)模型展开如下:

2．2 改进的VAR－MGARCH－BEKK模型

目前国内在研究货币市场对股票市场的影响关系时，在数据的选取上往往是对两者之中存在的任何一个无效数据进行删除，保存两个市场当天同时有效的数据。因此本文考虑到股市休市而Shibor正常报价的“节日效应”，从而使得研究结果与实际事实的更加相符。综合AIC、SC、HR信息准则、LR统计量和FPE五个评价准则的结果，选取VAR(3)为均值方程，在国内现有研究的基础上，将股市休市而Shibor正常报价的“节日效应”加入到VAR(3)模型当中，得到改进后的VAR－MGARCH－BEKK模型。

首先给出关于沪深300、中证500和Shibor收益率的改进的二元条件均值方程为

其中，Rt为当期第t日收益率;Φ表示长期漂移项;A表示滞后一期指标变动对当期指标的影响的系数矩阵;B表示滞后一期指标变动对当期指标的影响的系数矩阵;C表示滞后一期指标变动对当期指标的影响的系数矩阵;Dt表示各交易日对应的虚拟变量;ωkt表示在第t日的前1～N个股市休市。但Shibor正常报价日中，相应的Shibor收益率对当期日t的股票收益率的变动影响。

其次相应的条件方差方程，即MGARCH－BEKK(1，1)模型为

其中Ht为2×1阶的条件协方差矩阵矩阵;D表示的常数项上三角矩阵;K和F分别表示2×2阶ARCH项和GARCH的系数矩阵。

3 实证分析

3．1 Shibor对沪深300指数影响的实证分析

采用改进后的VAR－MGARCH－BEKK模型对沪深300指数和Shibor收益率之间的相关性进行实证研究，本文结合了BHHH算法进行极大似然估计，采用WINRATS软件对模型进行计算，得到关于沪深300指数、Shibor收益率的VAR(3)－MGARCH(1，1)－BEKK模型的参数估计如下表5和表6。表5和表6括号内为参数对应的t统计量，“＊＊＊”、“＊＊”、“*”表示分别通过了1%、5%、10%的显著性水平检验，表6中最后两栏括号中的值为Ljung－Box Q统计量对应的概率值(下同)。

表5 Shibor与沪深300指数收益率的均值方程的参数估计结果Table 5 Parameter estimation results of the mean equation of Shibor and CSI 300 index returns rate

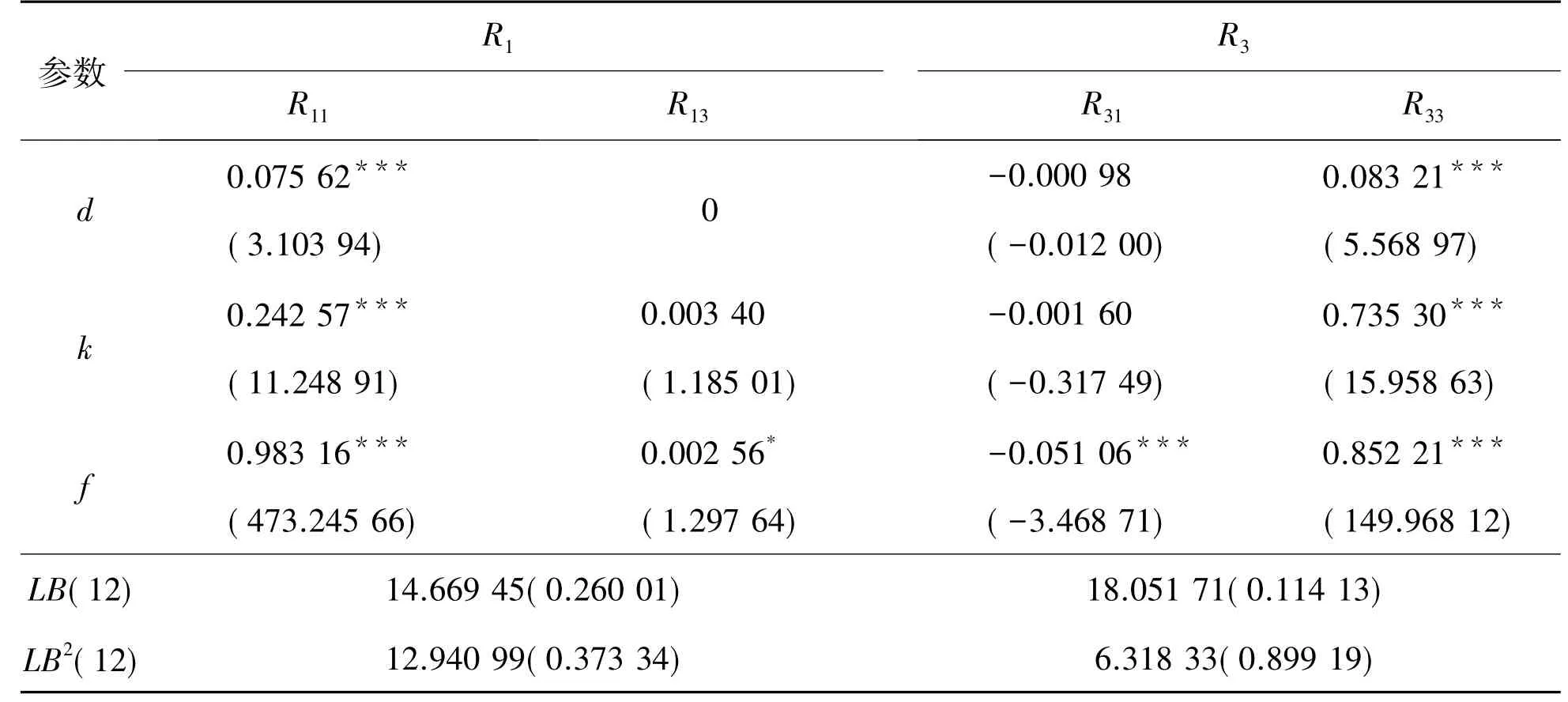
表6 Shibor与沪深300指数收益率的方差方程的参数估计结果Table 6 Parameter estimation results of variance equation of Shibor and CSI 300 index returns rate

R1、R3分别表示沪深300指数、Shibor收益率，由表6中最后两栏的残差检验结果可知，在滞后12阶的情况下，两者残差的Ljung－Box Q统计量的概率值均大于10%，可见残差中已不存在自相关。同时对残差的平方进行假设检验，结果均不能拒绝原假设，即不存在自相关的假设，因此残差之间不存在ARCH效应，序列中自相关和条件异方差的影响被消除，故所建立VAR(3)－MGARCH(1，1)－BEKK模型通过检验。接下来分析条件均值和方差方程的参数估计结果。

在均值方程的参数估计表5中，系数a11、b11、c11分别在1%、5%、10%的显著性水平下通过了检验，表明沪深300指数收益率自身存在一阶、二阶、三阶相关。Shibor收益率的自相关系数a33通过了显著性检验，而b33、c33未通过检验，说明了Shibor收益率序列一阶自相关。此外，系数b13在1%的显著性水平下显著异于零，这表明沪深300指数收益率受到Shibor收益率二阶滞后项的影响，也说明了Shibor收益率对沪深300指数收益率具有一定的信息传导效应。系数a31在10%的显著性水平下显著异于零，这表明沪深300指数收益率对Shibor收益率具有信息传导效应。

在方差方程的参数估计表6中，反映自身ARCH效应的参数k11、k33均在1%的显著性水平下显著不为零，这说明沪深300指数收益率序列和Shibor收益率存在显著的ARCH效应。反映GARCH效应的四个系数f11、f13、f31、f33表示全部通过显著性检验，拒绝为零的原假设。f11、f33分别反映沪深300指数收益率序列、Shibor收益率序列自身的GARCH效应，f13反映了Shibor收益率序列对沪深300指数收益率序列的GARCH效应，而f31反映了沪深300指数收益率序列对Shibor收益率序列的GARCH效应。f13通过了10%的显著性检验，而f31通过了1%的显著性检验，这就说明相较于沪深300指数的波动性对Shibor的持续影响，Shibor的波动对沪深300指数波动的持续影响更剧烈。

3．2 Shibor对中证500指数影响的实证分析

用上述同样的方法对中证500指数和Shibor 7天同业拆放利率对数收益率之间的相关性进行探讨，相应的VAR(3)－MGARCH(1，1)－BEKK模型的估计结果如表7和表8所示:

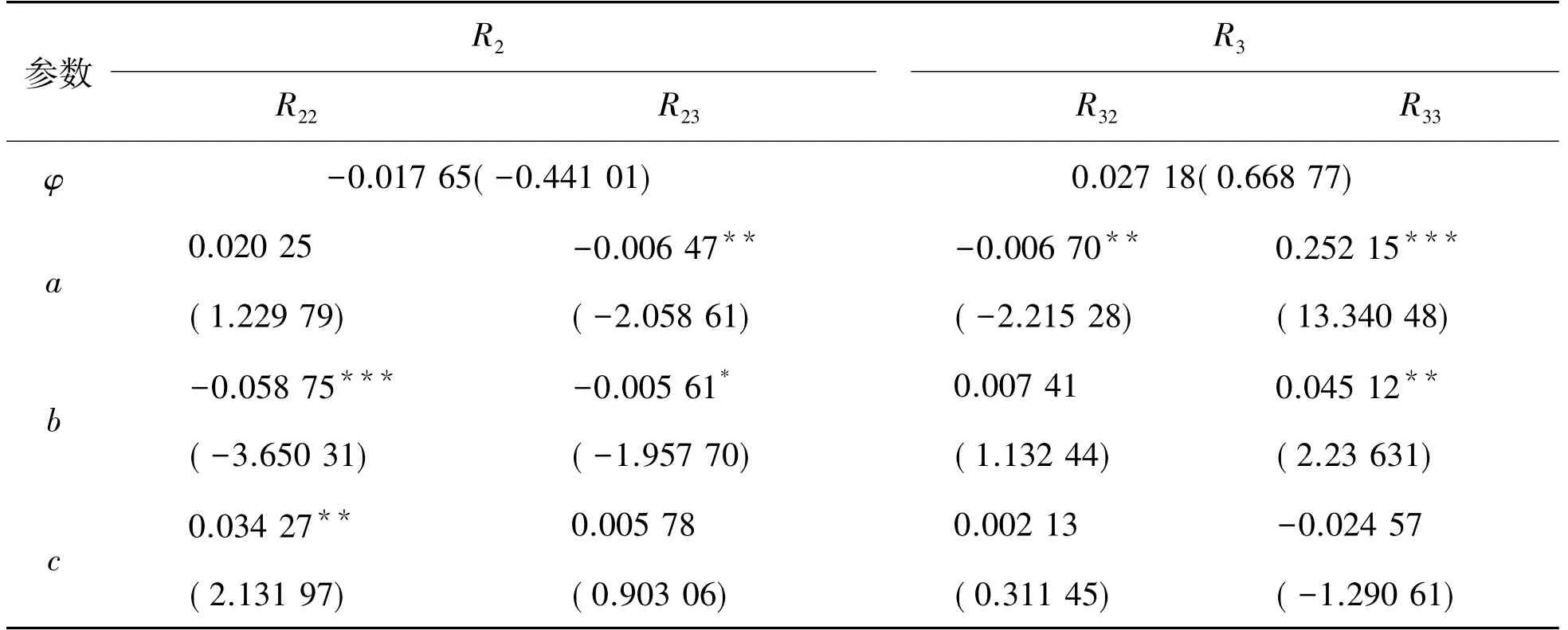
表7 Shibor与中证500指数收益率的均值方程的参数估计结果Table 7 Parameter estimation results of mean equation of Shibor and CSI 500 index returns rate

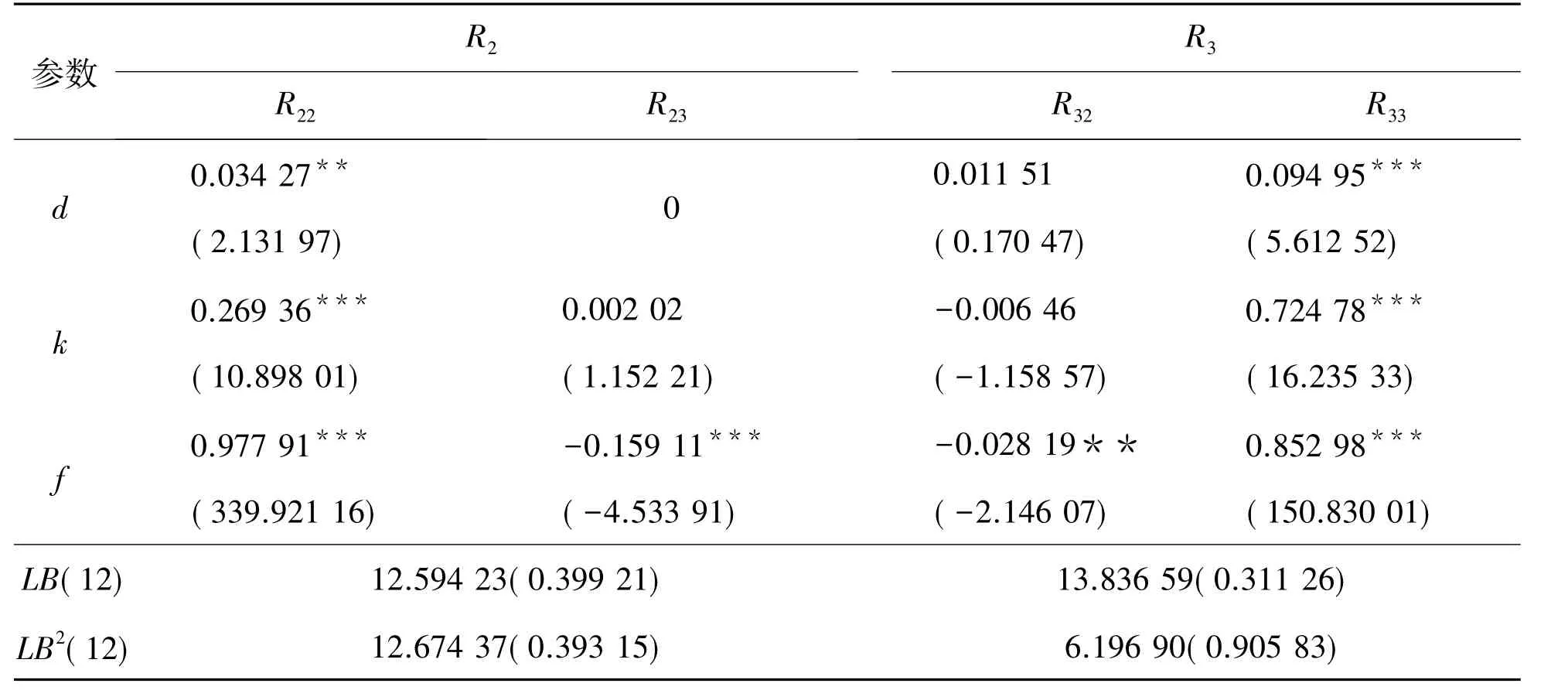
表8 Shibor与中证500指数收益率的方差方程的参数估计结果Table 8 Parameter estimation results of variance equation of Shibor and CSI 500 index returns rate

R2、R3分别表示中证500、Shibor收益率。由表8中最后两栏的残差均通过了检验，即两者残差以及残差平方均通过了滞后12阶的Ljung－Box Q统计量的检验，说明序列中自相关和条件异方差的影响被消除。因此所建立VAR(3)－MGARCH(1，1)－BEKK模型通过检验。

在均值方程的参数估计表7中，系数b22、c22分别在1%、5%的显著性水平下通过了检验，表明中证500指数收益率序列存在显著的二阶、三阶自相关。除此之外，系数a32在5%的显著性水平下显著异于零，可见Shibor收益率受到滞后二期的中证500指数收益率产生的影响。系数a23、b23分别通过了5%和10%的显著性水平检验，表明中证500指数收益率受到滞后一二期Shibor收益率序列的影响，即Shibor收益率对未来中证500指数收益率有一定的信息传导效应。

在条件方差的参数估计结果表8中，反映自身ARCH效应的参数k22、k33均在1%的显著性水平下显著不为零，这说明中证500指数收益率序列和Shibor收益率序列均存在相应的ARCH效应。反映GARCH效应的四个系数f22、f23、f32、f33表示全部通过显著性检验，拒绝为零的原假设。f22、f33分别反映了中证500指数收益率序列、Shibor收益率序列自身的GARCH效应，f23反映了Shibor收益率序列对中证500指数收益率序列的GARCH效应，而f32反映了中证500指数收益率序列对Shibor收益率序列的GARCH效应。f23、f32分别通过1%和5%的显著性水平检验，由此说明Shibor收益率序列对中证500指数收益率序列的波动具有显著影响，相较而言，Shibor收益率序列的波动对中证500指数收益率序列波动的持续影响更为显著。

4 结论与建议

由上述实证可知，滞后一期的Shibor收益率对中证500指数收益率的影响更加明显，而沪深300指数收益率更多的是受到滞后二期Shibor收益率的影响。此外，在冲击程度和持续波动上，前期的Shibor收益率对当期小盘股的影响较大盘股更为明显。因此可以通过制定相应的货币政策，从而调整股票市场的走向。在股票市场对货币市场的影响方面，前期大中盘股的持续波动对Shibor收益率的影响更加显著。说明了相较小盘股，价格型货币政策在制定时会更多地考虑到大中盘股的情况。综上，给出以下几点建议:

1)央行在制定货币时，应当充分地考虑到大中盘股和小盘股的冲击程度和持续波动的影响作用，做好对股票市场的全面监控。

2)在金融市场的资金合理配置上，应当考虑到货币市场和股票市场之间的相互流动性，加强金融风险的管理，使得金融市场的资源配置更加完善。

3)持续不断地推动利率市场化的改革，在巩固Shibor作为货币市场的基准利率的同时，加强利率市场与股票市场的联系。通过分析利率波动带来的投资风险，可以将利率作为股票市场的内生变量，对股票市场收益率的波动性做进一步预测，从而提高货币政策的调控作用。

4)对投资者而言，考虑到滞后一期的Shibor收益率对小盘股的影响更为强烈，而滞后二期的Shibor收益率对大中盘股的影响更为显著。因此在选择投资大中盘股时，会有更充足的时间来考虑Shibor的影响。而选择投资小盘股时，需要在更短的时间内考虑到Shibor对小盘股的影响。投资者在选择投资时，需要酌情考虑到Shibor收益率对大中小盘股产生相应的影响，从而避免相应的投资损失。