FPSB与连接浮桥耦合运动响应分析

晏 柳，连雪海，王小春，木建一，陈岱岱

(中电科（宁波）海洋电子研究院有限公司，浙江 宁波 315000)

0 引 言

作为一种近海浮式生产储卸平台，FPSB是岛礁建设与开发的物流基地和后勤保障，具有可移动性、受地震冲击小、对环境影响小和经济性好等优点[1]，逐渐得到广泛应用。由于FPSB需要长时间工作于海上，因而研究其主船体的运动与载荷特性对保证整个FPSB系统的运输安全作业和系泊安全具有重要意义。FPSB主船体通过浮筒桁架式栈桥与岛礁连接，浮动式栈桥既是FPSB主体与码头之间进行滚装运输的通道，也是FPSB主船体的系泊方式。目前，国内外学者针对连接浮桥的载荷响应开展了相关研究。付世晓等[2]用NEWMARK直接积分和NEWTON-RAPHSON迭代方法求解系统的非线性运动方程求解移动载荷作用下非线性连接浮桥的动力响应；PINKSTER[3]研究了移动载荷作用下静水中的系泊铰接浮体的动力响应，将浮桥简化为弹性基础梁，并通过附加质量考虑浮体周围水的动力影响，采用线性弹簧对系泊系统进行模拟。马勇等[4]应用传递矩阵方法建立了桥节、桥脚舟和连接接头的传递矩阵并组装成传递方程进行编程计算。

不同于常规的锚链连接形式，本文FPSB主船体与浮桥通过A字型钢架连接，该连接方式约束了2个浮体之间的线位移而不约束角位移，现有的计算方法并不适用于该类浮体的运动与载荷响应计算。针对这种连接结构的特点，本文提出一种求解FPSB与连接浮桥耦合运动的计算方法，建立主船体与浮桥的准静态六自由度耦合运动方程，使用自行开发的计算程序求解主船体的运动和载荷响应，分析了连接浮桥对主船体的运动和波浪载荷的影响规律，并研究了满载状态下主船体的载荷特性，为连接结构的设计与评估提供参考。

1 三维源汇分布法

三维源汇分布法是目前发展较为成熟的计算浮体运动响应和波浪载荷的方法。该方法基于三维线性频域势流理论，假设流体是不可压缩的无旋流体，并且作用于船体和浮桥上的入射波是微幅波，因而流体的运动可以用速度势描述[5]。和 t分别是相对于固定坐标系的位置矢量和时间。

根据势流理论，其空间部分可进一步分解为入射波势、绕射势和辐射势：

通过求解流域内满足边界条件的边界积分方程，可以求出速度势，进而通过伯努利方程求得一阶水动力压力分布：

通过对浮体湿表面压力积分，可以得到流体作用力。水动力可以分解成入射力和绕射力。作用力表达式为：

由于船体运动产生的辐射力为：

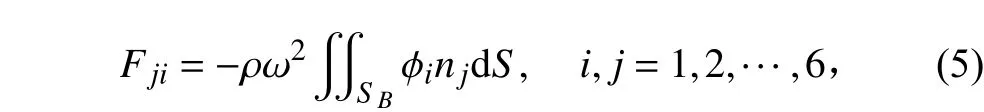
进一步分解为：

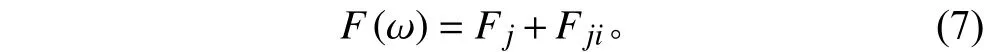
在得到规则波中浮体运动响应和脉动压力载荷后，即可应用达朗贝尔原理计算浮体剖面内的波浪诱导力和力矩，包括垂向与水平的剪力、弯矩以及扭矩[6]，进而完成浮体波浪载荷的预报。

2 FPSB 与浮桥耦合运动方程的建立

图 1 连接浮桥示意图Fig. 1 The sketch of pontoon bridge

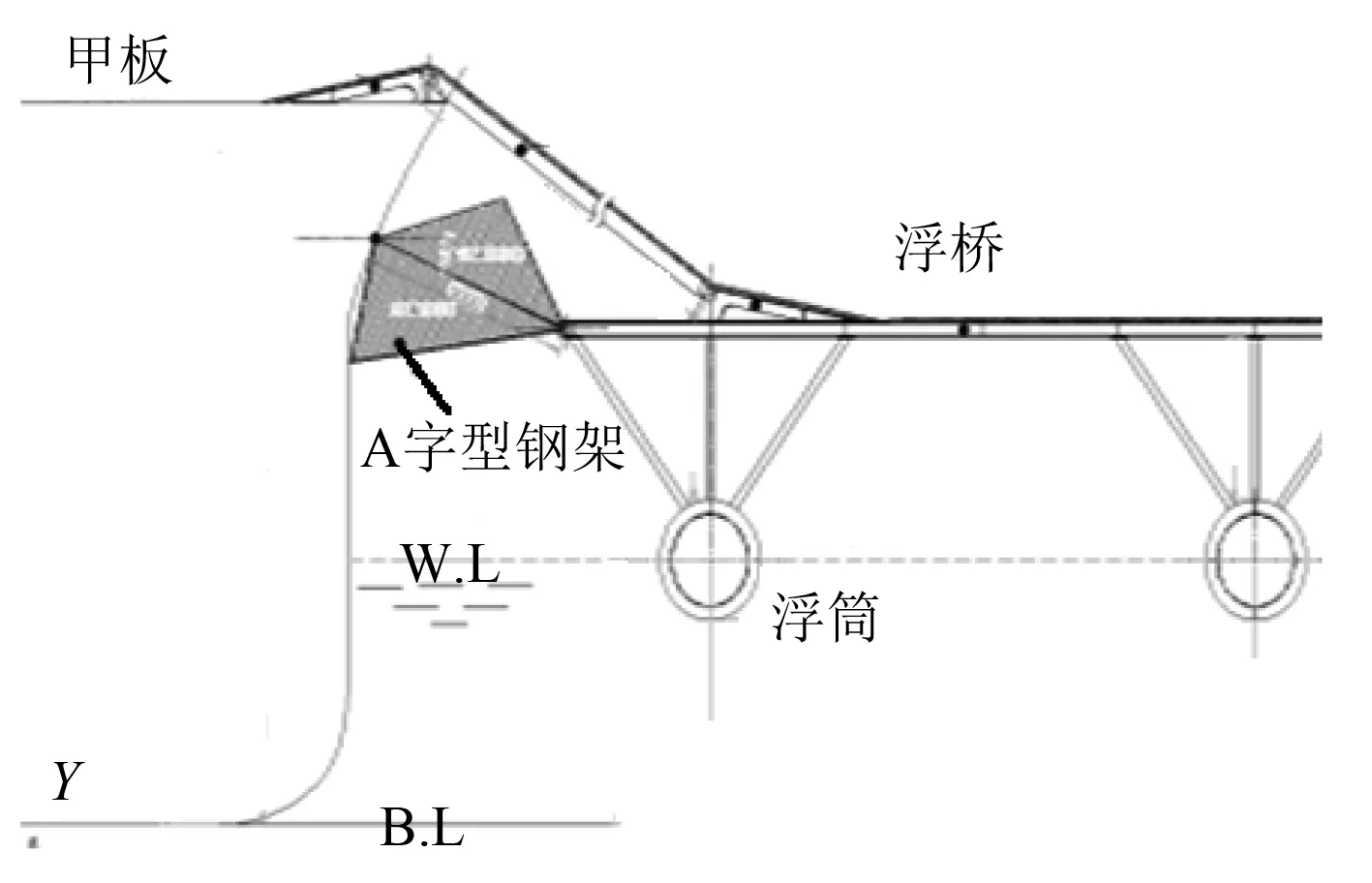
图 2 A 字型钢架示意图Fig. 2 The sketch of A type steel frame

FPSB通过浮筒桁架式浮桥与岛礁连接，如图1所示，主船体与浮桥之间采用A字型钢架连接，如图2所示。与传统的锚链连接方式不同，该连接方式约束了2个浮体之间的线位移而不约束角位移，使得钢架能够传递力而不传递弯矩，因而浮桥能够与FPSB主船体的运动保持同频率同相位，方便建立主船体和连接浮桥的耦合水动力模型。

首先采用隔离法分别建立FPSB主船体和连接浮桥的运动方程，其中FPSB主船体的运动方程为：

而连接浮桥的运动方程为：

联立式(8)、式(9)和式(10)，可得主船体与连接浮桥的六自由度耦合运动方程：

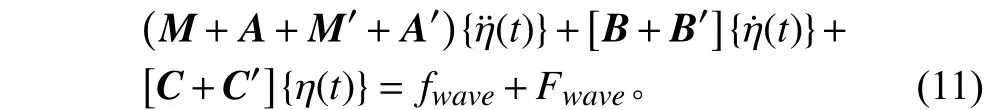
3 运动与载荷的数值计算

3.1 水动力模型的建立

在船体湿表面网格划分的过程中，为了使计算结果尽可能的精确，而又不超过程序所允许的最大网格数（10 000单元），本文在船体首尾型线变化剧烈处网格加密，并适当减少船体中部网格，分别建立FPSB主船体和连接浮桥的水动力模型，FPSB与连接浮桥的单元模块的主要设计参数如表1所示。

FPSB主船体和连接浮桥的水动力模型分别如图3和图4所示。

3.2 运动响应分析

基于FPSB主船体与连接浮桥的受力分析和耦合运动分析，确定质量系数矩阵、阻尼系数矩阵和静水恢复力系数矩阵后求解耦合运动方程，可以计算出若干个单位波幅规则波中船体的六自由度运动幅频响应值（简称运动幅值）。考虑到船体的对称性，规则波取在=0°（随浪）到=180°（迎浪），每隔30°一个浪向；对每一个浪向角，波长船长比从到之间取19个规则入射波。选择运动响应达到最大时的浪向下的响应进行结果对比分析，图5～图10给出了主船体满载状态下考虑浮桥影响之前（图中简称“方案1”）和考虑浮桥影响之后（图中简称“方案2”）FPSB主船体的六自由度运动幅值对比结果。

表 1 FPSB和浮桥主要设计参数Tab. 1 Main characteristic parameters of the FPSB and pontoon bridge

图 3 FPSB 水动力模型Fig. 3 The hydrodynamic model of FPSB

图 4 浮筒水动力模型Fig. 4 The hydrodynamic model of the buoy

表2给出了FPSB主船体满载工况下考虑浮桥影响前后的船体运动幅值的最大值对比结果，以及运动幅值达到最大时所对应的浪向和波长船长比。

从图5～图10中运动幅值对比曲线可以看出，连接浮桥的存在并未改变船体运动幅值随波长船长比变化的趋势，而仅仅改变了船体六自由度运动的幅值。

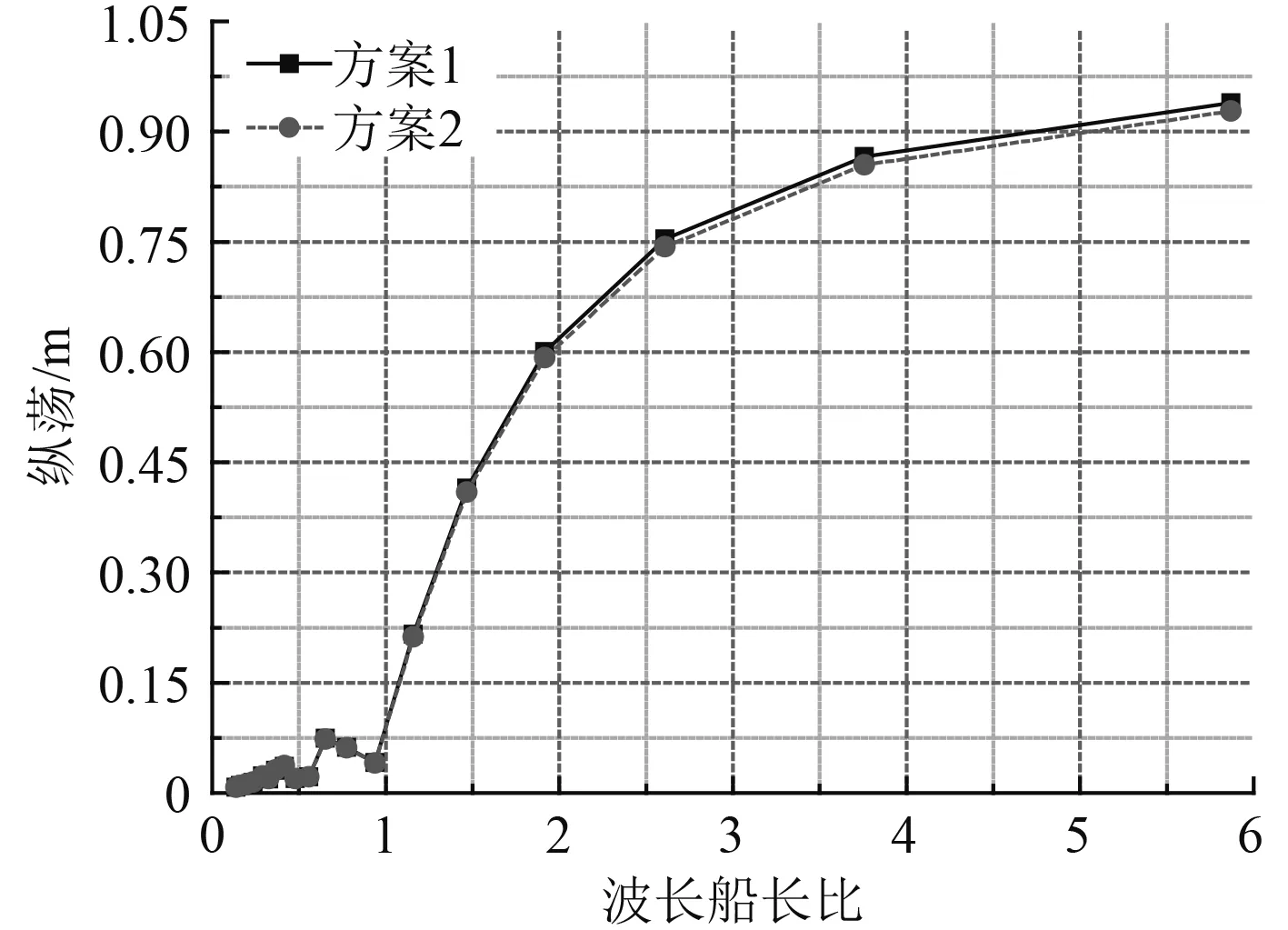
图 5 纵荡幅值对比Fig. 5 Comparison of surge amplitude response

图 6 横荡幅值对比Fig. 6 Comparison of sway amplitude response

图 7 垂荡幅值对比Fig. 7 Comparison of heave amplitude response

图 8 横摇幅值对比Fig. 8 Comparison of roll amplitude response

图 9 纵摇幅值对比Fig. 9 Comparison of pitch amplitude response

图 10 艏摇幅值对比Fig. 10 Comparison of yaw amplitude response

表 2 满载工况下六自由度运动幅值对比Tab. 2 Comparison of motion amplitude of six-degree between caseI and caseII on full load condition

从表2中不考虑浮桥和考虑浮桥影响之后运动幅值的最大值对比可以看出，连接浮桥对船体影响最大的是纵摇，变化率达16.34%，其次是垂荡，变化率是4.74%，而对横荡、纵荡和首摇影响较小，说明浮桥的存在对船体的垂向运动影响较大，而对横向运动和纵向运动影响较小，对横摇的影响几乎为0，这是因为A字型钢架不约束船体的横摇运动。

考虑浮桥影响之后，船体的纵摇和垂荡明显变小，这是因为浮桥的存在使得系统的附加质量和阻尼系数增大，由六自由度耦合运动方程可知，运动幅值将变小。

3.3 载荷响应分析

剖面载荷响应随着剖面位置的变化而变化，因此合理的选取剖面位置非常必要。本文沿船体垂线间长均匀选择了19个剖面，第1个剖面距离船体首垂线的距离为13.125 m，剖面编号沿船尾依次增加。图11～图15给出了考虑浮桥影响之前（图中简称“方案1”）和考虑浮桥影响之后（图中简称“方案2”）的FPSB主船体各剖面的剖面载荷响应对比，包括垂向弯矩，垂向剪力，水平弯矩，水平剪力和扭矩。

表3给出了主船体满载工况下在考虑浮桥影响前后船体剖面载荷幅值的最大值对比结果，以及出现最大值对应的浪向、波长船长比和剖面位置。

图 11 垂向弯矩响应对比Fig. 11 Comparison of the vertical bending moment

图 12 垂向剪力响应对比Fig. 12 Comparison of the vertical shear force

图 13 水平弯矩响应对比Fig. 13 Comparison of the horizontal bending moment

图 14 水平剪力响应对比Fig. 14 Comparison of the horizontal shear force

图 15 扭矩响应对比Fig. 15 Comparison of the torque

表 3 满载工况下剖面载荷幅值的对比Tab. 3 Comparison of section load amplitude between caseI and caseII on full load condition

通过分析图11～图15中船体剖面载荷沿船长的变化规律可知，考虑连接浮桥影响前后，船体剖面载荷达到最大时的剖面位置不发生变化，总体变化趋势不发生改变。

通过分析表3中各剖面载荷幅值在考虑浮桥影响之前和考虑浮桥影响之后的最大值对比，发现考虑连接浮桥影响之后，船体各剖面的垂向弯矩和垂向剪力发生变化较大，垂向剪力的变化率达8.76%，垂向弯矩的变化率为3.16%，而连接浮桥对主船体的水平剪力、水平弯矩和扭矩变化较小，这与连接浮桥对船体的垂向运动影响较大而对横向运动影响较小保持规律一致。

考虑连接浮桥影响之后，船体的垂向弯矩和垂向剪力的幅值总体上呈变大的趋势，这是因为连接浮桥对船体产生的作用力相当于对主船体施加了端部载荷。

4 结 语

针对FPSB与连接浮桥的特殊连接形式，本文分别分析了FPSB主船体与连接浮桥的运动特性，结合三维源汇分布法建立了主船体与连接浮桥的六自由度耦合运动方程，并编制程序进行求解。对连接浮桥影响前后的船体运动与波浪载荷响应进行对比分析，数值结果表明连接浮桥对船体的垂荡和纵摇运动影响较大，计入浮桥影响后船体的垂向弯矩和垂向剪力的幅值总体上呈变大的趋势。本文研究成果对连接浮桥与船体的耦合运动与波浪载荷响应计算具有参考意义。