基于瞬变电磁的采空区含水率评价探讨

王国库，李宏杰，张永超

(1.煤炭科学技术研究院有限公司 安全分院，北京 100013； 2.煤炭资源高效开采与洁净利用国家重点实验室(煤炭科学研究总院)，北京 100013)

含水采空区是煤矿安全生产的重大隐患，我国多起大的煤矿安全事故都是煤矿采掘活动导通采空区积水引起的。采空区及其含水性的探测已经成为各开采企业煤层回采前必须进行的工作[1-2]。地面瞬变电磁法具有易穿透高阻层、对低阻含水采空区反应灵敏、施工方便、效率高等优势，且勘探深度适于煤矿采空区探测，因而迅速成为各大矿区探测采空积水区的首选方法[3]。解海军通过有限元正演和实例指出瞬变电磁法探测采空区积水时虽然有一定的低阻屏蔽效应，但效果良好[4]；梁建刚采用2.5维有限元正演对瞬变电磁法探测采空区的可行性进行了分析，通过对比6个不同深度的充水和不充水采空区模型，得出采空区埋深越大异常出现时间越晚、异常幅度越弱，同时含水采空区引起的异常幅度远大于不充水采空区的结论[5]；邱浩等则对充水采空区进行了瞬变电磁拟地震成像研究，得到了分辨率较高的成像结果[6]；李宏杰等采用井下瞬变电磁法探测上覆采空区的富水性并取得了良好的效果[7]；王伟都采用一维正演和反演的方法研究了瞬变电磁在采空区含水性探测中的应用，并提出运用相对介电常数提高低阻层分辨的方法，但是该研究在正演时并没有明确指出电阻率与采空区含水率之间的对应关系[8]；陈魁奎采用三维积分方程法和物理模拟的方法研究了充水和不充水的单双层采空区的瞬变电磁响应，并采用改进阻尼最小二乘反演方法减小瞬变电磁的低阻屏蔽效应[9]；此外还有很多学者对瞬变电磁法探测采空区富水性进行了大量的研究[10-15]。但是，上述的研究仅关注了采空区是否富水，对采空区的含水率却没有进行进一步的研究。

笔者通过对不同深度不同含水率采空区模型进行一维正演，并采用多项式拟合的手段初步探讨采空区含水率与感应电压增(降)幅间的关系，在某矿的应用实践检验了上述关系的正确性。

1 一维正演算法

本文采用一维正演模拟不同深度及含水率采空区的瞬变电磁响应。整体思路为：先采用快速汉克尔变换计算正演模型的频率域响应，然后采用Gaver-Stehfest法进行逆拉普拉斯变换(简称G-S变换)得到时间域响应，具体算法如下：

水平层状大地上由垂直磁偶极子(水平线圈)激发的垂向磁场[14]频率域表达式为

(1)

(2)

Hz中包含对贝塞尔函数的无穷积分，本文采用快速汉克尔变换对其进行计算，该方法具有采样间隔Δ确定后，滤波系数只需计算一次而无需重新计算的优点。具体如下：

(3)

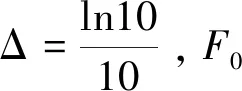
(4)

Vz(ω)=-iωμ0sHz(ω)

(5)

式中，s为接收线圈等效面积。

将式(1)～(4)代入式(5)，即可得到感应电压的频率域响应。

根据瞬变电磁理论，频率域变换为时间域的公式如下：

(6)

根据G-S变换理论，上式经过离散后可写为

(7)

式中，M为取决于精度和稳定性要求的正偶数，本文取16；Km是G-S变换系数，计算方式为：

(8)

2 采空区含水率瞬变电磁评价分析

为了进行采空区含水率的分析，对不同含水率的采空区进行瞬变电磁正演，建立不同深厚比不同含水率采空区的瞬变电磁响应特征正演模型，发射线框边长为200m，接收线圈面积100m2，发射电流1A。模型参数见表1。

表1 地层正演模型

2.1 小深厚比采空区正演分析

覆盖层厚度为80m即采空区的深厚比为4∶1时，一维正演得到的V-t曲线如图1所示。由图1可见，不同含水率采空区的瞬变电磁响应差异明显，除了个别情况(γ=10%)外，它们与实体煤层(即均匀半空间)也有明显差异，表明在理论上采用瞬变电磁探测采空区及其含水率是可行的。具体定性分析，0.1ms之前各曲线基本重合，表明它们浅部的电阻率基本相同；0.1～1ms之间，随着含水率γ的增加，感应电压也随之增大；1ms之后各曲线又趋于重合，反映它们深部的电阻率趋近。此外，由物性特征可知，随着采空区含水率的增加，地电断面会逐渐从K型过渡到H型，图1中的曲线也很好地反映了这种变化趋势。

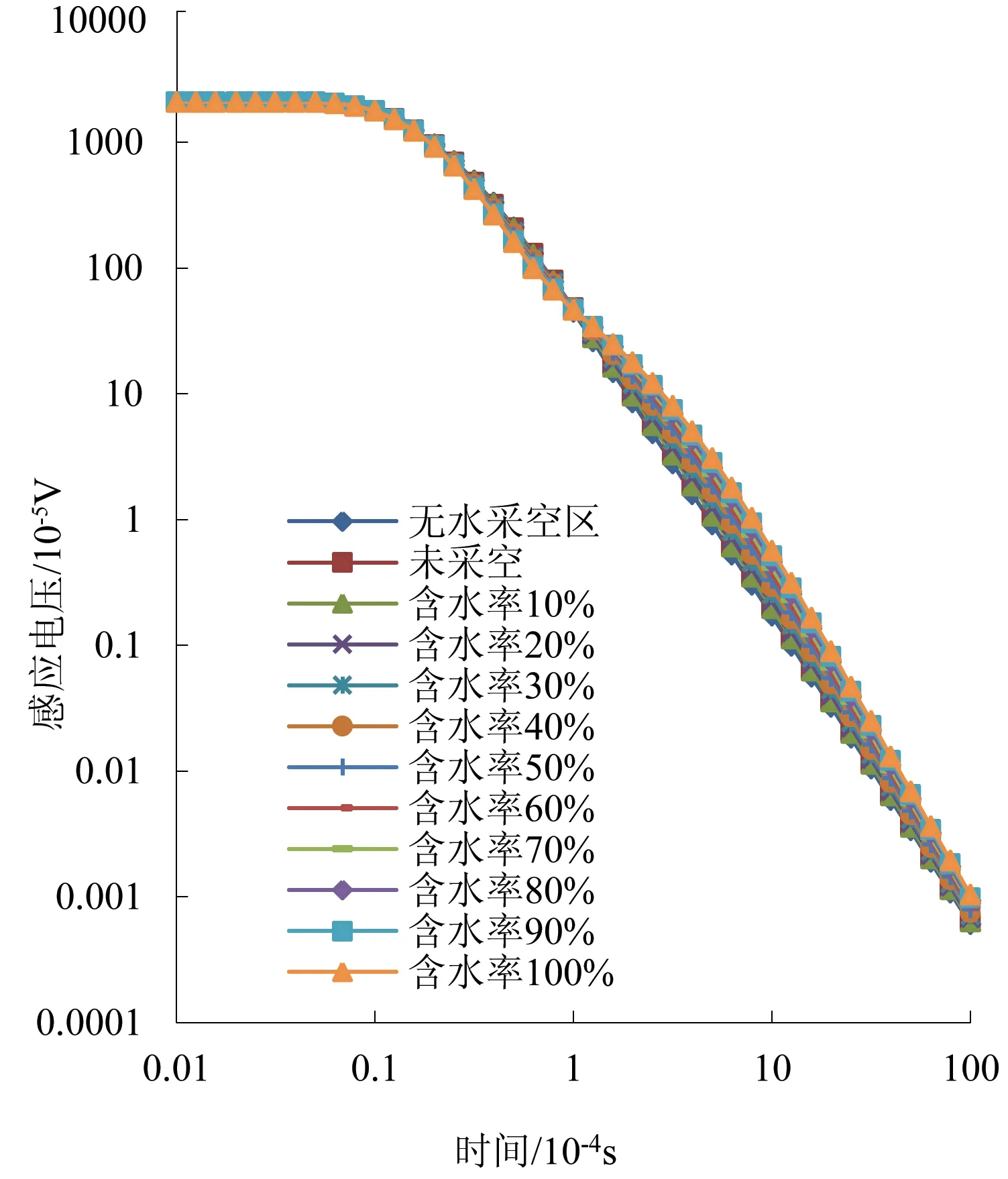
图1 不同含水率采空区模型的V-t曲线(小深厚比)

为进一步进行定量分析，以无采空区时的感应电压为基准，计算了不同含水率采空区对应测道的感应电压增(降)幅(采空区瞬变电磁感应电压与未采空时瞬变电磁感应电压比较)，结果见图2。

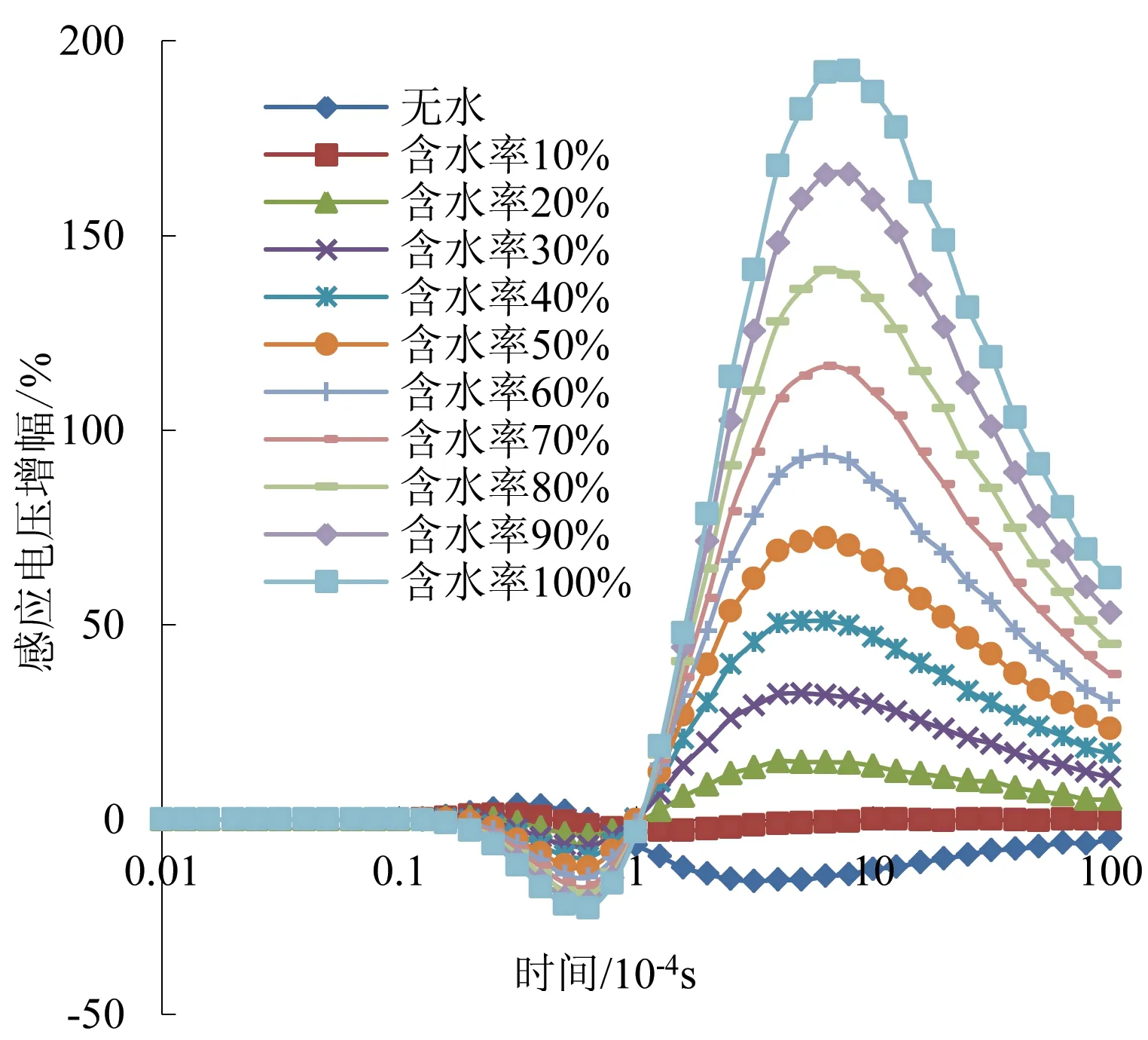
图2 不同含水率采空区的感应电压增幅(小深厚比)

由图2可知，当采空区不含水时，随着地下感应涡流的传播和衰减，首先出现由反射波干涉引起的增幅极大值(称之为Undershoot现象[16])，而后逐渐减小到极小值，但极小值的幅度与极大值相比大很多，这是典型的K型地电断面响应特征。采空区含水率为10%时，在高阻的空气层和低阻的水层共同作用下，其感应电压曲线十分接近无采空区时的曲线，增幅和降幅都不明显。当采空区含水率增减到20%时，首先出现由反射波干涉引起的极小值(称之为Overshoot现象)，而后逐渐增大到极大值，而且极大值的幅度比极小值大的多，呈现典型的H型特征，表明此时低阻的水体开始起主导作用，也说明与高阻体相比瞬变地磁对低阻体更加敏感。此后，随着采空区含水率的增加，曲线特征基本不变，但极值幅度逐渐增大，同时由于瞬变电磁波场传播速度与电阻率成反比，极值出现的时间越来越晚。

由上述分析可见，感应电压增(降)幅的最值基本反映了采空区的富水性且随γ变化明显。据此提取了各模型感应电压增(降)幅的最值(记为Γ1)并经过对比采用2阶多项式拟合了其与γ的关系如下：

Γ1=0.6269γ2+1.469γ-0.1723

(9)

拟合曲线见图3。从前述分析可知，Γ1随γ是单调增加的，因此在相近的地质条件下，根据(9)式即可由感应电压增(降)幅的最值推测采空区的含水率。

图3 感应电压增幅拟合曲线与实际数据对比

2.2 中深厚比采空区正演分析

覆盖层厚度为180m即采空区的深厚比为9∶1时，正演得到的V-t曲线见图4，不同含水率采空区对应测道的感应电压增(降)幅见图5。可见，虽然埋深增大，但是不同含水率采空区的瞬变电磁响应依然有比较明显的差异，只是差异幅度减小(约为h1=80m时的1/2)，出现的时间变晚，曲线随γ的变化规律与h1=80m时基本相同，在此不再赘述。

图4 不同含水率采空区模型的V-t曲线(中深厚比)

图5 不同含水率采空区的感应电压增幅(中深厚比)

按照2.1节中的思路，拟合了感应电压增(降)幅的最值(记为Γ2)与γ的关系如下：

Γ2=0.1956γ2+0.7464γ-0.0782

(10)

2.3 大深厚比采空区正演分析

覆盖层厚度为280m即采空区的深厚比为14∶1时，正演得到的V-t曲线见图6，不同含水率采空区对应测道的感应电压增(降)幅见图7。可见曲线随γ的变化规律与采空区底板埋深h1=180m时基本相同，只是随着埋深的增大，差异幅度进一步减小(约为h1=80m时的1/4～1/3)，出现的时间也进一步变晚。

图6 不同含水率采空区模型的V-t曲线(大深厚比)

图7 不同含水率采空区的感应电压增幅(大深厚比)

感应电压增幅的最值(记为Γ3)与γ间的关系拟合如下：

Γ3=0.0794γ2+0.5177γ-0.05574

(11)

3 采空区含水率瞬变电磁评价应用

以邯郸某矿工业广场下伏采空区的注浆治理效果检测实践，初步检验上述理论的可行性。

检测区域的下伏采空区煤层倾角约20°，采深约200～250m，采厚约5m。注浆选用的材料为含水率超过97%的超高水材料，因此注浆后采空区可视为含水率100%的采空区。

选择采空区底板埋深约250m的测点，根据注浆钻孔的揭露，该处垮落带和裂隙带发育高度约50 m。从式(1)、式(2)可见，典型的K型、H型地电断面的瞬变电磁响应主要取决于h2/h1，ρ2/ρ1的值(对于K型地电断面，当ρ2/ρ1大于某一个值时，其响应主要取决于h2/h1)[14]。因此，注浆前后的瞬变电磁响应特征变化应与2.1节中的模型接近。图8为实测的采空区注浆前后的V-t曲线对比及感应电压增幅。

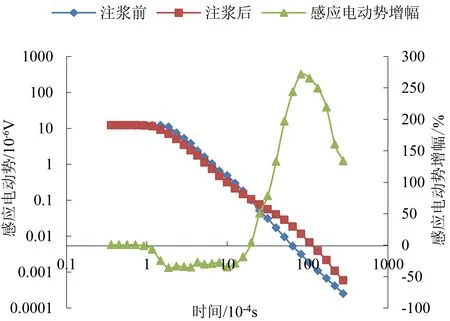
图8 注浆前后V-t曲线对比及感应电压增幅

采空区在注浆前基本不含水，注浆后的感应电压在0.01s前后有明显的增加，根据式(9)，若以注浆前的感应电压为基准，注浆后的增幅约为247%，而实测数据增幅最大值出现在0.0083s，约为271%，相对误差不到10%，考虑到实际地质条件的复杂性以及测量中的干扰等因素，这种偏差是可以接受的。验证了利用感应电压增幅最值分析采空区含水率的可行性。

4 结 论

以正演为手段，对利用瞬变电磁进行采空区含水率评价进行了初步探讨，得出以下结论：

(1)一维正演研究结果表明其他条件相同的情况下，不同含水率采空区的瞬变电磁响应有较大的差异，感应电压随含水率单调增加，采空区的深厚比越大，引起的异常强度越小。

(2)含水率与感应电压增(降)幅最值间的关系可以用二阶多项式拟合，通过瞬变电磁探测采空区含水率在理论上是可行的，实践时可以根据具体的地质条件建立模型进行具体分析。

(3)典型的K型、H型地电断面的瞬变电磁响应主要取决于h2/h1，ρ2/ρ1的值，因此式(9)～(11)也适用于背景电阻率以及深厚比相近的采空区。

(4)实践的初步检验表明了虽然地质条件不尽相同，实际测量也有一定误差，但上述结论仍具有较强的适用性。

由于笔者水平所限，只是在不同深厚比条件下拟合了采空区不同含水率与感应电压的关系，没能同时拟合深厚比和含水率两个因素，在以后的工作中将进一步完善。