基于神经网络和人工势场的协同博弈路径规划

张菁，何友，彭应宁，李刚

1. 清华大学 电子工程系，北京 100084 2. 复杂航空系统仿真重点实验室，北京 100076 3. 海军航空大学 信息融合研究所，烟台 264001

动态环境(包括动态目标和障碍等)下的实时规划是路径规划研究的重要发展方向。其中，多智能体协同和面向博弈环境是当前研究的重点和难点。博弈环境指目标和障碍能够根据智能体当前路径规划决策进行对抗性变化(如改变运动方向等)。面向博弈环境的协同路径规划，即协同博弈路径规划，是空战[1-5]、机器人足球[6-7]等应用场景中的关键问题。

现有研究为解决实时动态路径规划问题对人工势场法展开了大量研究，因为该方法实用性强，具有原理直观、算法结构简单可靠易于实现、对动态环境的适应性好、计算开销小而实时性好、无需预先构建C空间(Configuration space)等优点。现有研究对人工势场法常见的局部最优解[8]、临近障碍目标不可达(Goals Non-Reachable with Obstacles Nearby, GNRON)[9-10]、过狭窄通道时震荡碰壁[11]、动态障碍[12]等问题已能够较好解决。但现有的方法对协同博弈场景考虑不足，环境的对抗性反馈和多智能体协同很难通过规则和策略定量地描述。如何通过人工势场函数系数的动态取值定量反映协同博弈环境是一个难点。基于最优控制的方法虽然可以进行定量的优化，但计算复杂度往往超出实时性的要求。

因此，引入神经网络解决协同博弈问题。近期的基于神经网络的路径规划研究中，一些研究将神经元和神经网络架构映射到构型空间中去，以神经元的输出作为势场引导智能体运动[13-18]；但这一类研究只是利用了神经网络的基本架构和正向传播过程，并未充分利用其学习能力。另一些研究利用神经网络进行路径规划前的知识准备工作，例如预先对环境分类[19]、预测障碍运动模式[20]、计算函数方程[21]等；但这一类研究仅从知识准备的层面提升原方法性能，未能从根本上改进方法能力。相关研究在实际应用中的另一个重点和难点，是高质量、足数量样本的获取，对于战斗机编队空战等场景下的路径规划，很难保证飞行员操作样本的数量和质量。

综上所述，协同博弈路径规划问题面临的难点主要有：协同和博弈的经验、规则、模型的抽象和表达；人工势场函数系数的自适应选取；足够数量的高质量样本的获取。本文提出基于神经网络和人工势场的协同博弈路径规划方法，主要有以下创新点：① 利用神经网络的黑盒特点和学习能力解决协同博弈问题；② 引入神经网络自适应调整人工势场函数系数以解决系数选取难题；③ 将人工势场作为神经网络输出端的特征提取以提升神经网络模块的可解释性；④ 采用遗传算法和滚动时域优化仿真生成高质量样本以解决样本获取难题。

在二对一反隐身超视距空战路径规划中对本文提出的方法进行验证，其获胜率和获胜所需步数均较传统方法有很大提升，且增加的计算开销在可接受范围内。

1 问题模型

以一个具体的二对一反隐身超视距空战路径规划为典型应用来研究协同博弈路径规划问题。

1) 背景。如图1所示，红方战斗机A和B对抗蓝方隐身战斗机。双方飞机均在己方预警机或地面警戒雷达的支持下获得对方粗略位置和航向信息(即瞬时全局信息可知，但全局信息是动态的，下一时刻的全局信息不可预测)，红方战斗机以进入目标区为目的、以避开威胁区为约束，进行协同博弈路径规划。

图1 二对一反隐身超视距空战Fig.1 Two on one beyond-visual-range air combat against stealth

2) 目标区。红方战斗机进入目标区代表其机载火控雷达可以锁定蓝方隐身战斗机，即初步构成导弹发射条件。隐身战斗机对机载火控雷达的雷达散射截面积(Radar Cross-Section, RCS)具有正面小、斜侧面大的方向分布特性[22]，因此目标区在其正面较小而斜侧面较大(即红方战斗机对隐身战斗机斜侧面具有更远的机载火控雷达锁定距离)。将典型隐身战斗机全向雷达散射截面(RCS)模型代入雷达方程，可计算得到目标区边界，如图1所示点线边界，半径最大处在隐身战斗机机头指向的±90°，可达110 km。

3) 威胁区。相当于传统路径规划问题中的障碍区，红方战斗机进入威胁区代表其进入蓝方隐身战斗机的导弹攻击范围。根据空空导弹攻击区计算原理，威胁区主要由蓝方导弹最大射程和双方战斗机相对速度决定，因此红方战斗机A与B因航向不同而具有不同的威胁区，如图1所示虚线边界。根据美国AIM-120空空导弹射程[23]，威胁区最大处出现在双方战斗机迎头飞行时，可达105 km。

4) 基本假设。假设双方战斗机为二维空间内的质点，采用栅格法建立环境空间，栅格粒度按照战斗机实际情况，C空间中的每一格代表现实空域中的1 km，时域上的步长相当于现实中的1 s；双方战斗机始终保持最大速度飞行，其中红方战斗机为非隐身常规战斗机，速度为0.3 km/s(马赫数约为0.9)，蓝方战斗机为新一代隐身战斗机，具备超声速巡航能力，速度为0.5 km/s(马赫数约为1.5)。

5) 初始位置。红方双机采用间距100 km的编队，若以红方战斗机航向作为0°，则蓝方战斗机随机出现在红方双机编队的-90°～+90°方向、距离300 km左右。

6) 判定条件。当红方任一战斗机进入威胁区，为路径规划失败；当红方任一战斗机进入目标区，且均未进入威胁区，为路径规划成功；超过最大步数(设为600步)时红方战斗机仍未进入目标区或威胁区，则为平局。

7) 博弈环境。根据红方战斗机前一步路径规划决策造成的当前位置和航向，蓝方隐身战斗机按照“航向指向最先进入威胁区的红方战斗机”的战术策略实时调整航向。

8) 扩展性。对于其他空战场景中的路径规划问题，也可应用本文方法。例如对于仅具备尾追攻击能力的战斗机，可将对方飞机的尾后区域设置为路径规划的目标区。目标区和威胁区的计算方法可根据具体应用场景调整。

2 方法整体架构

主要由3部分组成：基于人工势场的路径规划模块是基础，基于反向传播(Back Propagation,BP)神经网络的势场函数系数自适应优化模块是解决协同博弈问题的关键，基于遗传算法和滚动时域优化的仿真样本生成模块主要解决空战真实样本难以获取的问题，如图2所示。

首先由基于遗传算法的仿真样本生成模块对典型初始位置情况离线生成近似最优的路径作为样本，牺牲离线计算时间以换取样本的质量。然后使用这些样本离线训练BP神经网络模块。在实时路径规划中采用人工势场法，并在每一时刻以当前相对位置和航向等信息作为输入，通过训练好的神经网络输出势场函数系数。

图2 协同博弈路径规划方法整体架构Fig.2 Architecture of cooperative and adversarial path planning method

3 基于人工势场的路径规划

采用人工势场法，借鉴物理场的思想，在构型空间中构建来自目标区的引力势场和来自威胁区的斥力势场，以产生的合力影响红方战斗机的运动。

1) 引力势场。采用Khatib[24]提出的经典引力势场函数为

(1)

(2)

2) 斥力势场。该斥力势场函数在Khatib方法的基础上引入了本机与目标的距离，在本场景中可以较好避免临障目标不可达问题。采用Ge和Gui提出的斥力势场函数为[9]

(3)

(4)

4 基于BP神经网络的势场函数系数自适应优化

传统的人工势场法在每次路径规划中的势场函数系数是始终不变的，这样就无法对蓝方战斗机的位置和航向变化做出博弈反应，也无法对红方友机的位置和航向变化做出协同反应。因此本文引入一个BP神经网络模块，如图3所示，其中W和b表示神经网络中的参数。以当前时刻本机和蓝方飞机的位置、航向信息及红方友机的位置信息作为输入，输出优化的势场函数系数。为了进一步降低BP神经网络模块输出维度从而提升精度、降低计算复杂度，考虑到合力势场的实质是引力势场和斥力势场的对比，将势场函数系数中的引力增益ka置为1，从而仅需自适应优化斥力增益kr。采用单隐层BP神经网络，8输入单输出，通过试探法和经验数据设置中间隐藏层神经元个数为24，激活函数为Sigmoid函数。

采用BP和带冲量的梯度下降算法，以均方差为损失函数，离线训练神经网络模块以消除训练时间对实时路径规划的影响。训练样本的选取将影响神经网络的泛化性，因此选择6个较为典型的初始位置生成样本，如图4所示，蓝方战斗机分别出现在红方双机编队的前、右前、右方向等。

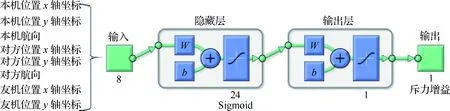
图3 BP神经网络模块结构Fig.3 Architecture of BP neural network model

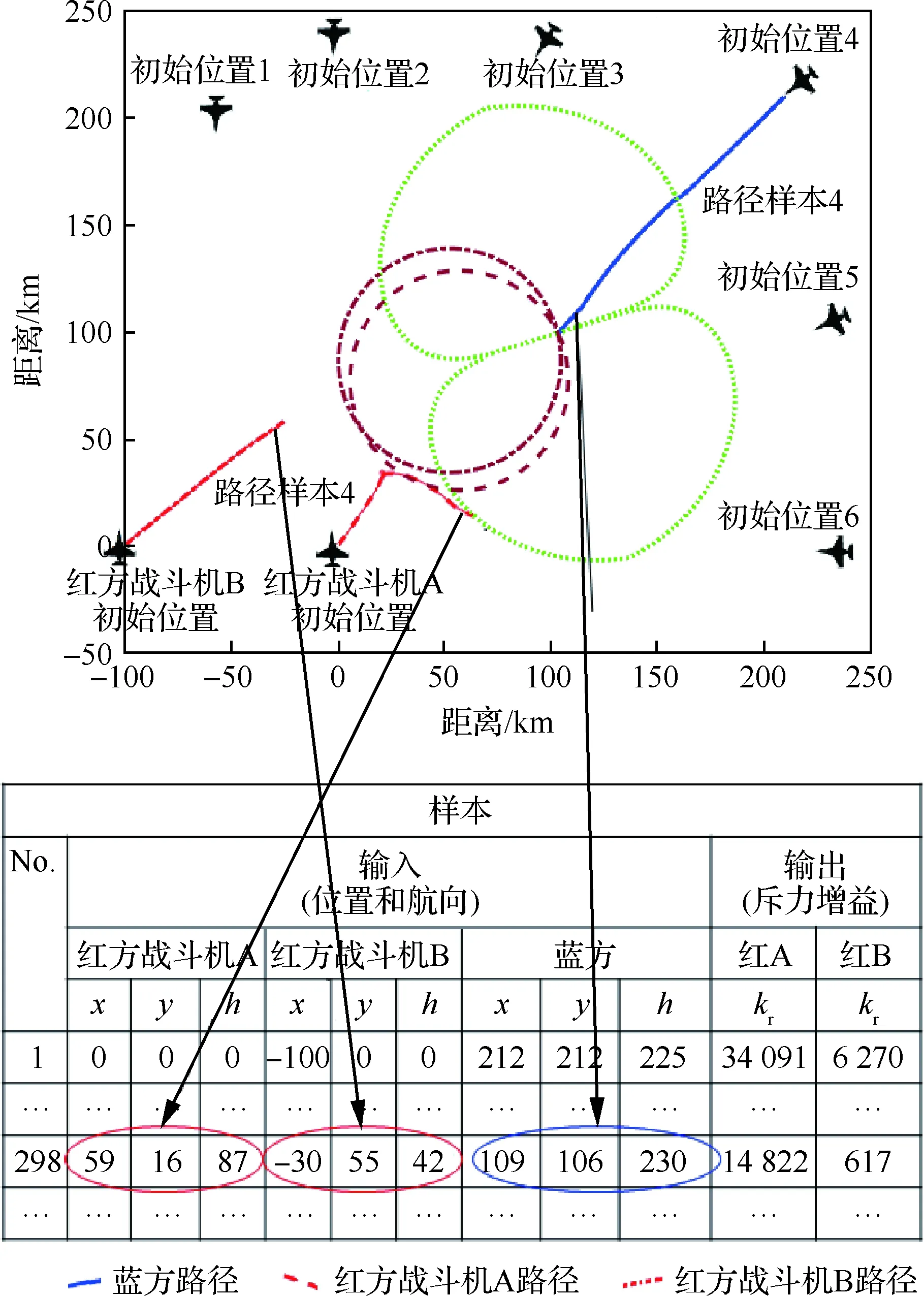
图4 6个典型初始位置及样本转化Fig.4 Initial positions and sample transformations of six typical paths

根据对称性，仅取右方向的样本也可以涵盖左方向的场景。将这些典型初始位置下的近似优化的红方战斗机成功路径按步拆分，每一步作为一个样本。图4下部的表展示了初始位置4时的路径规划如何拆分转化为一组样本，表中每一行为拆分后的一个样本，圈出的示例是第298步转化为第298号样本。

该神经网络模块的正向过程计算复杂度为O(n1n2+n2n3)，其中n1为输入个数、n2为中间层神经元个数、n3为输出个数。当空战场景中的红、蓝方战斗机数量增多时，n1将增大，中间层神经元个数n2和输出个数n3不变，计算复杂度为O(n1)，扩展性较好。

5 基于遗传算法滚动时域优化的仿真样本生成

基于BP神经网络的自适应优化效果很大程度上取决于训练神经网络时使用的样本质量和数量。对于军事航空应用：从样本质量方面，难以确保飞行员真实操作产生的路径每一步都是最优解；从样本数量方面，获取足够数量的飞行员真实操作样本需要付出较高的成本。

本文采用仿真生成样本的方式，分别对红方两架战斗机及前面选定的6个典型初始位置，使用人工势场法进行路径规划。规划中每前进一步，均通过遗传算法寻找基于当前相对位置和航向的、使后面路径规划成功且所需步数最小的势场函数系数，然后更新该势场函数系数并前进一步，再停下调用遗传算法优化更新下一步的势场函数系数。这也可以看作一种特殊的滚动时域优化，时域窗口是从当前时刻到路径规划结束。具体算法流程如图5所示，下面进行详细解释。

1) 编码。将引力增益、斥力增益等势场函数系数各视为一个基因，共同组成一条染色体

Xi=[ka,kr, …]i∈[1,M]

(5)

图5 基于遗传算法滚动时域优化的仿真样本生成Fig.5 Genetic algorithm receding horizon optimization based samples generation

式中：M为种群规模，种群中的每个个体仅含一条染色体。由于本文采用比例缩放的思想将引力增益ka置为1而仅需优化斥力增益kr，染色体将仅包含斥力增益。

2) 生成初始种群。初始种群中将包含路径前一步使用的势场函数系数，这也是精英策略在路径规划层面的应用，在后面的遗传操作中也将应用精英策略在遗传迭代中保留最优个体，属于遗传算法层面的应用。

3) 适应度。适应度用于描述染色体优劣，在遗传迭代中适应度高的染色体留下继续发展，适应度低的染色体被淘汰。本文设计的适应度函数如式(6)所示，其中F为适应度，S为成功所需步数。式(6)的物理意义是：使路径规划成功的势场函数系数适应度高于使之平局和失败的，在使之成功的势场函数系数中达到成功所需步数越小的适应度越高。

(6)

4) 遗传操作。使用轮盘法筛选种群，对选出的个体进行交叉和变异，采用精英策略，在重插入时选择交叉变异后适应度较高的个体替代原种群中适应度较低的个体，同时保留原种群中的精英。

5) 录入样本。最终生成的路径上的每一步可生成两个样本，分别是红方战斗机A和B。每一步的本机和蓝方战斗机的位置、航向信息及红方友机的位置信息作为样本的输入部分，每一步的遗传算法优化结果作为样本的输出部分。

6 验 证

对本文提出的基于神经网络和人工势场的协同博弈路径规划方法及基于遗传算法的仿真样本生成算法进行验证：一方面与Khatib提出、Ge和Cui改进的经典人工势场法路径规划进行对比，经典人工势场法虽提出较早但通用性强、认可度高，是众多改进方法的基础和参照对象；另一方面与直接使用神经网络进行对比，验证以人工势场作为神经网络输出端特征提取的价值。

在Intel i7处理器和8 GB内存的64位Windows 7系统上通过MATLAB进行仿真。按照常见的空战场景和武器装备性能设定仿真环境参数。

6.1 路径规划直观效果

通过一个典型样例直观地验证采用本文方法的路径规划效果。选取蓝方战斗机出现于红方战斗机A航向右前方的情况，即蓝方战斗机初始位置坐标(212, 212)、初始航向225°，结果如图6所示。采用经典方法时，如图6(a)所示，由于势场函数系数不能自适应优化：一是造成红方战斗机的路径规划对蓝方战斗机调整航向接近或离开并不敏感，缺乏博弈；二是造成红方两架飞机虽然相距蓝方一近一远，路径趋势却相似，未能产生协同。最终的路径规划结果是失败。同样场景下采用本文方法时，路径规划结果如图6(b)所示，斥力增益根据实时相对态势自适应优化如图6(d)所示，将斥力增益变化与路径对应分析：如图中箭头1所示，红方战斗机B由于距离蓝方战斗机更远，斥力增益自适应减小以使其快速接近蓝方战斗机，对友机形成支援，这是协同能力的体现；如图中箭头2所示，路径规划末段红方战斗机即将进入目标区或威胁区，当蓝方战斗机航向指向本机时斥力增益显著增大以逃离威胁区，当蓝方战斗机航向偏离本机后斥力增益迅速回落以趁机逼近目标区，这是博弈能力的体现。最终的路径规划结果是经353步成功。基于遗传算法获得的近似最优路径是经317步成功，如图6(c)所示，可见神经网络较好达到了样本的效果。

图6 路径规划结果Fig.6 Results of path planning

6.2 路径规划总体性能与开销

验证本文方法在大样本量下的性能和计算开销，并与经典方法对比,如表1所示。样本组包括1 000个随机初始位置的路径规划，统计结果显示，对比经典方法，本文方法的成功率显著提升达32.3%，成功所需步数减少了约15.37%，充分表明了本文方法对路径规划性能的提升。另一方面，虽然神经网络正向传播过程引入了额外的计算开销，使其增加了4个数量级，但依然在毫秒量级，考虑到未来实际应用中还将获得进一步软硬件优化，本文方法的计算开销是可以接受的。

表1 总体性能与开销Table 1 Overall performance and cost

6.3 神经网络训练性能

验证对单隐层BP神经网络模块的训练性能。将样本归一化，随机分为训练集、验证集和测试集，采用冲量梯度下降算法进行训练，100 000轮训练后均方误差下降达3个数量级，如图7所示。

图7 神经网络训练性能Fig.7 Performance of neural network training

6.4 遗传算法滚动时域优化性能

验证生成仿真样本的遗传算法的性能。设置遗传算法的参数为：初始种群规模为20，遗传迭代50轮，交叉率为1，变异率为1，重插入比例为0.8。图8所示为在蓝方战斗机初始位置坐标(-50, 300)、初始航向180°时的路径规划中，对红方战斗机A第1、207步和对红方战斗机B第186步的遗传算法优化效果。可见，随着遗传迭代轮数(由x轴表示)的增多，种群中最优个体和种群平均的距离路径规划成功所需步数(由y轴表示)不断减小。图8(b)所示红方战斗机B在第186步通过遗传算法优化使得路径规划成功所需步数减少了30。当路径规划的结果是平局或失败时，该步数为无穷大，因此图8(b)所示红方战斗机A第1步在遗传迭代前十余轮均无解，种群平均值曲线的断点是因为种群中有平局或失败的样本。

对6个典型初始位置的路径规划进行遗传算法优化，定义优化率为减少的步数与原步数之比，如式(7)所示，其中S′为采用新方法后的步数，R为优化率。当路径规划结果为失败时，可视为需要无穷多步才能达到成功，即S=+∞，代入式(7)计算，此时R≈100%。

图8 遗传算法对典型步样本的优化性能Fig.8 Performance of genetic algorithm based sample generation on typical steps

(7)

可见遗传算法对于生成优化的仿真样本具有普遍有效性(如表2所示)。

表2遗传算法对典型路径规划的优化性能

Table2Performanceofgeneticalgorithmbasedsamplegenerationontypicalroutes

蓝机初始位置蓝机初始航向/(°)经典算法步数GA优化后步数优化率/%(-50,300)180Loss287≈100(0,300)18033429112.87(150,260)210Loss339≈100(212,212)225Loss331≈100(260,150)24044234921.04(300,0)270Loss420≈100

6.5 协同博弈性分析

神经网络模块内部是一个黑盒，具有不可解释性，本节从其输入数据和输出数据的对应变化，① 分析红方友机之间的相对位置、速度关系对红方战斗机下一步运动的影响，即协同特性的体现；② 分析对方战斗机对本机的运动趋势对本机下一步运动的影响，即博弈特性的体现。

首先定义两个概念，如图9所示：距离差(Distancedelta)为本机到蓝方战斗机距离减去友机到蓝方战斗机距离，反映了红方战斗机的协同阵位是否均衡；航向差(Headingdelta)为蓝方战斗机航向与蓝方战斗机到本机连线的夹角，反映了蓝方战斗机航向是指向还是偏离本机，是博弈的基础。

图10(a)为样本中距离差与输出的斥力增益的关系，距离差为负时意味着本机相比友机距蓝方战斗机更近，图中可见此时斥力增益增加以减缓接近蓝方战斗机，等待友机跟上支援，从而体现出协同特性。

图9 距离差与航向差Fig.9 Difference of distance and difference of heading

图10 样本中距离差和航向差与输出斥力增益的关系Fig.10 Data relation between difference of distance and difference of heading and repulsive gain coefficient

图10(b)为样本中航向差与输出的斥力增益的关系，航向差为0°时意味着蓝方战斗机正以本机为目标接近，图中可见此时斥力增益增大以逃离威胁区；航向差绝对值增大时意味着蓝方战斗机正偏离本机，图中可见此时斥力增益降低以趁机接近蓝方战斗机目标区，这体现出博弈特性。

6.6 人工势场作为神经网络输出端的特征提取

将本文提出的人工势场与神经网络结合的方法与直接使用神经网络的方法进行对比。直接使用神经网络时，输入项设置与本文方法相同，不同的是直接以航向作为输出。样本均基于遗传算法仿真生成。仍以蓝方战斗机初始位置坐标(-50, 300)、初始航向180°时的路径规划为例，图11所示为直接使用神经网络的路径规划结果，可见红方战斗机并未体现出逼近目标区和规避威胁区的运动趋势，更未体现出协同和博弈能力，而是红方战斗机B在中途进入原地盘旋，红方战斗机A直接冲入威胁区，导致路径规划失败。这是由于跳过人工势场法，直接使用神经网络时，输入与输出数据的相关性过于复杂，不具备6.5节中描述的距离差与斥力增益、航向差与斥力增益的相关性。由此可见本文方法将神经网络与人工势场结合的意义，通过人工势场在神经网络输出端进行特征提取，其中势场函数系数即为特征。

图11 使用神经网络的路径规划结果(不带人工势场)Fig.11 Path planning results by neural network (without artificial potential field)

7 结 论

1) 基于神经网络和人工势场的方法对于协同博弈路径规划问题具有较好的性能和可接受的时间开销，可应用于编队空战、多机器人对抗性比赛等场景下的路径规划。

2) 基于遗传算法和滚动时域优化来生成仿真样本，能够替代人工真实样本，解决神经网络训练样本质量和数量不足的问题，可应用于空战、对抗性比赛等样本获取难度大的场景。

3) 人工势场可视为在神经网络输出端进行的特征提取，比直接使用神经网络有更好的性能和时间延迟，同时提升了神经网络的可解释性。