状态预测神经网络控制应用于小型可回收火箭
陈书钊,楚龙飞,杨秀梅,蔡德淮
1. 翎客航天科技有限公司,北京 100176 2. 昆明理工大学 信息工程与自动化学院,昆明 650500
可重复使用运载器(Reusable Launch Vehicle, RLV)是指能够在地球表面与太空之间重复往返的多用途飞行器[1-2],分为部分可重复运载器和完全可重复运载器。具备可重复使用、可靠性高、维护成本低等特点的运载器,根据费用均摊的原则,可有效降低单位载荷的发射成本[3]。
麦道与NASA合作于20世纪90年代研发一种火箭动力单级入轨飞行器DC-X,其通过控制发动机推力实现了飞行器的垂直起飞和垂直降落(VTVL)技术,是RLV的早期雏形。后来由于一些原因,DC-X项目最终被放弃。但是DC-X项目为RLV的发展开辟了新的道路。DC-X项目的一些工程师后来进入了蓝色起源(Blue Origin)专注于RLV的研发,并于2005年通过Charon原理样机完成了VTVL技术验证,其随后又进行了大量相关试验,并通过New Shepard-1,于2015年成为第1个具有VTVL技术且进入太空的民营航天公司。同时DC-X项目也为Armadillo航空航天、Masten空间注入了灵感,这两家民营航天公司分别通过自己研发设计的Mod和Xombie两个具备VTVL功能的飞行器获得了2008年和2009年的XPRIZE最高奖,为RLV的发展注入了活力。
SpaceX太空探索公司是最晚研发RLV的公司,却是迄今为止走的最远的公司。其用Grasshopper火箭于2012年开始研发VTVL技术,2015年其Falcon-9火箭将卫星送入轨道之后成功完成陆地回收,实现人类航天史上一个重大里程碑。2018年2月SpaceX“重型猎鹰”(Falcon Heavy)取得重大成果,其助推器和芯级都具备可回收能力,成为具备可部分重复使用能力的现役最大运载火箭。
运载火箭的重复利用通常包括4项关键技术[4]:精确高效的控制技术、可以变推力和重复使用的发动机技术、高可靠的着陆支撑技术、快速检修再利用技术。而垂直起飞与垂直降落技术则是前3项技术的结合。精确高效的控制技术包含了制导系统、动力控制系统、姿态控制系统和其他控制系统。火箭在回收的过程中制导系统对精确着陆起着至关重要的作用,对此SpaceX和Masten两家公司分别在文献[5-6]中进行了详细讨论,同时关于可回收火箭的制导技术也存在大量研究[7-8]。但关于可回收火箭的动力控制系统研究却很少,SpaceX和Masten也并未透露更多信息。翎客航天作为世界上继SpaceX之后第六家掌握了VTVL技术的商业航天公司,本文将详细讨论其在VTVL技术动力控制系统方面所做的创新。
动力控制系统是根据火箭的飞行状态直接参与发动机推力控制的系统,控制效果的优劣决定着火箭回收的成败。由于目前VTVL技术在世界上还属于非常前沿的技术,其相关参考文献极其有限,而关于VTVL技术中非常关键的动力控制系统方面的参考文献目前还没有。动力控制系统可以通过经典控制理论的方法进行设计,即在已知被控对象较为精确的模型的情况下设计控制器结构,通过稳定性计算确定参数进而获得使系统稳定的控制器。然而这种思路对于一个民营商业航天公司意味着很大的成本付出,因为被控模型的精确程度取决于加工工艺,而目前所有满足航天标准的加工工艺都意味着巨大的成本。因此对精确程度较差的被控模型实现稳定控制,成为民营商业航天公司一个较大的需求。
翎客航天基于3 000 N深度可变推力(10%~110%)发动机LinkPower-3,于2015年开始研发RLV技术,并依靠民间工业力量制造了一系列代号为RLV-T小型可回收火箭验证机,并于2018年初通过RLV-T3成功掌握了VTVL技术。相较于科研院所代表国家力量研制出的大型火箭,该系列火箭存在一些特殊的技术难点,比如其质心位置测算和惯量测算有较大误差,机械传动有较大误差等。这一系列技术难点导致被控对象的模型不准确,计算可以保证稳定的控制器却难以实现稳定控制。为了实现对RLV-T3的稳定控制,翎客航天独立研发了一种称为状态预测神经网络控制(State Prediction Neural Network Control, SPNNC)的智能控制算法[9-10]。该算法可以在已知被控对象粗糙状态方程(线性)的情况下,通过调整一个主要参数和一个辅助参数实现稳定控制,可应用于所有可以经过线性状态方程实现预测的单输入单输出(SISO)系统和多输入多输出(MIMO)系统。基于神经网络的控制器种类有很多,而SPNNC的创新点在于将状态方程用于预测并与神经网络的优化性能相结合从而实现强鲁棒性的控制。SPNNC不需要离线训练、计算简单且迅速、容错能力强、通用性强。同时,将这种新的控制算法大胆地应用于火箭回收技术,也是航天领域的一次创新,是商业航天灵活性的体现。
1 算法设计
1.1 神经网络控制算法
人工神经网络(简称神经网络)是人类根据动物中枢神经系统(尤其是脑)的结构和信号处理机制构建的一种处理实际问题的数学模型[11]。而将人工神经网络应用于控制系统可实现智能控制,具有可控复杂(如非线性、快时变、多变量、环境扰动等)系统,高容错性能,多模态组合(定性决策和定量控制相结合)控制等特点[10]。基于神经网络的控制器具有非常多的种类,如基于自适应方式的神经网络控制器,由神经网络单独组成的控制器,神经网络与比例-积分-微分(PID)、预测控制、内模控制等传统控制结构结合形成的神经网络控制器,神经网络的智能控制,神经网络优化控制等[11]。而本文要介绍的SPNNC正是结合神经网络的优化性能与状态空间预测性能于一体的在线学习控制算法。
该算法包括2个核心部分,即神经网络部分和状态预测部分。其中神经网络部分的作用就是尽可能地使被控对象的输出和参考量一致,而状态预测部分的作用就是为了规避系统时滞导致的控制失步,将神经网络产生控制的时间点和被控系统产生作用的时间点尽可能地保持在最小区间内。神经网络部分可认为只起到一个优化器的作用,当被控对象为简单SISO系统时,可以将神经网络简化为单神经元进行控制,其优点是计算简单迅速、逻辑清晰。当被控对象为特定情况的MIMO系统时,即可通过状态方程对未来进行预测,则神经网络部分采用多层网络(如BP(BackPropagation)神经网络)进行控制,其优点是可以实现复杂系统较好的控制。RLV-T3小型可回收火箭验证机的高度控制正是使用了单神经元进行的,第3节将会对该控制进行详细说明。
本算法采用BP神经网络[11]作为控制器,通过在线学习的方法能够很好地保证系统的稳定性。同时对于该算法,修改网络的输入输出可以实现对多输入多输出系统的控制。
Simulink中,SPNNC对SISO系统的控制结构如图1所示。虽然BP神经网络有很多优点,但对于本文设计的算法并非必需,因为对于简单的SISO系统,BP神经网络可以直接用单神经元进行代替。用单个神经元代替BP神经网络作为控制器进行控制,对于简单SISO系统不仅不会影响控制器的控制效果,而且结构简单、计算耗时短、收敛快[11-13]。关于用单个神经元进行控制将会在下面的小节中详细介绍。

图1 状态预测神经网络控制结构Fig.1 Structure of State Prediction Neural Network Control (SPNNC)
1.2 在线学习神经网络控制器结构
图1中神经网络控制(NNC)部分在进行控制之前需对数据做预处理,即保存当前误差e(k),并将e(k)、e(k-1)、e(k-2)作为神经网络的3个输入同时送入BP神经网络控制器模块。BP神经网络控制器会对优化目标进行优化,计算出控制量u(k),然后将控制量u(k)输入到被控对象中参与控制。
BP神经网络控制器的网络结构如图2所示。其中隐层神经元的个数可因不同情况进行调整。

图2 3输入1输出BP神经网络结构Fig.2 BP neural network structure of 3 inputs and 1 output
当将SPNNC应用于特定情况(系统未来的状态可以通过状态方程进行预测)的MIMO系统时,BP神经网络将采用如图3所示的结构。其中每一个参考量rs与反馈ys的差相邻的3个时刻值对应神经网络输入层的3个神经元xs1、xs2、xs3,输出层的ys对应被控对象的控制输入。
对于SISO系统,图2中的神经网络可以用单神经元结构代替,如图4所示。
对于图3更为一般的结构,其前向计算过程用矩阵可表示为

图3 MIMO系统中BP神经网络控制器结构Fig.3 BP neural network control structure in MIMO system

图4 单神经元结构Fig.4 Single neuron structure

(1)
优化指标为
(2)
式中:X为输入向量;Hi和Yi分别为参与激活函数运算前隐层和输出层的数据向量;Ho和Yo为激活函数运算后隐层和输出层的数据向量;f1(·)和f2( ·)分别为隐层和输出层的激活函数;Whx和Wyh分别为输入层到隐层和隐层到输出层包含了偏置量的权重矩阵;rs和ys分别为MIMO系统中第s个参考量和第s个系统输出量;S为输入输出总数。
当使用梯度下降法对式(2)的指标进行优化时,仅需对当前的ri、yi(i=1,2,…,s)进行优化,而无需对历史数据进行优化。另外,还有一项被控对象关于输入控制量的偏导数未知,故假设被控对象与输入控制量的关系满足:
y=G(u)
(3)
(4)

根据以上提供的关系,即可实现神经网络的在线学习与前向计算,进而对被控对象进行控制。
1.3 状态方程实现的预测
状态空间模型本质上是将动力系统的高阶微分方程降为一阶多变量微分方程组。对于一个线性系统,可用状态空间模型表示为[14]

(5)
式中:x′(t)∈Rn为状态向量;y′(t)∈Rq为输出向量;u′(t)∈Rp为输入向量;A′∈Rn×n为状态转移矩阵;B′∈Rn×p为输入矩阵;C′∈Rq×n为输出矩阵;D′∈Rq×p为前馈矩阵(通常为0);t为系统时间。为了形式上易于理解,以上变量右上角的“′”仅表示不同的变量,而不是数学运算。在给定初始值的情况下,计算式(5)所示微分方程的解,可得

(6)
式中:
(7)
取t=kT(k=0,1,2,…),T为离散系统采样周期。即可将式(5)离散化:

(8)
式中:x(k)=x′(kT)∈Rn为状态向量;y(k)=y′(kT)∈Rq为输出向量;u(k)=u′(kT)∈Rp为输入向量;A=(I+A′T)∈Rn×n为状态转移矩阵;B=B′T∈Rn×p为输入矩阵;C=C′∈Rq×n为输出矩阵;D=D′∈Rq×p为前馈矩阵(通常为0)。
同时式(7)可变为
Φ(k)=Φ′(kT)=eA′kT=I+A′kT+
(9)
将式(9)泰勒展开取前两项,做如下近似:
Φ(k)=Φ′(kT)=eA′kT=(eA′T)k≈
(I+A′T)k=Ak
(10)
因此式(6)可变为
(11)
式(11)也可以写为
(12)
式(11)和式(12)的区别在于加和的顺序,形式不同而结果相同。
式(11)和式(12)同样可以通过式(8)中状态转移方程的累加求和得到,2种计算方式的结果相同。下面的计算中统一使用式(12)。
式(11)和式(12)都是在u(0)~u(k)已知的情况下基于0时刻状态量计算k时刻的状态量,为了将式(12)应用于系统未来行为预测,需对其做适当调整。当系统处于k时刻,并对系统的k+M时刻进行预测时,系统控制输入u(k)~u(k+M)是未知的,为了实现较为合理的预测可作如下假设:
u(k+i)=ρ(i)u(k)
(13)
式中:ρ(i)为系数。
系统处于k时刻时,对k时刻到k+M时刻的系统输入u(i)可以作各种更为合理的假设,而且系统控制输入u(i),(i=0,1,…,M)也并非一直起作用。可以假定控制输入只在前P(P≤M)个周期起作用,而之后的M-P个周期无控制输入。综上所述,式(12)可表示为
(14)
由式(8)可知,当D=0时,式(8)第2式变为
y(k+M)=Cx(k+M)=CAMx(k)+
(15)
当M、P、ρ(i)确定后,式(15)可以进一步简化为
y(k+M)=αx(k)+βu(k)
(16)

因此系统式(8)即变为

(17)
式(17)即为状态转移方程、输出方程和预测方程。将式(17)与神经网络控制算法结合,即可实现单点预测控制。
1.4 状态预测神经网络控制应用于MIMO系统
多变量系统又称多输入多输出系统,是指系统内部存在多个变量,且普遍存在耦合的复杂系统,如图5所示。
对于MIMO系统可以采用各种各样的解耦控制[15-19],本文提出的SPNNC也可以对含有特定特征的MIMO系统进行解耦控制。这种特征即:系统时滞小或者可以通过一定方法(状态空间法等)对系统未来进行预测(或粗估计)。式(17)描述的预测方法仅限于线性系统,而非线性系统则需要线性化。对于时滞小的系统可以省去对未来的预测部分,直接使用神经网络进行控制。而对于时滞较大的系统,则必须对系统的未来进行预测,进而实现稳定控制。
对于RLV-T3小型可回收火箭,所有控制通道均可简化为SISO系统,即无需进行解耦控制。为了验证SPNNC对MIMO系统的控制效果,2.2节将通过Simulink仿真方法对此进行说明。

图5 MIMO系统Fig.5 MIMO system
2 RLV-T3小型可回收火箭与Simulink仿真
2.1 RLV-T3小型可回收火箭概况
RLV-T3小型可回收火箭高为4 500 mm,储罐直径为450 mm,起飞质量为300 kg,燃料体系为LOX-EtOH,配备一台3 000 N可深度变推力(10%~110%)矢量发动机。RLV-T3的整体外观如图6所示。关于电气部分,该火箭带有一个姿态传感器、一个3轴加速度传感器、载波相位差分(RTK)系统、发动机摆角传感器、各储罐压力传感器、燃烧室压力传感器、点火系统、阀门控制系统、灭火系统、无线传输系统、电动系统、电源管理系统和安控系统。因为该型号火箭的研制只是为了验证火箭整体性能和低空火箭回收技术,无需应对高速、高温、高压等极端工况,故整箭的姿态控制和推力控制仅通过一个二自由度可摆动矢量发动机实现。在箭体飞行过程中,沿箭体方向的旋转是一个干扰小项,由于仅有一台矢量发动机,无能力也无必要对该方向的旋转进行控制,在实际飞行过程中也验证了该论断。
由于民间工业制造能力的限制,该型号火箭在制造过程中相较于航天院所内各机械结构精度指标略低、电气技术可靠性略差,对箭体的稳定性控制造成一定压力。对箭体的控制主要存在以下难点:RTK数据采样频率略低(10 Hz)、RTK天线容易受遮挡物的影响(箭体转动会产生影响)、箭体产生的剧烈振动对加速度传感器影响较大、发动机推力关于流量阀圈数之间呈非线性关系、系统时滞、步进电机对流量阀的机械传动存在间隙、在飞行过程中箭体是一个变质量变质心物体、发动机推力线可能与重力线不相交引起箭体自身旋转、低温液氧容易受环境影响造成压力不稳定进而影响发动机推力不稳定以及箭体结构易发生变化进而质心惯量发生变化等。

图6 RLV-T3小型可回收火箭整体外观Fig.6 Overall appearance of RLV-T3 small reusable rocket
2.2 RLV-T3高度SISO系统的控制仿真
为了研究上述算法的可行性,现通过Simulink仿真进行分析。根据RLV-T3小型回收火箭自身动力系统、控制系统的基本参数建立仿真模型,对高度控制进行仿真分析。被控对象模型的精细程度会影响控制算法参数,进而影响控制效果。
RLV-T3采用了氮气增压,在整个飞行过程中氮气压强大于4 MPa。燃料储罐和液氧储罐通过减压阀与氮气相连,并在飞行过程中保持在3.5 MPa。推进剂通过管路经过流量阀后汇入发动机,控制系统根据传感器采集的数据计算后控制流量阀和发动机摆角执行机构。流量阀会根据控制指令打开适宜的开口通径控制推进剂流量,进而使发动机产生适宜大小的推力,以保证箭体达到预定的运动效果。而发动机摆角执行机构则根据箭体运动状态控制发动机推力的方向,进而控制箭体的运动。
高度传感器采用的是0.03 m精度、10 Hz采样频率的RTK,该传感器可以提供经纬度和高度三维信息,利用这些信息实现闭环控制。流量阀通过步进电机进行控制,而步进电机通过处理器输出一定数量的脉冲到电机驱动进行控制,每一个脉冲可对应步进电机转过对应的角度,因此
dθ=k1u(t)dt
(18)
式中:k1为比例系数,而步进电机转过的圈数可表示为

(19)
式中:τ0为控制量从产生到完成存在的延时。在推进剂储罐压强固定的情况下,假设发动机产生的推力与流量阀圈数之间的关系满足:
F(t)=f(C)=f{C[u(t)]}
(20)
假设火箭在飞行过程中推进剂秒耗量满足:
(21)
则飞行过程中火箭整体实时质量为
(22)
由牛顿第二定律可知
F(t)-m(t)g=m(t)a(t)
(23)
式中:g为没有方向的重力加速度常数。即得
(24)
加速度经过两次积分可得
(25)
将上述过程整理后得
h(t)=F(u(t))
(26)
即箭体高度与控制量脉冲数的关系是非线性关系,且其中推力与流量阀圈数的关系式(20)也是非线性关系,因此无法准确地得到其传递函数。其结构如图7所示。
该被控对象具有复杂的非线性环节,使用经典控制理论的分析方法难以获得系统稳定的参数。而对于RLV-T3的真实情况,其物理结构易发生变化,系统特性变化范围大,对控制器的鲁棒性要求很高。对于此复杂的非线性系统,使用SPNNC可以仅取其重要的线性环节,而忽略掉非线性环节。即仅考虑其加速度积分到位移的部分,并据此列出系统方程对系统未来进行预测,因为通过下面的试验可以看出,SPNNC极强的鲁棒性可以容纳这些控制误差。
下面建立离散时间状态预测神经网络控制器:
如前所述,对于SISO系统可以将神经网络简化为一个神经元实现控制。对于图4的单神经元,设参考量与预测反馈值的差为
e(k)=r(k)-y(k+M)
(27)
设神经元输入向量为
X(k)=Li×[e(k)e(k-1)e(k-2)]T
(28)
式中:Li为入口系数。设权重为
(29)
设激活函数为
(30)
则神经元的前向计算为
(31)
式中:Lo为出口系数;b为偏置量。入口系数和出口系数是为使神经元的优化性能最大化而定的常数,因不同被控对象而异。
优化指标为
(32)
对于状态预测部分,仅需考虑箭体遵从牛顿第2定律而产生运动的部分,即设状态量为
x=[vh]T
(33)
则式(17)变为

(34)

(35)
其中:T为控制周期;ρ(i)为权重序列;P为加速度项作用长度;M为预测步长。
当面对不同的被控对象时,控制周期T是固定的,权重序列一般由1到0均匀取P个数。对于具有线性运动特征的被控对象,式(34)都不变,所以对于不同的被控对象,主要调整P和M,以及辅助调整Li、Lo即可。对于图7的被控对象,经过调整以上参数后,控制器对阶跃信号的响应如图8所示。控制器对正弦信号的响应如图9所示。从图8和图9可知该算法响应时间4 s,对周期大于8 s的正弦信号幅频特性跟随良好。

图7 RLV-T3高度控制通道被控对象Fig.7 Controlled plant of height control channel of RLV-T3

图8 SPNNC对阶跃信号的响应Fig.8 SPNNC’s response to step signal

图9 SPNNC对正弦信号的响应Fig.9 SPNNC’s response to sinusoidal signal
2.3 SPNNC与PID控制器的比较
2.2节中针对RLV-T3小型可回收火箭建立了时域仿真模型,并设计了SPNNC控制器。本小节将比较SPNNC和PID 2种控制器的控制效果。SPNNC对高度的控制使用了RLV-T3飞行过程中采集到的高度、速度、加速度3种信息,PID控制器同样使用这3种信息构成串联PID控制器。SPNNC控制器的结构如图1所示,三级串联PID如图10所示。
RLV-T3小型可回收火箭对建立仿真模型存在诸多不确定因素,其中最大的不确定因素是发动机关于流量阀的推力曲线。由于实际情况的限制,RLV-T3使用的LinkPower-3发动机无法进行与RLV-T3相同状态下的出厂测试。测试获得的推力曲线仅可作为发动机基本性能评估,不可作为RLV-T3仿真模型中发动机推力关于流量阀曲线的精确模型。因此RLV-T3仿真模型中的推力曲线只能在一定范围内粗略估计。由此带来的控制负担需要由控制算法来承担。
RLV-T3仿真模型的发动机性能备选了7种不同的推力曲线,如图11所示。

图10 三级串联PID控制器结构Fig.10 Structure of series PID controller

图11 发动机推力曲线Fig.11 Thrust curves of engine
其中数据1较为接近理论推力曲线,其他6条数据曲线为在一定范围内做拉偏后的曲线。固定发动机推力曲线后保持被控对象不变,分别使用SPNNC和PID控制器进行控制,根据得到的飞行高度数据曲线可对比SPNNC和PID的控制性能。保持SPNNC和PID不变,分别使用7条推力曲线去检验2种控制器的控制效果,可检验2种控制器在复杂不确定因素下的控制性能。
推力曲线采用数据1,保持被控对象不变调整参数将2种控制器整定到最佳控制状态,得到PID的12个控制参数和SPNNC的2个控制参数如表1所示,控制效果如图12所示。由参数的数量可以看出,通过试验对控制器的参数进行整定时,SPNNC更容易整定。
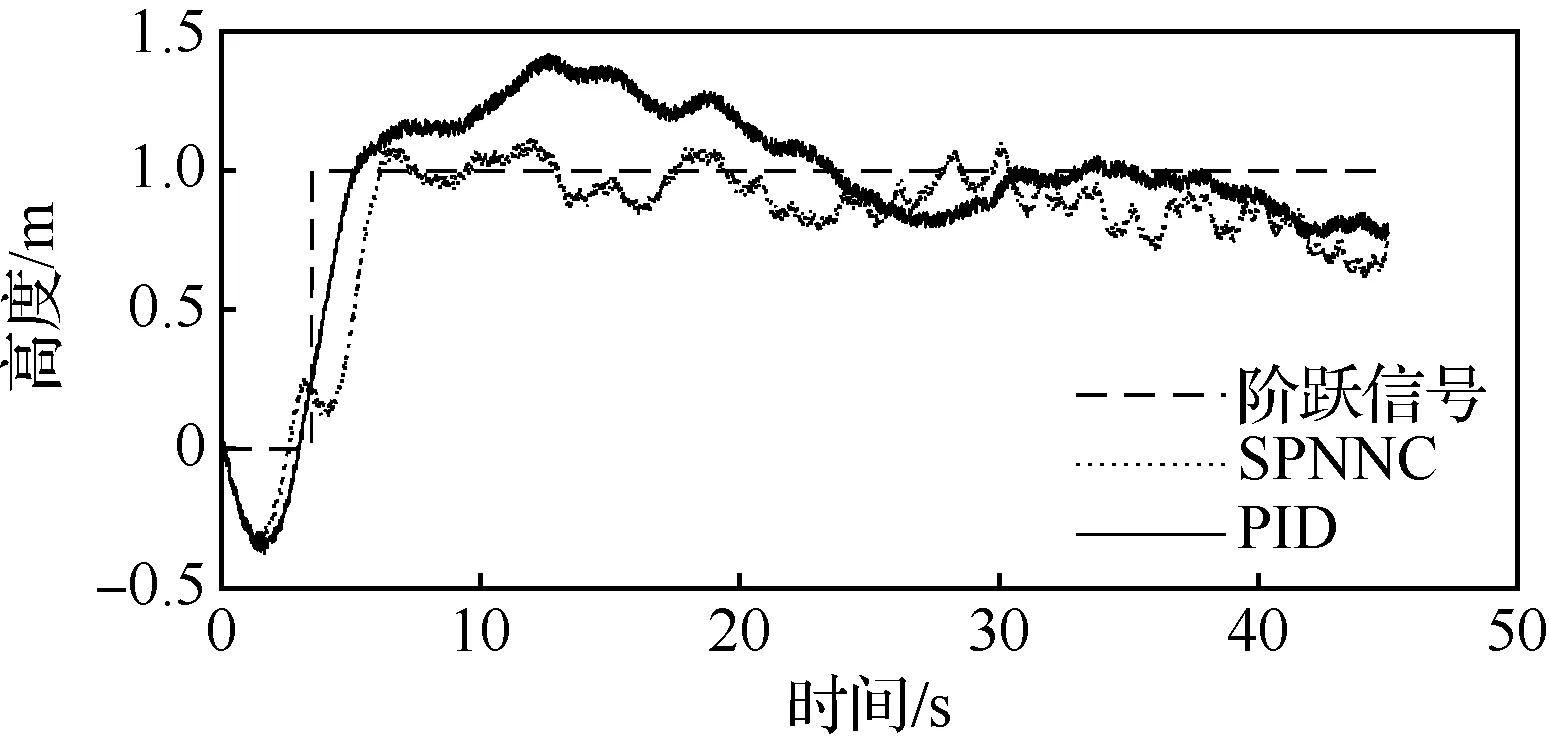
图12 两种控制器对数据1的阶跃响应Fig.12 Step response of two controllers to data 1
在保持2种控制器不变的情况下,使用7条推力曲线检验2种控制器的控制性能,获得2个控制器的7个控制性能指标。经验证2个控制器在7个推力曲线下均未出现剧烈失稳的情况。7个控制性能指标分别是稳态值、稳态误差、上升时间、峰值时间、调节时间、超调量、稳定后标准差。7个控制性能指标计算规则如下:
稳态值:选取20~45 s之间数据的均值。

表1 SPNNC和PID的控制参数Table 1 Control parameters of SPNNC and PID
稳态误差:稳态值与单位阶跃信号1的差。
上升时间:响应信号第1次达到稳态值95%的时间。
峰值时间:响应信号达到最大值时的时间。
调节时间:响应信号达到峰值后再次进入95%~105%稳态值的时间。
超调量:响应信号的最大峰值与稳态值的差同稳态值的比。
稳定后标准差:响应信号在20~45 s范围内的标准差。
计算后得到表2。其中数据1对应的图像为图12。由表2中数据可以看出,在数据1对应的推力曲线下,SPNNC和PID控制效果总体差别不是很大。PID控制器的稳态误差和上升时间都优于SPNNC,峰值时间和超调量逊于SPNNC,而稳定后标准差两者基本相同。而对于其他数据对应的推力曲线,除了数据3的稳态误差(稳态值与稳态误差直接相关)和数据5与数据7的上升时间显示出PID略优,其他所有指标均显示SPNNC优于PID,SPNNC控制器具有绝对优势。以上的数据与分析充分说明了SPNNC优越的鲁棒性与满足需求的控制精度。

表2 两种控制器对7种推力曲线的性能指标Table 2 Performance indexes of two controllers for 7 thrust curves
2.4 SPNNC对MIMO系统的控制仿真
假设存在以下系统:

(36)
对于该线性系统,可以使用式(17)进行描述和预测,因此可以使用SPNNC进行控制。为了验证其控制效果,下面通过Simulink进行仿真,其控制结构如图13所示。
其中BP神经网络采用了6输入2输出3层神经网络,被控对象模块为式(17)描述的状态转移方程和输出方程,状态预测模块为式(17)描述的预测方程。通过调整适当的参数,即可得到如下控制效果。图14为被控对象在控制器作用下对于2个阶跃信号的响应效果,图15为一个阶跃信号和一个正弦信号的响应效果。
由仿真可知,SPNNC对于式(36)描述的MIMO系统的控制响应时间较短、幅频和相频跟随特性好,可以实现解耦控制。
为了说明SPNNC对式(36)系统控制的鲁棒性,现将式(36)中被控对象的输入矩阵B做拉偏处理,即假设

(37)
式中:r=0.2,0.33,1,3,5。对于图14所示的2个参考输入,保持状态预测部分参数不变、神经网络控制器参数不变,对不同的r进行控制仿真,得到如图16所示的效果。

图13 状态预测神经网络控制算法应用于MIMO系统示例Fig.13 Example of SPNNC applied to MIMO system

图14 SPNNC对MIMO系统的控制效果Fig.14 SPNNC’s control effect in MIMO system

图15 SPNNC对MIMO系统不同信号的控制效果Fig.15 SPNNC’s control effect with different signal in MIMO system

图16 不精准被控模型下的SPNNC控制效果Fig.16 SPNNC’s effect with inaccurate plant
由图16可知,当输入矩阵发生一定幅度变化时SPNNC依然可以实现稳定控制,r越接近1控制效果越好。这种方法并不严谨,但能从一定角度反映SPNNC的鲁棒性。
进一步考察SPNNC对非线性系统的控制能力。假设实际被控对象的状态方程为

(38)
其他量不变。
对于式(38)描述的系统,首先通过泰勒展开将非线性状态方程线性化进而进行预测,可得到使用SPNNC控制器得到的控制效果如图17所示。

图17 非线性被控模型下的SPNNC控制效果Fig.17 SPNNC’s effect with nonlinear plant
由图17可见,对于非线性系统线性化之后使用状态方程进行预测依然可以实现稳定控制,只是存在微量稳态误差。这也体现了SPNNC的一个缺点,那就是控制精度略差,对此第3节将会进一步说明。
3 算法在小型可回收火箭上的验证
为了验证SPNNC的性能,使用图6中的火箭进行了多次试验验证。下面针对其中一次飞行试验进行说明。
本次飞行试验高度通道指令曲线如图17中实线所示,即分为上升、高度保持、下降、软着陆4个阶段。
上升阶段:该阶段为点火后至第18 s,在该阶段目标高度持续上升。
高度保持阶段:该阶段为18~26 s,在该阶段,箭体高度保持在6.5 m。
下降阶段:该阶段为26~37 s,在该阶段目标高度以一定速度下降。
软着陆阶段:该阶段为37 s至结束,目标高度停在0.1 m。目标高度设为0.1 m直至关机。
表3列出了本次飞行试验的状态参数和试验数据。本次飞行试验耗时为43.5 s。

表3 试验数据Table 3 Test data
图18为RLV-T3小型可回收火箭在飞行过程中高度与目标高度的关系,实际过程对指令的响应时间4 s左右,其中高度保持阶段目标高度与箭体实际高度之差最大为0.2 m,平均定高6.4 m。图19(a)为RLV-T3飞行过程中在大地坐标系下3个轴向的速度数据,其中z轴方向即为高度方向,上升阶段最大速度0.7 m/s,下降阶段最大速度0.7 m/s,着陆速度为0 m/s,无冲击。图19(b)为箭体竖直方向的运动加速度,由图中可以看出箭体在飞行过程中振动较大,除了点火瞬间,上下加速度绝对值不超过0.75 m/s2。

图18 基于SPNNC的RLV-T3飞行测试Fig.18 RLV-T3 flight test based on SPNNC


图19 箭体飞行过程中参数变化Fig.19 Parameters changing during the flight
图19(c)箭体在飞行过程中SPNNC对流量阀控制的过程。图19(d)箭体在飞行过程中两个轴向的姿态角。
本次试验场景图如图20所示。

图20 RLV-T3小型可回收火箭飞行试验Fig.20 Flight test of RLV-T3 small reusable rocket
从RLV-T3小型可回收火箭试验数据可以看出,上升阶段与下降阶段对目标高度的跟随较为平稳,高度保持阶段最大定高误差为0.2 m,最大稳态误差为0.1 m。软着陆阶段,速度曲线和加速度曲线显示着陆平稳,着陆无冲击。试验过程中SPNNC根据箭体加速度、速度、位置进行控制,动态地调整流量阀,使箭体处于动态平衡中。整个试验过程,高度控制与姿态控制解耦,箭体姿态较为平稳,通过一个小的角度抵御风的干扰。通过以上数据分析,使用SPNNC对RLV-T3的高度可以实现一定精度内的稳定控制。
4 结 论
1) RLV-T3小型可回收火箭是国内第一枚利用民间工业力量加工生产,并实现了垂直起飞、弹道飞行、空中悬停、软着陆回收全流程的火箭。对于翎客航天的VTVL技术,SPNNC起到了至关重要的作用,其极强的鲁棒性和快速响应能力保证了火箭较大变化时的控制稳定性,同时又保证了满足要求的控制精度。
2) 经过近百次的飞行试验发现,SPNNC具有很多优势和不足。SPNNC的优势包括在线学习收敛快、鲁棒性强、通用性强、可应对非线性复杂系统(可部分线性化)、可应对多变量复杂系统,参数少、整定简便。同时SPNNC也存在一些不足,例如控制精度略低、无法控制长时滞不可预测系统。对于SPNNC的低控制精度,究其原因,对未来的预测是单点预测,优化也是单点优化,下一步的研究方向将是多点预测和多点优化对SPNNC控制精度的影响。除此之外还需增加反馈校正环节,提高控制精度。
3) 对于SPNNC的稳定性,涉及神经网络、非线性系统、预测、多变量,是一个非常复杂的系统[20-22],还无法给出严密的数学证明,同时也无法给出预测步长关于被控对象的数学关系,这也是下一步的研究方向。但其控制效果已经在RLV-T3的飞行试验中得到充分展示。

