TMF本构和寿命模型:从光棒到涡轮叶片
胡晓安,石多奇,杨晓光,,*,于慧臣
1. 南昌航空大学 飞行器工程学院,南昌 330063 2. 江西省微小航空发动机重点实验室,南昌 330063 3. 北京航空航天大学 能源与动力工程学院,北京 100083 4. 中国航空发动机集团公司 北京航空材料研究院,北京 100095
涡轮叶片是航空发动机受多场热、力、化耦合载荷环境最恶劣的结构部件,其服役寿命常常决定了发动机整机大修间隔。随着发动机总增压比和涡轮前温度越来越高,涡轮叶片普遍设计为多通道空心和气膜冷却薄壁结构。由于镍基单晶/定向凝固合金在高温、长时服役条件下,能保持着优良的力学性能以及组织/化学稳定性,是目前高性能航空发动机涡轮叶片等转子零部件主要选材,且在未来相当长的时间内仍不可替代。快速的瞬态响应、长时间的高温保持,使得叶片结构经受着复杂的热机械疲劳-蠕变载荷,叶片上氧化、蠕变、疲劳损伤极为突出,呈现出强烈的位置相关性和使用相关性。此外,不可避免的几何突变结构设计引入了局部应力集中,常常在这些位置产生过早的裂纹萌生。为此,涡轮叶片材料及其结构的高温疲劳、蠕变行为受到了很大关注,相当多的学者[1-15]在该领域内进行了持续而卓有成效的研究工作,如试验方法、本构理论和模型、破坏机理和寿命预测方法等。然而,建立材料简单试样力学性能、特征模拟件和叶片之间的力学关联,并预测涡轮叶片的热机械疲劳(TMF)变形和寿命仍然是工程应用需要解决的重要问题。
TMF问题最早源于20世纪70年代,由于第3代军用涡扇发动机F100服役中热端部件热疲劳问题频发而引起了工业界的重视,美国为此还实施了热端部件结构完整性国家计划。美国电力科学研究院的公开报告指出[16],针对高压涡轮叶片的疲劳寿命估计和寿命管理主要考虑的3个方面,即热障涂层寿命、蠕变寿命和TMF寿命。此后,随着计算机控制技术的发展,20世纪80年代中后期,精确控温的TMF试验得以实现,以MarM247、PW1480等合金的TMF试验研究为早期典型代表。较早系统的TMF研究是Sehitoglu及其合作者针对1070号钢[1]、镍基高温合金MarM247[2-3]等材料所开展的试验、本构和寿命模型,并提出了著名的Sehitoglu-Neu寿命模型,考虑了疲劳、蠕变和氧化损伤。20世纪90年代,国外针对镍基高温合金的研究主要搜集在ASTM(American Society for Testing Materials)论文集[4-7],同时期北约航宇咨询组结构与材料委员会也针对航空发动机涡轮叶片材料开展了大量的TMF行为研究工作[8]。进入21世纪后,对镍基高温合金的研究仍然持续。欧洲国家为此专门成立研究组来研究TMF试验标准,2005、2011和2016年的3次TMF大会,参研单位涵盖了大量的发动机制造商、研究机构和高水平科研院校。美国方面,以与通用电气和普惠公司紧密联系的佐治亚理工大学McDowell和Neu团队针对GTD-111[9]、CM247LC[10]、PW1484[11-12]等合金的研究为主要代表。国内方面,张国栋等[13-15]较早地针对DZ125合金开展了TMF行为研究,温度范围是500~1 000 ℃和550~1 000 ℃,考虑了同相位(In-Phase, IP)、反相位(Out of Phase, OP)和135°反菱形相位(Counter Clockwise Diamond, CCD)影响。本文作者进一步研究了DZ125合金[17]TMF破坏机理。这些研究工作为国产航空发动机设计用材料数据提供了重要补充。
针对多种镍基高温合金的TMF行为研究表明[4, 18],在IP和OP TMF载荷条件下,高温合金材料的TMF寿命存在交叉,且大多数情况下都比IF寿命更短。在短寿命范围内,IP TMF寿命更短,而在长寿命范围内,正好相反。一般认为这是由于TMF载荷下,不同寿命范围内的主导破坏的损伤机理不同造成的。在其他的合金中,也有类似的现象。CM247LC DS定向凝固合金TMF寿命与IF寿命的比较表明[12],在500~950 ℃ TMF载荷下,IP和OP TMF寿命都比950 ℃等温疲劳(Isothermal Fatigue, IF)寿命低,偏差达到3~5倍,但在长寿命阶段,IP试验与等温试验趋于接近,而OP TMF比相同最高温度下的等温寿命短很多。
TMF载荷下,疲劳、蠕变、氧化等损伤交互作用与TMF相位角、载荷水平密切相关。McDowell等[19]指出,高温合金材料在TMF载荷下表现出时间相关的循环损伤,且这种损伤和环境-疲劳交互作用关联。深入理解这种损伤机理首先应该分析循环载荷对氧化过程的影响,然后再讨论氧化环境对疲劳过程的影响。循环载荷对高温合金的氧化过程具有明显的影响。Neu和Sehitoglu[18, 20]提出了一个氧化层演化的数学模型,从而识别了氧化断裂过程的两种模式,分别为I和II型循环氧化机制。对于I型氧化机制,由于高温氧化使得氧化层增长到某个临界尺寸时,氧化层将发生断裂,这个氧化层增长到临界尺寸-微观断裂过程循环发生,将产生氧化侵入。当氧化层尖峰达到某个长度时就可以假设为裂纹萌生。对于II型氧化机制,也有类似的氧化层临界厚度,但是不同之处是,发生断裂的氧化层部分地会从表面剥落,从而形成多层氧化结构。在两种氧化机制下,氧化侵入分别表现为连续的和分层的氧化层。产生这两种不同的氧化机制与温度和应变范围的相位角有关。相位角对TMF损伤机理具有决定性的作用,疲劳、蠕变和氧化损伤受到相位角的直接影响。Kupkovits[11]针对镍基定向凝固合金CM247LC在温度范围500~950 ℃ TMF微观机理研究表明,在OP TMF条件下,在试样表面上容易形成氧化尖峰,产生楔形裂纹,氧化损伤和疲劳损伤存在交互作用;而在IP TMF载荷下,由于基体与氧化层热膨胀系数的差异使得表面氧化层剥落,但不形成楔形裂纹。为了预测TMF寿命,有许多学者基于不同的角度发展了相关数学模型,可以参考Zhuang和Swansson[21]关于TMF寿命模型的综述。
单晶或定向凝固镍基合金由于其特殊的微观结构表现出各向异性力学行为。在对这类材料进行本构建模时,需要在考虑传统率相关、温度相关、循环软/硬化等基础上,还将突出各向异性和变温效应的高精建模或预测,仍是有较大挑战的工程应用问题。迄今为止,许多学者提出了基于唯象黏塑性和晶体塑性理论框架下的本构模型预测材料和结构的循环和蠕变行为[22-25]。虽然以晶体塑性为主要代表的多尺度建模方法取得了重大进展,然而,工程设计时对更为宏观的材料唯象本构模型需求更加迫切[26]。在宏观唯象模型中,统一型黏塑性模型由Prager[27]、Perzyna[28-29]、Armstrong等[30]学者提出,并经Walker[31]、 Bodner和Partom[32]、 Deseri和Mares[33]和Chaboche[23]等学者深入研究后取得突破性进展。这类模型的一般形式包含了流动方程和硬化演化方程。Chaboche[23]详尽地综述并讨论这些本构模型。
针对高温合金TMF变形行为的精确建模和预测,典型的以Manonukul等[34]、Mücke和Bernhardi[35]、Becker和Hackenberg[36]以及Shenoy等[37-38]所发表的本构模型为重要代表。Becker和Hackenberg[36]通过引入极限曲面概念针对IN718发展了一个率相关和率不相关的统一描述方法。Shenoy等[37-38]针对GTD-111定向凝固合金,分别建立了晶体塑性模型和横观各项同性黏塑性模型。这些模型都基于等温数据,获得不同温度下的材料参数,并最终利用TMF应力应变响应进行模型验证。晶体塑性模型由于计算规模大导致计算效率低,因此宏观唯象模型在结构和部件分析和设计过程中具有不可替代的作用和地位。
本文以某空心涡轮叶片及其材料DZ125为对象,建立叶片复杂瞬态应力应变分析方法,并发展叶片寿命预测方法。主要安排如下:第1部分为DZ125合金光棒和缺口TMF试验,获得不同温度循环、缺口应力集中条件下的寿命规律;第2部分为TMF损伤机理,揭示TMF裂纹萌生和扩展机制;第3部分是针对DZ125合金高温循环、蠕变发展的横观各项同性本构模型,并利用该模型完成了等温拉伸、循环、蠕变以及变温TMF等载荷下变形响应预测;第4部分为热机械疲劳寿命模型,基于等温纯疲劳、纯蠕变和纯氧化基础数据,发展了疲劳-蠕变-氧化损伤累积模型及其应力集中修正方法,预测了等温、TMF载荷下材料和特征模拟件的疲劳寿命;第5部分以某典型转速谱为输入条件,基于所发展的本构模型,预测了某涡轮叶片瞬态热机械应力应变响应;第6部分预测了涡轮叶片在某典型转速谱条件下的热机械疲劳寿命;第7部分为本文主要结论。
1 DZ125 TMF试验和寿命规律
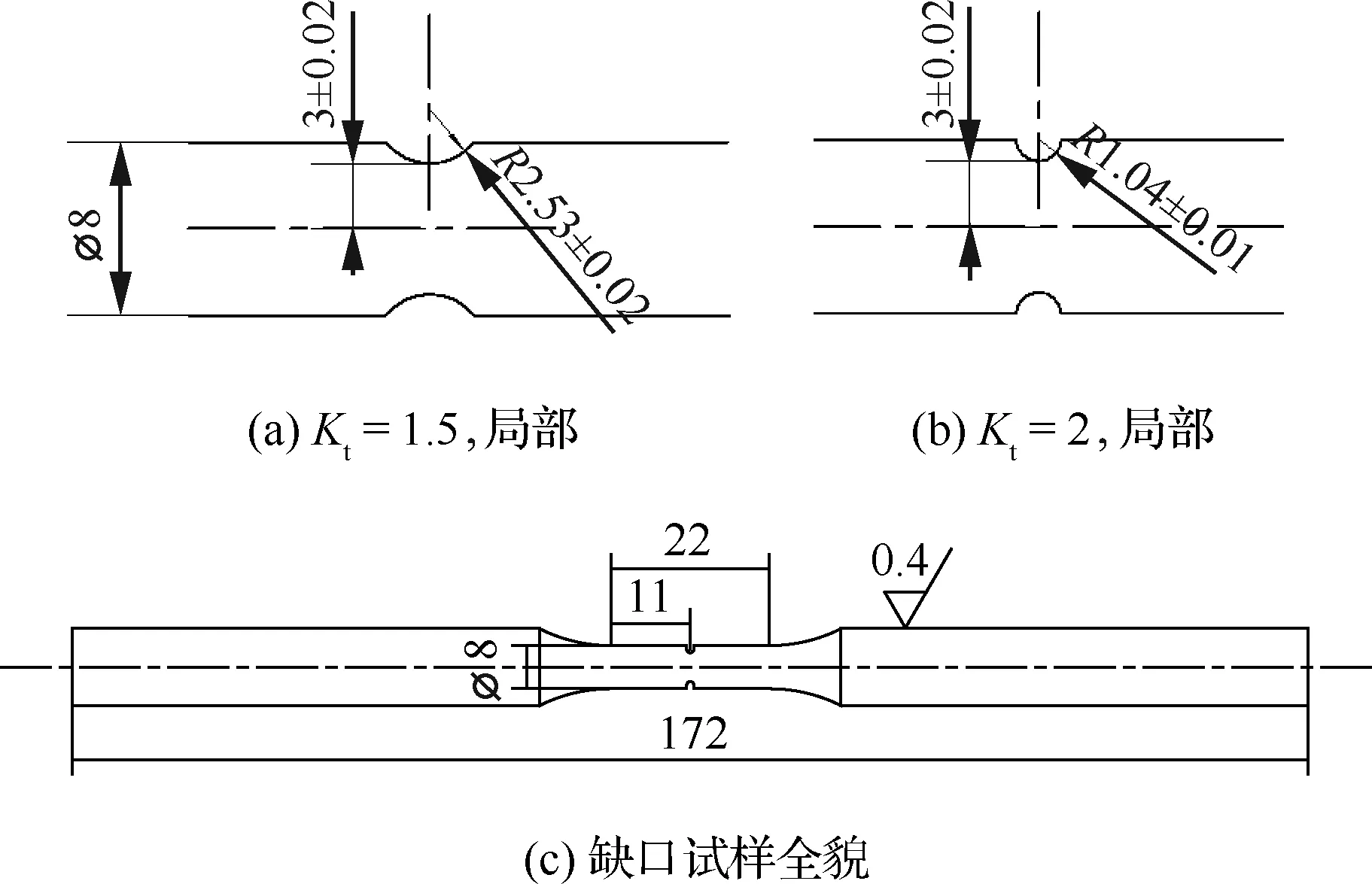
针对DZ125圆棒试样,设计了如图1所示的圆棒试样和图2所示的缺口圆棒试样,其中缺口试样设计了理论应力集中因子分别为Kt=2和Kt=1.5两种试样形式。在Instron TMF试验系统上开展试验研究。试验时,首先通过点焊方法,在试验段的中间截面和距离中间截面约10 mm上下对称点共3处焊接热电偶,如图3所示;其次,在无载荷条件下按照设定的温度范围进行感应线圈加热,并测定试样的热应变,重复进行7个循环的应变测量平均值用来补偿热应变;最后,按照总应变为机械应变和热应变之和间接实现机械应变控制。
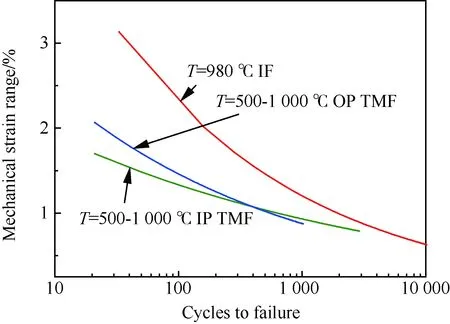
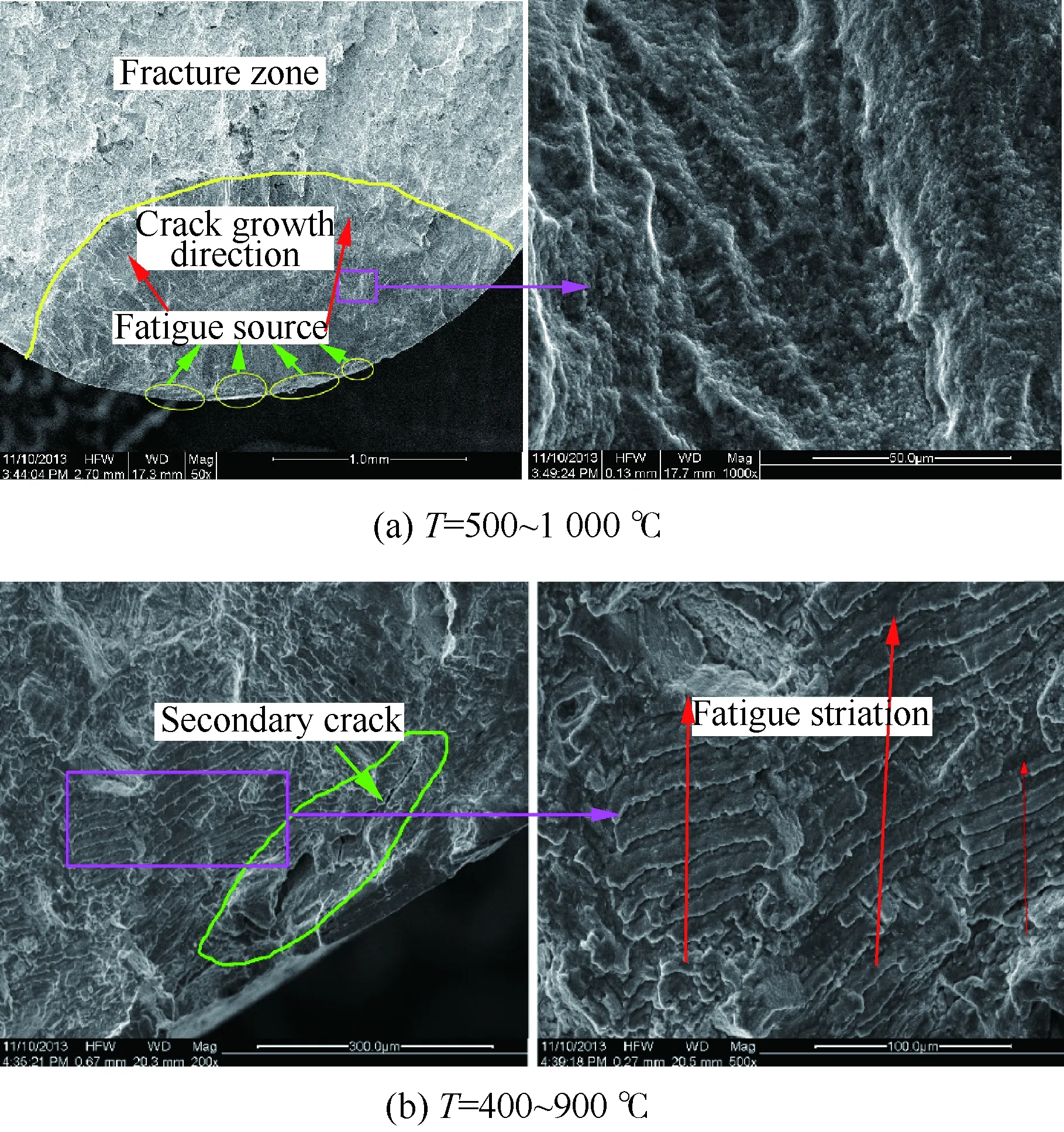
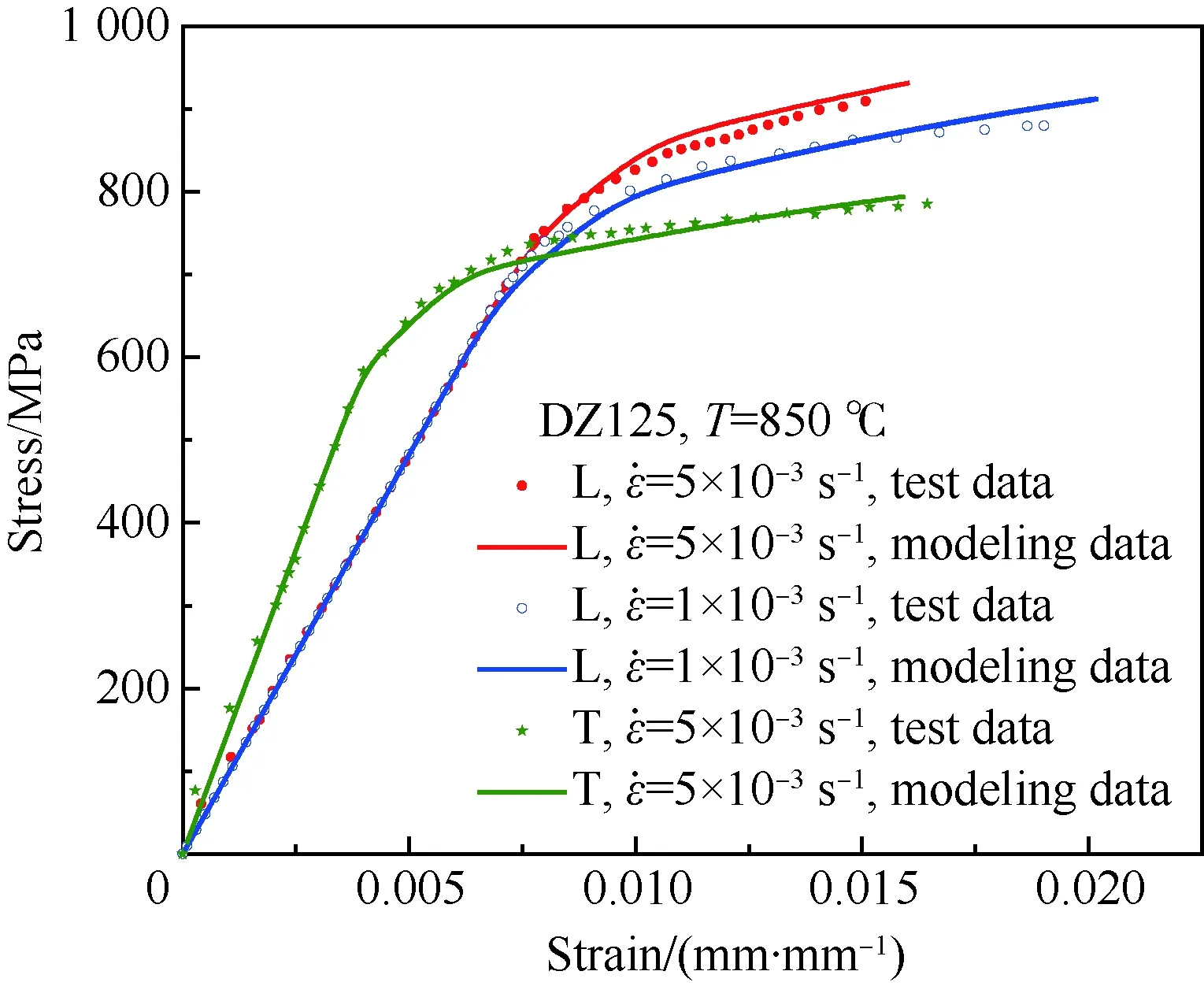
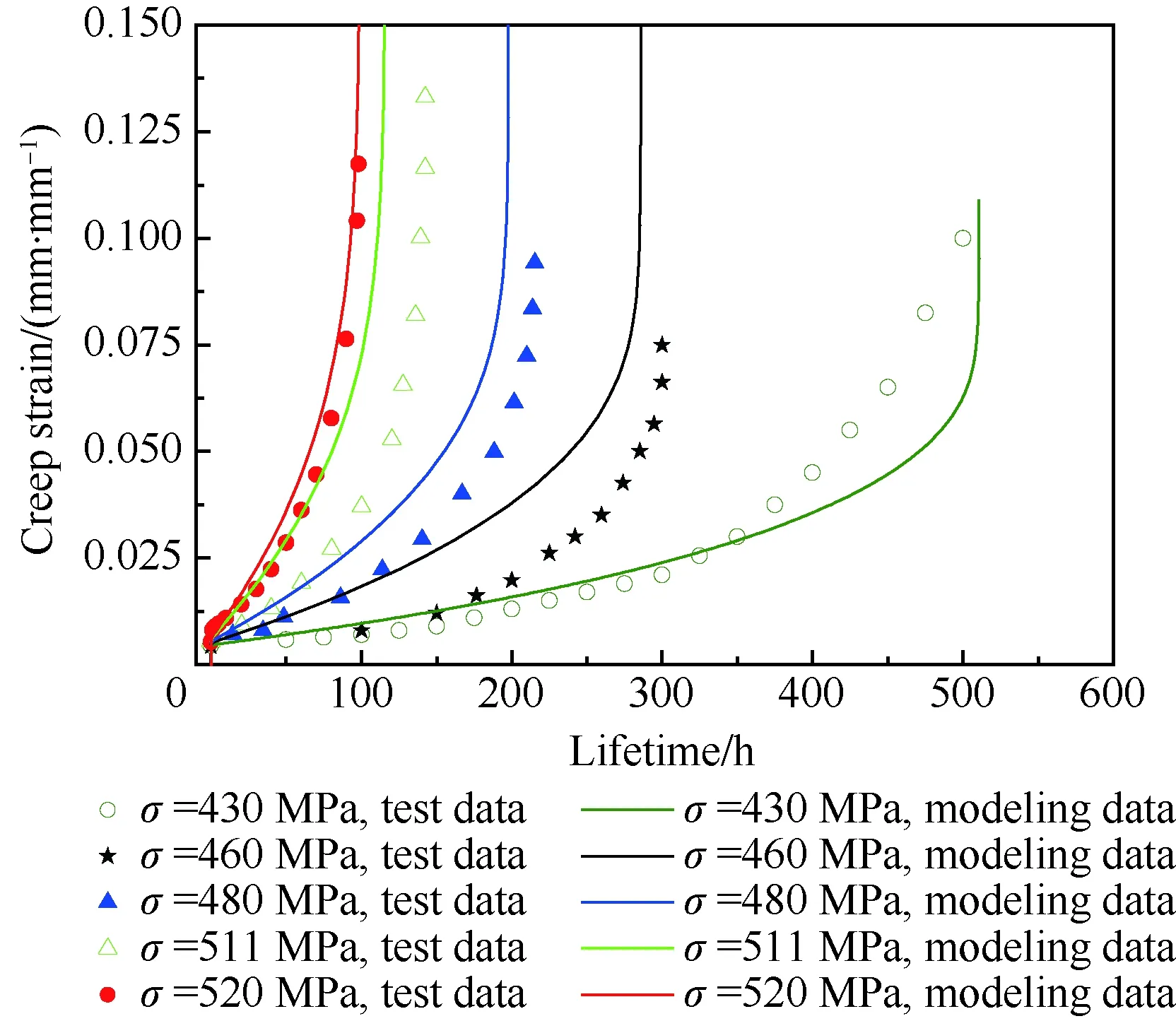
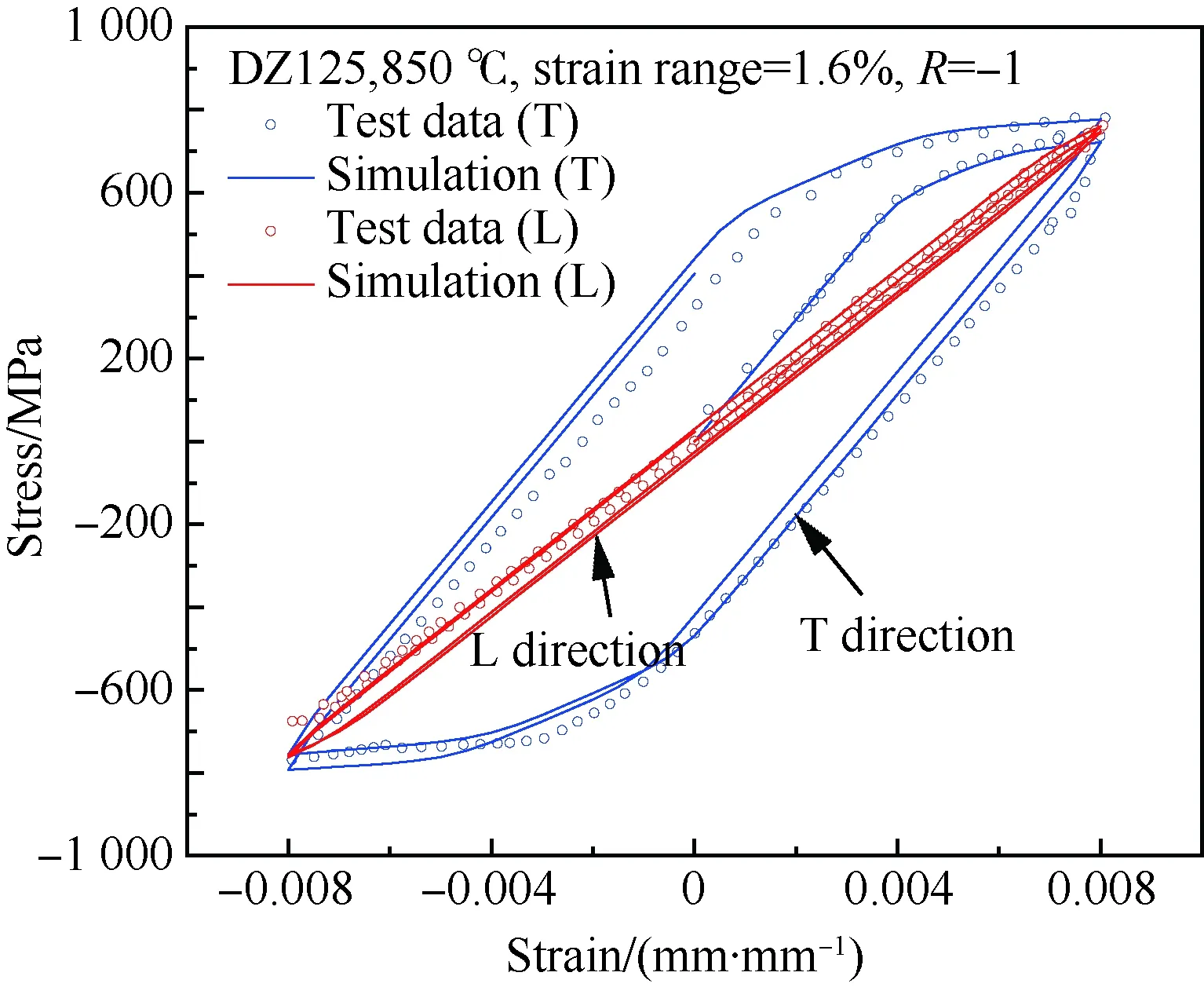
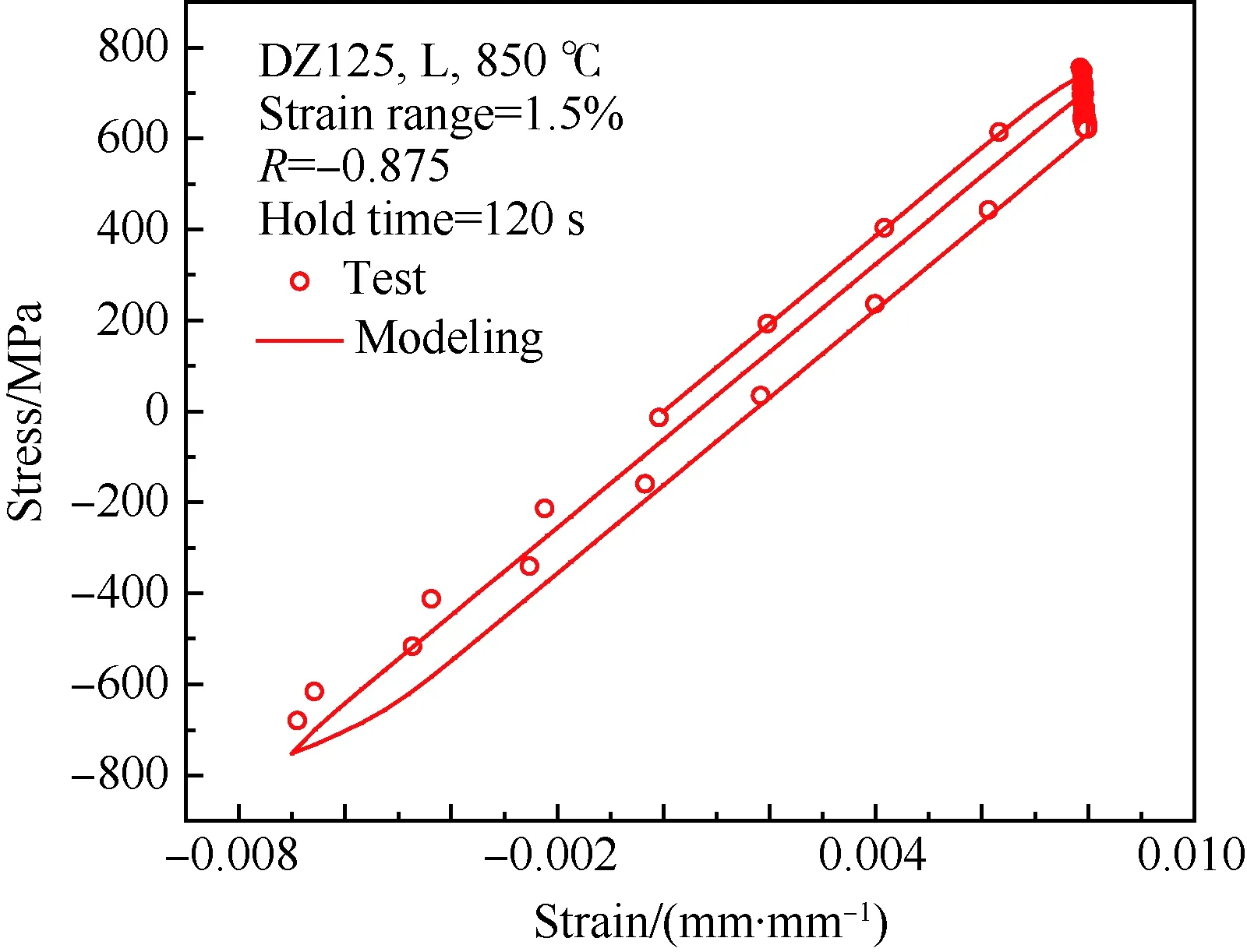
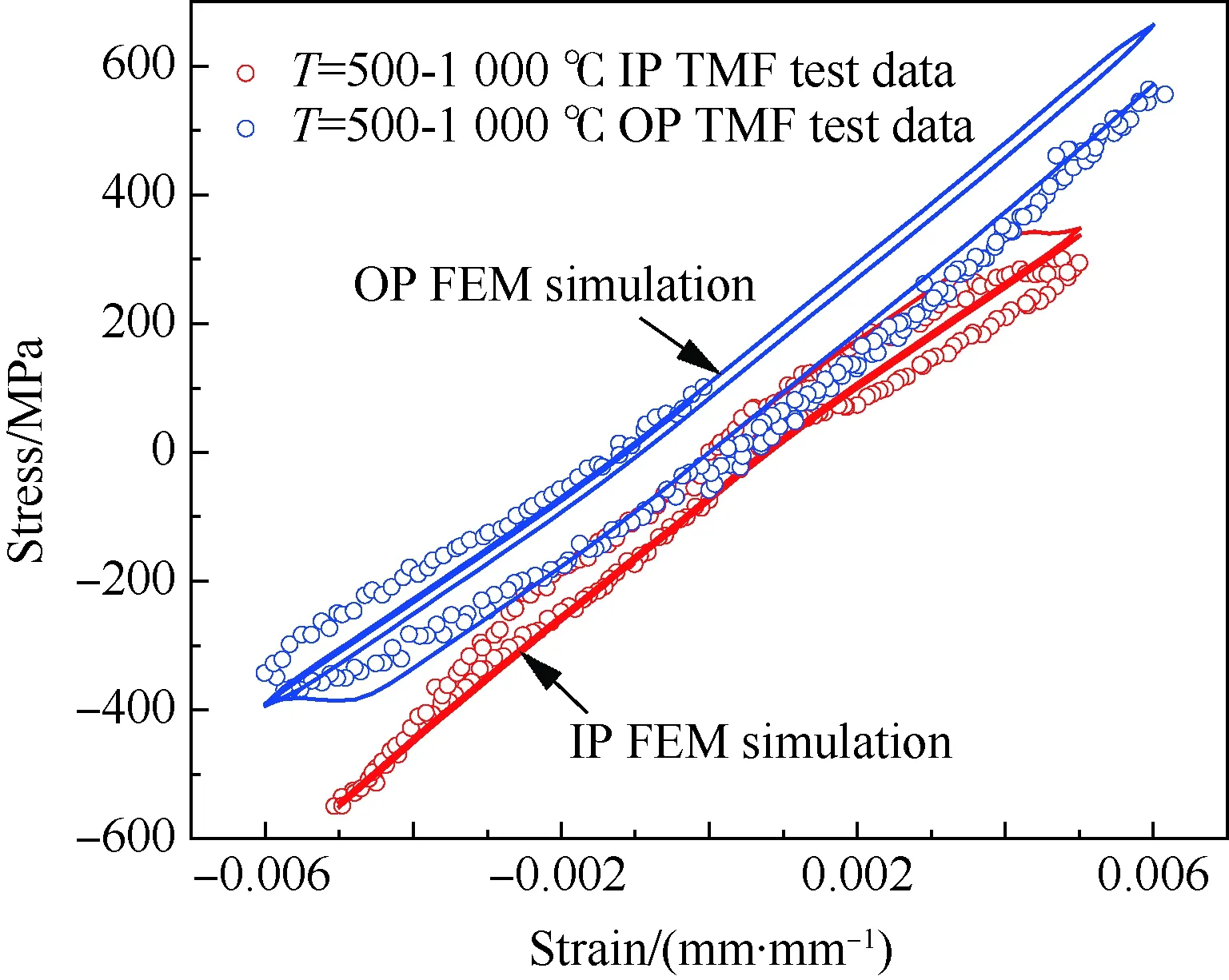
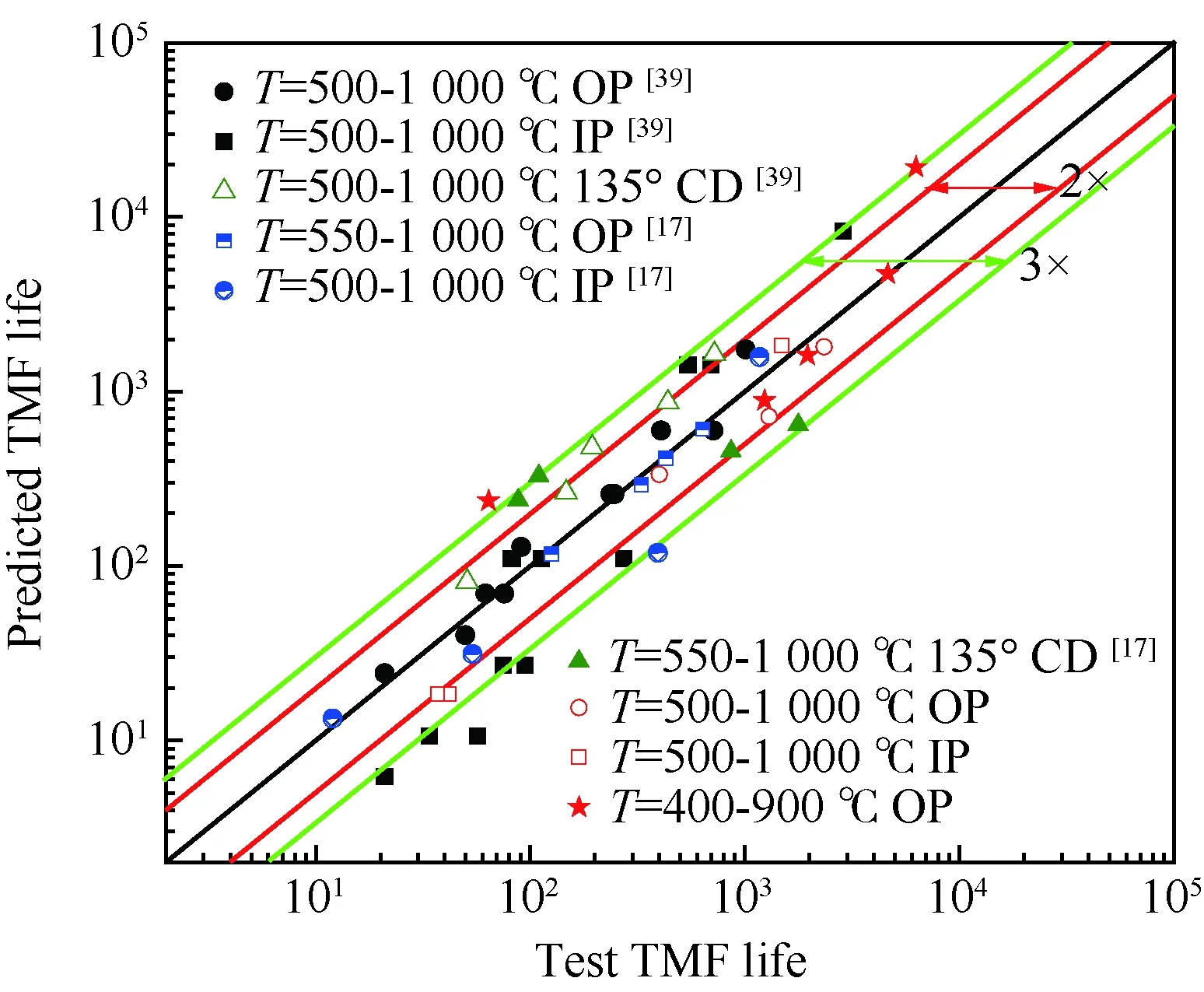
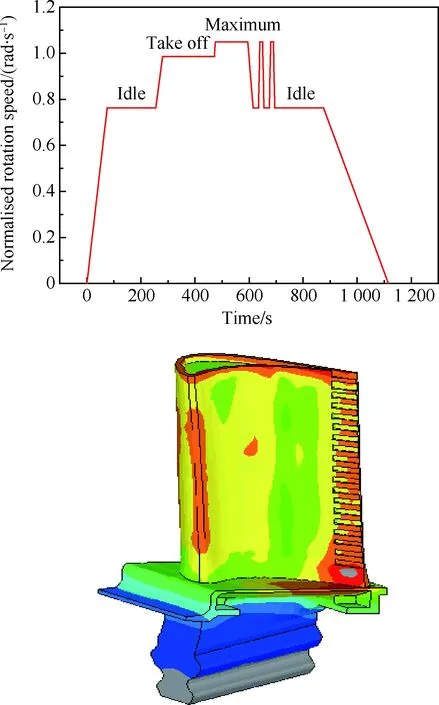
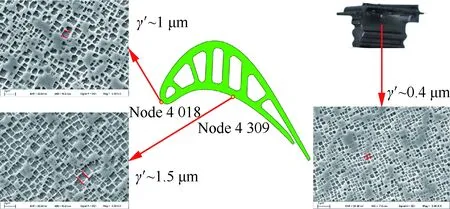
图4为光滑试样的TMF试验结果,其中部分试验数据源于公开文献[17,39]。光棒TMF试验表明:① 不同温度、相位角条件下TMF寿命分散很大,分散带约25倍;② TMF寿命短于相同最高温度下等温疲劳寿命,当机械应变相同时,最差的TMF寿命比等温疲劳(如温度T=980 ℃)下降可达50倍,比TMF循环平均时的等温疲劳寿命(如760 ℃)下降大于100倍;③ 相位角对TMF寿命影响很大。在相同温度循环下(如温度T=500~1 000 ℃),短寿命阶段,N(IP) 图1 DZ125圆棒光滑试样尺寸(单位:mm)Fig.1 Geometry size of smooth cylinder specimen manufactured by DZ125 (unit: mm) 图2 DZ125圆棒缺口试样尺寸(单位:mm)Fig.2 Geometry size of notched cylinder specimen manufactured by DZ125 (unit: mm) 图3 TMF试验系统和热电偶点焊Fig.3 TMF test facility and spot welding of thermocouples 图4 DZ125 IF和TMF寿命分布[17, 39]Fig.4 IF and TMF life distribution for DZ125[17, 39] 涡轮叶片由于结构特点,不可避免存在气膜孔、缘板过渡等应力集中。然而,考虑结构应力集中的TMF试验研究极少,Kupkovits和Neu[40]针对CM247LC定向凝固合金和Kersey等[41]针对PWA1484单晶合金研究都证实了应力集中对TMF寿命影响显著。图6为DZ125缺口试样在应力控制下,OP TMF试验后应力范围(Δσ)与寿命关系。结果表明,缺口TMF寿命相对于光棒TMF寿命减半,且随着应力集中因子的增加,缺口TMF寿命下降,从而证明了TMF寿命的缺口敏感性。通过试验研究,获得了DZ125合金的寿命规律和循环变形响应,为寿命和本构建模提供数据支撑。 图5 在500~1 000 ℃温度下DZ125 IP和OP TMF寿命曲线Fig.5 IP and OP TMF life curves for DZ125 at 500-1 000 ℃ 图6 500~1 000 ℃温度下DZ125缺口试样OP TMF寿命Fig.6 OP TMF lives of notched DZ125 specimens at 500-1 000 ℃ TMF试验结果表明,在不同的试验条件和结构形式下,TMF寿命存在很大差异。为此,本节利用SEM、EDS等手段揭示反相位TMF载荷条件温度范围和应力集中等因素作用下的破坏机理。 图7(a)和图7(b)分别为DZ125合金纵向试样在500~1 000 ℃和400~900 ℃ OP TMF载荷下的断口形貌,试验的应变范围为0.8%。从图中可以看到,在表面上存在多源裂纹萌生。对比两组试验,500~1 000 ℃条件下疲劳辉纹不明显,主要原因是疲劳裂纹扩展过程中裂纹面上产生了氧化颗粒。而在400~900 ℃ OP TMF下,裂纹扩展过程氧化轻微的多,疲劳辉纹清晰。由于TMF氧化严重,Kupkovits[11]针对CM247LC DS合金在500~950 ℃ TMF研究中,也没有观测到明显的疲劳辉纹。 图7 DZ125纵向试样在应变范围0.8%,OP TMF载荷下断口形貌Fig.7 Fracture surface of DZ125 subjected to strain range of 0.8% and OP TMF in longitudinal orientation 图8(a)和图8(b)分别为DZ125合金纵向断裂试样在500~1 000 ℃和400~900 ℃ OP TMF载荷下的纵向切片的金相图。结果表明,在500~1 000 ℃ 温度条件下,裂纹萌生源数量更多,形成楔形裂纹;而在400~900 ℃温度条件下,裂纹数量少,裂纹扩展路径上氧化少。沿着裂纹扩展的路径上,从试样表面到裂纹尖端,形成楔形裂纹,证明了氧化累积的时间相关性。在氧化聚集的位置,材料更加薄弱,更容易发生裂纹萌生与扩展。另一方面,由于裂纹首先在某些氧化物上萌生,导致该位置的“新鲜”表面不断暴露,又促进了氧化过程,使得氧化物聚集优先选择裂纹萌生的位置。因此,氧化-疲劳相互促进的交互机制,使得裂纹萌生和扩展区域聚集了大量氧化物,并导致热机械疲劳寿命与温度相关性很大。 图8 TMF后DZ125纵向试样纵向切片上裂纹萌生Fig.8 Crack initiation in longitudinal section of DZ125 subjected to TMF 图9为缺口TMF断口和纵向切片的全貌,可以清晰看到:① 缺口断口表面上产生了多源裂纹萌生和扩展;② 由于多源裂纹扩展距离几乎接近,使得断口全环都为裂纹扩展区,而瞬断区发生在试样中心。由于多源裂纹扩展长度相差不大,可以推断缺口TMF的寿命分散性都小。图10为纵向切片上缺口试样上的TMF微裂纹。结合图9(b),可以确认:① 裂纹萌生位置基本不位于缺口尖端,而是远离缺口根部的某个距离上;② 裂纹萌生后扩展并不沿着垂直于加载方向,而都是接近垂直于缺口表面的方向,即最大主应力方向;③ 主裂纹和二次裂纹时伴随着十分严重的氧化尖峰,裂纹萌生机理虽然受到应力主导,但氧化过程也加速了裂纹的萌生。 图9 σ=-200~400 MPa, Kt=1.5条件下缺口TMF裂纹萌生Fig.9 Crack initiation under notch TMF with loading condition σ=-200-400 MPa and Kt = 1.5 图10 缺口根部的微裂纹萌生Fig.10 Micro cracks initiated at notch tip 以叶片为典型代表的航空发动机结构,其设计应力水平以弹性为主。然而,由于循环、时间相关疲劳和蠕变损伤,结构表现出非线性变形演化特征。此外,对于一些应力集中和高瞬态区域,仍可能局部进入塑性。为此,发展表征材料在复杂载荷条件下本构模型是进行结构非线性变形响应精确计算的基础,对高精度寿命预测具有重要意义。对于定向凝固合金,材料表现出各向异性、率相关、温度相关、温度率相关、循环软硬化、蠕变等多种力学效应,为本构建模带来了一些难度。为了实现涡轮叶片高温变温载荷条件下循环、蠕变响应的高效计算,发展唯象层面的黏塑性模型是重要途径。为此,基于Chaboche型本构模型进行了修正和发展,在原始模型上,更加突出了变温、蠕变损伤、各向异性的表征。 Chaboche[42]采用了幂函数定义黏塑性势函数ψ,该方程最早由Malinin和Khadjinsky[43]提出,即 (1) (2) (3) 式中:σij为没有考虑蠕变损伤的应力;D为蠕变损伤,由基于经典Rabotnov-Kachanov损伤演化方程给出[44]: (4) (5) (6) (7) Chaboche型本构模型包含运动硬化X和各向同性硬化R两个内变量。在应力空间内,运动硬化代表了弹性域在主应力方向上的平移。为了描述背应力演化的多种机制特征,Chaboche及其合作者[46-47]提出了若干运动硬化的组合描述背应力演化规律 (8) (9) 在应力空间内,各向同性硬化表现为屈服面尺寸的改变。各向同性硬化是缓慢的过程,通常情况下可以利用标量形式的塑性应变来表示 (10) 式中:b和Q为材料参数;Q表示各向同性硬化量的渐近值。式(10)中,第1项通过R随着累积非弹性应变增加而增加或减少的变化,描述了循环硬化或软化现象;第2项考虑变温效应,由Benallal和Cheikh[49]首先提出。 总体上,在每个温度条件下,用28个材料参数描述DZ125合金的循环和蠕变行为。为了确定这些材料参数,需要利用等温拉伸、循环和蠕变试验后的应力和应变数据进行参数优化。为此,基于Levenberg-Marquadt非线性优化方法,采用如下步骤进行参数识别:① 利用DZ125合金的横向和纵向、不同应变率下的单调拉伸曲线,识别M11、M33、M55、K、n、k0、a1、a2、c1和c2;② 利用蠕变曲线,识别r1、r2、β1、β2、pa、pr和pk;③ 利用对称循环条件下循环应力演化曲线,确定参数m1、m2、Фs和ω;④ 利用非对称循环条件下平均应力演化曲线,识别参数b和Q。利用修正后的Chaboche模型,编制为Abaqus/Umat程序,从而实现对试样和叶片结构复杂应力应变响应的高精度数值模拟。 图11 850 ℃温度条件时DZ125纵向和横向率相关单调拉伸模拟Fig.11 Rate dependent tensile response in longitudinal and transverse direction for DZ125 at 850 ℃ 图12 850 ℃温度条件下DZ125蠕变曲线预测Fig.12 Creep deformation prediction of DZ125 at 850 ℃ 图13 850 ℃温度条件下DZ125纵向和横向迟滞环预测Fig.13 Hysteresis loop prediction of DZ125 at 850 ℃ 图14 850 ℃温度条件下DZ125保载120 s疲劳-蠕变响应预测Fig.14 Creep fatigue response prediction of DZ125 at 850 ℃ with 120 s dwell time 图15 DZ125在T=500~1 000 ℃ OP和IP TMF作用下响应预测Fig.15 OP and IP TMF response prediction of DZ125 at 500-1 000 ℃ Neu和Sehitoglu[18, 20]通过对1050号钢的TMF损伤机理的深入研究,提出了基于疲劳、蠕变和氧化3种损伤线性累积的TMF连续损伤模型。其中氧化损伤首次提出,在随后大量研究表明,该氧化损伤模型适合于镍基多晶、定向凝固和单晶合金。为此,借助于Neu-Sehitoglu模型中的氧化损伤,建立DZ125光滑试样的TMF寿命预测方法。TMF总损伤可以表示为 dt=df+dc+dox (11) 式中:dt、df、dc和dox分别为单个循环的总损伤、疲劳损伤、蠕变损伤和氧化损伤。其中,疲劳损伤采用线性损伤累积理论表示为疲劳寿命(Nf)的倒数: df=1/Nf (12) 基于Masson-Coffin提出的应变寿命模型,给出疲劳寿命方程为 (13) 式中:c和d应采用不包含蠕变和氧化损伤的纯疲劳数据拟合得到;Δεmech为机械应变范围。对于DZ125,可用760 ℃的低循环疲劳数据确定参数c和d,分别为0.0407 3和-0.130 7。 图12针对蠕变变形模拟结果表明,修正的Chaboche本构模型可以较好地预测3个阶段的蠕变变形及其对应损伤。当蠕变损伤达到1时,试样将发生蠕变断裂。因此,可以通过有限元计算直接得到材料或结构的蠕变损伤(Umat程序状态变量)代入式(11)。此外,当不采用本构模型时,也可以通过Larson-Miller模型,得到给定温度T、应力σ作用下的蠕变断裂时间tr(σ,T)。在一定时间dt作用下,利用线性累积原理计算蠕变损伤,即 ddc=dt/tr(σ,T) (14) 式中:tr(σ,T)通过Larson-Miller模型写成 lgtr(σ,T)=b0+b1/T+b2x/T+ b3x2/T+b4x3/T (15) 式中:x=lgσ;b0、b1、b2、b3和b4均为材料参数,如表1所示。典型的TMF循环作用下,温度和载荷都是时间的函数,于是单个循环的蠕变损伤可以通过积分得到 (16) 式中:tc为循环时间。 表1 DZ125 Larson-Miller参数Table 1 Larson-Miller parameters of DZ125 Neu和Sehitoglu[18, 20]基于裂纹尖端氧化-开裂循环机理定义了氧化损伤为 (17) (18) 式中: (19) (20) (21) (22) 对于镍基合金来说,一类材料的氧化性能具有相似性,通常遵循抛物线氧化增长规律。因此,针对多晶Mar-M247、定向凝固GTD-111和单晶PW1480/1484的TMF寿命预测研究中,都将β设定为1.5,而其他参数参考Mar-M247材料在微观上的观测结果。对于DZ125合金,假设氧化损伤中应变范围的指数项与氧化损伤演化规律一致,利用一组500~1 000 ℃条件下的OP TMF数据拟合得到b/β+1为5.3。氧化损伤中其他参数数值仍参考Mar-M247材料,如表2所示。 表1、表2及纯疲劳参数共16个参数描述了DZ125合金纵向方向的TMF寿命行为,预测结果如图16所示。结果表明,在52个数据点中,有47个数据落于3倍分散带以内,其中35个数据点落于2倍分散带以内。因此,所发展的模型适于不同相位、不同温度范围的TMF寿命预测。 表2 DZ125氧化损伤参数Table 2 Oxidation damage parameters of DZ125 图16 DZ125 TMF寿命预测Fig.16 Life prediction of DZ125 under TMF 王井科[50]、Moore[51]等针对定向凝固合金等温缺口疲劳的研究表明,缺口应力集中系数和名义应力均有很大的作用。CM247LC定向凝固合金、PWA1484单晶合金的缺口TMF试验结果证实了应力集中对TMF寿命影响显著。图6则进一步地证实了缺口应力集中对DZ125 TMF寿命的影响。针对DZ125等温缺口疲劳的寿命建模研究表明,可以采用考虑了应力集中因子的名义应力模型实现光滑试样和缺口试样寿命联系,即 (23) 式中:参数m代表了材料在疲劳载荷下的缺口敏感程度;此处a、b为光棒试样TMF疲劳常数。文献[52]的分析表明,对于镍基合金其数值范围是0.2~0.3,且DZ125材料高温疲劳参数m为0.25。利用图6中光棒OP TMF试验得到了应力-寿命关系拟合得到: (24) 于是当考虑缺口OP TMF时,基于等温疲劳缺口敏感系数,修正模型式(24)得到寿命模型为 (25) 利用式(25),预测得到DZ125光棒和缺口TMF寿命如图17所示,预测寿命分散为2倍。当Kt=1时,式(25)退化为光滑试样情况。 图17 基于名义应力法的DZ125缺口TMF寿命预测Fig.17 Notched TMF life prediction of DZ125 based on nominal stress method 对结构进行应力应变响应计算是强度和寿命评价的前提。图18为某涡轮叶片的实物照片和有限元网格。由于叶片上气膜孔等结构细节导致网格模型复杂,为气热分析带来难度,为此对叶片模型进行了简化,采用八节点六面体单元划分得到图18所示的有限元模型。 图19为高压转子物理转速谱和叶片温度场。载荷谱包含了启动、慢车、起飞、最大等状态,累积时间为1 115 s。在最大状态和慢车之间循环3次,模拟油门杆频繁操作带来的瞬态效应。图19还显示了某个时间节点下的温度分布。在进行瞬态热机械应力分析时,由若干组不同状态下温度场文件组成温度边界。为了约束叶片的刚体位移,在图18所示的叶片榫头齿面上约束了法向和轴向位移。 图18 涡轮叶片实物和有限元网格Fig.18 Photo and finite element method of turbine blade 图19 高压转子物理转速谱和涡轮叶片温度场Fig.19 Physical rotational speed profile of high pressure rotor and turbine blade temperature field 在发动机巡航等稳定状态下,涡轮叶片典型地发生蠕变,使得叶片微观组织退化(如γ′粗化或筏化),并在宏观上产生不可恢复的蠕变伸长。例如,PW公司公司JT8D涡扇发动机大修标准中就规定高压一级涡轮叶片伸长量不能超过0.28 mm(0.011 inch),否则涡轮叶片将作判废处理而不能继续服役。因此,对叶片进行蠕变分析是进行强度和寿命评价的重要手段,且蠕变损伤计算结果还将用于TMF寿命预测。将图19中载荷谱的最大状态的保持时间设定为1 000 h,利用Abaqus/Umat程序计算叶片的变形,考察叶尖蠕变损伤和变形。 图20为1 000 h蠕变损伤云图以及1/2叶高上前缘和叶盆上两个较大蠕变损伤位置上1 000 h蠕变损伤演化情况。从图中结果表明,整个叶片上1 000 h的最大蠕变损伤为0.166。若采用线性累积损伤理论,假设1个飞行循环为1 h,则单个循环的损伤贡献约为0.001 66,若疲劳损伤为0,则预计的循环数约为6 000个循环或纯蠕变寿命约为6 000 h。图21为叶片服役300 h后的微观组织。由于伸根处温度较低,可以假设为该处微观组织与新叶片一致,因此初始γ′尺寸约为0.4 μm。经过300 h服役后,前缘4018节点和叶盆4 309节点处γ′尺寸发生了粗化,分别为1 μm和1.5 μm。微观损伤与图20中计算结果趋势一致。 图20 叶片蠕变损伤分布及演化Fig.20 Distribution and evolution of blade creep damage 图22是叶尖伸长量计算结果表明:① 叶尖前缘的蠕变位移最大,这是前缘温度高导致的,其次为叶背(吸力面),主要原因是涡轮叶片在离心弯矩作用下,拉伸的弯曲应力与离心拉伸应力叠加作用形成的;② 300 h保持条件下,前缘位置伸长量为0.218 mm,而在1 000 h保持条件下,伸长量增加到0.298 mm。 图21 某涡轮叶片300 h服役后3个位置处微观组织对比Fig.21 Comparison of local microstructures in three locations for a real blade after 300 h tests 图22 叶尖蠕变伸长量计算结果Fig.22 Creep elongation calculation at blade tip 由于横向裂纹是叶身最严重的损伤模式,为此主要考察径向应力和应变。图23显示了1/2叶高横截面上所考察的节点和截面上的最大状态时的径向应力分布。可以看到,在外表面上呈现为压应力状态,而在内冷却通道上以拉伸为主。因此,叶片上的温度分布对局部应力影响很大。 图24为1/2叶高前缘位置3 699号节点的径向应力与温度、径向应变与温度的关系。计算结果表明:① 温度和应力/应变的关系几乎是相同的;② 发动机从慢车到起飞或最大状态,应变范围和温度都变化快,其中温度通常从750 K(约480 ℃)变化到1 200 K(约930 ℃)。目前,公开发表的TMF试验数据多数对应着最低温度在450 ℃附近,最高温度约900~1 050 ℃,TMF试验的最低温度并不采用发动机启动时的室温状态,而选用慢车时的叶片温度;③ 温度-应变为反时针的菱形TMF循环;④ 应变范围约为0.25%,且尤其需要说明的是,中间状态时对应着应变大约为-0.225%。因此,只进行稳态应变计算时,基于0-Max-0假设获得的应变范围比瞬态应变范围低11%,考虑到疲劳寿命与应变范围成指数关系,单纯的疲劳寿命估计将相差很大,且偏于危险。 图23 叶片50%叶高横截面上的节点和径向应力Fig.23 Node and radial stress in transverse section of blade at 50% height 图24 前缘3 699号节点上的TMF循环Fig.24 TMF cycles at leading edge (Node 3 699) 图25为所考察的9个节点的温度-机械应变关系。计算结果表明,3 942、3 864和3 705节点处温度-应变相位更接近IP;对于压力面上的3 740和吸力面上的3 859节点,温度-应变循环为OP; 3 699、3 768和3 911节点则经历了CCD TMF循环;尾缘位置的3 987节点则经历了CDTMF循环。叶片上机械应变的组成包含了离心拉伸应力、离心弯曲应力和热应力。在这3部分应力中,离心应力恒为正,与叶片质量、横截面积和转速相关。外表面上的热应力在启动时受压,但在停车过程中转为拉伸,内冷却通道上则相反;离心弯曲应力大致为叶背为正,叶盆为负。由于叶片上温度与转速同步,因而应力向压方向增加时,接近反相位或反时针菱形载荷谱;当应力向拉伸方向发展时,接近IP或顺时针菱形载荷谱。对于涡轮叶片前缘,由于热应力很大,离心拉伸应力不足以在绝对值上抵消热应力,使得叶片经历反相位载荷谱。对于涡轮叶片内冷却通道,由于温度较低使得热应力为拉伸,正向叠加离心拉伸应力,使得温度-机械应力相位接近IP。因此,不同位置处叶片机械应变-温度相位差异很大,主导了局部失效模式和使用寿命。 图25 不同节点处TMF循环Fig.25 TMF cycles at different nodes 以涡轮叶片前缘3 699号节点,进行在图19所示转速谱下的TMF寿命预测。从图18可以看到,前缘广泛地存在气膜孔,假设应力集中因子为1.5。对于3 699号节点,最小应变为-0.229%,最大应变为0.020 9%,应变范围为0.24%。根据式(25)缺口敏感性,修正考虑了1.5倍应力集中因子后的应变范围是0.27%。单个循环的疲劳、蠕变、氧化损伤分别计算如下:根据式(12),计算得到单个循环的疲劳损伤df为9.63×10-10;根据叶片稳态计算结果,节点1 000 h的蠕变损伤为0.07,假设1个起落巡航1 h,则单个载荷循环的蠕变损伤dc为7×10-5;节点温度范围为527~1 020 ℃,慢车到中间状态35 s,应变率为7.71×10-5s-1,根据式(18)计算得到单个载荷循环氧化损伤dox为8.29×10-5。 对应载荷谱中包含的3个慢车-最大循环,因此疲劳、蠕变和氧化损伤分别为2.89×10-9、7×10-5、2.49×10-4,根据式(11)线性损伤累积原理,单个载荷谱总损伤为3.19×10-4,从而叶片前缘位置3 699号节点的低循环疲劳寿命为3 135。 1) 最高温度一定时,DZ125 TMF寿命比等温疲劳寿命相差3~4倍,且与相位相关。在短寿命区域,IP TMF寿命更短;但在长寿命区域,反相位TMF寿命更短。缺口使得DZ125合金TMF寿命下降,且随着缺口应力集中因子的增加,TMF寿命降低。 2) 光棒和缺口TMF试验条件下,表面氧化的作用,导致多源裂纹萌生。针对光滑试样:相对于400~900 ℃ OP TMF,在更高的500~1 000 ℃温度下,更容易形成含氧化尖峰的楔形裂纹。针对缺口试样,主裂纹萌生位置与最大主应力吻合,且存在显著的疲劳-氧化交互作用。 3) 采用Chaboche本构模型时,添加各向异性矩阵可以用于对定向凝固不同取向的应力应变行为的表征。对模型进行变温考虑和参数进行温度插值后,则进一步应用于TMF变温情况。通过引入蠕变损伤来修正等效应力,则将只能模拟第1阶段和第2阶段蠕变的Chaboche模型扩展到可以模拟第3阶段蠕变变形。 4) 借助于Neu-Sehitoglu模型(尤其氧化损伤模型),预测了考虑不同温度范围、相位角的TMF寿命。缺口对TMF寿命的影响存在缺口对IF寿命相当水平的缺口敏感性,因此借助于等温缺口疲劳寿命模型预测了TMF缺口寿命。 5) 涡轮叶片在瞬态载荷下不同区域内表现为不同相位的TMF载荷,在涡轮叶片表面上,更倾向于反相位或反时针菱形TMF载荷,而在内部更容易激发IP TMF载荷。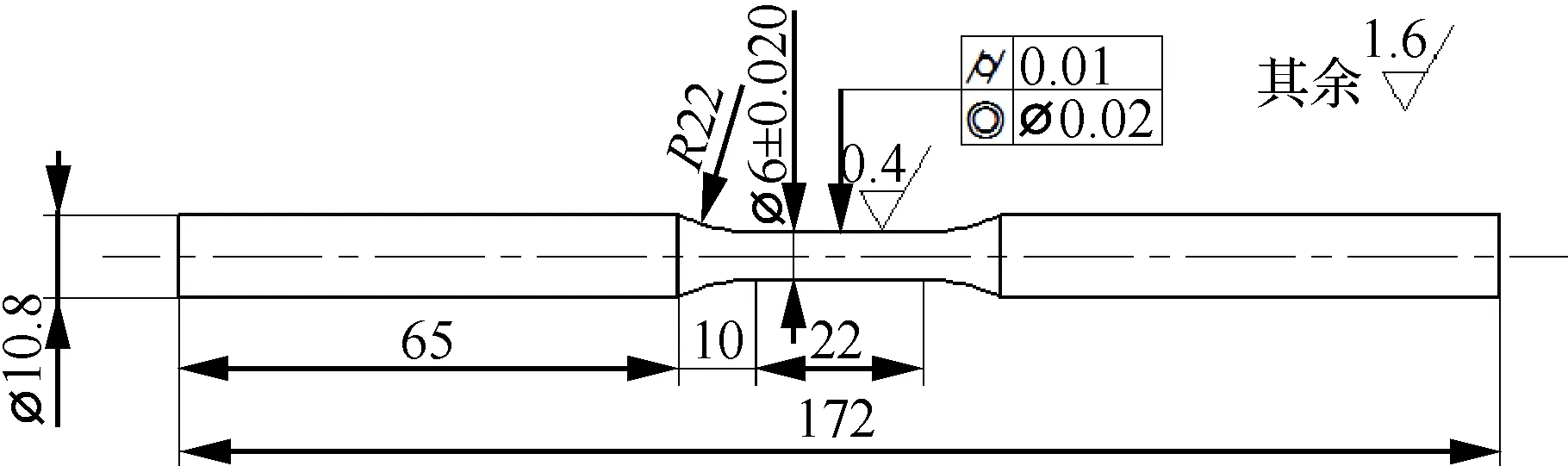



2 DZ125 TMF损伤机理
2.1 反相位光棒试样TMF裂纹萌生机制

2.2 缺口试样TMF裂纹萌生机理


3 横观各向同性黏塑性本构模型


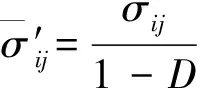
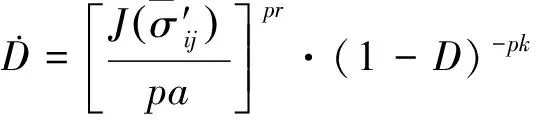
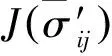

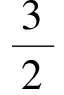

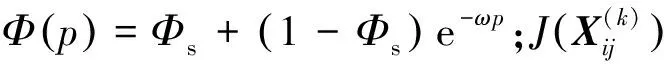

4 DZ125热机械疲劳寿命预测
4.1 光滑试样TMF寿命预测

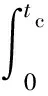

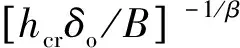

4.2 缺口试样TMF寿命预测
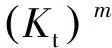

5 某涡轮叶片复杂变形模拟
5.1 叶片网格和边界条件

5.2 涡轮叶片蠕变分析结果

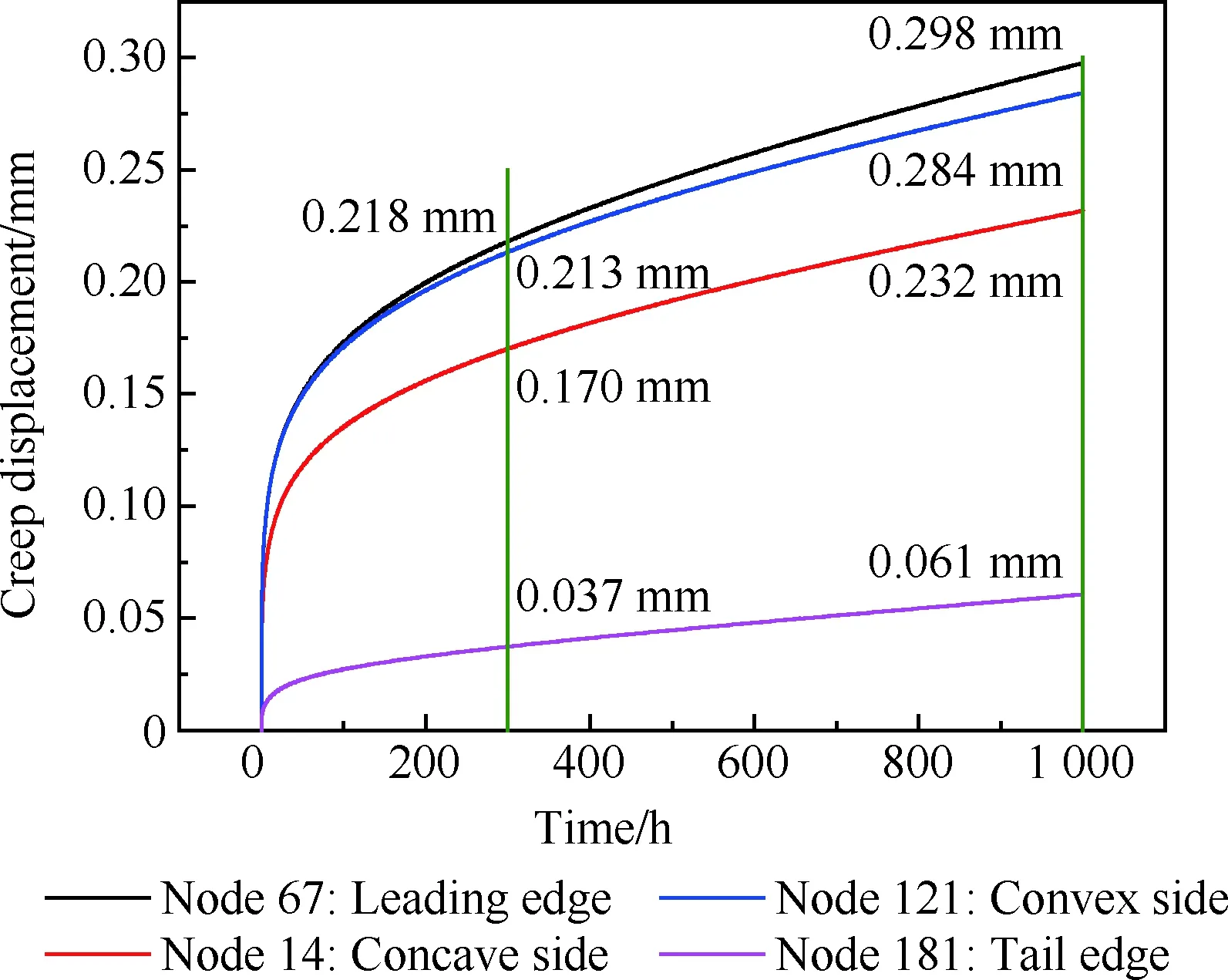
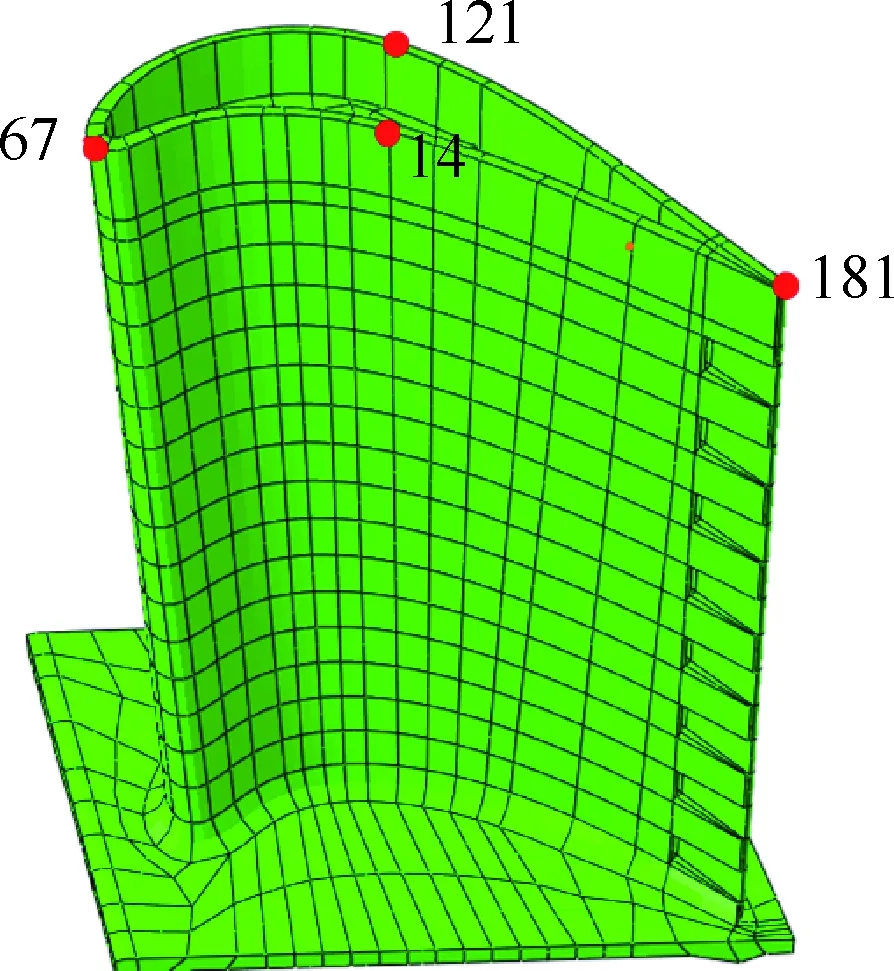
5.3 涡轮叶片热机械应力应变分析结果
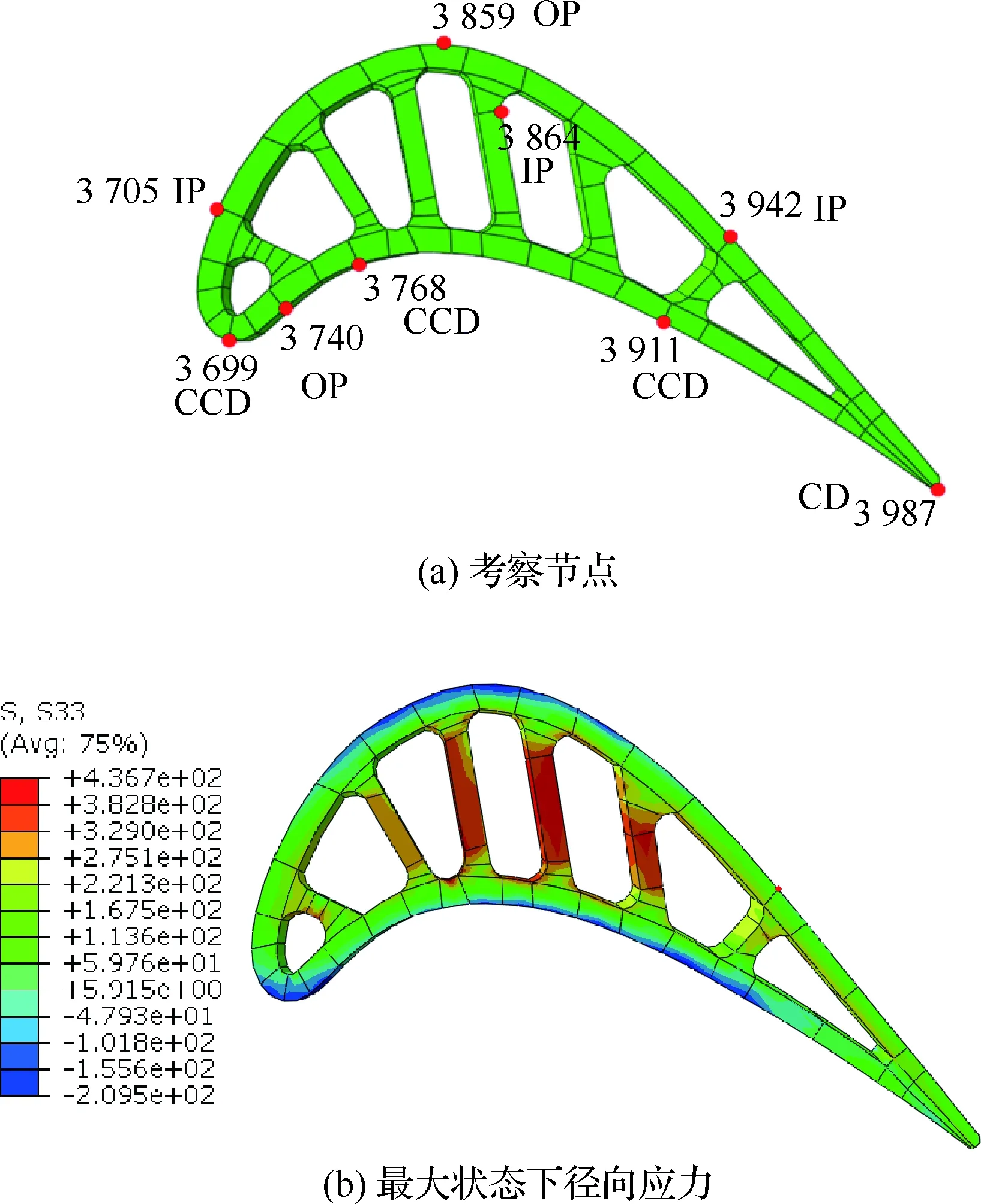


6 某涡轮叶片典型位置TMF寿命预测
7 结 论

