关于提升风电就地消纳的多介质储能系统容量的优化配置

，，，

(东北电力大学 电气工程学院，吉林 吉林 132012)

0 引 言

在风电厂的运行中，风电渗透率呈现不断增加的趋势。由于存在间歇性等特征导致其对电力系统的运行带来了较大的挑战，而就地消纳则成为处理问题的重要手段[1]。因此，探究储能容量的配置，对系统稳定运行产生巨大影响。

1 风电不平衡功率DFT分解计算

风电不平衡功率的分解中，需要通过DFT分解的方式，获取频域信息，之后确定低频截止频率f1以及高频截止频率fH，在不同的频段内，对系统进行补偿[2]。在不平衡功率的计算中，储能系统需要对风电功率开展预测，假定存在输出功率，t时刻输出功率为Pim(t)，则不平衡功率如公式(1)所示。

Pim(t)=Pw(t)-Ps(t)

(1)

通过傅里叶变换，对不平衡功率进行分析，其频率分布如公式(2)所示：

(2)

式中，N表示数据总数。对反傅里叶变换进行分析，如公式(3)所示。

(3)

在不平衡功率的分解方面，需要将其分为低频、中频和高频阶段，之后对不同的阶段采用差异性的补偿。低频应用蓄电池补偿，中频应用超级电容器补偿，高频应用同步发电机补偿[3]。

2 混合储能容量分析

在系统分析中，需要确定傅里叶变换结果，以此来确定储能容量，在计算过程中，首先通过补偿功率域值来分析T时间段的累计能量[4]。如公式(4)所示。

(4)

式中,T表示不平衡功率的时间周期，之后对额定容量进行分析，如公式(5)所示。

(5)

通过分析发现，上限制SOCup的数值为1，下限值SOClow的数值为0.3，因此，发现混合储能容量相对较高。对初始荷电状态进行分析，如公式(6)所示。

(6)

通过上述公式，可以确定初始荷电状态，且可以实现反馈控制。

3 计算截止频率

截止频率的计算中，为了保证不平衡功率的补偿，需要确定最为合适的混合储能容量配置，并且确定不平衡功率的截止高频率以及低频率。在高频率fH的计算中，确定偏差最大值Δfmax，同时采用同步发电机实行补偿，本次研究采用功率谱密度的方式来计算电网频率偏差，首先应用DFT的方式处理不平衡功率，之后确定偏差功率谱密度PSD，模型如图1所示。

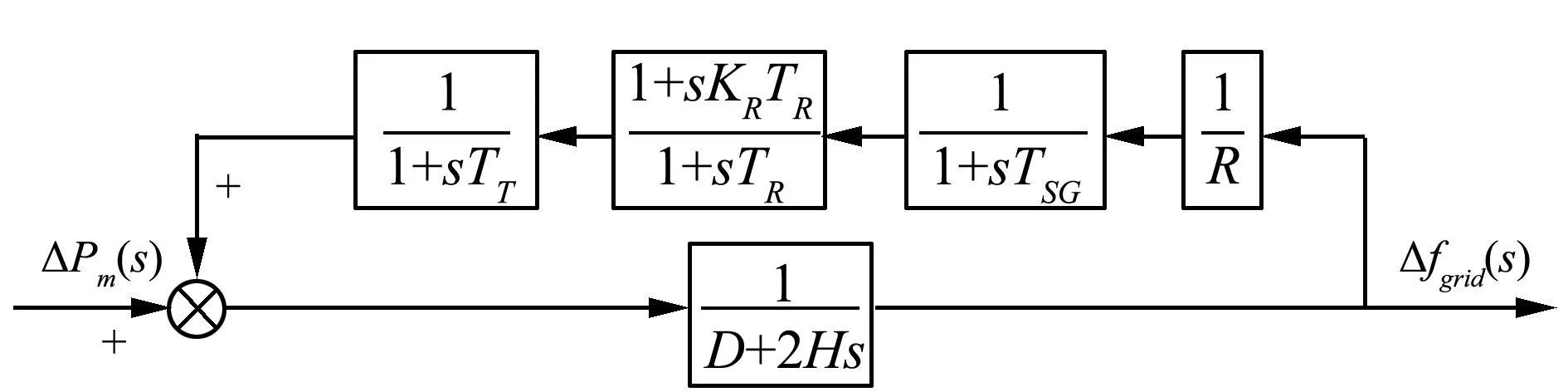
图1 频率响应模型图

在上述模型中，TSG为0.08s，参数R为0.05，常数Kr为0.3，时间常数TR为0.3s，阻尼系数D的数值为0.1，惯性常数H的数值为5s，对上述数据进行计算，如公式(7)所示。

(7)

经过对PSD的计算，可以在变换的情况下，确定时域值Δfgrid(t)。最后通过对比电网频率偏差以及最大值的情况下，可以确定系统是否满足要求，但是该方法模式下，不平衡功率频带将更为狭窄，且容量大小要求会逐渐降低。

在低频截止频率的计算中，运用梯度搜寻的方式来获得最优解[5]，输入不平衡功率，假设f1与fH相等，通过带通滤波器来处理不平衡功率，如果更新后的低频年耗降低，则证明最优解，且可以确定储能容量。

4 以利润最大为目标的机会约束规划储能运行策略模型构建及算法流程

4.1 模型的构建

这次研究建立机会约束模型，如公式(8)所示。

(8)

式中，X表示常规变量；α和β表示置信水平；p表示约束条件。ζ表示随机变量，经过分析，可以获得储能方程。

之后建立机会约束规划模型，电价是随机变量，在模型中，建立如公式(9)模型。

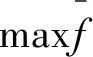
(9)

式中，C表示预测电价；△C表示电价预测误差；P表示功率；Δt表示时间间隔；η表示放电效率，文中在分析中，将遗传算法以及蒙特卡罗模拟结合起来，输入初始值，检验可行性。

4.2 算法流程

这次研究算法流程如下：(1)运用DFT分解获取频域信息；(2)利用功率源，确定最优补偿，且确定时域以及选择标准；(3)确定最优的容量值；(4)选择蓄电池、同步发电机以及超级电容器来确定补偿，最终确定储能容量；(5)建立容量值合理性约束模型，选择分段点；(6)建立机会约束模型，确定限值范围。

5 算例分析

在系统测试中，选择某风电场进行52周的测试，结果如下：

5.1 储能容量分析

对某风带南昌的分析中，发现fH=0.016 Hz，对其偏差持续时间进行分析，结果如图2所示。

图2 某风电场频率偏差持续时间图

通过分析发现，在应用混合储能系统的情况下，不平衡功率在0.016以下，且偏差率达到0.23%，处于合理的范围内。而在未应用系统的情况下，则超过合理范围，确定了该系统的可行性。

5.2 置信水平对函数的影响

概述约束问题与条件中，与置信水平存在显著的关联性，在置信水平为1的情况下，需要制定严格的约束条件，置信水平如图3所示。

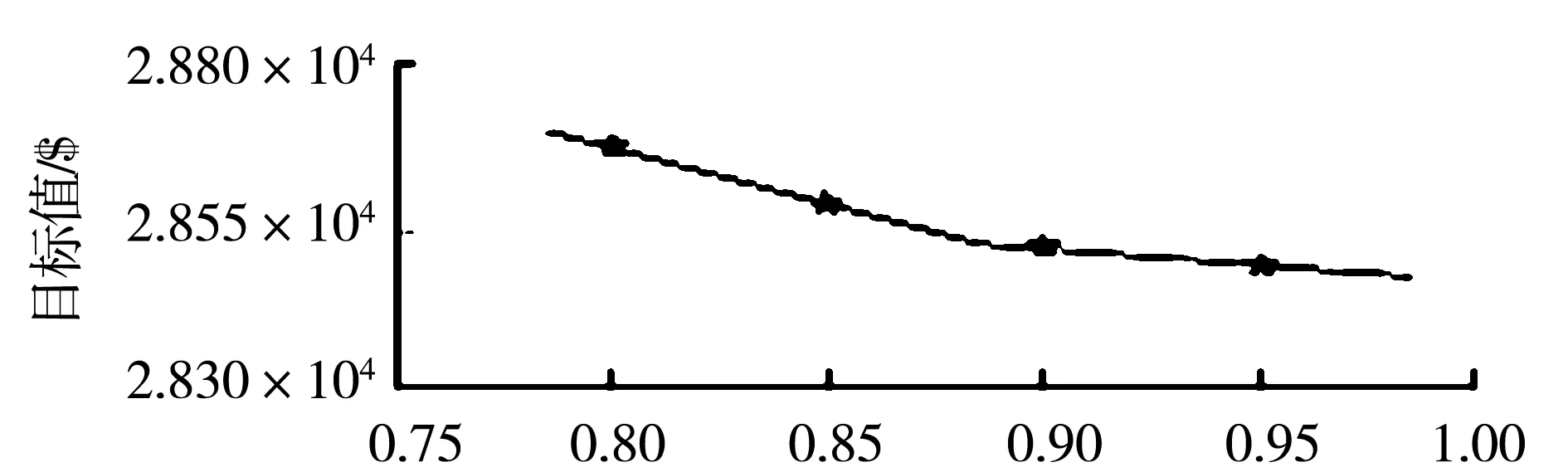
图3 不同置信水平下的目标值变化图

从分析中可以看出，置信水平越高，目标函数值越小。

6 结束语

文中主要探究风电混合储能容量配置方法以及策略，结合某风电场进行验证。采用DFT处理不平衡功率，且确定多介质储能容量。同时提出频率确定方法，利用多介质储能补偿，实现最优处理。在确定储能容量的基础上，建立以利润最大为目标的机会约束规划储能运行策略模型，最后通过实际算例，发现目标与目标值结果最为靠近，且置信水平越高，函数值越小。希望通过文中的分析，可以为风电场多介质储能系统容量的配置提供可行性建议。