1-D和2-D导热模型对LOCA事故的影响

，， ，

(中国原子能科学研究院，北京 102413)

0 引 言

再淹没阶段是缓解LOCA事故进程的最关键阶段，在这个阶段中冷却剂从下腔室逐渐上升并为元件提供冷却，在冷却剂上升过程中，浸润点前后的元件轴向段会存在较大的温度梯度从而引起一定的轴向传热[1]。利用1-D和2-D导热模型，即是否考虑元件的轴向导热，会对LOCA事故中再淹没阶段元件包壳的峰值温度计算结果产生一定的影响，并且2-D导热模型对于严重事故的计算分析有重要意义，在LOCA事故向严重事故拓展的过程中，初始温度场会对严重事故的评价产生一定影响，因此有必要对应用两种导热模型的LOCA事故进行对比计算。文中选用RELAP程序和SCDAP程序为分析工具，建立了两种计算输入，分别依托RELAP程序中Heat Structure的1-D导热模型和SCDAP程序中Fuel Component的2-D导热模型，在调稳完成后计算了三种喷放系数的LOCA事故，以分析这两种导热模型在计算LOCA事故进程中所造成的差别[2]。

SCDAP/RELAP程序是目前应用较为广泛的反应堆事故分析程序。RELAP程序能够较好的对压水堆核电厂各种瞬态工况进行模拟，其用于模拟堆芯部分的Heat Structure在计算传热时采用的是一维有限差分导热方程[3]。SCDAP程序含有多种严重事故分析模块，通过耦合RELAP程序的水力学计算部分可以将功能拓展至严重事故的计算范畴。SCDAP程序中的导热计算采用的是二维有限差分导热方程，可以在事故进程中同时计算沿轴向和径向的导热从而得到温度分布的计算结果[4]。用于文中计算的两种输入卡仅在堆芯建模部分有区别，从而最大限度的排除核电厂其余部分对计算结果的干扰。

1 导热模型简析

RELAP程序中用于数值计算的1-D导热方程的积分形式如下公式(1)所示：

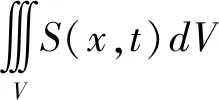
(1)

通过给定其边界条件即可以得到此一维导热方程的数值解和沿径向的温度场。SCDAP程序中采用的二维有限差分导热方程形式较为特殊，求解方法采用交替格式隐式，文中介绍其一种简化形式，用下图和公式(2)来说明：

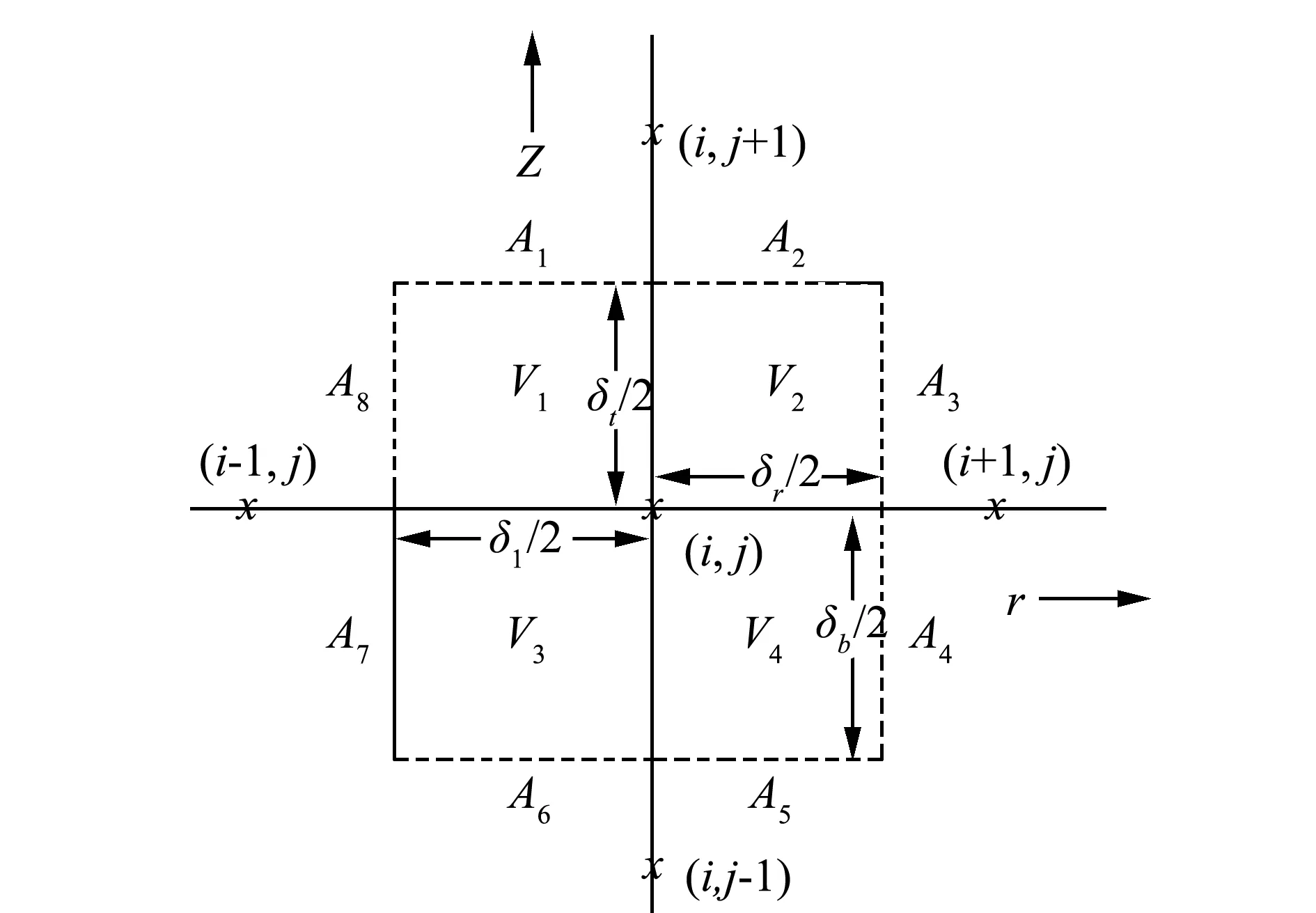
图1 节点i， j的计算域

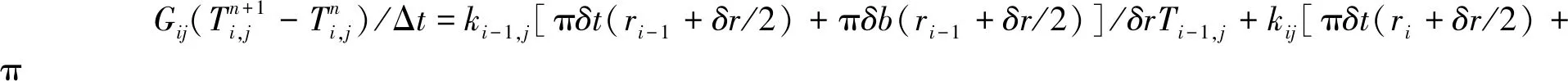
(2)

上述的两种导热方程都是基于能量守恒定律和傅里叶导热定律推导而来，二维导热方程可以同时在计算域内求解沿X，Y两个方向的热传导，即可以在事故过程中同时计算元件沿轴向和径向的热传导。

2 计算过程简述

文中所采用的计算分析方法主要分为以下三个阶段：

(1)首先建立适用于RELAP程序和SCDAP程序运行至稳态的计算输入，并且将两种堆芯模型的关键计算参数与电厂运行的真实参数相比较，以确保两种堆芯建模方案的正确性和一致性。

(2)在位于一个环路的安注点和堆芯入口处的冷管段处建立破口模型，分别采用三种不同的喷放系数来反映三种不同破口尺寸条件下的失水事故进程。

(3)将两种堆芯模型下的关键参数进行比较，对比两种导热模型对LOCA事故关键参数的影响。

3 稳态建模过程及调稳参数比较

M310堆型是一种三环路的百万千瓦级压水堆核电厂，这个厂的热功率为2 895 MWt，运行压力为15.5 MPa。文中用于RELAP程序和SCDAP程序计算的全场节点化示意图如图2所示。

图2 用于RELAP程序计算的全场节点化示意图

此模型包含一回路的所有关键部件，能够较好的反映在LOCA事故计算过程中一回路与堆芯的主要参数变化情况，在堆芯模型部分采用的是简化建模方案，即用一个平均棒来代表堆内的燃料部分，同时考虑到SCDAP程序轴向分段的上限以及方便比较计算结果，RELAP和SDDAP的堆芯模型在轴向上都划分了10个计算节点。

在RELAP程序的堆芯建模方案中，用一个Heat Structure构件代表平均棒，用一个水力学控制体Volume来代表通过堆芯的冷却剂通道。在SCDAP程序中用一个Fuel Rod Component来代表平均棒，同样用一个水力学控制体Volume来代表通过堆芯的冷却剂通道，二者在建立堆芯模型时所采用的尺寸及物性参数完全一致。下图为两种输入稳态计算的关键参数比较。

图3 两种输入稳态计算的系统压力

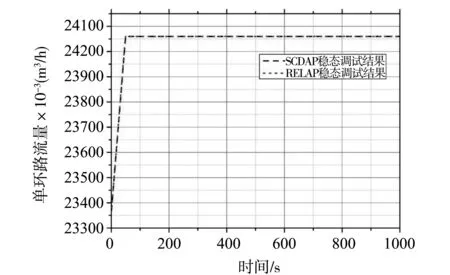
图4 两种输入稳态计算的环路流量

图5 两种输入稳态计算的堆芯平均温度

两种输入与M310电厂的稳态运行参数对比：

表1 M310堆型参数设计值与两种输入稳态运行参数比较

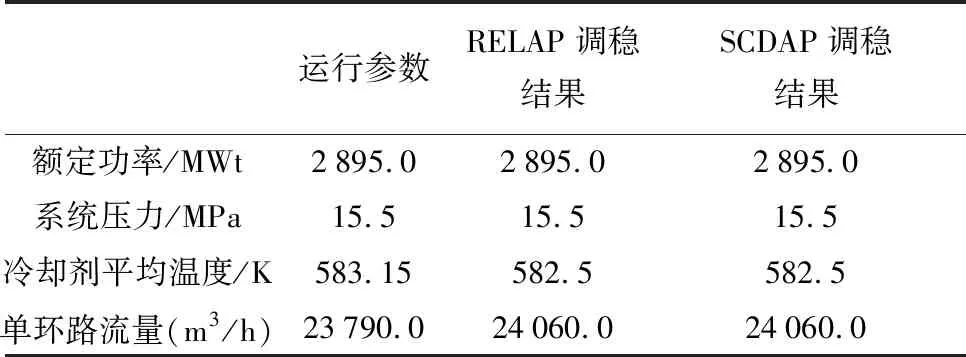
运行参数RELAP调稳结果SCDAP调稳结果额定功率/MWt2895.02895.02895.0系统压力/MPa15.515.515.5冷却剂平均温度/K583.15582.5582.5单环路流量(m3/h)23790.024060.024060.0

两种程序的稳态计算结果与核电厂稳态运行参数对比的差值均小于5%，因此可以认为这两种模型可以较好的反应核电厂稳态运行时的真实状态。

图6 两种输入稳态计算的三个轴向段温度

4 破口模型及瞬态计算方法

文中为了更充分的对比两种堆芯模型下的LOCA事故关键参数变化进程，在建立模型时采用了SCDAP/RELAP程序说明书中推荐的两种建模方案[5]。

第一种破口建模方案是通过在假想的发生断裂的管段上加上一个与时间相关的闸，并通过一个单接管(950)将从破口处喷出的流体引入安全壳(960)。通过定义不同的两相喷放系数可以实现多种破口尺寸的LOCA计算。破口模型如图7所示。

图7 计算采用的第一种建模方案

第二种建模方案主要用于计算双端剪切断裂的情况，即事故开始后冷却剂完全从破口处喷向安全壳内。双端剪切断裂的破口模型如图8所示。

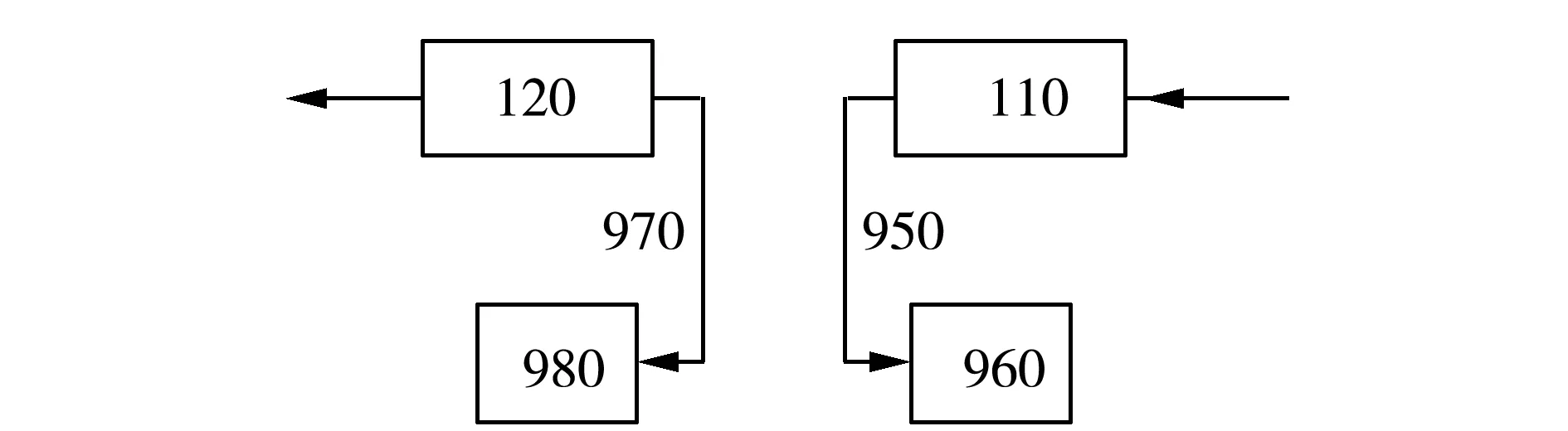
图8 双端剪切断裂的破口模型

对于两种建模方案而言，其具体的计算过程都是首先让输入卡运行至稳态，再在再启动(restart)卡上加上相应的破口模型，进入瞬态过程的计算，瞬态计算所采用的停堆逻辑和事故缓解控制完全相同。

5 主要计算结果展示

文中主要计算了两种堆芯模型三种破口尺寸条件下的LOCA事故进程，首先展示对冷管段双端剪切断裂工况的计算结果。以下两张图是事故计算开始后堆功率和系统压力的对比计算结果，同时为了方便比较事故开始前后的参数变化情况，本章节的计算结果中前200S的参数为稳态计算值。

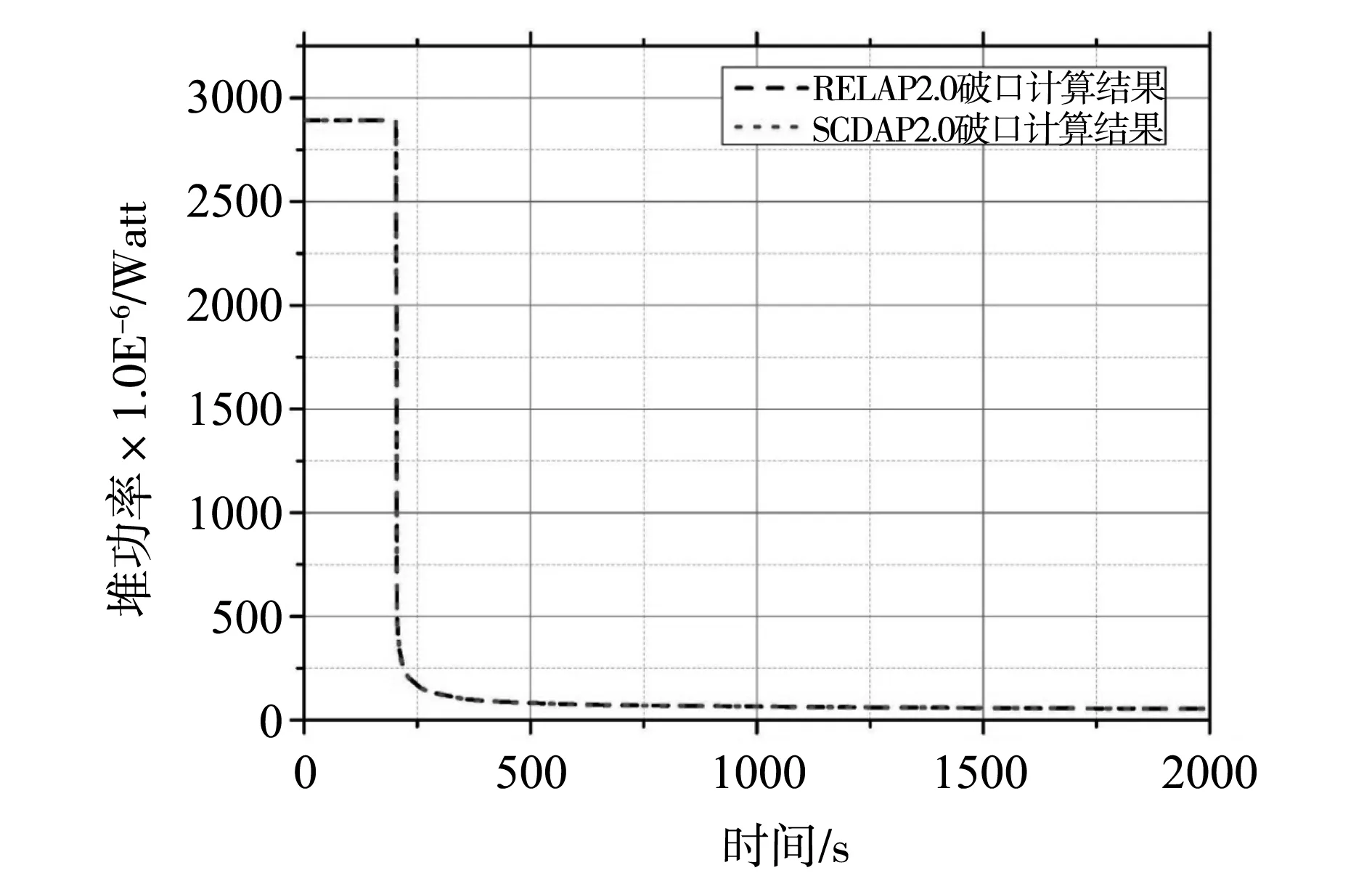
图9 堆功率对比计算结果

从上述两张图中我们可以得知，在发生双端剪切断裂后，由于冷却剂从破口处大量的喷出，系统压力快速下降到稳压器压力低-低的停堆信号，快速停堆后堆功率迅速衰减为衰变热状态。

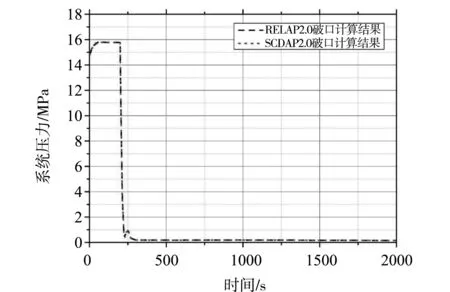
图10 系统压力对比计算结果

我们可以从两张图中看到，两种堆芯模型在瞬态过程中计算得到的功率变化和压力变化情况等系统参数吻合的很好，基本可以排除除导热模型外的其他参数对计算结果的影响，从而更好的反映两种导热模型对燃料元件在LOCA事故过程中温度变化的影响。

在冷管段双端剪切断裂的计算中，主要展示燃料元件包壳轴向第8、9、10段的温度变化情况和堆芯水位的变化情况，来说明这两种导热模型在事故中对温度变化的影响，这三个轴向段是建模过程中元件的后三个轴向段，也是整个LOCA事故进程中工况较为恶化的三段。其在瞬态过程中的温度变化对比结果如图11-12所示。

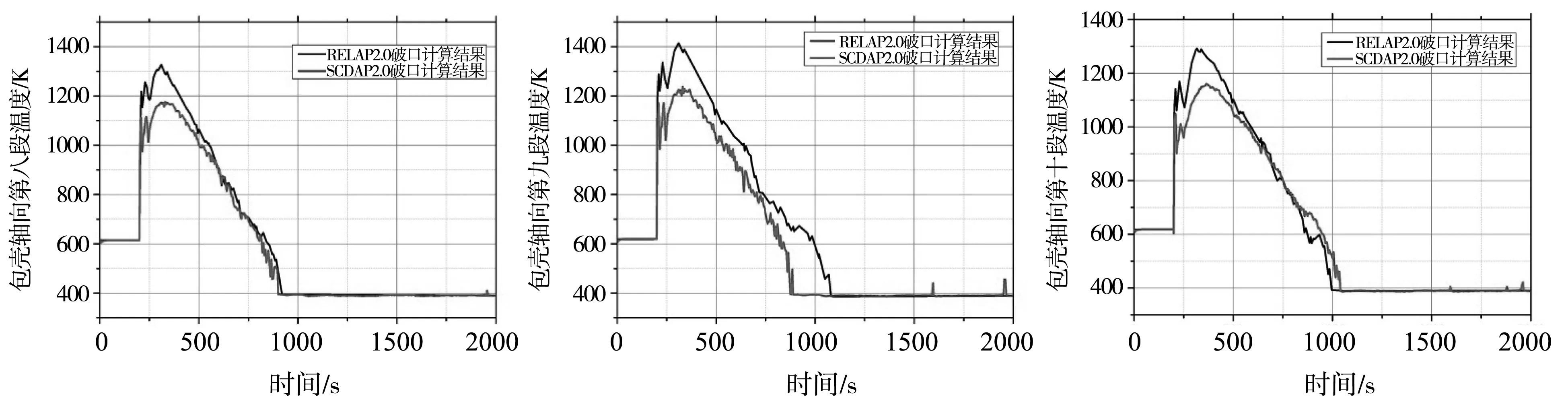
图11 双端剪切断裂包壳轴向段温度对比计算结果

图12 堆芯水位对比计算结果

喷放系数取1.7和1.4时，主要展示两种堆芯模型包壳轴向段的后三段温度变化情况，如图13-14所示。

7 结束语

通过对以上三种计算结果的分析，可以得到如下结论：

(1)两种模型在计算M310电厂稳态运行和LOCA事故中的系统参数对比时，具有较好的一致性，这确保了文中所建立的两种计算模型的正确性和一致性。

(2)在事故计算过程中，2-D导热模型对元件包壳峰值温度的预测会显著低于1-D导热模型的预测值。在破口事故发生的瞬间，由于流过堆芯的冷却剂大量从破口处喷放导致燃料元件的冷却条件迅速恶化从而产生一个很大的温度跃升。1-D导热模型所预测的轴向段高功率点的温度跃升值会显著高于2-D导热模型的预测值。在2-D导热模型的计算结果中，由于轴向导热的存在，高功率点会向上下两个轴向段传热从而降低其温度跃升值并使元件的轴向温度梯度小于1-D导热模型的预测值。

图13 喷放系数取1.7时包壳轴向段温度对比计算结果

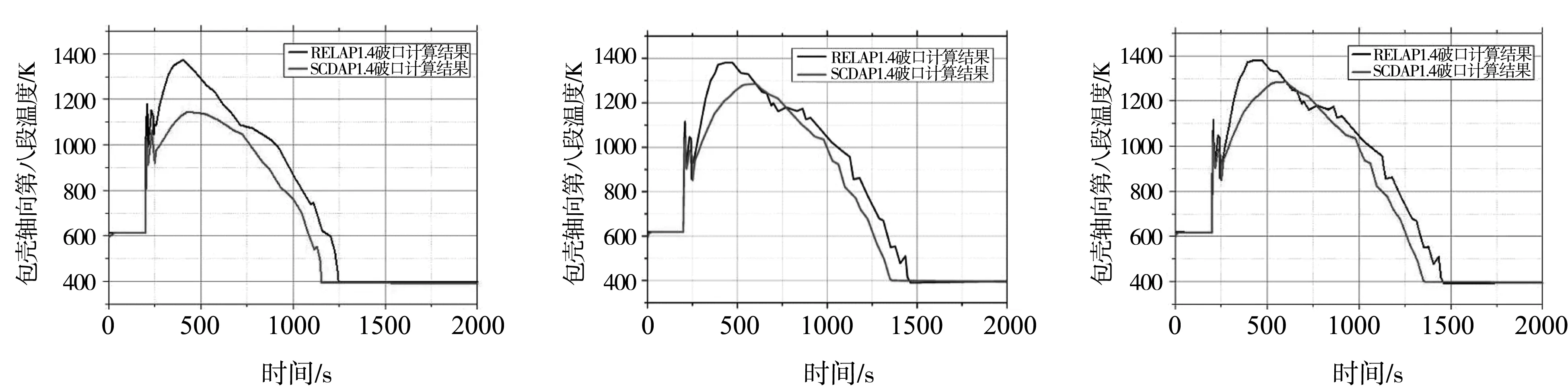
图14 喷放系数取1.4时包壳轴向段温度对比计算结果

(3)在再淹没时间的计算上，1-D导热模型和2-D导热模型的预测值同样显示出一定的差异性。2-D导热模型的预测值会稍快于1-D导热模型的预测值，因为轴向导热的存在，未被浸润的轴向段会向浸润后的轴向段传热从而加快自身的冷却速度。相较于对元件包壳峰值温度的预测情况，两种导热模型对再淹没时间预测的差异性较小。