装配式钢桁架桥桥跨结构故障诊断

陈华明，徐 磊，何晓晖

(陆军工程大学野战工程学院， 南京 210007)

在无损状态下，对物体进行检测方法有电测法、超声波检测法、化学检测法和模态分析法等。对于不同的物体的具有的特征不同和周围环境的区别，使用条件的限制使得每种检测方法都有一定的条件。目前还没有能够适应任何物体和任何环境的检测方法[1-3]。在工程实际运用时，往往工程预算成为限制检测方法的主要因素，常由于运算不足导致检测方法受限，最终产生检测结果不理想等问题。在诸多的检测方法中，模态分析法在应用到大型工程机械结构上具有独到的优势，一方面其本身不需要投入很大的资金就可以有较为精确的检测结果，同时对于操作人员来说，操作简便，直观性较强，使其在工程装备的故障检测中应用很广，也是国内外整体结构检测技术研究的热点[4-8]。

本文首先依据模态分析的理论对桥梁结构的振型进行了理论分析，在此基础上，在ANSYS仿真平台中建立了桥跨结构的模型，并进行了参数设置，之后分别在无损伤和有损伤条件下进行了仿真，通过对仿真结果进行分析可以得到桥跨结构损伤现象和易损伤位置，最后通过实装试验来对仿真分析结果进行验证，最终完成对桥跨结构故障的诊断。

1 理论分析

桥梁桥跨结构的特征值方程如式(1)所示。

(K-λiM)φi=0，i=1,2,…

(1)

式中：K、M分别表示桥梁结构的整体刚度矩阵和质量矩阵；λi是特征值；φi是对应的位移模态。

对于钢桁架桥梁结构，其损伤往往导致结构刚度明显降低，对质量分布几乎不产生影响，相应地使λi和φi产生改变。

损伤结构运动方程的摄动方程表示为式(2)。

[(K+Ki)-(λi+Δλi)M)]ψi=0,i=1,2,…

(2)

式中：ΔK、Δλi分别表示整体刚度矩阵和特征值的改变量；ψi是结构损伤后对应的位移模态。

从以上两式可看出，结构的特征频率和振动模态的变化反映出结构刚度的分布和变化。对结构损伤前后的振动模态进行规一化处理，φi、ψi分别满足式(3)和式(4)：

(3)

(4)

进一步计算可得结构振动模态变化列向量为

Δi=φi-ψi

(5)

通过计算，最终得到模态变化向量的最大值表达式为

δj=max|Δi|

(6)

分析δj的特性可以得到物体结构损伤的位置，其值的大小代表结构损伤的程度[9-10]。

2 桥跨结构的模型建立与仿真

为了验证上述损伤判据应用于某冲击桥桥跨结构故障诊断的可行性，首先利用有限元法对桥跨结构进行动力特性分析，根据分析结构对对桥跨结构进行损伤模拟，主要观察桥跨结构的振型[12-13]。

2.1 模型建立

如图1所示，某型装配式钢桁架桥桥节主体材料为铝合金，采用车辙式结构，一个桥节由两个车辙组成。两个车辙之间由横向连接系和拉杆相连。桥跨长18m，宽3.2m，跨中高0.659m(包括防滑块)，主要由顶块、单耳、双耳、横向连接系、车撤、拉杆、桥面和梁等部件构成，为了模型的简化现主要对桥梁的桥跨结构进行建模。

1.顶块；2.单耳； 3.双耳； 4.横向连接系； 5.车辙； 6.拉杆

采用ANSYS建立桥跨结构的有限元模型。结合桥梁的结构特点，桥梁是双车辙箱梁式结构，为了尽可能模拟桥梁的关键结构，在大量试算分析的基础上，确定采用梁单元BEAM189模拟T型肋板、连接横梁等梁式结构13-14]。所建立的有限元模型如图2。

通过壳单元SHELL63来模拟桥梁的桥面板、腹板等板式结构，并耦合关键节点的自由度。所建立的桥面板和腹板有限元模型如图3。

图3 板结构有限元模型

设定桥梁动力特性分析的约束条件为简支，一端约束全部自由度，另一端仅约束竖向和纵向自由度。考虑到计算结果的准确性，在参数设定均采用装备的实装尺寸，防止产生缩尺效应[15]，最终建立的ANSYS模型如图4。

图4 动力特性分析的有限元模型

下面主要对桥跨结构的在无损伤和有损伤两种情况下进行模态分析。

2.2 模型仿真

1) 桥跨结构在无损伤状态下

图5给出了桥跨无损伤条件下的1～10阶模态振型(由于篇幅限制只给出了第1和第10两阶振型)。

图5 桥跨结构无损伤条件下的振型

2) 桥跨结构有损状态下

图6给出了桥跨有损伤条件下的1～10阶模态振型(由于篇幅限制只给出了第1、第2、第9和第10共四阶振型)。

图6 桥跨结构有损条件下的振型

表1给出了桥跨结构在有损和无损条件下各阶固有频率，表2给出了桥跨在有损和无损条件下一阶竖弯在不同测点的振幅。

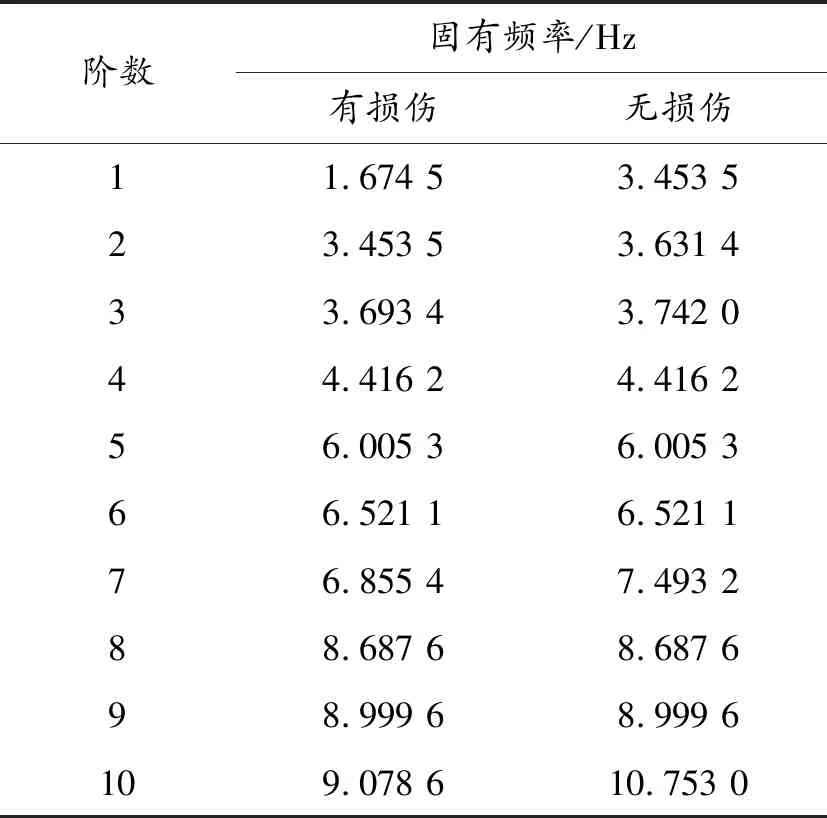
表1 桥跨结构有损和无损条件下固有频率

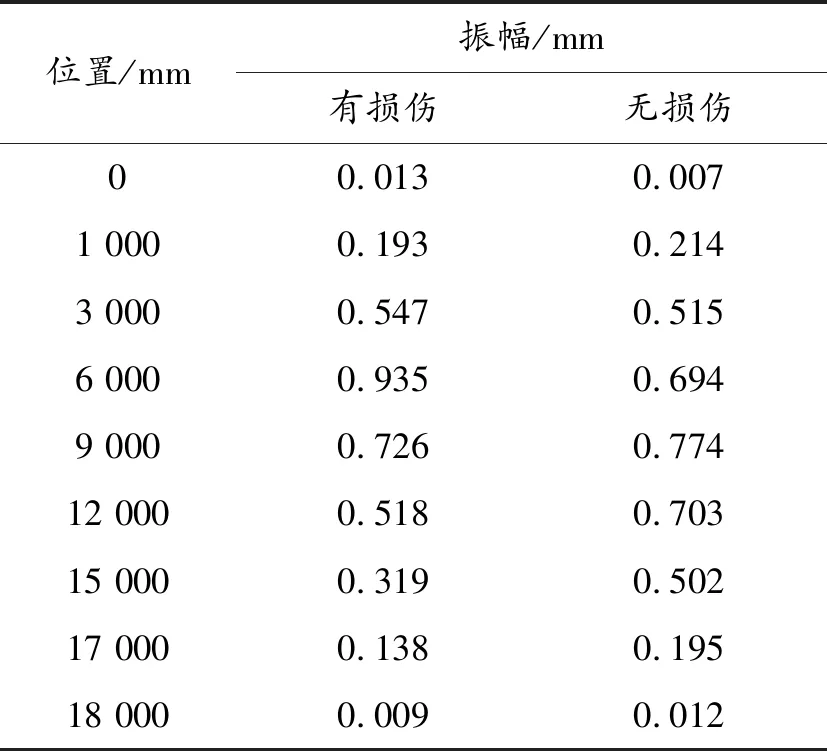
表2 桥跨结构在有损和无损条件下一阶竖弯在不同测点的振幅

3 桥跨结构损伤识别

对桥跨的结构损伤识别主要包括损伤现象的识别和损伤位置的识别。

3.1 损伤现象的识别

图7给出了桥跨无损伤和有损伤条件下的各阶固有频率的变化。

从图7可以明显看出，当桥跨在无损伤和有损伤下的条件下时，桥跨的各阶固有频率均有不同程度的下降，同时，对桥跨而言，其低阶和高阶固有频率对结构损伤的反映更为明显，因此，可选择低阶或高阶固有频率作为结构损伤参数来判定结构是否损伤与损伤程度。

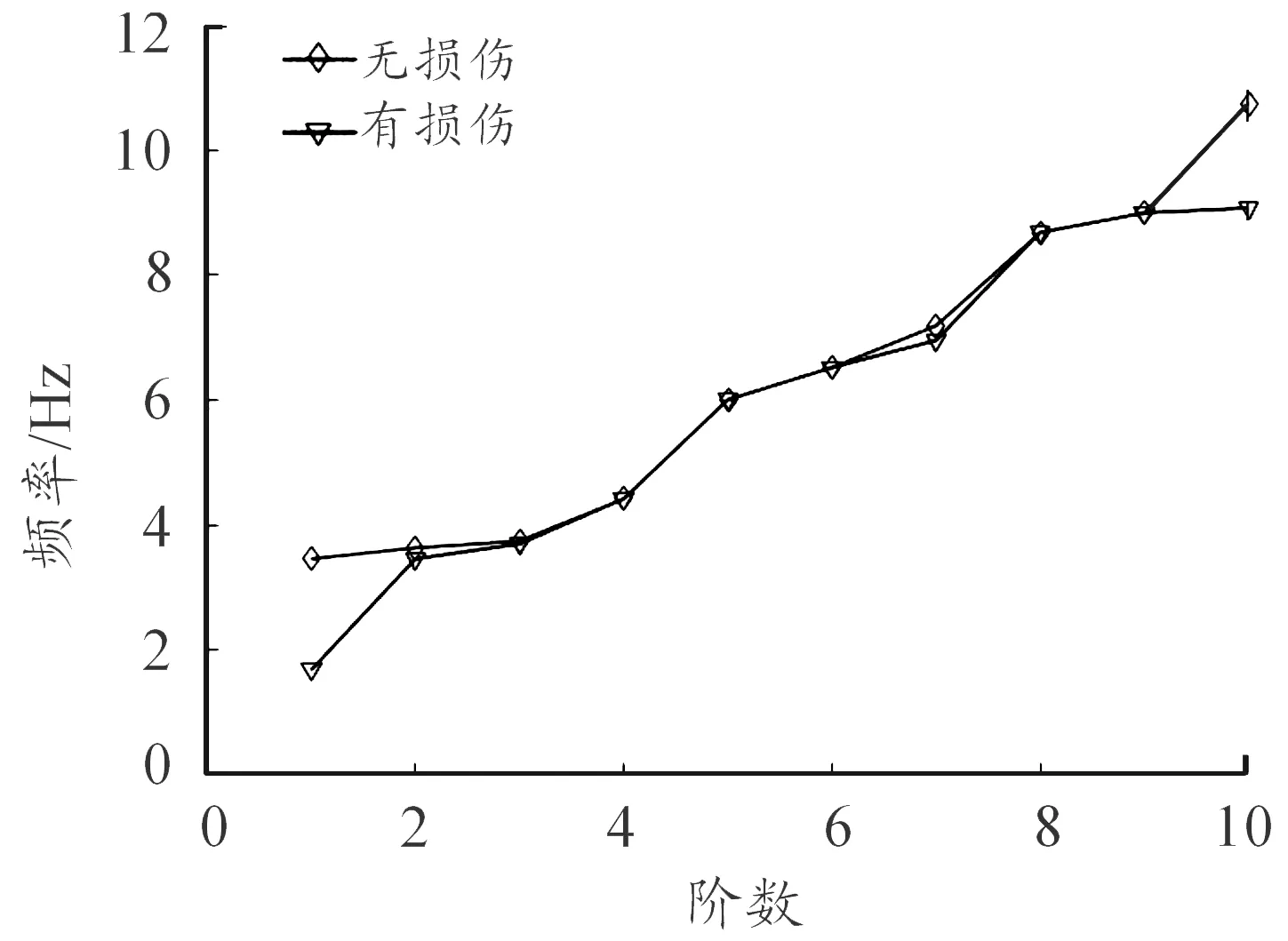
图7 桥跨无损伤和有损伤条件下的固有频率

3.2 损伤位置的识别

采用低阶或高阶固有频率作为结构损伤参数能够判断结构是否损伤及损伤的程度，但并不能判断结构损伤的位置。对此问题，本文在总结前人成果的基础上，采用图谱分析的方法解决，通过分析结构的振型图或振幅曲线确定损伤位置。其中，振型图分析法是通过比较损伤结构与无损伤结构的振型图直接确定，其依据是出现损伤的结构其振型图与无损伤结构相比，在损伤位置会出现较为明显的变化，出现变化的区域也就是损伤的位置。图8为桥跨在无损伤和有损伤条件下的振型。

图8 桥跨不同程度损伤条件下的振型

从图8可以看出，桥跨有损伤的B区域与无损伤的A区域存在明显的区别，B区域明显“凸起”，该区域即为损伤位置。

当振型图分析方法难以确定时，可采用振幅图分析法。该方法是进一步得出结构在某阶振型下的振幅图，通过振幅分析确定。图9为桥跨有损和无损条件下一阶竖弯的振幅曲线。

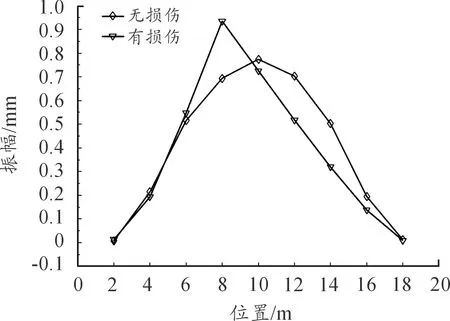
图9 桥跨无损伤和有损伤条件下一阶竖弯的振幅曲线

从图9可以看出，在桥跨无损伤时一阶竖弯的振幅曲线是一条较为光滑的曲线，而一旦结构出现损伤，振幅曲线将变得不光滑，而出现“突变”的区域也就是结构损伤的位置，而“突变”程度也反映了结构损伤的程度。

4 实装试验

为了验证仿真分析的结果的，本文结合理论和仿真分析结果，对某冲击桥进行动力特性实装试验。

采用基于环境激励的谱分析方法开展实装试验研究。试验现场只有7个模块，由于试验仪器数量的限制，采用了分段试验的方法。根据桥跨结构特点及现场的试验条件，在每个桥面上共均匀布置7个测点，每个桥面上均有一个参考点，每个测点放置一个加速度传感器，不知传感器时需要保证严格的垂直度和水平度，如图10所示。

图10 动力特性实装试验

图11～图14给出了桥跨结构在无损伤条件下不同方向的振型试验结果与仿真结果。

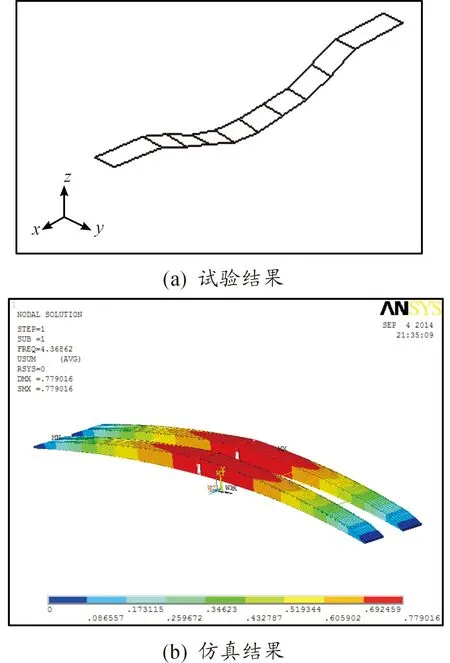
图11 无损伤一阶竖弯

图12 无损伤二阶竖弯

图13 无损伤一阶侧弯

表3给出了桥跨结构的模态试验与仿真结果。从表3可以得出：经过试验采集的数据进行有限元计算后，得到的振型与ANSYS仿真的得到的振型大致相同，验证了仿真分析结果的可信性。通过对比发现二者固有频率相差很小，最大误差为5.73%，最小误差为2.48%。经过分析产生偏差的原因可能是建立模型时，初始条件和装备参数的设置与实际参数存在一定的差异和装备本身存在一定的结构缺陷。

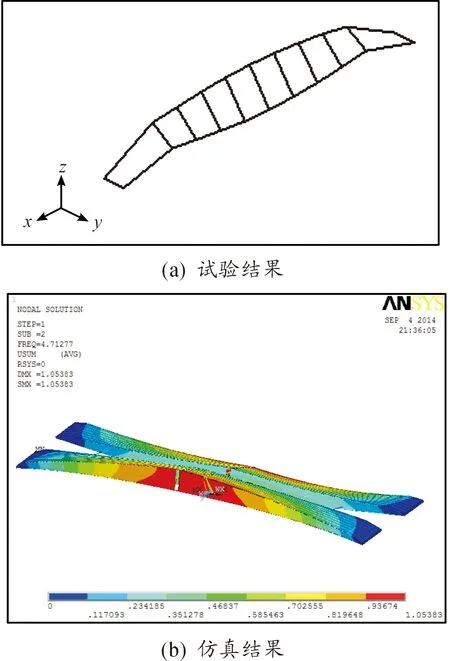
图14 无损伤一阶扭转

表3 桥跨结构的仿真和试验结果

5 结论

1) 通过比对无损伤与有损伤结构的固有频率曲线，判定结构是否存在损伤及损伤的程度。其准则是比对现有结构与无损伤结构的低阶或高阶固有频率，如出现明显变化表明现有结构存在损伤，而变化的程度则表征损伤的程度；

2) 通过比对无损伤与有损伤结构的振型图或振幅曲线，判定结构损伤位置及损伤程度。其准则是比对现有结构与无损伤结构的振型图或振幅曲线，如图形或曲线发生“突变”，表明现有结构存在损伤，“突变”的区域即损伤的位置，而“突变”的程度也表征损伤的程度。

3) 验证了仿真研究结果的可信性，可以对桥跨结构在不同的损伤条件下仿真，对桥跨结构进行故障诊断。