在不断“叩问”中完善教学设计——以“合并同类项（1）”教学为例

■姜鸿雁

（作者单位：江苏省无锡市河埒中学）

结合多年的教学经历，笔者认为，课堂教学活动的设计与展开，是教师在备课过程中不断叩问自己的物化呈现。那么，教师到底要叩问自己什么呢？笔者在此次活动中开设题为“合并同类项（1）”（苏科版教材七年级上册第三章第4节第一课时）观摩课，回想本节课的设计与展示的过程，联系日常教学，深深感觉到，教师需要不断叩问自己：学生为什么要学习这节内容，即教学目标的定位、价值取向在哪里？怎么学习这节内容，即通过怎样的教学过程能够较好地实现教学目标与教学价值？如果以后再上这节内容，应作怎样的改进？即教学反思。以本节课为例，笔者谈谈一些想法，期待大家批评指正。

一、教学设计的主要流程及意图

1.创设适当问题情境，激活知识生长点，感受数学抽象。

问题1 算一算，看谁算得快。

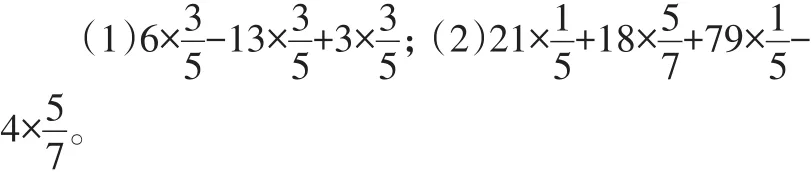
设计意图：从前一章熟悉的有理数运算开始，唤醒学生对“算理”的认识，也是为下面用字母表示数的学习做准备，“数的运算”是“式的运算”的生长点，本节课的起点在此。

问题2 变一变，看谁还会算。

（1）6a-13a+3a；（2）21a+18b+79a-4b。

设计意图：这里用字母代替数，对于学生来说是最近发展区，在运算之余，让学生回味运算结果与原式相比具有简约之美。自然地体现用字母表示数具有一般性，体现数学抽象；对比中感受“数式相通”；在生活中“同一类物体可以合并”，在数学中“同一类式子也可以合并”，而且在“合并”中享受简约，从而产生识别“同一类式子很重要”的学习欲望，使“建构同类项的概念”呼之欲出，给学生进一步学习新知营造“愤悱”的心理状态。

2.营造开放思维场所，建构同类项概念，提炼合并法则。

问题3 分一分，看谁分得合理。

a，-3，5mn，-7a2b，10nm，5.1，6a，-8a2c，-7ab2，2ba2。

设计意图：学生在学习有理数时，已有经验——随着认识的“数”增多，分类可以化“无序”为“有序”，且为运算带来方便。经类比，“式”也是如此。前面已有对代数式（主要是整式）分类的学习经历，单项式是代数式的“细胞”，对单项式“分类”是为运算服务的，是建构“同类项概念”的重要环节。同时，本环节没有给出明确的分类标准，旨在为学生的思维营造开放的空间，学生自定标准，则会有不同标准，必然产生不同的分类结果，对不同的分类结果作对比，最终以“能合并”为“最科学”的标准，确定分类结果。接着，对分类的结果观察、归纳、总结，学会用数学的语言表达，在不知不觉中完成“同类项概念”的自我建构；同时在合并的过程中，在乘法分配律的基础上，提炼合并同类项法则。

3.通过各种变式练习，辨析同类项概念，初步运用法则。

问题4 填一填，使各组单项式构成同类项。

（1）3a□b3与-10b□a4；（2）2xy□z3与-x□z3y2；（3）mn3与□n□m□。

问题5 试一试。

已知单项式2a3bn+1与-8am-2b2能够合并成一项，则2m+3n的值是______；它们合并出的结果是______。

问题6 辨一辨，下列运算结果是否正确。

（1）2x+5y=7xy（ ）；（2）6ab-ab=5（ ）；（3）8x3y-9x3y=x3y（ ）；（4）-m2n+nm2=0（ ）；（5）p3q2-5m-7p3q2=-6p3q2-5m（ ）。

问题7 填一填，使下列等式成立。

（1）2xy+（ ）=7xy；（2）-a2b-（ ）=a2b；

（3）m2+m+（ ）+（ ）-1=3m2-2m-1。

设计意图：通过变式练习，巩固同类项概念、合并同类项法则。

4.借助例题，规范展示，巩固法则运用，落实数学运算。

问题8 合并同类项：

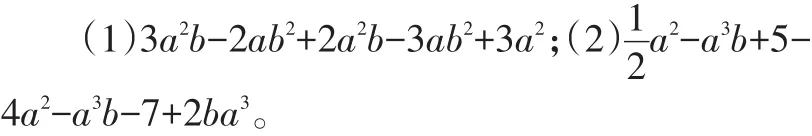
设计意图：通过例题，规范书写格式，让学生经历先“找”同类项（在解决问题的过程中进一步巩固同类项概念），再“搬”同类项（在解决问题的过程中感受加法交换律），最后“合”同类项（在解决问题的过程中进一步巩固合并同类项法则）的过程，使数学运算这一素养落地生根，并在“合”的过程中，体会“式的运算”最终是转化为“数的运算”，再次体会“数式相通”，让学生再次感受“式”是在“数”的基础上生长并发展起来的。逐步让学生感到数学的学习是前后一致，逻辑连贯，一以贯之的。

5.深入应用法则，体现整体思想，埋下新的生长点。

问题9 合并同类项：

（1）3（a+b）2-2（a+b）+（a+b）2-3（a+b）；（2）3 2+4 5-2 2+3 5。

设计意图：无论是合并整体思想下的“同类项”，还是合并同类二次根式，都与合并同类项同宗同源、一脉相承，在学生能接受的情况下，加以渗透，体现整体教学理念。

二、影响教学设计的几点思考

1.确定科学的教学目标是课堂教学的“魂魄”。

教师在备课时，需要不断叩问自己：为什么要学习这部分内容？本节内容的教学价值在哪里？这是一节课的“灵魂”所在，也决定这一节课的高度与深度，对教学过程的设计与实施起着统领的作用。笔者结合自己的一些经验，认为可以从以下几个切入点对一节课的教学目标进行定位。

（1）这节课要实现的最基本的知识技能目标是什么？

一节课的基本知识、基本技能是渗透数学思想方法、落实素养的载体，是看得见、摸得着的内容，对于学生来说是最能感知得到的新知识，也是一节课的最基本目标。作为一名教师，准确地对这部分内容定位，是最基本的要求。“合并同类项（1）”这节课，让学生明白什么是同类项，会合并同类项是本节课的基本知识技能目标。如何在教学过程中实现它们，在实现它们的过程中还要带给学生什么？这是教师必须思考的。

（2）这节课在整个知识链体系中的地位、价值是什么？

一个具体的知识点、基本的技能不是孤立存在着的，它在整个知识框架、知识体系中的地位、价值是什么？它从哪里来？将到哪里去？教师弄清这些，有助于提升课堂的立意，更精准地把握课堂教学的节奏。本节课的“前生”来自有理数的加减运算、乘法分配律、单项式的相关概念，是学生真正接触“式运算”的开篇起始，是将来对方程、不等式、函数关系式准确进行化简变形的“童子功”，是二次根式加减运算的前奏，是渗透“数式相通”、体现转化思想的很好资源。有了以上认识后，所有的教学活动都将为体现这些地位、实现价值而努力。

（3）这节课能让哪些核心素养落地生根？

自从《普通高中数学课程标准（2017年版）》正式颁发以来，发展学生核心素养已经成为数学课程的核心目标，必然对初中的数学教学起着不可估量的导向作用。作为课程目标，实现它不可能一节课就能做到，但一定是由每节课点点滴滴“汇聚”而成的，对于每节课的教学设计，都该“不忘初心”，才能使课堂教学“牢记使命”，不迷失方向。本节课，在体现“数式相通”的过程中，通过字母表示数体现数学抽象，让学生感受“式”比“数”更具有一般性；在对单项式分类时，学生在自我建构同类项概念的过程中，学会用数学的语言表达，这是数学建模的萌芽；在合并同类项的过程中，让学生明白算理，这是推理与数学运算并行。如此设计教学过程，能让相关核心素养落地生根。可以说，基本知识技能是载体，基本思想方法是途径，核心素养是终极目标。

2.设计“配套”的教学过程是课堂教学的“血肉”。

没有切实可行的“配套”的教学过程作支撑，再科学的目标定位也只是方向，只是浮云，所以教师需要不断叩问自己：学生经历怎样的学习过程，才能实现一个个既定目标？笔者结合自己的教学实践和本节课的教学体会，认为可以从以下几个着手点来设计教学过程。

（1）这节课的学习起点在哪里？

学生的学习是在一定的情境下展开的，是一节课起航的地方。情境可以是数学情境，也可以是生活情境。对于本节课，有的教师是从生活情境开始的，生活中对物品等进行分类是常有的事，以此迁移到数学，也可以对“式”进行分类，从而开始了同类项概念的学习，笔者也曾如此设计过。而这次教学设计，改变了以往的方式，把起点定格在数学内部的情境：有理数的运算。在“数式相通”中展开“式的合并”，在“合并”中感受简约，在简约中认识到“识别一伙儿”很重要，于是产生对同类项概念学习的心理需求，笔者认为这不仅能更好地体现数学味，更能让学生体会到弄清同类项概念是学习的需要，而不是老师强加给他们的，“以人为本”的教学观在这些看似细微的教学设计中反映了出来。

（2）如何“呵护”并促进起点“茁壮成长”？

一个新知识、新技能形成之后，需要适当的巩固，形成较为稳定的认知。改变问题的呈现方式，设计各种变式练习是一种较为常见的教学手段。笔者通过一系列的辨析题型，让刚刚建构的概念稳固一些，刚刚形成的技能熟练一些。在这个环节中，教学手段、方式的多样化，可以增加学生的学习兴趣，从而提高课堂效率。

3.进行深刻的教学反思是教育教学的希望。

设计本节课时，笔者联想到几年前上的这节课的情景，并将当时的教学设计、PPT进行“反刍”。相比之下，有如下两点明显变化：一是前面提到的教学情境的设计变化，同类项概念与合并同类项的先后顺序完全相反。笔者认为，本次设计是符合人的认知规律的体现，在合并“同类”中感受简约，在感受简约的过程中，产生把“同类”的特征找出来并下定义的心理需求。相比之下，以前的教学设计是笔者对“为什么学习本节课”的认识不太深刻的结果。二是同类项概念的形成更着重于学生自我建构。本设计是在学生有了初步的合并同类项的经历之后，教师创造平台，给学生自主空间，让学生在开放的思维场中自我建构同类项概念。学生数学地看世界、数学地表达世界的关键能力，在自我建构的过程中都得到了不同程度的发展。本节课上完之后，笔者感到环节3的问题设计有些碎片化，具体实施过程中形式也不够多样化；另外，从授课班级学生情况看，例题的设计起点高了一点，了解学情是课堂教学设计不可或缺的方面，这也导致环节5并没能在实际课堂教学中呈现出来，这些都是笔者以后再上本节内容值得思考、借鉴或改进的宝贵资源。课堂教学永远是遗憾的艺术，正是因为有遗憾，才让教师一直行走在追求完美的路上。对待教学，教师应怀着“虽不能至，心向往之”的情怀。

相信每位有教育情怀的教师上完一节课都有过这样的感受：如果课堂师生配合默契、思维碰撞、有意想不到的生成等现象，心情会非常愉悦；相反则心情会比较糟糕。心情愉悦也好，沮丧也罢，我们都应该思考，为什么会有较好的效果？要保留吗？发扬吗？为什么会产生不太好的结果？学生为何不能实现课前的预设？哪些需要摒弃？如何改进？总之，追问自己，以后再上这节内容，我该怎么上？所有这些思考，必然会影响这节课以后的教学设计。