把思维引向深入———《3的倍数特征》教学实录与设计意图

翟运胜（特级教师）

【教学内容】

苏教版五年级下册第33 页。

【教学目标】

1.使学生认识和掌握3 的倍数特征，能判断和写出3 的倍数，并能说明判断的理由。

2.使学生在经历探索和发现3 的倍数特征的过程中，培养观察、比较和分析等思维能力，积累数学活动经验，提高归纳推理的能力，进一步发展数感。

3.使学生主动参与探索、发现规律的活动，获得探索数学结论的成功感受。体会数学的奇妙，增强学习数学的积极情感，树立学习信心。

【教学过程】

一、提出猜想，引导质疑

师：判断一下，117 是不是2的倍数？是不是5 的倍数？

生：117 既不是2 倍数也不是5 的倍数。

师：117 为什么不是2 的倍数？为什么也不是5 的倍数呢？

生：个位上是0、2、4、6、8 的数是2 的倍数。个位上是0、5 的数是5 的倍数，117 的个位是7。

师：大家都是根据这个数字的个位判断的，谁来看着图说一说，判断一个数是不是2 或者5的倍数，只要看个位就可以了？

生：因为百位上100 一定是2 的倍数，十位上10 一定也是2的倍数，因此判断一个数是不是2 的倍数，只要看个位。

生：因为百位上100 一定是5 的倍数，十位上10 一定也是5的倍数，因此判断一个数是不是5 的倍数，只要看个位。

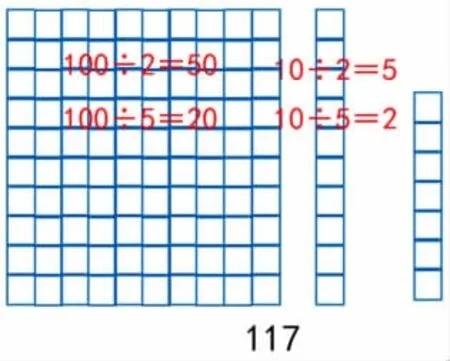
师：（出示下图）任何一个自然数，它的十位、百位、千位所代表的数都一定是2 或者5 的倍数，因此不需要再考虑了。影响一个数是不是2 或者5 的倍数，只是个位的原因，如果个位是2 或者5 的倍数，那么这个数就是2或者5 的倍数，否则不是。

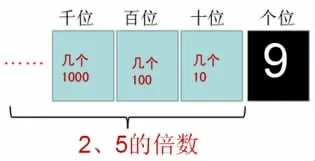
师：今天我们学习3 的倍数特征，判断一个数是不是3 的倍数，是不是也只要看个位呢？请大家猜一猜。

生：我猜也只要看个位就行。

师：请你猜一猜，如果只看个位，个位可能是哪些数就是3 的倍数呢？

生：个位上是3、6、9 的数。

生：不行，比如13 就不是3的倍数，26 也不是。如果一个数各个数位上的数字之和是3 的倍数，这个数就是3 的倍数。（这名学生在学习之前已从其他渠道知道了3 的倍数特征）

师：你知道为什么要把各个数位上的数字加在一起吗？到底个位上的数字能不能决定一个数是不是3 的倍数呢？（这名学生说不出理由）

【设计意图：通过先复习2、5的倍数特征，再利用数形结合的方式复习2、5 的倍数为什么只与这个数的个位有关，为之后研究3 的倍数特征提供思维路径的引导，有效促进深度学习。】

二、利用经验、组织探究

1.圈3 的倍数，发现3 的倍数的个位没有固定规律。

师：请同学们拿出百数表，圈出3 的倍数。

师：在百数表中，从排列上看，你有什么发现呢？

生：3 的倍数都在一条斜线上。

师：让我们来观察这些3 的倍数的个位。（引导学生观察比较：81、72、63、54、45、36、27、18、9）这一列，你有什么发现呢？

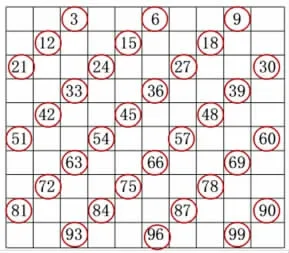
生：观察个位上的数，从0 到9 各种情况都有，没有固定规律。

师：看来3 的倍数，它的个位是没有明确的特征，只看个位是不行的。

【设计意图：学习之初，多数学生会猜测3 的倍数与这个数的个位有关，在运用百数表描画出3 的倍数以后，教师引导学生先观察81 这一斜行，学生会发现3的倍数的个位0～9 各种情况都有，从而确定了3 的倍数与个位没有明确的关系，诱发了认知冲突，促进学生进入愤悱状态，激起学生的探求欲望，促使学生产生积极的学习动机。】

2.从百数表中发现3 的倍数的规律。

师：从个位上看不出有什么规律，那么现在怎么办呢？观察这些3 的倍数（81 这一斜行上的数），让我们一起来读一读：9、18、27、36、45、54、63、72、81 等这些3的倍数，你有什么发现呢？

生：十位依次增加1，个位依次减小1。

师：你看到了其中的变化，有什么不变的东西吗？

生：各个数位上的数字加在一起是9。

（板书：个位与十位上的数字之和是9）

师：观察百数表里这些数每个数的数字之和，你发现它们有什么特别之处吗？生：这些数都是3 的倍数。

生：个位与十位上的数字之和是3 的倍数，这个数就是3 的倍数。

师：推想，如果一个数不是3的倍数，那会出现什么现象呢？

生：那么这个数的十位与个位上的数加在一起应该不是3 的倍数。

师：让我们看看百数表，找几个不是3 的倍数。

学生找到83、97、49 这些不是3 的倍数的数，请大家把它们的个位与十位上的数字加在一起。

生：83，8＋3＝11；97，9＋7＝16；49，4＋9＝13。11、16、13 不是3 的倍数。

（板书：个位与十位上的数字之和是：11、16、13，不是3 的倍数）

3.通过举例推广到三位数、四位数等。

师：刚才我们是举了两位数的例子，那么三位数呢？谁来举一个任意的三位数。

生：789，7＋8＋9＝24。

师：24 这个数是3 的倍数，我断定789 应当是3 的倍数。

生：569，5＋6＋9＝20。20 不是3 的倍数，我断定569 不是3 的倍数。

师：对789 和569 这两个数的判断，对不对呢？我们用计算器验证一下。

（组织学生用计算器来验证）

师：谁再来举个四位数？

生：5687，数字之和是26，26不是3 的倍数。

师：这个数是不是3 的倍数？

生：不是。

师：谁来稍微地改动一下，这个数就是3 的倍数了。

生：5697，数字之和是27，是3 的倍数。

（组织学生用计算器来验证）

师：我们举了一位数、两位数、三位数、四位数的例子，到目前为止，我们还没有找到反例。大家可能得出什么样的结论呢？

生：个位、十位、百位、千位上数字的和是3 的倍数，也就是各个数位上的数字之和是3 的倍数，这个数就是3 的倍数。

【设计意图：引导学生充分观察百数表中3 的倍数，归纳出3的倍数特征，然后分别举三位数、四位数的例子来进行验证，促进学生观察能力与归纳能力的提高，提升数学素养。】

4.证明规律，深化新知。

师：对比3 的倍数的特征与2、5 的倍数特征，你们有什么问题吗？

生：为什么3 的倍数不能只看个位，要看数位上的数字之和是否是3 的倍数呢？

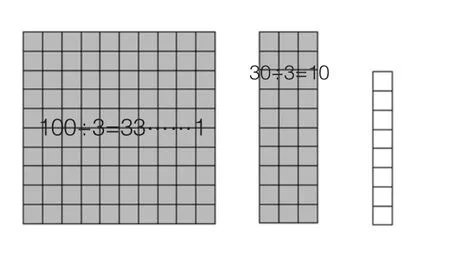
师：为什么3 的倍数特征要看各个位上的数字之和？谁来看图说一说，判断45 是不是3 的倍数，要看它的各个数位上的数字之和呢？小组讨论一下。

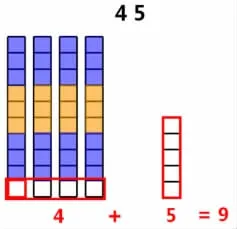
学生小组讨论后汇报：十位上的每一个10 除以3 以后余1，共余4，再加上个位上的5 一共是9，9 是3 的倍数，因此45 是3的倍数。

师：谁来看图说一说，判断123 是不是3 的倍数，只看个位行不行呢？要用1＋2＋3=6，6 是3 的倍数，才能说明这个数是3 的倍数吗？小组讨论一下。

学生小组讨论后汇报：百位上的100 除以3 以后余1，十位上的20 除以3 以后余2，再加上个位的3，一共是6，6 是3 的倍数，因此123 是3 的倍数。

师：判断123 这个数是不是3 的倍数，这里1 指100，但是当用1 去加的时候，还指的是1 吗？指的是什么呢？

生：指的是去掉99 以后剩下来的数。

师：用十位上的2 加的时候，这个2 指的是什么呢？

生：这个2 指的20 除以3 以后余下的2。

师：这就是为什么判断3 的倍数要看各个数位上数字之和的原因。

【设计意图：3 的倍数为什么有这样的规律是本节课深度学习的核心内容，延续2、5 倍数特征的证明方法，引导学生从数形结合的方式思考问题，学生基本能结合方格图说明为什么要用各数位上的数字加在一起，从数学证明的角度来看似乎不够严谨，但这就是儿童数学与抽象数学之间的区别，学生能通过形象的方式触摸到数学的本质，达到“非严谨”的直观理解。】

三、巩固规律，拓展延伸

1.及时巩固，劣实基础。

（做“练一练”第1 题与第2题）

师：在29、45、51、67、86、96中，哪些是3 的倍数呢？

（组织学生把3 的倍数圈出来）

2.你能很快说出哪几题的得数没有余数吗？

48÷3 56÷3 342÷3 567÷3 802÷3

提问：除数是3，得数没有余数是什么意思？

引导学生得出3 的倍数，除以3 没有余数；不是3 的倍数，除以3 就有余数。

3.同学们报名叠罗汉表演，现已有73 人报名参加了，如果三人一组，这73 人能不能都参加表演？至少再有几人报名，就都可以参加表演了？

4.从0、5、6、7 中选出三个数字，组成是3 的倍数的三位数，你能组成多少个？在这些数中哪些是2、3 的倍数？哪些是3、5 的倍数？哪些是2、3、5 的倍数？

提问：756 是2 的倍数，也是3 的倍数，如果改变一下数字的顺序，还是2 的倍数吗？还是3 的倍数吗？这说明了什么？

生：改动数位上数字的顺序不会影响它是3 的倍数。

5.在每个□里填一个数字，使组成的数是3 的倍数。你是怎样填的呢？有几种填法？

7□ □12 20□ 3□5

师：由72、75、78 你找到了一个什么规律呢？

生：确定第一个数字以后，只要依次增加3 就可以了。

6.优化拓展。

师：如果判断137 是不是3的倍数，还要用1+3+7 吗？

生：不需要了，因为十位是30，已经是3 的倍数了。

师：如果3 放在百位上呢？是317 呢？还要不要考虑呢？

师：是否一定要把所有数位上的数字加在一起呢？

生：这个3 放在十位、百位或者个位，它所代表的数一定是3的倍数，不需要把所有数位上的数字加在一起。

师：请大家判断96305363967、653 是不是3 的倍数。

生：96305363967 中 只要 看数字“5 和7”就行了。

生：653 中数字6 与3 已经是3 的倍数，只要看5 就行了。

【设计意图：通过层次练习使学生巩固了3 的倍数的判断方法，再次结合方格图引起学生思考如果一个数位上的数字所代表的数已经是3 的倍数，判断时不需要进行相加，优化了3 的倍数的判断方法，使学生更进一步理解了3 的倍数的特征。】

四、归纳概括、梳理总结

师：这节课你有哪些收获？这些收获是怎样获得的？

（学生回答略）

【课后反思：关于“3 的倍数”，苏教版教材是这样编排的：先是利用百数表，学生圈出3 的倍数，然后组织学生观察3 的倍数，发现这些3 的倍数的个位从0 到9 各种情况都有，个位上的数字没有规律，然后利用计数器拨出3 的倍数，引导学生发现各个数位上的珠子加在一起是3 的倍数。但是这样做没有使百数表得到充分地利用，其实通过观察百数表上圈出的3 的倍数，就可以非常自然地发现十位与个位上的数字之和是3 的倍数。如果再引入计数器，就显得有些突兀，多此一举了。充分利用百数表，组织学生观察，学生是能够探索出3的倍数特征的。学生在得出3 的倍数特征后会提出这样一个问题：为什么2、5 的倍数要用个位来判断，而3 的倍数则要用各个数位上的数字之和来判断。如果仅仅用例子归纳出来去说明“本就如此”，对学生来讲就失去了一次探究知识本质的机会。如果从数的组成来讲，在这节课中教师利用数形结合来说明其中的道理，并且与2、5 的倍数特征的算理沟通联系，有利于学生对于新知的深度把握，完成知识系统的构建。】