MHD角速度传感器微弱信号频率估计的互高阶谱方法∗
杨 乐,吴腾飞∗,纪 越,徐冲柯,杨凯丽,李醒飞
(1.天津大学精密测试技术及仪器国家重点实验室,天津300027;2.天津工业大学电工电能新技术天津市重点实验室,天津300387)
航天器在轨运行期间,受多种因素影响产生低幅值、宽频带的角颤振响应,称为空间结构微角振动[1]。微角振动会降低航天器指向精度和遥感分辨率等重要性能指标,严重时甚至危及航天器的安全[2]。磁流体动力学MHD(Magneto Hydro Dynamic)角速度传感器兼具高带宽、低噪声、小体积等优势,尤其适合空间结构微角振动的探测[3]。目前,MHD惯性传感技术及商品化仪器由美国ATA公司垄断。20世纪90年代,ATA公司Laughlin D R等人分别针对大量程[4]、改善低频特性[5]及降低噪声[6]等要求,提出了多种MHD角速度传感器设计方案。2015年ATA公司推出的低噪声型号ARS-14的等效噪声角速度低于5×10-6rad/s rms,-3dB 带宽为2 H~1000 Hz[7],代表了该领域的最高水平,但其相关技术及元件对中国封锁禁运,而国内在该领域的研究起步较晚。2014年,北京遥测技术研究所廉杰等人对传感器结构谐振频率特性和流体状态等进行分析,研制出带宽为5 H~500 Hz的传感器样机[8],并于2015年提出了一种MHD角速度传感器检测电路,抑制了零位偏置和零位温度漂移[9]。2011年兰州空间技术物理研究所周海佳等人仿真研究了MHD角速度传感器的磁场设计[10],并于2018年利用数值建模和实验方法研究MHD角速度传感器的灵敏度特性[11]。2013年至今,本课题组对MHD角速度传感器的传感模型[12]、结构设计[13]、测量误差[13]和磁场均匀性影响[14]进行了深入研究。MHD角速度传感器用于测量微小角振动,其最主要的性能指标是噪声和带宽[15],然而国外针对MHD角速度传感器的噪声特性研究发表论文很少,国内在此方面的研究较少。
根据磁流体动力学惯性传感原理,MHD角速度传感器低频截止频率由传感结构和材料特性决定[5],通常小于2 Hz,而高频截止频率由前置放大电路决定。目前MHD角速度传感器的研究集中于提高其低频信噪比以改善低频性能以及进一步降低通带噪声以获取更高的分辨力[12],因此MHD角速度传感器微弱信号提取是实现上述研究目标的关键问题。1994年,ATA公司的Pinney C等人讨论了MHD角速度传感器的噪声和漂移指标,但未进一步讨论噪声特性及噪声抑制方法[16]。2014年,本课题组将小波降噪方法用于MHD角速度传感器微弱信号参数估计,提高了输出信号信噪比[17]。2017年,本课题组使用卡尔曼滤波算法对MHD角速度传感器输出数据进行处理,有效提高了测量精度[18]。然而,上述研究未能根据MHD角速度传感器的噪声特性,针对性地选择信号参数估计方法。经过本文分析,MHD角速度传感器的噪声是一种有色高斯噪声。高阶统计量方法对高斯有色噪声有很强的抑制能力,理论上高斯噪声的四阶统计量为零[19]。近年来,国内外采用将高阶累积量与互功率谱估计相结合的互高阶谱方法,实现了有色高斯噪声背景下的正弦信号频率估计[20]、指数信号参数估计[21]、谐振信号恢复[22]及故障诊断[23]。上述研究表明互高阶谱估计方法可以有效抑制有色高斯噪声,提高信噪比。
本文采用互高阶谱估计方法对MHD角速度传感器噪声背景下的微弱信号进行频率估计。首先介绍MHD角速度传感器的工作原理,并通过实验分析了MHD角速度传感器输出信号的噪声背景特性。然后采用三种常用的互高阶谱估计方法对MHD角速度传感器低信噪比输出信号进行频率估计,分析了各种算法在不同频率范围内,不同信噪比下的性能。最后对MHD角速度传感器噪声背景下的微弱信号参数估计方法进行了总结和展望。
1 MHD角速度传感器工作原理及噪声分析
1.1 MHD角速度传感器工作原理
图1为MHD角速度传感器工作原理图,导电流体灌装于环形封闭通道内,通道上下表面绝缘,内外表面导电,与壳体相连的永磁体或通电线圈产生磁场B。MHD角速度传感器利用导电流体在旋转磁场中切割磁感线产生电动势的原理测量角速度,当壳体以角速度ω旋转时,永磁体和导电流体通道相对惯性空间产生角位移,而导电流体惯性较大,相对于惯性空间几乎静止,导电流体与磁场间产生相对速度vq。导电流体切割磁感线,在通道的内外壁之间产生与角速度ω成正比的感应电动势E,如式(1)所示[17]:

式中:B为外磁场磁感应强度(T);W为流体通道有效宽度,即W=ro-ri(m);r为半径均方根,即(m);v为运动粘度(m2/s);h为通道高度(m);H 为Hartmann常数,H=Bh/ ρvη(无量纲);ρ为导电流体密度(kg/m3);η为导电流体电阻率(Ω·m)。

图1 MHD角速度传感器工作原理示意图[4]

图2 MHD角速度传感器幅频相频曲线
MHD角速度传感器幅频相频曲线如图2所示,从图中可以看到MHD角速度传感器具有良好的高频特性,因此主要用于测量微小角振动信号,而其低频特性较差,因此无法测量稳定的姿态角和恒定转速。
1.2 MHD角速度传感器噪声特性分析
图3所示为MHD角速度传感器噪声分析系统,被测角振动信号由Acuitas TES-3V_AB转台产生,实验中该转台工作在角振动模式,角振动的频率和幅值由转台控制软件设置。MHD角速度传感器通过工装紧固在转台正中心,感应转台输出的角振动信号,转换为电压信号输出。使用NI PCI-6289采集卡采集MHD角速度传感器输出信号,考虑到传感器高频截止频率约为500 Hz,为测量整个通带内的噪声功率谱密度,取采样频率Fs=5 000 Hz,为观察1 Hz以下功率谱密度曲线,取采样时间T=10 s。数据采集完成后使用MATLAB对数据进行处理。
图4(a)所示为由PCI-6289采集到的MHD角速度传感器噪声分析系统总噪声功率谱密度曲线和PCI-6289的本底噪声功率谱密度曲线,系统总噪声包含了MHD角速度传感器自身的噪声和采集卡的本底噪声。采集卡本底噪声远小于系统的总噪声,因此本文将PCI-6289采集到的系统总噪声视为MHD角速度传感器噪声。

图3 MHD角速度传感器噪声分析系统
MHD角速度传感器前置电路包含积分反馈环节,用于抑制直流失调,使得传感器的低频截止频率为0.4 Hz。因此小于0.4 Hz时,MHD角速度传感器噪声特性由电路高通性能与1/f噪声共同作用;0.4 Hz到1 Hz,主要受1/f噪声影响;1Hz到500 Hz主要受白噪声影响。由图4(a)可知噪声功率谱不平坦,因此MHD角速度传感器的噪声属于有色噪声。噪声样本均值为1.001 7×10-4V,标准差为0.002 1 V。 原样本与构造样本概率密度曲线对比如图4(b)所示,原样本符合正态分布,原样本为MHD角速度传感器噪声,构造样本为以上述均值和方差构造的正态分布序列,因此MHD角速度传感器的噪声属于高斯有色噪声。
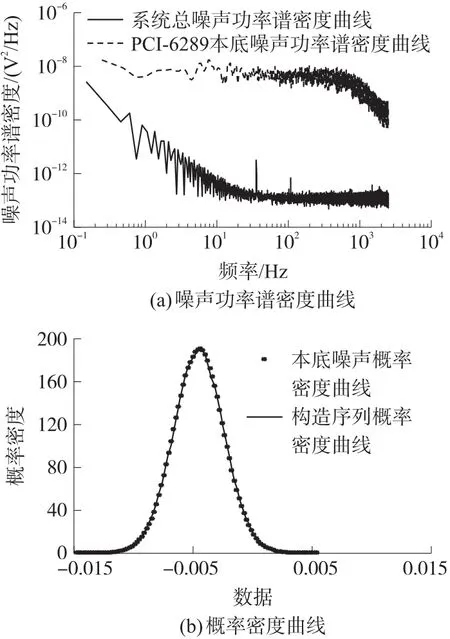
图4 MHD角速度传感器噪声特性分析
根据上述噪声特性分析,MHD角速度传感器输出信号可视为正弦信号与高斯色噪声叠加[31]
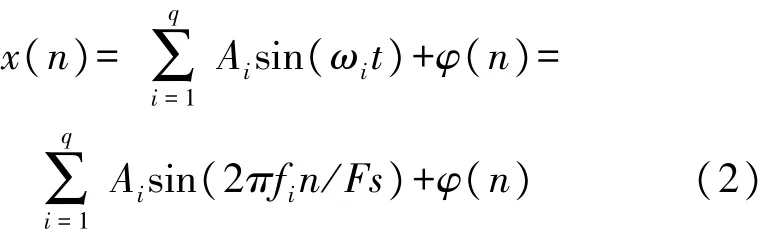
式中:n为采样点序号,n=1,2…N,N 为序列长度;t为时间刻度,t=n/Fs,Fs为采样频率,1/Fs为相邻两点的时间间隔;q 为正弦信号个数;Ai、fi、ωi分别为第 i个正弦信号的振幅、频率、角速度,i=1,2…q;φ(n)为高斯色噪声。
2 基于四阶累积量的互高阶谱估计方法
经典谱估计性能受限于数据长度,短数据无法获得良好性能,现代谱估计虽不受限于数据长度且对互不相关噪声有很强的抑制能力,但对相关噪声抑制效果很差[19]。高阶统计量中应用较广泛的是四阶累积量,与现代互谱、MUSIC算法和Esprit-Tls算法相结合,形成互四阶谱算法[24]、互四阶MUSIC算法[25]和互四阶Esprit-Tls算法[26],可以对各种互不相关和相关噪声起到抑制作用,因此可以有效提取高斯色噪声背景下的微弱信号。
设x(n)和y(n)均为带有高斯色噪声的正弦信号,如式(2)所示,则x(n)和y(n)的互四阶累积量为[25]

令 cxy(m)= cxyyy(m,0,0)= E[x(n)y(n+m)y(n)y(n)],x(n)和y(n)的互四阶谱为[19]互四阶累积量矩阵记为Cxy,即

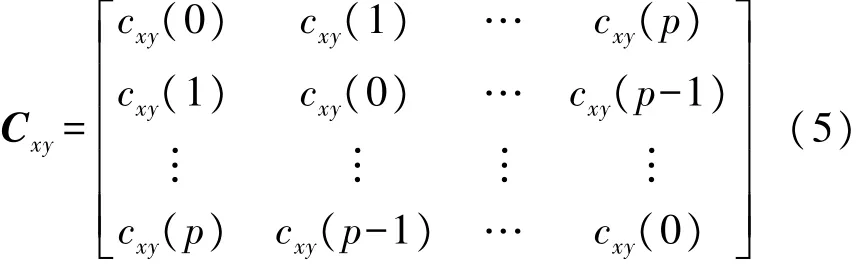
对 Cxy进行奇异值分解,U=[u1,u2,…up],V=[v1,v2,…vp]分别为其左右奇异矩阵,互四阶MUSIC算法即通过计算下式极大值估计信号频率。
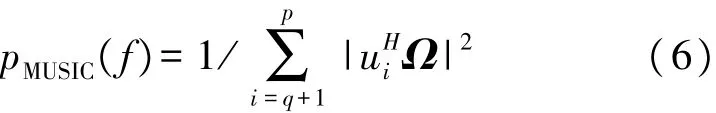
式中:Ω=[1,ej2πf,e2j2πf,…,epj2πf]。
令x(n)和y(n-1)的互四阶累积量矩阵为Cxy′。对 Cxy进行广义特征值分解,令 U1=[u1,u2,…uq],V1=[v1,v2,…vq],用 UH1左乘和用 VH1右乘矩阵 Cxy-γCxy′,可得 Σ-γUH1Cxy′V1,γ 为{Cxy,Cxy′}广义特征值,Σ 是Cxy非零奇异值矩阵。互四阶Esprit-Tls算法即通过求解{Σ,γUH1Cxy′V1}的广义特征值来估计频率[26]。
3 仿真及实验
3.1 仿真和实验条件
为评估MHD角速度传感器微弱信号频率估计的互高阶谱方法的性能,本文采用式(2)所示的信号和噪声关系和MHD角速度传感器实验测量数据来验证算法的性能。仿真数据由MATLAB产生,根据信噪比调整噪声功率大小。实验中通过控制软件驱动转台产生不同频率、不同幅值的被测正弦角振动。MHD角速度传感器感应角振动,转换为正弦电压信号由PCI-6289采集。根据图2所示MHD角速度传感器频率特性曲线和转台最高稳定振动频率,实验中被测角振动的频率和不同信噪比下的幅值如表1所示。根据表1所列待测振动频率,取采样频率Fs=2 000 Hz,采样点数N=2 000,采样时间T=1 s。所采用的互四阶MUSIC、互四阶Esprit-Tls算法中互四阶矩阵阶数M=500,仿真及实验均重复10次求平均。实验数据信噪比单位为分贝,由以下公式计算

表1 实验中被测角振动频率和幅值

式中:SNR为信噪比,Ps和Pn分别代表信号和噪声的有效功率。
算法频率估计分辨力Δf定义为算法恰能分辨出的频率间隔,设S(f)为频率f处的功率谱密度,若,则算法恰能分辨出待测频率f1和f2,则分辨力为

此外,本文对不同算法的频率估计的偏差和方差进行了比较分析。
3.2 不同频段下的频率估计性能比较
比较经典谱估计中的BT法和互高阶谱估计在不同频段的频率估计的分辨力、偏差和方差。
首先比较不同算法的频率估计分辨力。图5为信噪比为0 dB时,各算法的归一化功率谱估计密度,取待测频率为40 Hz和41.5 Hz举例说明。由图中可知,互四阶谱算法可以很好地分辨出两个待测频率,互四阶MUSIC算法虽能分辨出待测频率,但是已达到分辨力极限,而BT法和互四阶Esprit-Tls算法不能分辨出待测频率。

表2 不同频段各算法的频率估计分辨力(信噪比0 dB)
为全面分析上述算法的频率估计特性,表2给出信噪比为0 dB时各算法在不同频段的分辨力。由表2可知,BT法的频率估计分辨力明显不及其他方法。其他三种算法,在不同的频段下,其频率估计的分辨力基本保持稳定。互四阶MUSIC算法和互四阶Esprit-Tls算法的频率估计分辨力较为接近,而互四阶谱算法的频率估计分辨力明显好于上述两种算法。
图6和图7为信噪比为0 dB时,各算法对仿真和实验数据频率估计的偏差和方差,各算法对仿真与实验数据的处理结果相近。比较对仿真和实验数据的频率估计偏差,互四阶谱和互四阶MUSIC算法优于BT法和互四阶Esprit-Tls算法,估计值与真值相差较小。四种方法中,互四阶Esprit-Tls算法频率估计方差最大,估计值波动性较大,其余方法方差接近。综合考虑频率估计的偏差和方差,互四阶谱算法和互四阶MUSIC算法性能最好。

图5 40 Hz附近的各算法的分辨力(信噪比0 dB)

图6 不同频率仿真数据频率估计的偏差和方差(信噪比0 dB)
3.3 不同信噪比下的算法性能比较
比较BT法和互高阶谱估计算法在不同信噪比时的分辨力、偏差和方差。图8为信噪比-2 dB时40 Hz附近各算法的频率估计分辨力,图中待测频率为40 Hz和41.6 Hz。互四阶谱算法和互四阶MUSIC算法都可以地分辨出两个待测频率,但互四阶MUSIC算法已达分辨力极限,而BT法和互四阶Esprit-Tls算法则不能分辨出待测频率。

图8 40 Hz附近各算法的频率分辨力(信噪比-2 dB)
各算法在不同频率下的频率估计分辨力很稳定,因此本文计算不同信噪比表2所列五个频率的频率估计分辨力的平均值,如表3所示。

表3 不同信噪比下各算法的频率估计分辨力
各算法的频率估计分辨力随信噪比升高有所改善。互四阶MUSIC算法和互四阶Eprit-Tls算法在信噪比低于-3 dB时已不能有效分辨出待测频率,所以只给出-3 dB以上频率估计分辨力。BT法虽然可以在信噪比为-5 dB时使用,但分辨力较差。互四阶谱算法可以在信噪比为-5 dB时分辨出待测频率,互四阶谱算法的频率估计分辨力<1 Hz,分辨力明显好于其他三种算法。
图9和图10分别为不同信噪比下各算法对仿真和实验数据频率估计的偏差和方差。受实验设备条件限制,实验数据信噪比最低只能取到-3 dB,所以仅给出-3 dB以上的频率估计偏差和方差。由于各算法在不同频率下的频率估计的偏差和方差较稳定,因此图中数据为表2所列五个频率的频率估计偏差和方差的平均值。互四阶谱算法和互四阶MUSIC算法的频率估计偏差和方差都较小,频率估计偏差达到10-15V,频率估计方差达到 10-30V2。
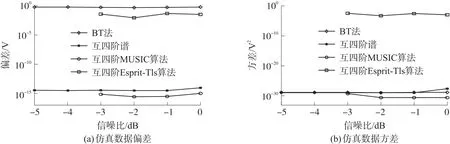
图9 不同信噪比仿真数据频率估计的偏差和方差

图10 不同信噪比实验数据频率估计的偏差和方差
为进一步分析互高阶谱频率估计性能,本文分析不同算法对信噪比的改善。由于互四阶Esprit-Tls算法仅给出频率信息,无法给出信号强度,因此图11所示为实验数据经其他三种算法处理后的信噪比。三种算法处理后数据信噪比均上升,互四阶MUSIC算法在不同频率下远优于BT法,信噪比可以提升7 dB~11 dB,而互四阶谱算法对信噪比的改善程度略优于BT法。

图11 实验数据处理后信噪比变化
4 总结
本文对MHD角速度传感器噪声背景进行了分析,并根据其噪声特点提出使用四阶累积量与现代互谱相结合的互高阶谱频率估计方法对信号进行处理。在不同频率和信噪比下,对仿真和实验数据的处理结果表明,互四阶谱算法和互四阶MUSIC算法具有较好的频率估计偏差和方差。在要求高频率分辨率的情况下,可以选用互四阶谱算法,而互四阶MUSIC算法可以在低的信噪比环境下使用,两种算法对高斯有色噪声均具有有效的抑制作用。相比经典谱估计方法,互高阶谱方法更加适用于MHD角速度传感器高斯有色噪声背景下的微弱信号频率估计。

