基于格的无线传感器网络密钥协商协议∗

王淑华，陈振龙

(1.浙江工商大学统计与数学学院，杭州310018；2.绍兴文理学院数理信息学院，浙江 绍兴312000)

无线传感器网络WSN(Wireless Sensor Networks)集微电技术、传感器技术、通信技术于一体，可广泛应用于教育、军事、医疗、交通等诸多领域，拥有巨大的应用潜力和商业价值，引起了国内外广泛的关注和研究[1－5]。安全问题是无线传感器网络不得不考虑的一个重要问题，本文主要探讨的是无线传感器网络的密钥协商问题。除现有无线传感器网络本身存在的安全问题，如由于无线链路媒体的开放性、终端的移动性、动态变化的网络拓扑结构、协作算法、缺乏集中监视和管理点以及没有明确的防线，使得无线传感器网络容易遭到各种各样的攻击，如数据窃听、信息窜改、恶意跟踪等。未来的无线传感器网络，由于网络的复杂性、管理的复杂性，使得其要面临更复杂的安全问题。以提供安全、可靠的信息通信为目标的密钥协商是无线传感器网络安全研究最为重要、最为基本的内容，有效的密钥协商协议也是其他安全机制，如安全路由、安全定位、安全数据融合及针对特定攻击的解决方案等的基础。相对于传统网络，无线传感器网络更易受到包括被动窃听、数据篡改和重发、伪造身份、拒绝服务、节点俘获等安全威胁和攻击，使得这些研究成果一般不能直接应用于无线传感器网络。虽然无线传感器网络在现今信息技术领域是一个研究热点，但绝大部分研究都集中于无线传感器网络的互联技术，而对无线传感器网络的密钥协商协议的研究较少[6－9]。因此，如何保证无线传感器网络安全是无线传感器网络研究领域里的一项极其重要内容。为了解决无线传感器网络通信存在的安全性问题，需要设计兼具安全性和有效性，并且适用于无线传感器网络的的密钥协商协议。

随着量子计算与量子计算机的研究与发展，逐渐发现目前传统的非对称密码体制所使用的难解问题将不再安全[10－14]。1997年，贝尔实验室的Shor提出了分解大整数和求解离散对数的量子算法，并在文献[13]中证明了其运算的时间复杂度是多项式级别的。利用量子计算机可以攻破经典的DSA体制，RSA密码体制，ECC体制等非对称密码体制。因此，研究量子计算机环境下安全的非对称密码体制是非常重要的，并且已经成为当前信息安全与密码学界研究的重点方向与热点。后量子时代的安全性已经成为信息安全与密码学家重点关注的问题。格公钥密码作为后量子计算机时代非对称密码体制的典型代表，在密码学领域内占居着非常重要的地位[15－21]。

无线传感器网络部署后，所有节点需要在密钥协商后才能参与通信，新的节点要想加入网络也必须通过密钥协商才能获得其他节点认可。目前，针对无线传感器网络的密钥协商协议可分为两大类：基于对称密码体制和基于非对称密码体制。当传感器节点能量被耗尽或者被确认为非法节点，网络必须及时清除淘汰该节点，传感器节点之间的密钥协商用以保证通信传感器节点的合法性，是无线传感器网络安全通信的前提。基于对称密码体制的密钥协商协议存储消耗大，抗捕获能力差；而基于非对称密码体制的密钥协商协议计算消耗大，拓展性、健壮性差。大量已有研究工作致力于减小非对称密码体制的计算开销与能耗；提出更为安全、合理的密钥协商协议。鉴于以上问题，本文提出了一种有效的无线传感器网络密钥协商协议。有关无线传感器网络密钥协商协议可以参考无线传感器网络相关安全问题的综述等[22－24]。

利用格上坚实的安全基础和更高的计算效率，本文提出一种基于格的无线传感器网络密钥协商协议，通过概率输出认证信息，使输出认证信息的分布与认证主体的私钥无关。节点之间只在需要通信时才建立相应配对密钥，能相互验证密钥的有效性，仅需较少步骤就能够以很高的概率进行密钥协商。建立的配对密钥是基于对称密码体制，这样通信的效率会提高很多。

1 基础知识

1.1 格

定义1 在m维向量空间Rm中取n(m≥n)个线性无关的向量 b1，b2，…，bn∈Rm，定义由这 n 个向量生成的格为：

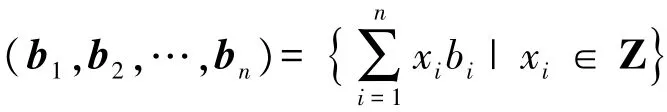
式中：向量 b1，b2，…，bn称为格的基。 若定义 m×n维矩阵 B，其列向量分别为 b1，b2，…，bn，则由矩阵B生成的格可以定义为：

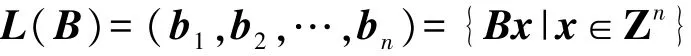
式中：n称为格的秩；m称为格的维数；m＝n的格被成为满秩格。

1.2 格上的难解问题

格上的难解问题主要有最短向量问题(SVP)、最近向量问题(CVP)、最短独立向量问题(SM)等。另外，一般加密有关的方案安全性基于错误学习(LWE)问题，签名相关方案的安全性基于小整数解(SIS)问题。下面给出部分问题的具体定义。

定义2 最短向量问题SVP(Shortest Vector Problem)问题：给定秩为n的格L(B)⊆Zm的一组基B，找到一个非零向量u∈L(B)，使得对格上的任意向量v∈L(B)满足如下条件：

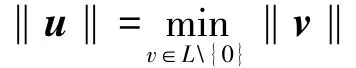
有些格上的最短向量不一定是唯一的，比如：如果u是一个最短向量，那么－u也同样是一个最短向量。1981年，Boas在文献[16]中证明了最短向量难解问题在ℓ∞范式下是NP难解问题。1998年，Ajtai等人在文献[17]中证明了最短向量问题在ℓ2范式下是NP难解问题。

定义3 最近向量问题CVP(Closest Vector Problem)问题：给定秩为n的格L(B)⊆Zm的一组基B和一个目标向量x∈span[L(B)]，找到一个满足如下条件的非零向量u∈L(B)：

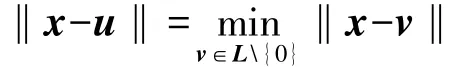
在文献[20]中，Henk通过归约的方式证明了最近向量难解问题比最短向量难解问题更难。另外，Boas在文献[16]中也证明了最近向量难解问题是NP难解问题。

定义4 小整数解问题SIS(Small Integer Solution)问题：给定一个正整数q，一个随机矩阵A∈Znq×m和一个实数 β＞0，定义(q，m，β)小整数解问题表述如下：找到一个非零向量v⊆Zm，使得Av＝0(modq)，并满足‖v‖≤β。

SIS问题的难解性：对任意的m(n)＝Θ(nlogn)，存在一个q(n)＝O(n2logn)使得对任意函数γ(n)＝ω(nlogn)，以不可忽略的概率解决平均情况的 SISq，n，m，β问题至少和解决最坏情况的SVPγ一样难解[18]。

1.3 格上的相关算法

抽样技术首先是由 Gentry，Peikert和 Vaikuntanathan在文献[10]中提出的，是格非对称密码体制发展过程中出现的一种非常重要的技术，许多格上的非对称密码体制协议都使用了抽样技术。

定理1(陷门生成算法) 令q≥3是一个素数，m＝「6nlogq⏋。存在一个概率多项式时间算法TrapGen(q，n)输出矩阵对：

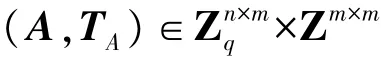
式中：A 的分布和 Zn×mq上的均匀分布统计接近，TA是 q－ary格 Λ⊥q(A)上的一组短基，同时如下两式以压倒性的概率成立：

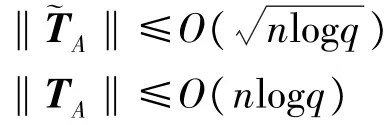
2012年，Micciancio和Peikert在文献[14]中提出了格上的新陷门(G－陷门)：

定理2(G－陷门生成算法) 给定矩阵A∈Znq×m，T∈Zmq0×kn和 M∈Znq×n，其中 n，m，m0，k 是正整数。如果满足如下等式：

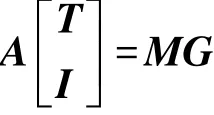
并且‖T‖足够小，那么T就是A对于标签M的G陷门。

由于Gentry等人在文献[10]中的抽样技术计算较为复杂，Lyubashevsky在文献[12]中提出了一种基于格的无需原像抽样操作的技术。

2 网络模型

在本文提出的密钥协商协议中，采用无线传感器网络标准模型进行密钥预分配管理。无线传感器网络由基站和普通节点两种类型构成，并有如下假设：①传感器节点的密钥对都是由基站生成并预分配给所有传感器节点，传感器节点之间也可以进行通信。②每个传感器节点都有自己唯一的身份标识IDi∈{0，1}∗，i∈{1，2，…，N}。 ③在本文提出协议中的基站存储够用，而且是诚信可靠的。

无线传感器网络的拓扑结构如图1所示。

在图1中，基站具有无限能量、高计算能力以及充足的存储空间等特点，并且是诚信可靠的。传感器节点C的功能是负责感知周围环境，将采集到的数据发往基站，如果太远也可以选择其他传感器节点进行转发。

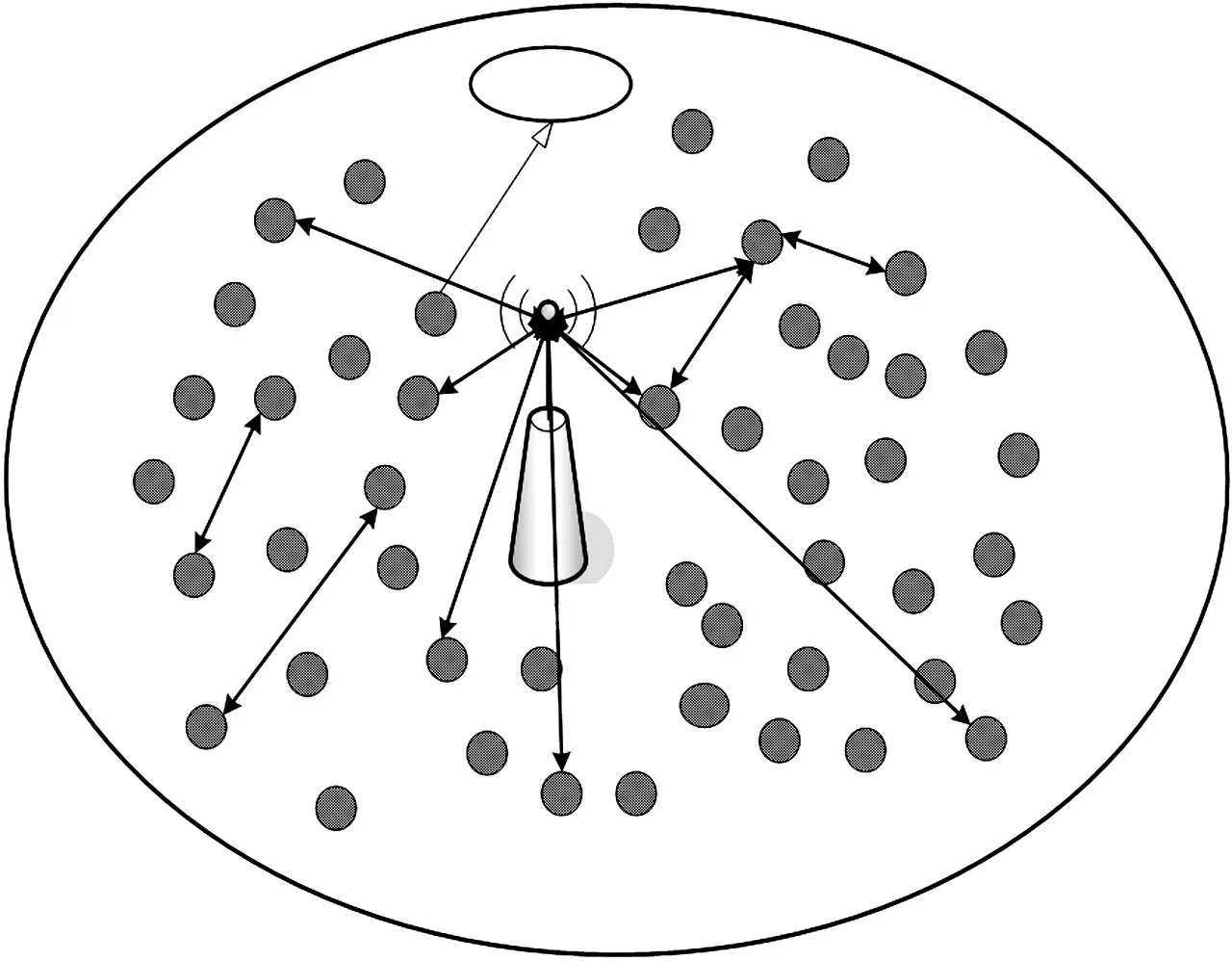
图1 网络模型

3 密钥协商协议

根据文献[12]中的无需抽样操作技术和文献[25]中的消息恢复算法，本文提出了一种基于格的无线传感器网络密钥协商协议，采用无线传感器网络基本的密钥预分配模型，基站首先生成系统参数和所有传感器节点的公私密钥对，并把密钥对分配给相应的传感器节点。传感器节点之间只在需要通信时才建立相应配对密钥，仅需较少步骤，就能够以很高的概率进行密钥协商。建立共享密钥后相关传感器节点就可以用该共享密钥进行安全通信，该共享密钥是基于对称密码体制的。由于对称密码体制比非对称密码体制在加密运算中效率更高，所以能有效降低传感器节点的通信能耗。

3.1 系统参数和密钥对

系统参数和密钥对的产生如下：

①令系统安全参数是1n。

②首先选择素数 q，正整数 d，m，k，λ，l，其中 m必须满足如下不等式：

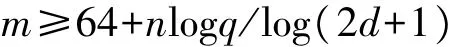
选择实数σ，满足如下不等式：

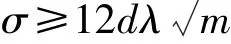
③选择一个随机矩阵A∈Zn×mq。

④选择四个安全的哈希函数：

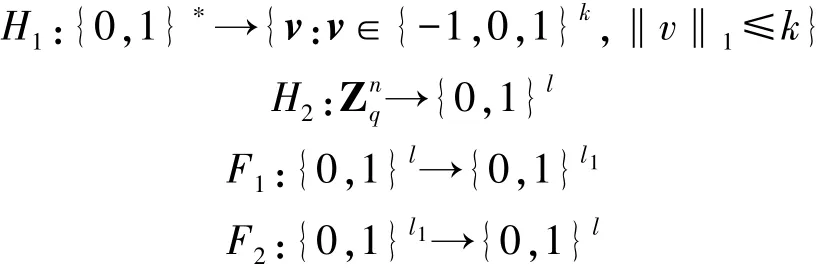
⑤生成传感器节点的密钥对，首先随机选择矩阵Si为第i个传感器节点的私钥，则Ti＝ASi为第i个传感器节点的公钥，其中Si满足如下条件：

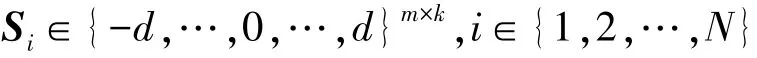
最后，输出系统公共参数：

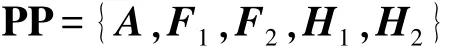
传感器节点的密钥对：

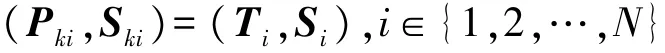
3.2 生成临时会话密钥

如果有传感器节点要与其他传感器节点进行通信时，该传感器节点首先生成相应的密钥协商消息，然后把生成好的密钥协商消息发送给相应的传感器节点。当其他传感器节点收到密钥协商消息后，先进行验证，如果通过验证，则接收相应的密钥消息，否则拒绝接收或丢弃该密钥协商消息，密钥协商的详细过程如下：

输入系统公共参数 PP＝{A，F1，F2，H1，H2}，假设第i个传感器节点需要与第j个传感器节点进行通信时，第i个传感器节点将随机产生一个用于本次通信的临时会话密钥Kij：Kij∈{0，1}l，该密钥为对称密码体制下的密钥，使用对称密码体制进行加解密效率更高。密钥协商数据包生成的具体过程如下：

①选择一个随机的 y：y←Dmσ和时间戳 ti：ti∈{0，1}∗，其中ti表示该认证消息是第i个传感器节点在t时刻生成的。

②计算uy和uK：

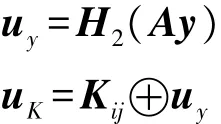
③计算 u′K：

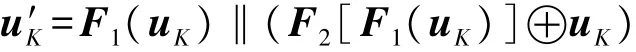
④计算验证消息(z，c)：

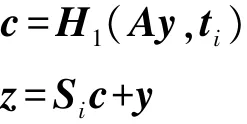
⑤以概率个传感器节点把包含临时会话密钥的消息(z，c，u′K，ti)发送给第j个传感器节点。

其中时间戳ti用于判断数据包的时间有效性和是否被重复接收；(z，c)用于验证；u′K用于验证后提取临时会话密钥的消息。输出(z，c)，第 i

3.3 验证并恢复临时密钥

当第j个传感器节点收到第i个传感器节点发送过来的消息(z，c，u′K，ti)时，首先用第 i个传感器节点的公钥Ti验证该消息的有效性，如果验证通过，就提取并接收第i个传感器节点发送过来的临时会话密钥，并用该会话密钥与第i个传感器节点进行通信，验证失败，则丢弃该数据包。具体的验证恢复过程描述如下：

①验证下面两个式子是否都成立：

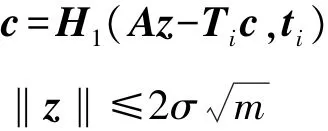
如果以上两式都成立，则表示验证通过，将继续下一步操作；否则验证失败，并丢弃这个由第i个传感器节点发送过来的数据包。

②计算：

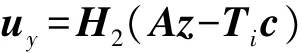
③恢复消息uK：

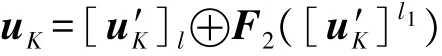
④验证等式[u′K]l1＝F1(uK)是否成立，如果成立，则恢复将与第i个传感器节点进行通信的临时会话密码 Kij：Kij＝uK⊕uy；如果失败，则丢弃该数据包，并终止操作。

其中[u′K]l1表示：u′K中从高到低的前 l1位；[u′K]l表示：u′K中从低到高的后 l位。

最后，第j个传感器节点接收到第i个传感器节点发送过来的临时会话密钥信息，如果通过验证就能从该数据包中恢复出与第i个传感器节点进行通信的临时会话密钥Kij。

如果基站发现有传感器节点被俘获，要及时把该节点的ID信息广播出去，避免其进行恶意攻击。

3.4 使用临时密钥通信

当第j个传感器节点恢复出临时会话密钥Kij后就可以与第i个传感器节点进行安全通信，下面介绍两种通信方式，可以根据具体情况选择不同的通信方式。

①直接用恢复出的对称密钥进行通信

第j个传感器节点：

加密消息u：

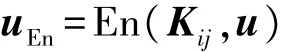
式中：u表示需要加密的消息；Kij表示：第j个传感器节点和第i个传感器节点的临时会话密钥；En(Kij，u)表示：用临时会话密钥Kij对需要加密的明文消息u进行加密，使用的算法为效率较高的对称密码体制算法，设该算法为E-SYM；uEn表示：加密后的密文消息。接着，第j个传感器节点将加密后的密文uEn发送给第i个传感器节点。

当第i个传感器节点接收到由第j个传感器节点发送过来的密文uEn后，将用之前生成的临时会话密钥Kij对uEn解密。

第i个传感器节点：

解密消息：

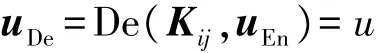
式中：De(Kij，uEn)表示：用临时会话密钥Kij使用对称密码体制算法E-SYM对密文uEn进行解密；uDe表示解密后的密文消息。最后，第i个传感器节点就获取了由第j个传感器节点发送过来的消息u：u＝uDe。

②把密文嵌入到验证消息后进行通信

第j个传感器节点：

(a)加密消息u：

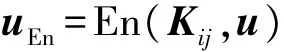
(b)计算密文嵌入后的消息(zj，cj)：

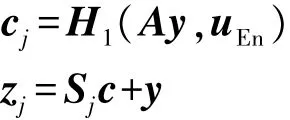
(c) 以概率的消息(zj，cj)。

接着，第 j个传感器节点把消息(zj，cj，uEn)发送给第i个传感器节点。

当第i个传感器节点接收到由第j个传感器节点发送过来的包含密文的消息(zj，cj，uEn)后，将用第j个传感器节点的公钥Tj验证消息(zj，cj)，验证通过后，将用之前生成的临时会话密钥Kij对uEn解密。

第i个传感器节点：

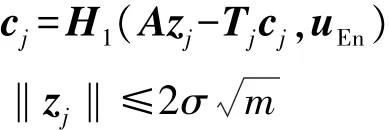
如果以上两式都成立，则表示验证通过，将继续下一步操作；否则验证失败，并丢弃这个由第j个传感器节点发送过来的数据包。

(b)解密消息uEn：

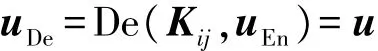
最后，第i个传感器节点就获取了由第j个传感器节点发送过来的消息u：u＝uDe。

以上所述两种通信方式各有优缺点，可以根据具体情况选择不同的通信方式。如果要加密的文明数据量很大，安全级别要求不是很高的情况下，可以使用第一种通信方式，该通信方式只要用对称密码体制算法E-SYM进行加解密操作即可，该通信方式效率更高；如果要加密的数据量不是很大，安全级别要求较高的情况可采用第二种通信方式，该方式可以避免其他传感器节点冒充第j个传感器节点与第i个传感器节点通信，该通信方式安全性更高。

另外，根据无线传感器网络的具体安全环境情况，可以适当改变临时会话密钥的有效时间，减少密钥协商的次数，提高无线传感器网络通信的效率。

4 协议分析

本文从一致性、安全性和效率3方面对新方案进行分析。

4.1 一致性

按照上述密钥协商协议的具体过程，本文对验证过程一致性和密钥恢复一致性分别进行阐述和分析。

①验证过程一致性分析：

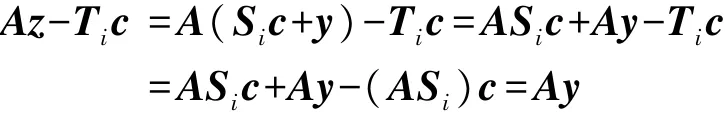
所以：

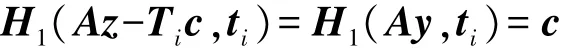
在证明以压倒性概率满足‖z‖≤2σ m不等式成立之前先介绍下面两个引理：

引理1[12]对任意实数σ＞0和正整数m，有如下不等式成立：

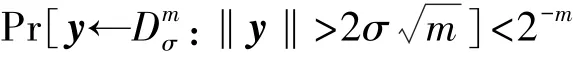
引理2[12]对任意的向量v∈Zm，如果：

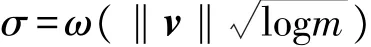
则有如下等式成立：

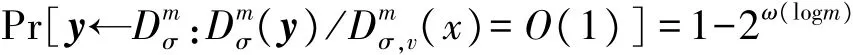
根据文献[12]中所述的无需原像抽样技术的原理和引理1得出，z的分布非常的接近Dmσ；由引理2可以得出z将以大于或等于1－2－m的概率满足不等式‖z‖≤2σ m，即以压倒性概率满足不等式‖z‖≤2σ m。

②密钥恢复一致性分析：

(a)分析等式[u′K]l1＝F1(uK)：

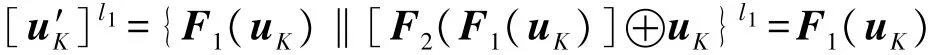
(b)对密钥Kij的正确性进行分析：

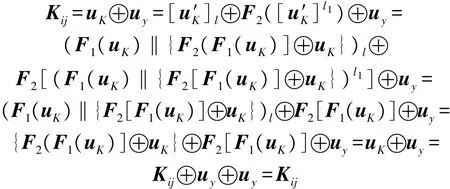
从以上分析可以得出，第i个传感器节点和第j个传感器节点拥有共同的对称密码体制算法E-SYM的密钥Kij，并能用Kij进行通信。

4.2 安全性分析

本节分析上述密钥协商协议在参数为[q，m，(4σ＋2dλ) m]的小整数解问题假设下是安全的，下面分别从密钥协商过程和传感器节点通信两方面进行安全分析。

①密钥协商协议安全分析

由4.1节中的定义4可得，参数为[q，m，(4σ＋2dλ)的小整数解问题具体表述如下：

给定一随机矩阵 A∈Znq×m和一个实数(4σ＋2dλ) m＞0，找到一个非零向量 v⊆Zm，使得 Av＝0(modq)，并满足‖v‖≤(4σ＋2dλ) m。

首先构造一个多项式时间算法ξ，并假设算法ξ以不可忽略的概率得到消息一个新的伪造认证签名(z∗，c∗)，使得：

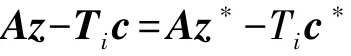
由于 Ti＝ASi，则：

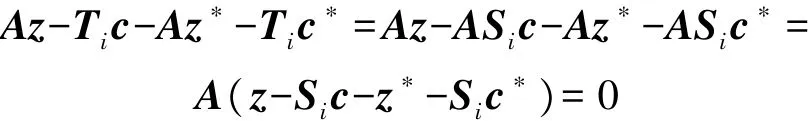
根据密钥协商消息的一致性可得：‖z‖，‖z∗‖≤2σ m和‖Sic‖，‖Sic∗‖≤dλ m以压倒性概率成立，则：

所以只要证明 z－Sic－z∗＋Sic∗≠0的概率是不可忽略的就能说明该密钥协商协议是安全可靠的。

在继续证明之前先介绍引理3。

引理3[12]对于满足条件m≥64＋nlogq/log(2d＋1)的任何矩阵 A∈Znq×m，随机选取d}m，那么以1－2－m的概率存在另外一个 s′：s′∈{－d，…，0，…，d}m，满足 As＝As′。

根据上面引理3可以得出，能比1－2－m大的概率生成一个新的传感器节点私钥S′i满足等式ASi＝AS′i。 则：

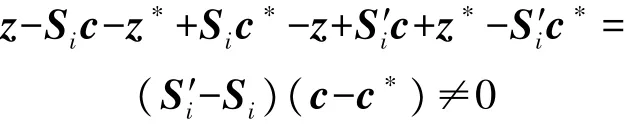
则有：

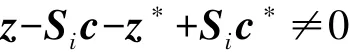
因此，本文提出的密钥协商过程在参数为[q，m，(4σ＋2dλ)的小整数解问题假设下是安全的。

②传感器节点通信安全分析

如果在第i个传感器节点和第j个传感器节点进行密钥协商的过程中没有其他恶意传感器节点窃听，那么第3节中所述的第1种直接用临时会话密钥Kij进行通信的方案是安全的。

如果在第i个传感器节点和第j个传感器节点进行密钥协商的过程中有恶意传感器节点e窃听到该密钥协商数据包，恶意传感器节点e就可以通过第i个传感器节点的公钥Ti验证并恢复出临时会话密钥Kij，这种情况只能采用第2种把加密消息嵌入到验证消息的方案进行通信，下面分析第2种通信方式的安全性。

恶意传感器节点e可以冒充第j个传感器节点对消息“u”进行加密并生成密文“uEn”：“uEn”＝En(Kij，“u”)；但由于传感器节点 e并不知道第 j个传感器节点的私钥Sj，所以没办法把冒充的密文“uEn”嵌入到验证消息zj中：

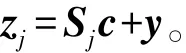
从以上的分析中可以看出本文提出的第i个传感器节点和第j个传感器节点用临时会话密钥进行通信的方案是安全的。

4.3 性能分析

下面首先将对提出方案的安全性、计算量和量子攻击等方面与其他相关方案进行比较。其中文献[5]涉及到的是指数级计算，在GDH(Gap Diffie-Hellman)假设下，达到了认证安全性，虽然它们在较强安全模型下具有较高的安全性，但是容易遭到量子攻击，而本文提出的方案是基于格的，所以只涉及到矩阵和向量的乘积运算，没有涉及到指数运算，这样计算简单，效率高，由于基于格的小整数解问题能够抵抗量子攻击，因此本文提出的方案有较高的安全性和效率。文献[15]提出的认证密码方案由于是基于理想格，这就导致其在效率方面会比本文提出的方案要稍微弱些，但在安全证明等方面会比较好些，这也是本文提出的方案需要进一步改进和完善的地方。文献[7]使用了密钥封装技术，这导致该密钥协议具有较大的存储空间和计算量，本文提出的方案没有使用对应的密码方法对签名和密钥等封装来进行认证，因此相比文献[7]更具有较小的存储空间和计算量。性能比较如表1所示。

表1 相关方案的性能比较

从表1中可看出，本文提出的密码方案在安全性、计算量和存储空间等方面具有一定的优势。

下面通过理论分析和仿真对本文提出方案的公钥和私钥大小和其他相关方案进行比较。在具体的量化仿真中，n是安全参数，q是模数，d＝「logn⏋，m＝6nlogq，¯m＝nk，l是消息的比特长度。 其中在文献[14]Micciancio方案和[19]Cash方案中，k＝「logn⏋；在文献[22]Ducas方案中，w1＝2「logq⏋＋2，k1＝2「log3q⏋。在Cash方案中的公钥与私钥大小分别为：2l¯mn＋2¯mn和4¯m2；在文献Micciancio方案中的公钥与私钥大小分别为：(l＋1)n2k＋(¯m＋nk＋1)n和¯mnk；在Ducas方案中的公钥与私钥大小分别为：(d＋3)n2k1＋n和w1k1n2；本文方案中的公钥与私钥大小分别为：2d¯mn＋4nk和¯mnd。当l＝100，q＝212时，不同方案中在不同安全系数下公钥大小的比较：

从图2可以看出，本文提出方案的公钥和私钥大小占有一定的优势。

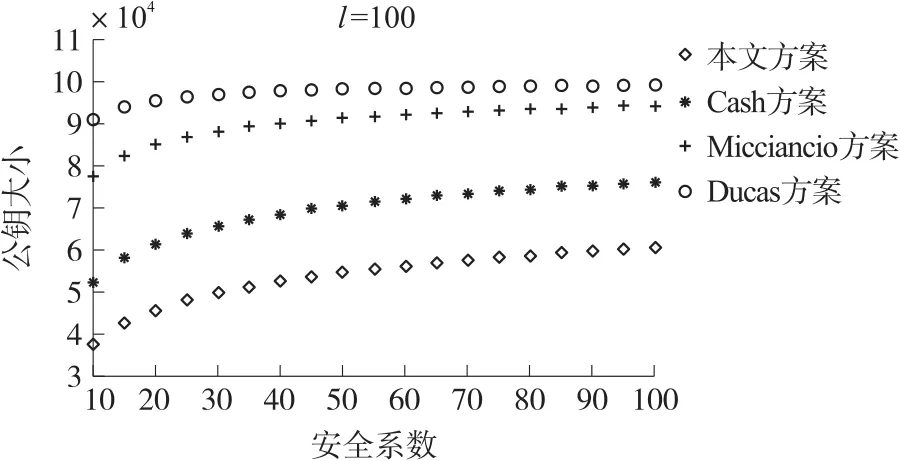
图2 本文方案与相关协议的公钥大小比较

本文提出的密钥协商协议不需要相关传感器节点再另外单独发送密钥数据包，因为包含密钥的信息已经被嵌入到密钥协商的数据包中，第j个传感器节点接收到密钥协商协议数据包就可以通过对密钥协商数据包的验证，并提取出相应的临时会话密钥信息。由于本文提出的密钥协商协议不需要额外发送消息，因而能够减少无线传感器网络的通信开销，达到降低能耗的目的。另外用于第i个传感器节点和第j个传感器节点进行临时通信的密钥是基于对称密码体制算法，所以能有效提高第i个传感器节点和第j个传感器节点临时通信的效率。在计算复杂性方面，本文提出的密钥协商协议主要操作都是些简单的哈希操作和逻辑运算，一般传输1比特的数据比32比特的计算要消耗更多的能量。

5 总结

本文提出了一种有效的无线传感器网络密钥协商协议，其核心思想是采用格上无需原像抽样操作的算法，利用格上坚实的安全基础和更高的计算效率，使其更适应于无线传感器网络。在本方案中，传感器节点不需预先存储会话密钥信息，只在需要通信时才发起密钥协商会话来建立配对密钥，而通信的密钥是基于对称密码体制算法，所以能有效降低传感器节点之间的通信开销。