一种低能耗的无线传感器网络强栅栏重建方法研究∗
陶建林,苗春雨,戴国勇
(1.浙江工业职业技术学院,浙江绍兴312000;2.浙江师范大学数理与信息工程学院,浙江金华321004;3.浙江工业大学计算机科学与技术学院,杭州310023;4.安恒信息技术有限公司网络空间安全学院,杭州310051)
无线传感器网络栅栏覆盖在入侵检测等诸多领域都有着广泛的用途,如可将传感器网络部署在工厂周围,有效的监测污染物的扩散范围;在军事方面,将传感器部署在阵地前沿,能够有效的监测敌人是否发动突袭[1-2]。无线传感器网络主要部署在带状区域或环形区域中,将区域一分为二,其作用是高效的监测目标是否由一个区域穿越到另一区域中,这种技术被称为无线传感器网络栅栏覆盖[3-4]。传感器网络由于节点自身原因或外界因素的影响(泥石流、洪灾等),栅栏极易被破坏,从而导致栅栏失去功能[5]。在栅栏被破坏后如何修复和重建是热点研究问题。
目前的研究一般采用移动节点解决栅栏间隙问题,如Saipulla等人[6]提出栅栏间隙的寻找方法,并利用最大流算法和二分法对栅栏间隙进行修复,使修复代价最小。戴光麟等人[7]改进了参考文献[6]提出的方法,利用邻居可移动节点集合降低了修复算法的复杂度。Xu B等人[8]建立入侵轨迹模型预测入侵者穿越栅栏时的位置,并将可移动节点移动到频繁穿越位置强化栅栏,防止出现栅栏间隙。Deng等人[9]研究了一种混合传感器网络栅栏间隙修复方法,假设传感器节点的感知范围可调,利用移动节点修复栅栏使得移动距离最短。Chen等人[10]根据节点间距离查找栅栏间隙,并通过旋转栅栏中关键传感器节点或一段栅栏修复栅栏间隙。Dash等人[11]提出一种分布式的栅栏修复方法,首先查找间隙处是否有冗余栅栏可以替换,如果有,则替换,否则派遣移动节点对间隙进行修复。Xu H等人[12]提出最小费用方案和自适应贪婪移动方案修复栅栏间隙,其中最小费用方案为集中式算法,修复栅栏间隙费用最小。上述栅栏间隙修复方法都是利用可移动节点修复栅栏较短的栅栏间隙,而不适用于栅栏被大段破坏后的重建问题。
在栅栏重建方面的研究,如Tian等人[13]根据不同天气,调度不同类型的传感器节点,实现雨天和晴天的栅栏重建。而针对栅栏出现大范围破坏后的重建研究较少,栅栏间隙修复和重建的区别在于失效栅栏的长度,栅栏间隙一般较短,使用少量可移动传感器节点即可完成修复,而重建栅栏的长度较长,需充分利用静态传感器节点以降低代价。本文利用KSP算法寻找k条重建路径,然后利用Hungarian算法选择最佳重建路径并派遣可移动节点重建栅栏,使能耗尽可能的降低。
1 相关模型和定义
1.1 相关模型
①传感器节点采用二元感知模型,以传感器节点为圆心,感知半径为r,当监测目标进入感知范围内,传感器节点能够监测到目标的概率为1,否则为0,如式(1)所示,静态传感器节点和可移动传感器节点的感知半径相同。

式(1)中o表示传感器节点,t表示监测目标,d(o,t)表示传感器节点与监测目标的欧氏距离,Po,t表示节点监测到目标的概率。
②可移动节点在移动时消耗的能量远远高于感知消耗的能量,因此可移动节点感知消耗的能量忽略不计,且移动过程消耗的能量与移动距离呈正比,移动1 m消耗的能量为3.6 J[14-15]。
1.2 相关定义
定义1 栅栏重建,当栅栏遭受大范围的破坏后,利用静态节点和可移动节点重新构建栅栏的过程,如图1中一段较长的栅栏受泥石流冲击后,传感器节点脱离了栅栏,需对损坏的栅栏段进行重建。
定义2 重建路径,充分利用静态传感器节点重建栅栏,从栅栏损坏段的最左端S节点开始,经过若干个静态传感器节点到最右端D节点,则经过的路径被称重建路径,其中重建栅栏消耗能量最少的路径称为最佳重建路径。
定义3 修复位置,如图1,重建路径中节点i和j的感知区域并没有重叠,如果可移动节点移动到位置m,使得节点i和j之间的边被感知区域完全覆盖,则称m为修复位,如果需要多个可移动节点才能完全覆盖节点之间的边,则修复位在节点之间的边上均匀分布。
定义4 栅栏重建能耗,指可移动节点完成栅栏重建所消耗的能量总和,因此只与移动节点的总移动距离有关。
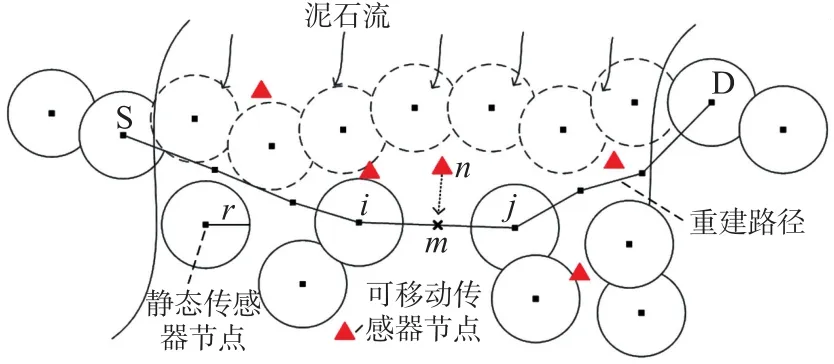
图1 栅栏重建图
2 栅栏重建路径
2.1 全连接拓扑图建立
假设传感器节点已利用GPS设备或相关定位算法获得了自身的位置,为充分利用静态传感器节点,减少可移动节点的使用,首先利用部署区域中的静态传感器节点构建全连接拓扑图G(V,E),如图2所示。假设栅栏重建处有4个静态传感器节点n1、n2、ni、nj,以左侧栅栏最右端节点 S 为开始点,右侧栅栏最左端节点D为结束点构建全连接拓扑图,其中 V 和 E 如式(2)、式(4)所示,numi,j表示节点 ni和nj之间的边被节点感知范围完全覆盖所需最少传感器节点的数量,如公式(5)所示。

图2 静态节点全连接拓扑图

式(2)表示拓扑图G中静态传感器节点集合,nw表示静态传感器节点,w表示G中静态传感器节点数量,式(3)中 ei,j表示节点 ni和 nj之间的边(节点S和D对应的边也包含其中),式(4)表示拓扑图G的边集合,sn为图G节点总共数量,sn=w+2,式(5)中d(ei,j)表示静态节点ni和 nj之间的欧氏距离,r表示节点的感知范围,1≤i,j≤sn。
2.2 栅栏重建路径选择
影响栅栏重建能耗的因素有2点:①需要移动的传感器节点数量;②可移动节点在重建栅栏时的移动平均距离。由于本文假设传感器节点在区域中均匀随机部署,因此暂时无法选择某条重建路径使重建栅栏的能耗最低(节点的移动距离总和最短),但可以从所需移动节点数量上考虑,当某条重建路径所需的可移动节点数量越少,则重建栅栏所消耗的能量越小的概率越高,因此本文利用KSP算法[16-18]搜索拓扑图G中所需移动节点数量由少到多的前k条重建路径,表示为集合Rp,如式(6)所示,当k取值合适时,最佳修复路径被包含在这k条路径中,倘若寻找到最佳重建路径,则可达到栅栏重建能耗最低的目的。


图3 重建路径修复图
3 移动节点重建栅栏过程
3.1 重建路径判断
在1.2小节利用KSP算法寻找到k条重建路径,但并非都能够完成栅栏的重建。由于可移动节点数量和移动距离有限,最大可移动距离为R,当重建路径上的修复位置不能被移动节点完全覆盖,则该重建路径不能完成栅栏重建,如图3所示。
重建路径path1存在3个修复位置,在移动范围R内,可移动节点mn1移动到修复位置2,mn2移动到修复位置3,完成这两个修复位置的修复,但是没有移动节点可移动到修复位置1,因此重建路径path1没有足够的移动节点完成栅栏重建。
参考文献[6]提出利用最大流方法判断栅栏间隙能否被修复,但该方法相对复杂,不适用于栅栏重建问题。本文提出一种基于集合运算方法判断某条重建路径能否成功重建栅栏,如图4所示。

图4 栅栏重建判断图
图中栅栏重建路径从S点开始,到D点结束,存在3个修复位置,倘若所有的修复位置至少都能够分配到一个可移动节点,则沿着该重建路径能够重建栅栏。在移动距离为R时,可移动到修复位置1、2、3的移动节点集合分别表示为 Set1={mn1,mn2}、Set2={mn2}、Set3={mn3,mn4,mn5},当同时满足以下三个条件时,该路径能够完成栅栏的重建。
①所有移动节点集合并集的元素数量大于或等于重建路径中修复位置总数,即|Set1∪Set2∪……Sett|≥t,t为重建路径中修复位置的总数。
②所有移动节点集合都不为空,即对a取任何值,Seta≠∅,1≤a≤t。
③任意两个修复位置的移动节点集合并集的元素数量都大于或等于2,即对a,b取任何值,都满足|Seta∪Setb|≥ 2,1≤a,b≤t,a≠b。
基于上述三个条件,可以判断图4所示的重建路径能够完成栅栏的重建。具体判断方法如表1所示。

表1 重建路径能否重建栅栏的判断方法表
3.2 最佳栅栏重建
2.2小节采用KSP算法选择了k条重建路径,然后利用3.1小节提出的重建路径判断方法筛选出若干条(H条)能够完成栅栏重建的重建路径,本节采用改进的Hungarian算法派遣可移动节点重建栅栏,并从H条重建路径中找到一条最佳重建路径,使移动节点消耗的能量总和最少。
Hungarian算法一般用于人员最优指派问题,假设u个工人去完成u个任务,每个任务只能派遣1个工人,而每个工人对不同任务的熟练程度是不同的,Hungarian算法能够最优的指派人员去做相应的工作,使完成所有工作花费的时间总和最短[19-20]。因此该算法能够贴切的应用于栅栏重建时的可移动节点派遣问题,使所有节点的移动距离总和最少。在H条重建路径中的任意一条都满足修复位置总数(z)少于等于可移动节点总数(t),即满足3.1小节的条件1。将可移动节点派遣到修复位置问题类比到人员指派问题,用t个可移动节点移动到z个修复位置,每个修复位置最多接受一个可移动节点,则剩余t-z个可移动节点没有使用,因此本文在修复路径上虚拟出t-z个虚拟修复位置,使t个可移动节点被派遣到t个修复位置,具体方法如图5所示,总共分为两种情况。
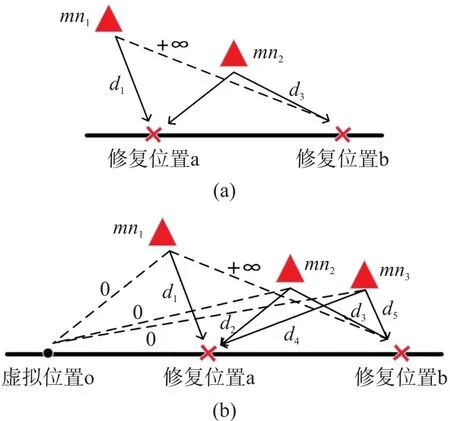
图5 移动节点与修复位置情况图
图5 (a)重建路径中存在2个修复位置,且可移动节点数量也为2,可移动节点mn1可以移动到修复位置a,距离为d1,而不能移动到修复位置b(超出可移动节点的最大可移动距离R),则规定mn1移动到修复位置b的距离为+∞;节点mn2可同时移动到修复位置a和b,距离分别是d2和d3,利用节点与修复位置的距离作为重建栅栏的代价,构建Hungarian算法的代价矩阵,如式(7)所示。

图5(b)重建路径中存在2个修复位置,而可移动节点有3个,因此需要虚拟一个修复位置,如图5(b)中虚拟位置o所示。所有可移动节点与虚拟位置o的距离都为0,假设可移动节点与修复位置的距离大于移动节点的最大移动距离R时,则规定该节点与修复位置的距离为+∞。构建的Hungarian算法代价矩阵如公式(8)所示。
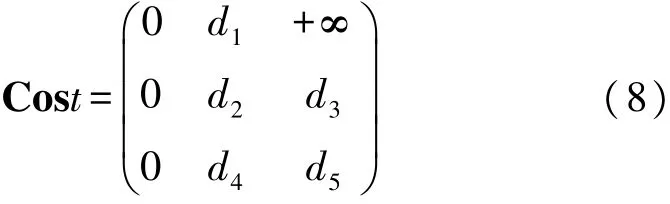
在重建栅栏过程中,根据上述两种情况构建重建路径的代价矩阵,然后利用Hungarian算法分别计算H条重建路径的重建代价,即沿每条重建路径重建栅栏,移动节点的移动距离总和,最后选择节点移动距离总和最短的一条重建路径,该路径为最佳重建路径,并派遣移动节点沿最佳重建路径重建栅栏使得总能耗尽可能降低,实现算法如表2。

表2 最佳栅栏重建表
4 仿真实验
采用 i5处理器、8 G内存的 PC机,利用MATLAB平台进行仿真实验。将静态和可移动传感器节点按照不同比例随机均匀的部署在一个长为3 000 m,宽为300 m的矩形区域中,节点总数为100,所有节点感知半径r相同,可移动节点的最大移动距离为R。该区域中存在一条被破坏的栅栏,对损坏部分进行重建(节点S和D之间),如图6所示。实验从栅栏重建的移动节点需求数量、可移动节点的平均移动距离、栅栏重建总能耗和栅栏重建率四项指标分析对比了BRMLE栅栏重建方法和参考文献[6]提出的最佳栅栏修复方法Optimal(栅栏修复是栅栏重建的一种)。
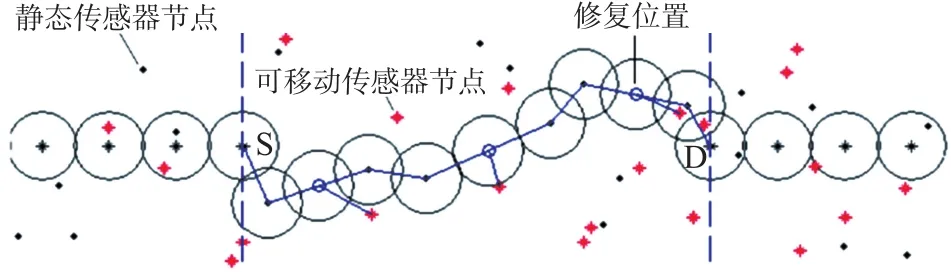
图6 栅栏重建结果图
4.1 栅栏重建长度影响
栅栏重建长度是影响重建的重要因素之一,理论上重建长度越长,则需要的可移动节点数量越多,消耗的能量越多,栅栏重建率越低。实验中可移动节点的最大移动距离R=70 m,同时实验分析了可移动节点占40%和60%的情况对栅栏重建的影响,结果如图7所示。
图7(a)分析了栅栏重建长度与可移动节点需求数量的关系,实验结果表明Optimal方法在可移动节点比例为40%和60%时,重建栅栏所需要的可移动节点数量相同。随着重建长度的增加,完成栅栏重建需要的可移动节点数量呈线性增加,在重建相同长度的栅栏时BRMLE方法需要的可移动节点数量少于Optimal方法(当可移动节点比例为40%时,重建2 700 m的栅栏,Optimal方法平均需要31个可移动节点,而BRMLE方法仅需要18个可移动节点),因为BRMLE方法充分利用静态传感器节点,当静态传感器节点不能完成栅栏重建时,才派遣可移动节点,而Optimal方法完全采用可移动传感器节点完成栅栏重建。BRMLE方法中可移动节点占比越低,需要的移动节点数量越少,有利于节约成本。
图7(b)分析了栅栏重建长度和可移动节点平均移动距离的关系,实验结果表明栅栏重建长度与可移动节点的平均移动距离无关,栅栏重建过程中,可移动节点的平均移动距离基本保持稳定,在可移动节点占比相同的情况下BRMLE方法和Optimal方法的可移动节点平均移动距离基本相同,因为可移动节点在部署区域中均匀随机分布。可移动节点占60%时平均移动距离为24.3 m,可移动节点占40%时平均移动距离为31.5 m,因为可移动节点占比越高,移动节点在区域中越密集,到达修复位置的距离越短。
图7(c)分析了栅栏重建长度与栅栏重建总能耗的关系,能耗模型如1.1小节所示,重建能耗和可移动节点需求数量、节点的平均移动距离相关,实验结果表明随着栅栏重建长度的增加,总能耗呈线性增加,因为栅栏重建长度增加,需要的可移动节点数量呈线性增加,而在可移动节点比例不变的情况下,平均移动距离基本稳定,因此总能耗呈线性增加。BRMLE方法消耗的总能量低于Optimal方法,当可移动节点占40%时,重建2 700 m栅栏,BRMLE方法消耗的能量为75.3 J,Optimal方法消耗的能量为1498.6 J,因为BRMLE方法充分利用静态传感器节点,需要的可移动节点数量少于Optimal方法,而两种方法的可移动节点平均移动距离基本相同,导致BRMLE方法重建栅栏时可移动节点的总移动距离更短,因此消耗的总能量越少。
图7(d)分析了栅栏重建长度和栅栏重建率的关系,实验结果表明随着栅栏重建长度的增加,栅栏重建率逐渐降低,其中BRMLE方法降低的幅度逐渐减少,最终区域平稳,而Optimal方法的栅栏重建率呈线性降低。栅栏重建长度相同时,BRMLE方法的栅栏重建率远远高于Optimal方法,当可移动节点占40%时,重建2 700 m栅栏,BRMLE方法的重建率为64.7%,而Optimal方法的重建率为11.4%。

图7 栅栏重建长度分析结果图
4.2 节点比例影响
实验分析可移动节点占总节点比例对栅栏重建的影响,实验中重建1 000 m的栅栏,同时分析了可移动节点不同最大移动距离R情况下算法的性能。
图8(a)分析了可移动节点比例和可移动节点需求数量关系,实验结果表明随着可移动节点比例的增加,BRMLE方法需要的可移动节点数量逐渐增加,而Optimal方法不变,因为Optimal方法直接重建S到D的直线路径,因此需要的移动节点数量不变,而BRMLE方法需要利用静态传感器节点,当可移动节点比例增加,静态节点的比例降低,因此需要的可移动节点数量增加。BRMLE方法需要的可移动节点数量低于Optimal方法,当可移动节点占100%时,两种方法需要的可移动节点数量相同,因为此时BRMLE方法的栅栏重建路径与Optimal方法相同。
图8(b)分析了可移动节点比例与节点平均移动距离关系,实验结果表明随着可移动节点比例的增加,平均移动距离都逐渐减低,最后区域平稳,因为可移动节点的比例增加,则部署区域中可移动节点密度越大,距离重建路径中修复位置的距离也就越近。且在R相同时,BRMLE和Optimal方法的平均移动距离基本相同。
图8(c)分析了可移动节点比例与栅栏重建总能耗关系,实验结果表明随着可移动节点比例的增加,BRMLE方法消耗的总能量逐渐增加,因为可移动节点比例增加,静态节点的比例降低,需要的可移动节点数量会增加,而节点平均移动距离降低,综合来看,消耗的总能量小幅度升高。Optimal方法消耗的总能量逐渐降低,因为可移动节点比例增加,Optimal方法需要的可移动节点数量不变,而可移动节点的平均移动距离降低,因此消耗的总能量降低。BRMLE方法消耗的总能量低于Optimal方法。
图8(d)分析了可移动节点比例与栅栏重建率关系,实验结果表明随着可移动节点比例增加,栅栏重建率都成升高趋势。在可移动节点比例相同时BRMLE方法的栅栏重建率远高于Optimal方法,因为BRMLE方法选择需要可移动节点数量最少,移动距离总和最短的重建路径,因此具有较大的概率完成栅栏的重建。
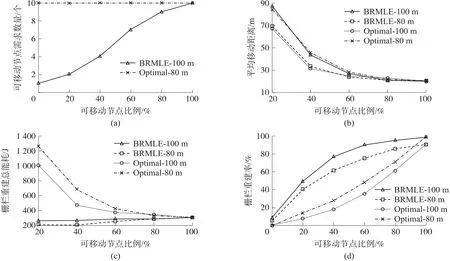
图8 节点比例分析结果图
5 总结
研究了一种能耗优先考虑的1-强栅栏重建方法(BRMLE),利用KSP算法搜寻k条重建路径,然后利用Hungarian算法选择最佳重建路径并派遣可移动节点完成栅栏的重建。实验与目前较优秀的Optimal方法进行对比,证明了BRMLE在可移动节点需求数量、栅栏重建率、能量消耗等方面都具有较好的性能。后续工作希望进一步研究K-强栅栏重建方法。

