让学生享受明白易懂的智趣数学

○吴汝萍

数学知识最基本的特征是抽象，它舍弃了事物的其他方面而仅仅保留数量关系和空间形式。小学生思维最基本的特征是形象，处于从具体形象思维慢慢过渡到抽象逻辑思维的阶段。数学课堂上，经常会有这样的画面：教师喋喋不休讲解，学生静静坐着，眼睛虽盯着教师，可眼神一片茫然。因为学生听不懂，思维已跟不上教师的节奏。学生不喜欢数学往往是从听不懂、学不会开始的，进而会导致惧怕数学，甚至患上数学恐惧症。教师要想让学生愿意跟着自己一起学数学、玩数学，就必须让学生学习能够看得见的、摸得着的、说得清的、理得顺的、悟得透的数学，让学生享受明白易懂的数学。

一、深入浅出，有效迁移

数学教师是否能深得学生的青睐，不在于教师是否有满腹经纶的数学知识，也不在于教师是否能熟练解答出一道道高难度的数学问题，关键在于教师的数学教学能否深入浅出，让学生感到数学是明白易懂的，是好玩有意思的。深入浅出的数学课堂是学生期盼的，也应该是教师数学课堂教学追求的常态。

1.深入——高观点立意。

“深入”是教师理解教学内容时要站得高、看得远，即站在更高更广的知识体系中去理解和把握数学知识的本质。居高才能临下，高屋方可建瓴。教师教学水平的高低，首当其冲是体现在对教学内容的把握上。教师备课时要高观点立意，深入研究教材，对知识体系进行宏观审视，不仅要关注相关知识的前后联系，帮助学生有效构建知识结构，还要抓住数学知识的本质，看清知识背后所蕴含的数学思想方法，注重数学思想方法的渗透和数学思维能力的培养。

2.浅出——低起点切入。

“浅出”是教师要基于学生的已有认知起点和已有的生活经验组织教学。低起点切入，是让每天所教的数学知识都有所植根，是从学生已有的知识中生长出来的，让学生知道它的“前世”“今生”，使学生能够积极地参与到学习的过程中。教学过程中，教师的讲述和提问也必须浅显易懂，并能启人深思、耐人寻味，让学生“跳一跳能摘到果子”。这样，就可以让学生对每天所学的新知识都能理得顺、说得清，并在头脑中形成较为合理的数学认知结构。

3.迁移——高目标达成。

高观点“深入”，低起点“浅出”，其目的是促进知识的有效迁移，在不知不觉中，学生的数学认知能力会到达一个新的高度。

如二年级“认识一千以内的数”，让学生一个一个数，数类似“309后面一个数”时，很容易出错，误认为309的后面是400。教师可以先让学生回忆100以内数的顺序，说一说9、19、29、39等这些数的后一个数。然后引导学生根据9的后面是10，推想出109后面的一个数是110。并用计数器验证推想的结果，学生清楚地看到9的后面是10，109的后面是110。接着再让学生根据109的后面是110，推想“1□9”的后一个数。学生很快就推想出119的后面是120，129的后面是130等等。最后再让学生根据199的后面是200，推想出“□99”的后一个数。

如此教学，学生会将百以内数的数数方法有效迁移运用到数千以内的数，学生对千以内数的顺序的认知一下子就变得清晰通透了，认知能力也得到了极大的提升。

二、少谕多喻，触类旁通

“谕”是明确告诉，直言使人知道。“喻”是相机诱导，不明言而暗示之。教师要少谕多喻，因为让学生理解抽象的数学知识，靠教师在抽象层面反反复复讲解几乎是没有实效的。教师唯有善“喻”，举例子或打比方，才能启发、诱导学生实现认识上的飞跃。

1.善举例子，让数学概念明白易懂。

一个正方形的边长是4厘米，学生会误认为它的周长和面积相等。如果教师只是反复强调，周长和面积是两个不同的概念，不好比较，但学生并不能真正理解。此时教师不妨举个例子：小红身高12分米，小明体重12千克，能否说“小红身高和小明体重一样”，也就是“12分米和12千克相等”？如果不相等，能否说“12分米大于12千克”或者说“12分米小于12千克”？

因为身高和体重是学生非常熟悉的两个不同的概念，12分米是身高，12千克是体重，自然不能放在一起比较。由此，学生就容易触类旁通，认识到周长度量的是封闭图形一周的长度，面积度量的是封闭图形围成的面大小，是完全不同的概念，从而理解周长和面积不能比较大小。

2.善打比方，让数学算理明白易懂。

计算末尾有0的乘法，学生简算时很容易出错。一方面是学生对运用积的变化规律进行简算的算理没有真正理解，另一方面对“去0”“添0”的简算方法掌握不到位。如：

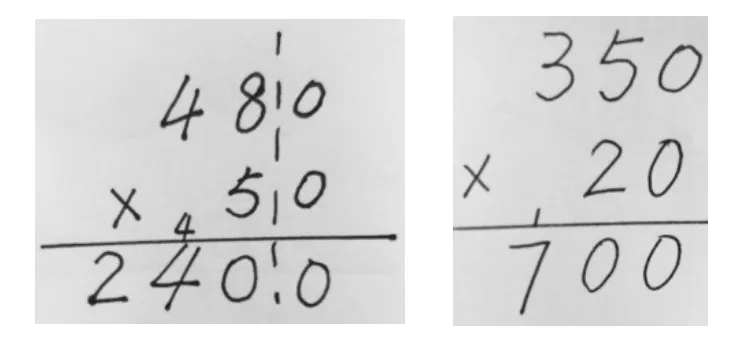
教学过程中，不妨给学生打个比方：学校召开春季开运动会，天气比较阴冷，大家都穿着厚厚的长衣长裤。运动员上场比赛时，为了便于奔跑，会脱掉厚厚的长衣长裤（相当于“去0”），只穿短衫和短裤上场参赛。比赛结束，要及时穿上长衣长裤（相当于“添0”），否则就会受风寒，造成身体上的不适。

然后结合末尾有0的乘法简算进行理解：先去掉0，用0前面的数相乘，是为了方便计算，相当于前面的“脱衣服”，乘之后需要添上刚刚省去的0，相当于前面的“穿衣服”，脱了几件，就要穿上几件，忘记添0或少添了0，结果都会导致“问题”发生。

三、数形结合，形象直观

“数形结合”其实质是将抽象的数学语言与直观的图形结合起来。“一图抵百语”，以“形”的直观表达“数”，用“数”的精确研究“形”。由“数”观“形”，借“形”思“数”，使抽象的数学问题变得形象直观、简洁明了。

1.数形结合，让数学概念明白易懂。

以形象思维为主的小学生要深刻理解抽象的数学概念，自然是有一定的难度。要让学生真正理解相关数学概念，简单有效的方法就是“数形结合”。

如“小数的意义”，如果只让学生反复读记“一位小数表示十分之几、两位小数表示百分之几、三位小数表示千分之几……”，是不能真正理解小数的意义并形成相关数感的。教师可以多让学生用不同的图形或物体来表征0.3、0.12、0.125等小数，看得见，摸得着，学生自然会觉得明白易懂。

2.数形结合，让计算算理明白易懂。

计算教学的相关内容看似简单，但如果学生没有真正理解算理，很难正确地计算。比如运用乘法分配律进行计算，学生很容易出错。

教学时，可以让学生先用图形来表示（4+5）×3，比如圆圈图。

接着让学生分开算出两部分的和，即4×3+5×3，进而借助图形来理解（4+5）×3和4×3+5×3之间相等的关系：（4+5）×3表示的是9个3，4×3+5×3表示的也是9个3。数与形的有机结合，使学生对算理的理解从纯粹的形式记忆中跳了出来，变得有“形”可依，有“理”有据，不仅能知其然，更能知其所以然。

3.数形结合，让数量关系明白易懂。

几年前，六年级期末测试卷上有这样一道填空题：一张长方形纸，长36厘米，从中剪下一个最大的正方形后剩下一个小的长方形，这个小长方形的周长是（ ）厘米。当时一位教师看到试卷后立即打电话给数学教研员，好心提醒此题缺少条件。

连教师都看不出此题的数量关系，可见题目中的数量关系隐藏之深。但是，只要画出图，隐蔽的数量关系自然清晰地呈现出来，无所遁形。如图，可以从图中清楚地看到：剩下的小长方形的长与宽的和就是原来长方形的长，所以剩下的这个小长方形的周长是原来长方形长的2倍，是72厘米。

4.数形结合，让数学问题明白易懂。

如一年级认识100以内的数后，让学生回答这样一个问题：“21个小朋友排成一队，按“1、2、1、2…”的顺序依次报数，结果是报单数的人多，还是报双数的人多？”全班异口同声：“报单数的人多！”接着教师追问：“如果是20个小朋友排成一队，按‘1、2、1、2…’的顺序依次报数，结果是报单数的人多，还是报双数的人多？”学生再次异口同声：“报双数的人多！”由此可见，学生只是根据“21是单数、20是双数”判断得出结论的，实际上根本不明白数学问题到底与什么有关。如果教师只是用言语表述：“你们说错了，20人排成一队时，报单数和双数的人一样多。”学生一定是一头雾水，根本弄不清楚其中的原因。

此时，不妨让学生自己在纸上画一画：画20个圆圈，表示20个小朋友，并在圆圈上依次写上“1”和“2”。等学生写完，自然能看清楚结果和自己想的完全不同：报“单数”和“双数”的人一样多。最后再让学生讨论：什么情况下报“单数”的人多？什么情况下报“单数”和“双数”的人一样多？为什么不存在报“双数”的人多？因为学生自己所画的直观示意图清楚地呈现在眼前，讨论的过程中，学生说得清，道得明，悟得透。

总之，教师需要使出浑身解数，来增强数学的直观性，更要努力当好“红娘”的角色，让数学课堂成为学生和数学“约会”的最佳场所。在学生与数学一次次接触的过程中，让他们体验到数学不难，明白易懂，数学有用，能解决很多问题。如此，学生就会有“入乎其内”兴趣，其心智也就会乐意走进数学的大花园中来，欣赏到美丽的风景。