提高星载GPS接收机RAIM算法运行效率的方法研究
隋叶叶,刘恒毅,万程程,马文聪,刘杰强
(航天恒星科技有限公司,北京 100086)
随着星载GPS接收机在航天领域的广泛应用,航天器对接收机的可靠性和可用性提出越来越高的要求。星载GPS接收机除了要提供定位、导航和授时功能外,还必须具有在系统不能使用时及时向用户发出警告的能力,这种能力称为系统的完好性。RAIM(接收机自主完好性监测)是一种仅依靠接收机自身获取的定位观测量进行监控的方法。它无需外部设备辅助,花费较低,容易实现,是目前应用较为广泛的一种完好性监测算法[1-2]。
RAIM技术国内外研究较多,最小二乘残差方法(SSE)和奇偶空间方法(Parity)是目前应用最为广泛的两种方法,但是其应用也仅限于航空和地面[3]。国外目前在航天领域的应用还没有文献涉及,国内也没有相关文献。而对于资源十分有限、运行时间要求严格的星载GPS接收机而言,需进一步提高RAIM算法的运算效率。
本文在对两种方法实现原理进行研究的基础上,对两种方法按故障检测统计量构造、可用性判断、故障检测、故障识别等4个模块分别进行运算量的比较,得出两种方法各自的优劣势,提出一种提高RAIM运算效率的方法,即基于最小二乘方法构造检测统计量的奇偶空间改进方法,并利用工程样机,对改进方法进行实际验证,证明该方法的有效性。
1 RAIM算法原理
观测误差可以通过故障检测统计量反映出来,利用数理统计的假设检验方面的内容对检测统计量进行分析可以检验系统中是否存在粗差(没有模型化的偏差)。根据此原理,RAIM的判定流程图如图1所示。
图中PPL为定位保护限(在当前几何分布条件下满足漏检概率要求的最大可能误差),PAL为定位告警限(最大允许定位误差),n为可见星数目,H为观测矩阵,TD为告警门限值,T为检测统计量。
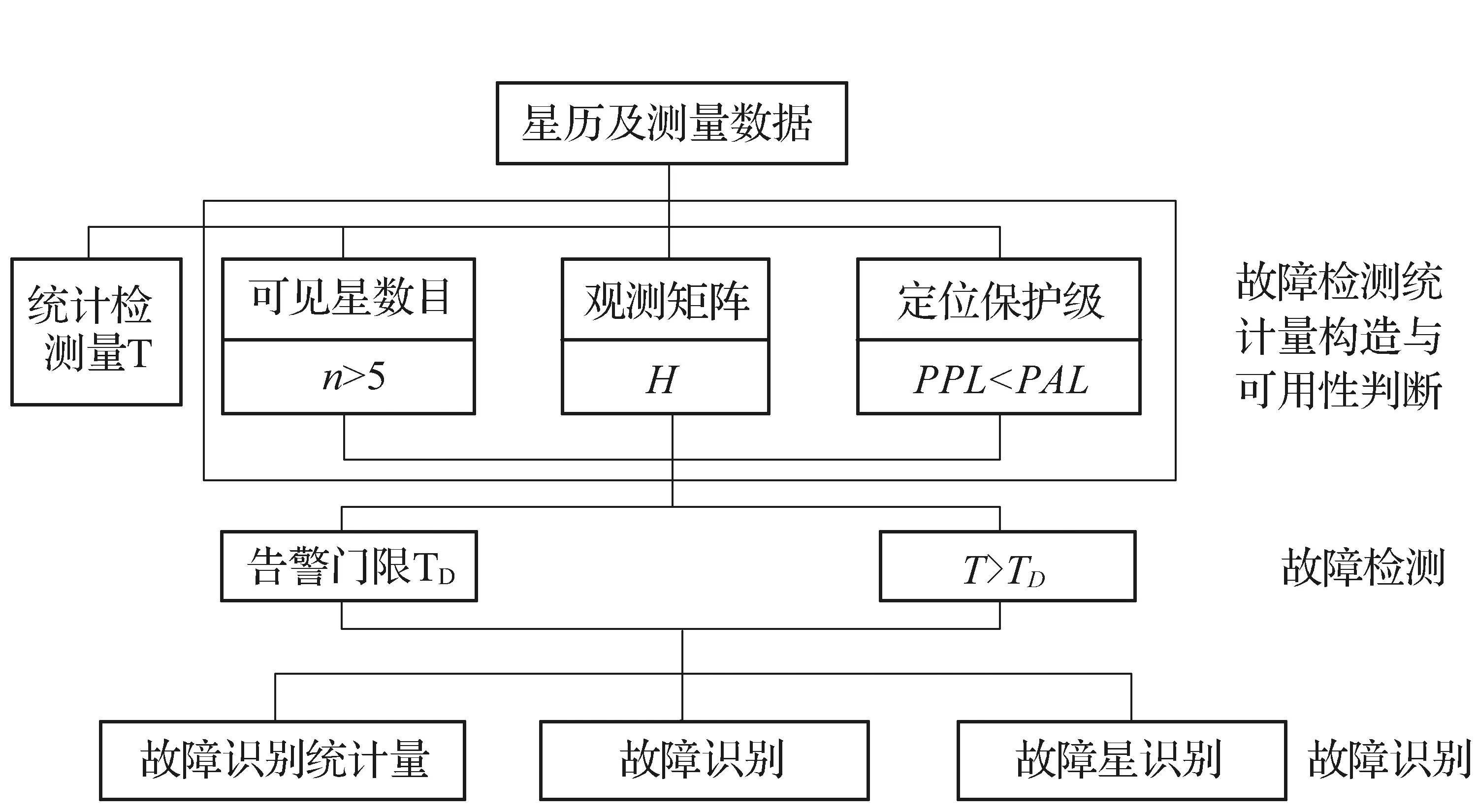
图1 RAIM判定流程图
由于在卫星几何条件不佳时,某颗较差的卫星尽管产生较大的定位误差,但单位权中误差却很小,可能会导致漏检。因此,为保证漏检概率尽可能小,必须在卫星的几何分布满足一定条件时,才能应用RAIM算法,否则就不能用RAIM来进行故障星检测。将反映卫星几何分布的PPL值与PAL比较,在PPL不超过PAL时,判定算法可用。同时,解算的星历与测量数据作为输入构造检测统计量。检测门限为根据统计量所服从的统计分布,在满足系统所要求的误报概率的条件下,通过一定的变换关系确定。统计量超过检测门限说明有故障星的存在,进行故障星的识别。
最小二乘残差方法与奇偶空间方法均是基于此判定流程进行接收机自主完好性监测的,区别在于它们分别基于距离、奇偶两个不同的空间进行。
1.1 基于最小二乘残差的RAIM算法
n个伪距观测值的误差模型可以表示为[4]
y=Hx+ε.
(1)
式中:y为伪距残余,代表实际测量伪距与预测伪距的差值;H为由状态空间向测量空间的转移矩阵;x为用户实际位置的3个分量的增量偏移和接收机时钟偏差;ε表示观测伪距噪声矢量。
伪距残余可表示:

定义伪距残余各分量的平方和为SSE=wTw.通常,取检测统计量[5]:
(2)
检测门限TD的确定与所要求的误报概率PFA有关:
TD=σ02Q-1(PFA|(n-4)).
(3)
其中,Q-1(P|r)是Q(x2|r)的逆函数。将检测统计量T与检测门限TD比较,若T 给定漏检概率PMD,应满足如下概率等式[6-7] (4) 由上式可得非中心化参数。由空间位置定位误差警报阈值PAL(Positioning Alert Limit,由系统需求给出或用户自己定义)可得到精度因子变化的限值: (5) 故障检测前,实时计算每颗可见星的δPDOP值,并取最大值为δPDOPmax,若δPDOPmax<δPDOPT,表示该时刻RAIM可用。 对系数矩阵H进行QR分解,并将QT和R分别表示为Q=[QxQp]T,R=[Rx0]T,其中,Qx为QT的前4行,Qp为剩下的n-4行,Rx为R的前4行。 奇偶空间矢量表示为[3] p=Qpy=Qp(Hx+ε)=Qpε. (6) 故障检测统计量为 式中:Qp为奇偶空间矩阵。为最大化偏差的可视性,将奇偶矢量投影到Qp的每一列,并进行标准化,可得到故障识别统计量: (7) 给定误报概率PFA,可以得到检测限值: Tr=Φ-1(1-PFA/2n). (8) 对每个统计量ri与Tr比较,若ri>Tr,则检测到该卫星有故障。 给定漏检概率PMD,满足PMD条件下的最小检测偏差: bi=(Tr+erf-1(PMD))/|Qpi|. 偏差bi产生的定位误差[8]: (9) 取最大定位误差,则空间位置定位误差保护级别为 (10) 此PPL值表示满足PMD条件时可能达到的最大定位误差,若其小于定位误差告警限值PAL,则故障检测具有完好性保证(即RAIM可用)。 若以奇偶矢量的平方和作为校验统计量,有 (11) 也就是 Qpy=Qpw=p, pTp=(Qpy)T(Qpy)=(Qpw)T(Qpw)= wTQpTQpw=wTw. (12) 在观测值满足正态分布,误报漏检率相同的情况下,在距离空间和奇偶空间的残差的平方之和是相同的,即Parity方法和SSE方法在检测性能上是等效的。 RAIM算法包括故障检测统计量的构造、可用性判断、故障检测、故障识别4个软件模块。结合两种方法的实现原理,对它们分别从4个模块进行运算量差异的比较。 表1看出,由于涉及到运算复杂QR分解,Parity方法的检测统计量构造模块的运算量相比SSE方法检测统计量构造模块运算量大很多;而在奇偶空间进行可用性判断、故障检测与故障识别运算量更小。因此,为了进一步减小RAIM的运算量,进行算法的优化,本文结合每种方法各自优势,设计出一种适用于空间飞行器的改进方法。 表1 SSE与Parity方法运算量差异比较 注:0代表运算量无差异。其中,n为可见星数,m为检测统计量构造过程中的迭代次数 基于以上两种RAIM方法的分析与比较,可以得出,两种方法在故障检测与识别效果上是等价的,但是由于两者运算角度的差别,即分别基于距离空间和奇偶空间的运算,两者运算量差异较大。 由于空间飞行器上接收机的处理器资源有限,且对算法的执行效率有严格的要求,寻求算法的优化至关重要。基于星载GPS接收机的RAIM算法需要针对特殊的应用环境寻求提高运算效率的方法。 两种RAIM方法构造两个不同空间的检测统计量,其中最小二乘残差方法选择伪距残余构造故障检测统计量,奇偶空间方法选择奇偶空间矢量构造故障检测统计量。本文结合两种不同RAIM方法的优势,通过一次观测阵的QR分解,基于最小二乘方法构造奇偶空间的检测统计量,并在奇偶空间进行可用性判断、故障检测、故障识别,通过该方法,达到运算量简化的目的。改进方法示意图如图2所示。 图2 改进方法示意图 如图2所示,将最小二乘收敛后的观测矩阵进行一次QR分解,利用产生的Q及R矩阵构造奇偶域故障检测统计量,并在奇偶空间进行可用性判断、故障检测与故障星识别。 在最小二乘准则下,可得到未知参数的最小二乘估计: (13) 在最小二乘迭代收敛后,对观测矩阵进行QR分解: H=QR. (14) 其中,QT和R分别分解: (15) 通过QR分解所得到Q阵构造故障检测统计量: p=Qpy. (16) 相应地,故障识别统计量构造: (17) 第i颗星上最小可检测偏差引起的定位误差为[8] (18) 则空间位置定位误差保护级别为 (19) 此PPL值表示满足PMD条件时可能达到的最大定位误差,若其小于定位误差告警限值PAL,则故障检测具有完好性保证。 该种方法基于最小二乘方法构造检测统计量,既能够发挥奇偶空间可用性判断、故障检测、故障识别运算量更小的优势,又能成功避免在奇偶域进行统计量求解的复杂运算。因此,相比最小二乘残差方法和奇偶空间方法,这种改进方法是一种提高运算效率的最优方案。 本文对该RAIM改进方法进行DSP实现,并将改进后的RAIM算法嵌入到接收机内部,进行算法的验证。为验证RAIM在轨工作性能,地面与仿真信号源联合进行测试,仿真时长为10 h。仿真信号源采用Sprint公司的SimGEN仿真控制软件,模拟产生星载GPS接收机射频信号,接收机接收信号进行电文的解算并得到定位结果,同时以1 Hz的频率通过同步串口向PC机发送解算数据,并在自编的自检界面将结果显示出来,供分析使用。以仿真轨道理论值为基准,对单点定位结果进行精度评估。 仿真中,初始开普勒轨道瞬时根数设置如表2所示。 表2 Simgen初始轨道设置 为了对该改进奇偶空间方法提高算法运算效率的效果进行验证,对最小二乘残差方法、奇偶空间方法及改进的奇偶空间方法3种方法的最大运行时间进行了统计。3种方法的平均运行时间及在满负荷运算(导航星数目为12颗)时不同算法的最大运行时间如表3所示。 表3 不同方法运行时间比较 ms 通过上表看出,3种方法中,改进奇偶空间方法的平均运行时间为12.67 ms,相比奇偶空间方法,运行时间缩短了4.68 ms,运行效率提高了27%。 在满负荷运行的情况下(即可用星达到12颗时),改进奇偶空间方法的最大运行时间为24.8 ms,相比奇偶空间方法,运行时间缩短了10.09 ms,运行效率提高了28.9%。 综合以上分析可以看出,3种方法中,无论从最大占用时间或随卫星数目而变化的统计时间考虑,改进奇偶空间RAIM算法占用时间均最少,更加适合星载接收机的使用。 在对改进奇偶空间方法的运算效率进行统计之后,验证该改进算法的效果,仿真信号源仿真在轨航天器数据,随机选择一颗卫星加入不同大小的伪距偏差,分别观察在不同工况下使用RAIM前后对定位结果的影响。 为了充分测试改进后RAIM的性能,设置如下三组工况: 工况1:伪距添加50 m误差; 工况2:伪距添加30 m误差; 工况3:伪距添加20 m误差。 每个工况分别按照“关闭RAIM模块”与“使用RAIM进行故障检测”两种情况进行验证,分别测试不同情况下的定位精度和检测性能。 在相同的轨道条件下,以理论轨道值作为轨道基准,对3组工况下的定位精度分别进行了测试。表4和表5分别列出了3种工况下做两种不同处理时的位置、速度精度。 表4 不同工况下做不同处理时的位置精度统计 m 表5 不同工况下做不同处理时的速度精度统计 m/s 从表格5中可以看出,在添加50 m误差时,三轴合成位置误差超过33 m,而使用RAIM进行故障检测后,该精度值降到7 m,定位精度得到明显改善。添加30 m及20 m误差时,三轴及单轴的定位精度也均有较明显的改善。从而证明该RAIM改进奇偶空间方法对于改善定位精度、提高定位可靠性的有效性。 本文基于对两种常用RAIM方法的研究比较,提出一种基于两种不同RAIM方法的改进奇偶空间方法,提高算法的运算效率,更加适合星载GPS接收机使用。并对该方法进行工程实现和平台验证,结果表明:利用该改进奇偶空间方法能够有效地进行故障星的检测与识别,且在满负荷运算的情况下,即在导航星数目为12颗时,改进后的方法运行时间仅需24.8 ms,相比奇偶空间方法运行时间减少10 ms,运行效率提高25%,更加适合星载GPS接收机的在轨应用。1.2 基于奇偶空间矢量的RAIM算法
2 RAIM算法改进研究
2.1 最小二乘残差方法与奇偶空间方法的比较

2.2 改进方法

3 改进方法验证

3.1 运行时间比较

3.2 定位精度验证


4 结束语

