一种正样本单分类框架下的高分辨率遥感影像建筑物变化检测算法
刘 波,燕 琴,刘恒飞,马 磊
(1. 兰州交通大学 测绘与地理信息学院,甘肃 兰州 730070; 2. 甘肃省地理国情监测工程实验室,甘肃 兰州 730070 ; 3. 国家测绘地理信息局,北京 100830; 4. 国家测绘地理信息局黑龙江基础地理信息中心,黑龙江 哈尔滨 150081)
随着近年来高分辨率遥感影像的快速发展,尤其是国产高分卫星的相续升空,高分影像的时间分辨率与空间分辨率均得到了较大的提升,因此研究基于高分辨率遥感影像的建筑物变化检测具有重要的实用价值。
目前,基于高分辨率遥感影像的建筑物变化检测得到了学者们的大力关注,如文献[1]利用建筑物与阴影的关系,通过一种概率模型的方法识别建筑物变化区域;文献[2]则从边缘的角度出发,结合建筑物的空间几何结构,识别建筑物的变化情况;针对高分影像存在的同谱异物现象,文献[3]提出利用纹理特征加以辅助进行改善,并结合形态学运算取得较好的实验结果。然而上述方式都是仅从浅层的特征角度出发,识别建筑物变化情况,对于复杂的建筑物几何结构难以达到较好结果,针对这一不足之处,挖掘深层次建筑物空间结构特征则成为了研究重点。文献[4]提取了一种简单高效的建筑物空间特征—形态学建筑物指数(Morphology building index, MBI),利用该指数在高分辨率遥感影像上进行建筑物识别,得到较好的实验精度。MBI在建筑物变化检测中早已运用,但在进行变化检测时都需要人工设定简单阈值并还需要进行后续处理才能获取较高精度的检测结果[5]。
近年来,机器学习方法在各行各业中得到了充分的应用,其在遥感影像变化检测中也正不断被学者们采用。传统的方法是通过选择训练样本的方式完成变化的判定,这种方式虽然可以克服很多复杂条件,但需要人工选择正负样本,效率相对较低。
文献[6]利用一种单分类器,将其成功应用到中等分辨率遥感影像土地变化调查中,取得了较好的实验结果,从该思路出发,本文设计了一种正样本单分类框架下的高分辨率影像建筑物变化检测算法,其具有以下优点:①无需负样本的选定即可进行变化判决。②设计了一种新的形状描述算子,对后续结果进行优化,提升了最终的检测精度。
1 单分类框架下的建筑物变化检测
本文的实验流程主要包括以下步骤:首先从建筑物的特征挖掘出发,引入一种形态学建筑物指数进行建筑物特征描述,然后利用卡方变换进行多特征融合,同时采用叠加联合分割的手段完成地物影像对象提取,最后利用一种正样本单分类器,以众数规则的方式完成对象级变化检测。其中,本文的建筑物变化检测实验流程如图1所示。

图1 实验算法设计流程
1.1 建筑物空间特征提取
高分辨率遥感影像上相同地物间光谱差异变大,不同地物间光谱差异变小,相对于中低分辨率遥感影像的变化检测难度更大。针对这一问题,学者们在特征提取方面进行了大量的研究,以其改善仅依靠光谱特征的不足之处,如引入纹理算子—灰度共生矩阵(Gray level co-occurrence matrix, GLCM)等进行改善[7]。尽管该类方法取得了一定的效果,但是建筑物纹理呈现多样性,难以用一种或者多种纹理提取算子进行简单的描述。文献[7]从建筑物本身的光谱、几何等特征出发,提出了一种针对建筑物本身的特征描述子——形态学建筑物指数(Morphology building index, MBI)。该特征能够对影像上的建筑物区域进行增强,在建筑物识别等方面得到了广泛的应用,本文采用该算子作为建筑物的空间特征描述。
建筑物形态学指数计算主要包括以下几个步骤:
1)对于多波段原始影像,对每个像元光谱剖面,取最大值进行多波段合成,
(1)
式中:bandk(i)为波段k中像元i的灰度值,K为影像的波段总数,b(i)为合成后的单波段像元值,利用该式对多波段进行合成的主要目的是对不同颜色的建筑物屋顶进行增强。
2)利用顶帽变换的差分形态学剖面(Differential morphological profiles, DMPs)完成对建筑物的光谱结构特征描述。
TH-DMP(d,s)=|THb(d,s)-
THb(d,s-Δs)|.
(2)
其中
(3)
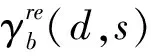
3)利用步骤(2)中的计算式,分别计算出的多个方向多个角度的差分形态学剖面,最后以取均值的方式完成建筑物形态学指数计算,
(4)
式中:MBI为计算出的形态学建筑物指数;D,S分别为线性结构元素的方向总数与尺度总数。
1.2 卡方变换多特征融合
变化向量分析(Change vector analysis, CVA)是一种经典的多特征等权融合方法[8],其计算方式简单,在变化检测中得到了极大的应用,
(5)
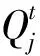
可以看出,变化向量分析对于各个特征波段只能利用等权的方式进行多特征融合,无法突出较优特征。因此研究一种自适应权重的多特征融合算法对于建筑物变化检测具有非常重要的意义。卡方变换(Chi-square transform, CST)是一种自适应权重的多特征融合算法,其在遥感影像变化检测中近年来得到了广泛的应用[8]。CST多特征融合主要通过将差分波段的方差作为融合权重:
(6)

从该式可以看出,基于卡方变换的多特征融合,能够自适应权重进行多特征融合,无需人工干预设定权重,利用本文提取的形态学建筑物指数特征与光谱特征进行波段组合,利用卡方变换的方式进行多特征融合,得到一个最终的变化波段,为了方便下一步计算,本文采用线性归一化的方法对其进行归一化,将值归一到(0,1)。
1.3 单分类框架下变化检测
利用卡方变换对多个特征波段进行融合,得到一个最终的多特征融合波段。通过一个简单的阈值设定对变化波段进行判定,然后得到变化与否,该种方式是一种高效简单的变化检测方式,但是该种方式通过对全局用一个阈值设定来进行判定,最优阈值的选取难以确定,难以得到最优结果。通过机器学习的方法来对全局进行统计建模,理论上能够得到更优结果[9]。基于机器学习的变化检测,通常需要人工选取训练样本,且同时需要正负样本的加入,即人工选取一定的变化与未变化样本,效率方面具有一定的局限性。
文献[9]通过对现有基于机器学习的变化检测方法进行分析,引入了一种只需正样本的分类器——支持向量数据描述(Surpport vector data description, SVDD),即仅仅需要人工选取变化样本即可,无需选取未变化样本,降低人工干预,且得到较好的实验效果,计算效率方面也得到了较大的提升,其在中等分辨率制图方面得到成功的应用,借鉴于此思想,本文将其运用到高分辨率遥感影像上。
SVDD最早是用来解决有偏数据的单分类问题,大量研究表明,该单分类器的实验效果达到了经典的两类支持向量机(Surpport vector data machine,SVM)同样效果,且在大数据量的情况下,计算效率更高[10]。考虑到SVDD的上述优点,本文选取该分类器作为本文的正样本单分类器,通过人工选取少量变化样本,来完成建筑物变化检测。
1.4 基于对象的变化检测
用上述单分类器得到建筑物的初始变化检测,由于其是从像元的角度出发,因此不可避免的产生大量空洞与椒盐现象,针对这一问题,本文通过面向对象的方式进行改善。首先,本文利用一种自底向上的分割算法,完成对地物的对象建模[10],然后利用下式完成对象级变化检测结果判定:
式中:i为分割后的某一对象,num()为对象内满足某一条件的像元个数。根据上式实现面向对象的变化检测,有效地改善空洞等现象。
1.5 进长宽比形状特征
初始变化检测后的结果中,通常包含较多其他地物类变化,如道路等,为了得到更为准确的建筑物变化检测结果,文献[4]提出了首先对二值图像进行连通区域标记,然后利用长宽比等形状特征进行道路去除,从而得到更为理想的实验结果,该种方法在一定实验情景下得到去除道路网络,但是对于环形或者更为复杂的道路网络,难以进行有效去除,针对这一问题,本文提出了一种改进的长宽比形状特征来更好地对道路等其他非建筑物变化类进行有效去除。
其中本文改进的长宽比不再以最小外接矩形的长度作为判定,而是以对角线作为长宽判定,对于这种交叉路段或者环形道路能够更好地进行去除,其中本文改进的长宽比:
(7)
其中:length为连通区域最小外接矩形的长度,width为连通区域最小外接矩形的宽度。
2 实验分析与讨论
为了验证本文算法的有效性,本文分别从以下三个角度进行了算法对比分析:①与传统的监督分类方法进行了对比分析,即同时选择正负样本。②与目前其他较优建筑物变化检测算法进行对比。③与其他正样本单分类器算法对比。其中本文实验数据为成都市某地区,其中相关参数说明和真实数据如表1所示。

表1 实验数据介绍
两期影像均经过严格的几何校正与直方图辐射值匹配,保证两期影像后续处理的精度需求,如图2所示,图2为真实影像数据。
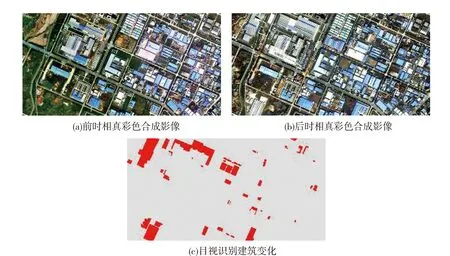
图2 实验数据集
首先与传统的监督分类方法对比,本文选择经典的SVM方法,其中核函数选择为RBF,参数C,g通过交叉验证得到最优,正负样本均选取真实样本的5%。其次选择文献[4]提出的算法,其中光谱判别阈值为0.2,MBI判别阈值为0.3,长宽比阈值设定为10。最后选择与正样本单分类器算法对比,本文主要选择文献[6]使用的算法进行对比,其分类器选择为SVM,负样本自动生成比例为1,其中人工勾选的正样本75%用于训练,25%用于测试,后验概率判定阈值均设置为0.5。本文算法中,选取5%变化区域为正样本,改进长宽比阈值设置为10。不同算法对比实验结果如图3所示。
从实验结果来看,本文算法取得了相对较优的视觉效果,文献[4]提出的建筑物变化检测算法由于其仅仅从像元的角度出发,因此导致了大量的椒盐现象,且简单的阈值设定难以得到非常理想的实验结果。文献[10]提出的单分类算法与本文算法效果类似,但是其仍然有部分并没有识别出来。而与经典的SVM两类方法对比,本文方法错误识别较少。
为了更好地验证不同方法对比,本文参照文献[4]采用定量的精度评价方法,其中有三个重要的指标,正确率(Correctness, CT)、虚检率(False alarms, FA)、漏检率(Miss alarms, MA)。定量对比精度结果如表2所示。
从表2中可以看出,本文算法三个指标均取得了较优结果,文献[6]提出的单分类方法由于漏识别部分较多,因此漏检率较高,从具体的单分类实现算法原理来看,这是由于其负样本为全局自动生成,部分正样本可能被误判别为负样本,导致精度降低。文献[4]从像元的角度出发,实验结果产生较多的空洞与椒盐现象,这是由于其以单个阈值的方式来判定全局的变化,难以确定,且高分辨率遥感影像上,同谱异物现象严重,因此容易产生较多的误识别像元。从最后定量的精度评价结果看,本文的单分类方法取得了较二分类更优的结果,在有限样本数据下,验证本文的单分类方法是可行的,且具有较高的精度。

图3 不同算法实验结果
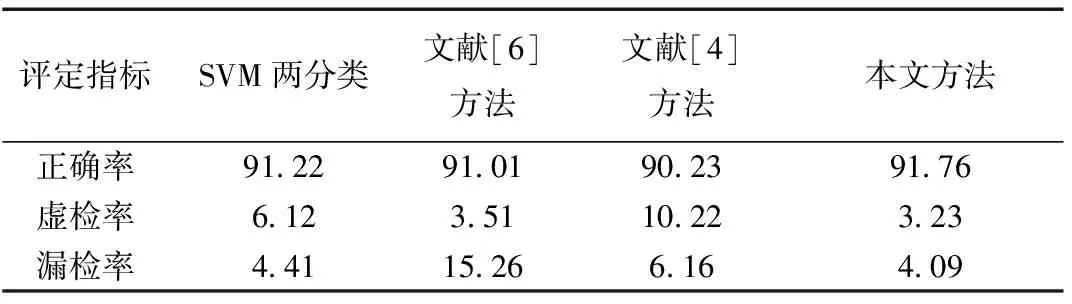
表2 不同算法精度定量对比 %
3 结束语
本文针对现有基于机器学习的建筑物变化检测算法,需要人工标注正负样本,为减少了人工干预,引入了一种单分类器,无需负样本的选取即可完成建筑物变化检测,且具有较好的实验结果。针对非建筑物变化区域,本文利用改进的长宽比特征进行过滤,提高了最终的提取精度。从算法实现的角度来看,本文仍然需要人工选取正样本,下一步会将重点放在如何自动获取正样本的研究上,从而完成全自动的高精度建筑物变化检测。

