基于弧段的遥感专题信息图斑分段平滑方法
高 倩,章孝灿,胡 祺
(浙江大学 地球科学学院,浙江 杭州 310027)
栅格数据和矢量数据是地理信息系统中常用的两种数据。栅格数据是一种离散的点阵数据,每一个单元的属性值代表实体属性,具有数据结构简单,易于进行空间分析等优点,但是数据存储量太大,缩放尺度有限制。矢量数据由点的精确坐标来表达点、线、面等地理要素,具有数据存储量少,放大缩小不失真,精确定位等优点。由于矢量数据有存储空间小,便于观察,具有空间对象,可以精确定位等较于栅格数据的优点,在实际生产中常常需要将栅格数据矢量化。栅格矢量化通常分为两种,一种是线状数据的矢量化,比如等值线图,另一种是图斑的矢量化,比如遥感分类图,专题图等都需要栅格矢量化。本文主要讨论图斑矢量化后的问题。栅格矢量化后,由于栅格数据具有点阵特点,是离散性数据,矢量化后的数据呈现锯齿状,十分不美观,与实际地物的连续边界不符,且造成大量的数据冗余。为了矢量化后图斑的美观性、真实性,以及减少数据的冗余,节省数据的存储空间,需要对矢量化后的数据进行平滑。
目前多边形平滑算法可以分为3类。一类是矢量抽稀算法[1-8],将数据抽稀,以达到减少数据冗余且平滑的结果。主要方法有垂距法,光栏法,道格拉斯普克(Douglas-Peucker , D-P)算法,小波算法,遗传算法等。其中D-P算法是最常用的一种,自提出以来不断被改进,如黄万里等提出的基于面积保持的D-P算法[9],顾腾等提出的D-P算法与Li-Openshaw结合改进的方法[7]。虽然矢量抽稀算法能有效平滑锯齿,消除数据冗余,但是往往需要一个适合的阈值,阈值的大小难以把握。第二类是曲线拟合算法[10-12],如多项式拟合,B样条拟合,贝塞尔曲线等,曲线拟合是平滑多边形最常用方法。然而曲线拟合难以去除图斑锯齿,反而会出现“波浪”。第三类是综合法,将多类方法结合使用,比如前面提到的D-P算法和Li-Openshaw结合的方法,D-P算法和B样条结合的方法[13]等,此类方法因结合多种方法计算缓慢。
由于图斑中锯齿的存在,上述3种多边形平滑方法无法较好地平滑图斑。加之遥感图斑通常具有实际意义,特别是土地利用类型图斑的面积属性,在实际应用中有重要意义,平滑后图斑与原始图斑面积和位置的保持十分重要。此外,若相邻图斑公共边处理不一致,容易出现“裂缝”等拓扑错误的结果。因此,需要提出具有针对性的图斑平滑方法。石军南等人提出的矢量线条概率中值平滑方法[14],宋正祥等人提出的顾及拓扑与尖角的矢量数据分组压缩算法都是针对图斑的平滑[15],均达到了良好的平滑效果,但无法保持原始图斑面积和位置。综上图斑的平滑存在3个问题: ①图斑呈现锯齿状;②平滑时难以保持图斑面积及位置信息;③平滑时图斑公共边易出现拓扑错误。
针对上述问题,以矢量化后的图斑为研究对象,考虑到相邻图斑的拓扑关系,以及图斑平滑前后面积和位置保持的问题,提出基于弧段的遥感信息图斑分段平滑方法。通过对矢量化后图斑的弧段进行分段后再平滑,达到保持其拓扑关系,也保持原始图斑面积和位置的结果。
1 基于弧段的分段平滑方法
基于弧段的遥感专题信息图斑的分段平滑方法利用深度搜索的方式提取弧段,防止后续平滑出现拓扑不一致的结果,再根据锯齿梯度对弧段分段,然后进行平滑,以降低矢量化后数据平滑造成的面积和位置的偏差。
1.1 弧段提取
栅格矢量化后的数据没有拓扑结构,平滑时相邻图斑的公共边平滑不一致,容易产生如图1所示的“裂缝”,“重叠”等拓扑不一致的结果。但是在拓扑结构下,相邻图斑的公共边共用一条弧段,仅平滑一次,则避免了平滑不一致产生的拓扑错误。为消除平滑时容易出现的拓扑错误,采取深度搜索的方式提取弧段,为后续平滑做准备。

图1 有公共边的平滑
实验数据为常用ArcGIS的shp矢量文件,shp文件没有拓扑结构,按数组顺序存储多边形,多边形外环的点顺时针存储,多边形内环的点逆时针存储。针对shp文件的特点,以及深度搜索方法[2-3, 16]的特点,提出以下方面修正,使其更适用于shp文件,流程如图2所示。

图2 弧段提取流程
1)深度搜索采取“顺序比较”和“逆序比较”的方法搜索公共边。在shp文件中,公共边在相邻图斑中必然是顺序相反,因此只需要逆序比较。
2)搜索时起始点为第一个存储点,不是弧段的端点。如图3所示,图斑AB在公共边均有图斑存储的起始点与终止点,于是除了“逆序比较”找到end点,还要将start点向前移动。即A多边形的点1,2,3,…,比较B多边形i,i-1,i-2,…,找到end点,还需要A多边形的点n,n-1,n-2,…,比较B多边形i,i+1,i+2,…,找到真正的start点。

图3 图斑中点的存储
3)搜索到一段弧段时立即平滑替换掉原始弧段,并标记,再次搜索到该弧段时,不需要二次对比,直接跳过。
4)弧段仅需平滑一次,若是公共边的弧段,在另一图斑中只需将平滑后弧段逆序存储替换掉原始弧段。
1.2 弧段分段平滑
栅格矢量化后,由于遥感图像的点阵特点,栅格数据对边界的表达有限,矢量化后的图斑存在大量锯齿。图斑不美观和数据冗余都由锯齿造成,于是平滑图斑只需对锯齿平滑,即可达到平滑效果。采取将弧段分段为平滑锯齿单元的方式找到需要平滑的锯齿,采用锯齿中线代替锯齿的方式进行平滑,达到既平滑图斑,又保持图斑面积和位置的结果。
1.2.1 平滑方式
如图4所示AB两图斑,公共边为锯齿。提到栅格数据转换为矢量数据时,线条形状变化,其特点分布概率不确定,栅格数据矢量化的曲线是一条栅格线条的中线时方差最小。在图斑中同样,如图4所示,锯齿为AB两图斑的交接处,线1和线3包围区域为锯齿所属范围,同时为既有图斑A也有图斑B的混淆地带。在线1和线3包围区域内的线都能将此区域等分为两份来替代锯齿,但是中间线线2为锯齿边最佳拟合的直线,其残差最小。线2可使该交叉地带一分为二,使斑AB位置不偏移,面积也能保持一致。不难发现,若需要平滑后AB两图斑面积保持一致,中线需平分锯齿,为保证左右分到的面积相等,中线的起始点在水平线(垂直线)上,终止点也应在水平线(垂直线)上。如图4所示,可以保证AB图斑面积不变,这样中线左右两边的点数相同,面积也相同。

图4 锯齿边界分析
1.2.2 弧段分段
1)平滑锯齿单元。单纯地使用中线进行锯齿平滑,保持原状的边也进行处理,且未考虑到平滑后图斑面积保持的问题。如图5(b)中弧段的2~3处,此处数据不进行处理,也能去除锯齿且更能保持原始数据。为了减小平滑后数据的偏差,在平滑时此类数据不应平滑。由此,提出将锯齿弧段分段为平滑锯齿单元,平滑锯齿单元为连续的相同梯度的锯齿,仅对平滑锯齿单元进行平滑处理,这样就能在去除锯齿的同时尽量减少平滑对数据造成的偏差。

图5 一般去锯齿算法
相关概念定义如下,平滑锯齿单元:相同梯度的锯齿边分割为一个平滑锯齿单元,如图5(b)中弧段的1~2处为一个平滑锯齿单元。锯齿边:相邻三边,中间边为单位像元长,前后两边走向一致,则为锯齿边,如图6(a)所示。锯齿梯度:相邻三边,中间边为单位像元长,前一条边与中间边长度的比值为锯齿梯度。
2)平滑锯齿单元分割方法。由上述思想,提出一种平滑锯齿单元分割方法。设弧段上点的坐标为(Xi,Yi),相邻点横坐标差值|Xi=Xi+1|X,纵坐标差值|Yi=Yi+1|Y。因为锯齿弧段都是由水平或者竖直线段组成,所以相邻两点有且仅有一个为0,因此相邻两点组成的线段长度L(i,i+1)=|ΔXi|+Yi,,且L(i,i+1)的正负代表其走向。平滑锯齿单元分割方法如下:
步骤1:对弧段进行冗余点去除。遍历弧段上所有点,连续3个点在一条直线上时,中间点为冗余点,需去除,然后进入步骤2。
步骤2:依次遍历弧段上的点,计算相邻4个点的关系,当条件:L(i-1,i)×L(i+1,i+2)>0,且|L(i,i+1)|的值为单位长时,分以下3种情况,不满足条件时为线段标注0:
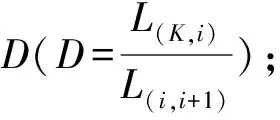
②如图6(b)所示,若|L(i+1,i) 图6 3种情况 步骤3:标注完成后,当标注连续数字相同且大于0的边分为一个平滑锯齿单元。如图7(a)弧段可以分为三段,平滑锯齿单元1~2,平滑锯齿单元3~4,非平滑锯齿单元2~3。 图7 弧段分段平滑 步骤4:平滑。平滑锯齿单元进行平滑处理。非平滑锯齿单元保持原始数据。如图7(b)所示弧段分段平滑后。 将分辨率为30 m的Landsat8遥感影像经过非监督分类为5类,得到分类图见图8(a),将其栅格矢量化后得到图8(b),以图8(b)为实验图。 图8 实验数据 为了表明方法的有效性,实验对比3种用在图斑平滑中的算法,分别是概率中值算法[14]、D-P算法[2]( D-P算法使用的压缩阈值为30)、去尖角算法[15]。3种算法及文中提出的方法均在Visual Studio 2010下用C++语言利用GDAL库编程实现,对 shp 文件格式的矢量实验图进行处理。平滑结果如图9所示。 图9 实验结果 为了比较算法间的优缺点,实验对比分析面积保持和位置保持效果以及平滑程度和压缩率这4个方面的效果,统计结果见表1与图10,分析方法如下: 1)平滑程度分析。平滑程度除了可以从目视效果看出,还可以从尖角(0°~90°或者270°~360°的角)数量得出,尖角数越少越平滑。 2)面积保持效果分析。对平滑前后的面积作比较,计算各个图斑的面积变化率,用平滑后的面积减去平滑前的面积得到面积差,面积差除以原始面积得到图斑的面积变化率。实验统计面积变化率的最大、最小值和均值,统计结果见图10。 3)位置误差分析。通过缓冲区限差[17]对位置误差进行分析,缓冲区限差是对原始弧段建立缓冲区,统计平滑后弧段完全落入对应原始弧段缓冲区里的弧段数占总弧段数的比例,用此比例来评价位置的保持情况,比例值越大,位置保持越好。 缓冲区限差: (1) 式中:Ln为落入相应原始弧段缓冲区的平滑后弧段数,L为总弧段数。 在统计落入缓冲区的弧段时,为保证相邻弧段的缓冲区不会相交,对原始弧段建立半个像元距离的缓冲区。 4)压缩程度。以平滑后的总点数与原始总点数之比的压缩率来评价平滑前后的压缩程度。 5)时间效率。统计4个方法计算同一数据的计算时长,以此来比较4个方法的时间效率。计算时长越短计算效率越高。 表1 4种方法平滑程度、位置误差、压缩率、时间效率的评价结果 图10 面积变化率 观察上述实验结果,图9可以清楚观察到4个算法平滑结果,仅目视效果而言,D-P算法呈现大量尖角,并不是很美观。去尖角算法虽然去除了D-P算法的大部分尖角,但是由不同公共边共同形成的尖角却未能去除。通过表1中的对尖角的统计,可以看出分段平滑方法平滑程度最高,D-P算法平滑程度最低。由图10 和表1中面积和位置的统计结果可以看到,分段平滑方法平滑前后面积保持了一致,而且弧段均在缓冲区内,分段平滑方法面积与位置保持是最优的。D-P算法是位置和面积保持最差的,但是在压缩程度上D-P算法有着绝对的优势。可见D-P算法对图斑的压缩平滑,在面积和位置信息上有所牺牲。另外两个算法的压缩率和面积位置保持都介于D-P算法和分段平滑方法之间。时间效率上去尖角算法是在D-P算法基础上进行了尖角去除,时间效率上比D-P低,本文算法较另外3种方法稍稍高一点。综上所述,几种方法虽然都能有效平滑,但是在平滑程度,面积保持,位置保持以及计算效率方面文中提出的方法最优。 本文针对遥感信息图斑边界呈现锯齿状,提出一种基于弧段的遥感专题信息图斑分段平滑方法,用深度搜索的方式提取图斑弧段,根据锯齿弧段的梯度分段为平滑锯齿单元,对平滑锯齿单元进行平滑处理,以达到平滑弧段、图斑面积与位置保持之间平衡,为遥感分类图,专题图等矢量化后提供一种平滑方法。该方法减轻了以往方法平滑后对原始数据造成的偏差,但平滑后数据冗余消除程度远不及矢量抽稀算法。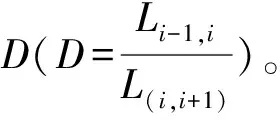


2 实验与讨论




3 结束语

