全球电离层延迟建模及精度分析

王 健，党亚民，王 虎

(1.山东科技大学 测绘科学与工程学院，山东 青岛 266590；2.中国测绘科学研究院，北京 100830)

电离层主要指高出地面60～1 000 km的大气层区域，该层在太阳紫外线、X射线、γ射线和磁层中高能粒子对大气中性气体分子等的共同作用下形成一个整体呈电中性但其中包含大量自由电子和正负离子的区域[1-3]。电离层可以反射低频无线电信号，也可以改变穿过其区域的高频无线电波的传播方向、速度等性质，所以研究电离层对人类空间活动具有重要意义。

自GPS建立以来，电离层延迟误差已成为影响全球导航定位精度的重要误差源，并且还会给卫星通信等科研应用领域带来不可忽视的影响[4-7]。消除电离层延迟误差始终是电子通讯及导航定位领域研究的热点问题。国内诸多学者也对此进行研究分析。文献[8]就鞍山CORS站的GNSS双频载波相位观测资料和伪距观测资料构建覆盖该区域上空的电离层模型。实验表明在小范围内，模型的不同阶数设置对模型精度的影响不是非常明显。文献[9]采用GPS单系统和融合BDS/GPS/GLONASS三系统两种方案，采用载波平滑伪距观测值和球谐函数，构建全球电离层延迟模型对比分析后结果表明：三系统融合反演全球电离层在精度上优于GPS单系统，均有5～10 TECU的提高。本文详细介绍全球电离层延迟模型，采用中国测绘科学研究院iGMAS分析中心数据，建立全球电离层延迟模型，并对建模结果以及频间偏差结果进行比较与精度分析。

1 建立全球电离层延迟模型

在GNSS测量中，电离层延迟误差在天顶方向能达到3～9 m，而在接近地平方向电离层延迟误差可达到150 m，这也是结束SA政策后GPS定位中最大的误差源之一,所以能否有效削弱电离层延迟误差的影响，决定着所有GNSS用户导航定位精度与可靠性指标。目前为了消除或减弱电离层影响，国内外采用的主要措施是电离层延迟模型改正法，电离层模型就是利用电子浓度剖面解析式来减弱电离层延迟的方法[10]。在GNSS导航定位中一般有以下两种电离层延迟改正模型：经验模型和理论模型。经验模型由大量电离层探测资料统计而得，可以描述平静电离层状态的统计模型，它对许多和电离层特征参数相关的数据进行统计，经过数据处理得到若干不同电离层经验模型，其中应用最广泛的有国际参考电离层IRI模型、Bent模型和Klobuchar模型[11]，理论模型主要是电离层内部分子的形成特点以及电离层物理化学机理推导得到，全球电离层模型的研究把它作为强有力手段，本文依据理论模型，采用中国测绘科学研究院2016年年积日190天112个测站数据，建立全球电离层延迟模型，且效果较好。

本文采用伪距和相位观测值进行载波相位平滑伪距，进而得到高精度的绝对TEC[12-13]。

c(DCBr+DCBs)}.

(1)

式中：f1,f2表示双频载波相位的频率；N为一个连续弧段的历元数；P2,P1和L1,L2表示伪距和载波相位观测值；DCBr,DCBs表示接收机和卫星的差分码偏差。

对于同一电离层，测站到各个卫星的传播路径不同，所以不同方向上具有不同的TEC值，其中，天顶方向的总电子含量VTEC的值最小[14]。一般采用单层电离层投影函数将无线电信号传播方向上的电子含量STEC投影到天顶方向得到VTEC[15]：

(2)

其中VTEC为垂直方向电离层电子含量，z′为卫星在穿刺点(假设电离层压缩为一个单层，所有电子都位于该层，称为中心电离层。卫星传播路径与中心电离层的交点称为穿刺点IPP,如图1所示)处的天顶距，z为接收机处的天顶距，R为地球半径，H为假设的电离层薄层厚度。

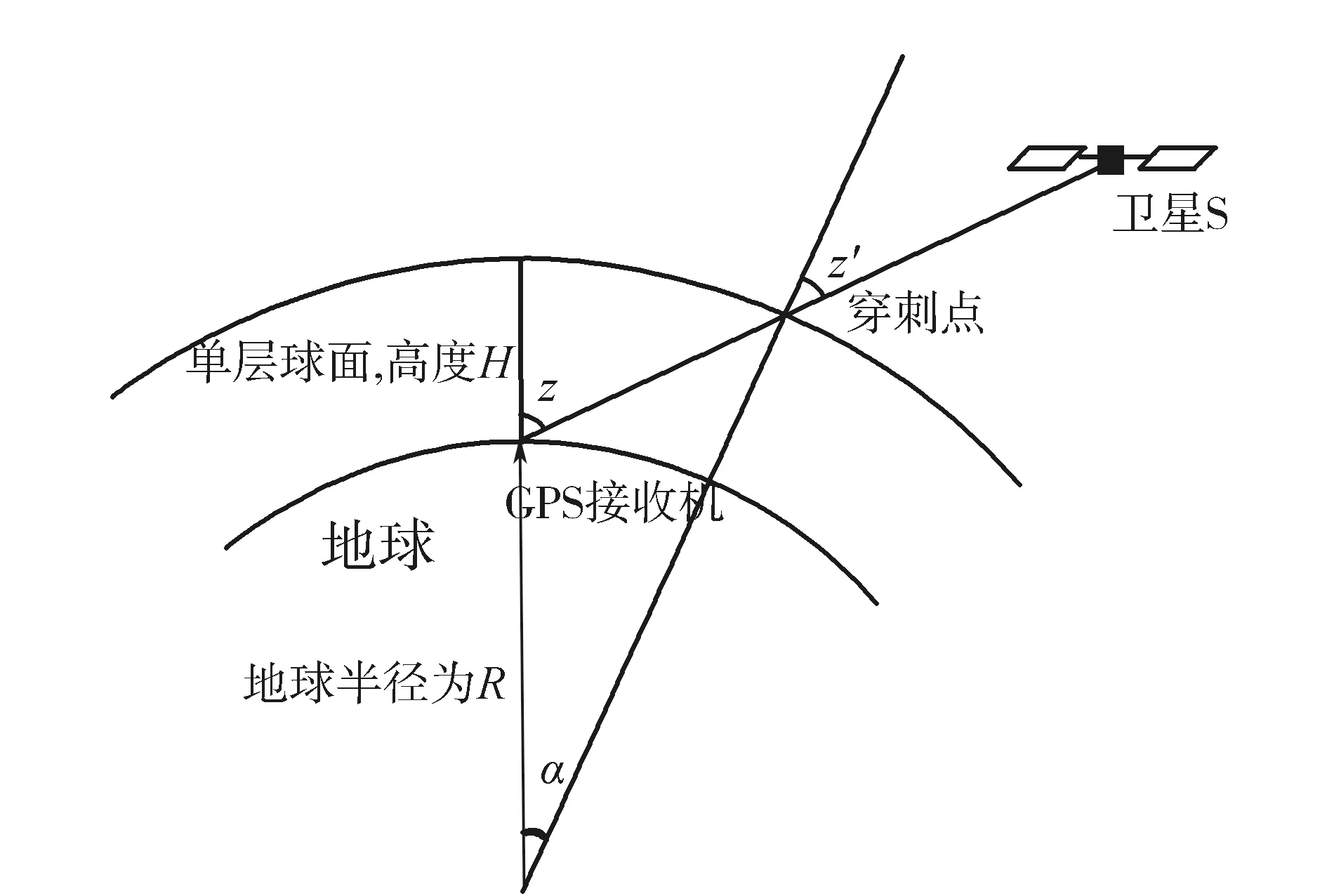
图1 电离层单层模型

将不同的观测手段得到的VTEC值，采取合适的模型进行拟合可获得电离层模型[16-18]。本文采用球谐函数模型获取VTEC值。

bijsinjλ).

(3)

式中：ρ为电离层穿刺点IPP的地理纬度，λ为电离层穿刺点IPP的日固经度，imax为球谐函数的最高阶数，j为球谐函数的阶数，Pij(cosρ)=Nij·Pij(cosρ)为i度j阶的缔合勒让德多项式，Nij是归化函数，即

(4)

δ0m为Kronecker型的δ函数，当m≠0时，δ0m=0，当m=0时，δ0m=1；aij和bij表示电离层球谐模型的待求参数，不同的时刻aij和bij值也不同。如果知道某时刻aij和bij，可以由式(3)计算出该时刻地面上空相同高度球壳上纬度ρ、经度λ的电子浓度。

2 观测资料分析

2012年底，由中国主导的国际GNSS监测评估系统(international GNSS Monitoring and Assessment System,iGMAS)，向广大科研院所提供高精度全球电离层TEC格网产品，iGMAS电离层分析中心包括中科院测量与地球物理研究所、武汉大学、中国测绘科学研究院等10多家单位。本实验采用中国测绘科学研究院(CASM)分析中心2016年年积日190 d 112个测站数据进行全球电离层延迟模型的建立，其中建模阶数为15阶。站点如图2所示。由图2可看出站点基本可以实现均匀分布。

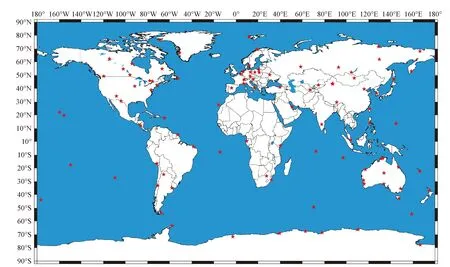
图2 站点分布

3 全球电离层建模结果及分析

3.1 格网TEC分析

对2016年年积日190 d的数据进行处理，并计算电离层延迟。图3为采用曲面拟合模型的建模流程图。首先将计算结果中UTC时为2:00、10:00、18:00时刻电离层结果制图(见图4)。将计算结果与IGS分析中心(CODE)电离层产品进行精度比较，两者残差图如图5所示。

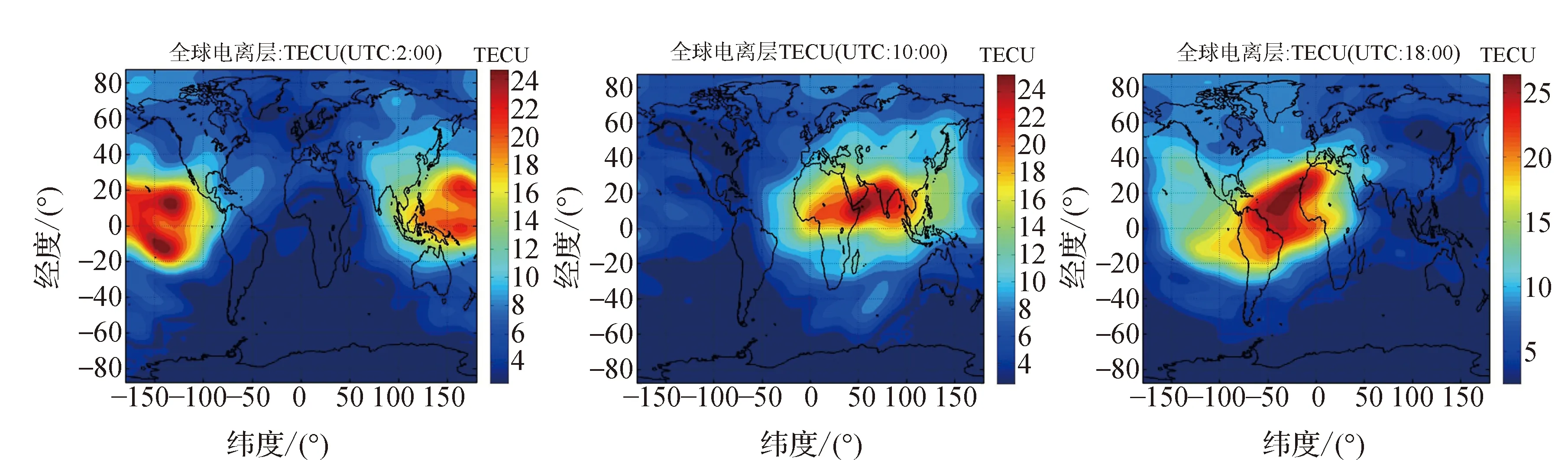
图4 不同时刻电离层总电子含量

图5 不同时刻电离层总电子含量与CODE做差图

由图3可以看出：全球电离层延迟建模结果基本在25 TECU以内，大部分在0～15 TECU之间。且电离层TECU最大值的区域不同。由图4可以看出：全球电离层球谐函数建模结果与CODE差值基本在0～4 TECU之间。大陆地区精度最高，基本在1 TECU以内，海洋地区以及南半球部分地区精度较差，最大能达到4TECU，均值在3TECU以内，可能是海洋附近测站较少的原因。

3.2 频间偏差结果及分析

全球电离层延迟建模中频间偏差产品一般按天解算， 模型精度可由其求解的精度直接反映。计算2017年7月份共31 d的卫星C1-P2频间偏差产品，并求平均值，得到各卫星频间偏差的平均值，如表1所示。

表1 GPS/GLONASS系统卫星DCB月平均值 ns

以CODE中心7月份发布的卫星频间偏差月产品为参考，将本文计算结果与之做差，结果如图6所示。由图6可知：各卫星C1-P2的DCB结果与CODE差值在0左右波动，大部分在1.5 ns以内，说明本文的GPS/GLONASS卫星系统DCB精度与CODE相当，也反映本文建立的电离层延迟模型精度较高。

图6 GPS/GLONASS系统卫星DCB与CODE差图

4 结 论

本文介绍利用中国测绘科学研究院iGMAS分析中心数据建立全球电离层延迟模型的方法和结果。得出以下结论：

1)全球电离层球谐函数建模结果与CODE差值基本在0～4 TECU之间。大陆地区精度最高，基本在1 TECU以内，海洋地区以及南半球部分地区精度较差，最大能达到4 TECU，均值在3 TECU以内，可能是海洋附近测站较少的原因。

2)各卫星C1-P2的DCB结果与CODE差值在0左右波动，大部分在1.5 ns以内，说明本文的GPS/GLONASS卫星系统DCB精度与CODE相当。