总体矩阵法在水电站频率调节稳定性分析中的应用

马安婷，杨建东，杨威嘉，唐韧博，冯文涛，侯亮宇

（1. 武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2. 广东省水利电力勘测设计研究院，广东 广州 510635）

1 研究背景

水电站水轮机调节系统通常由调速器、水轮机、有压输水系统、发电机和电网构成，其运行稳定性是由管道布置方式、机组运行工况点、调速器参数等多种因素决定的，是一个有条件稳定系统［1］。传递函数法是进行输水发电系统稳定性分析的重要方法，在以往的研究中，常采用简化的单管单机布置方式及简化的一阶刚性水击模型求取系统闭环传递函数得到运行稳定性，但该方法不适用于一洞多机等复杂管道系统建模及分析。

水轮机模型可分为线性水轮机模型、非线性水轮机模型。在运行稳定性的研究中，往往采用线性水轮机模型。陈嘉谋等［2］、戴敏等［3］、马薇［4］采用Simulink 建立了复杂管道系统的数学模型，分析了线性水轮机模型下调节系统的稳定性和调节品质。郭文成等［5］推导了3 种不同调节模式下带调压室水电站的传递函数，分析了不同因素作用下稳定域的变化情况。Yang 等［6］研究了由调压室涌浪引起的低频振荡，并建立功率调节与频率调节相互切换的调速器模型。刘昌玉等［7］考虑到调压室振荡效应和分叉管水力耦合影响，建立了水轮机及调节系统精细化模型。俞晓东等［8］对水电站联合运行进行了小波动稳定性的研究，研究表明电站联合运行有利于增加系统稳定性并改善调节品质。索丽生［9］、郑向阳［10］、俞晓东等［11］采用状态空间法分析了水力机械系统小波动过程，状态空间法是通过推导小波动线性微分方程组，求解系数矩阵的特征值和特征向量判断系统的稳定性，但推导过程较为繁琐。已有的研究中侧重于对复杂管道系统进行Simulink 建模或者运用状态空间法进行系统稳定性分析，存在不能准确求解系统稳定域和建模推导过程繁琐等问题。

为了方便管道系统水力振动频率分析，Wylie 等［12］提出水力阻抗法，但管道系统较为复杂时，节点阻抗的推导也较为困难。乔杜里［13］在水力阻抗法的基础上提出了传递矩阵法，冯文涛［14］、段炼等［15］提出了便于编程的总体矩阵法，推导了特定条件下水轮机的水力阻抗和调压室阻抗，并用于复杂管道系统的水力振动研究。叶复萌等［16］通过阻抗法模拟阀门的自激振动，并与特征线法进行对比。Suo 等［17］提出了将频率响应转化为时域响应的脉冲响应方法。Kim［18-19］提出了更加通用的阻抗矩阵法（IMM），该方法可用于复杂非均匀管网。通常用特征线法对管网系统暂态过程进行分析，Ranginkaman［20］使用了传递矩阵法对一个真实的管网系统分析其频率响应，并论证了传递矩阵法与特征线法具有同样高的精度。Vítkovský［21］提出了基于拓扑矩阵的方法，该方法用于任意拓扑结构的管网频率分析，并考虑了黏弹性管道材料和非弹性摩阻的影响。周建旭［22］引入机组和调速器的动态特性，得到水力阻抗表达式，但没有将其运用于复杂管道系统稳定性分析中。

鉴于以上研究现状以及分析复杂管道系统水电站运行稳定性的需求，本文首先推导了完整的机组阻抗表达式，然后借用水力系统振动特性分析方法，建立系统总体矩阵，并以最大衰减因子σmax是否小于0 作为稳定性的判别依据。本文的方法能够准确求解复杂输水发电系统的稳定域，而且通过修改系统各个模块相应的传递矩阵排列顺序，本方法可适应不同的电站布置形式，极大地方便了水电站运行稳定性的计算与分析。

2 数学模型及判别条件

2.1 机组阻抗表达式的推导调速器采用频率调节［6］，PI 调节含Ty环节：

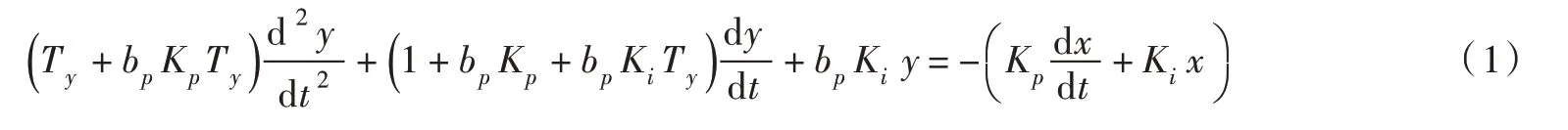
式中：Ty为接力器时间常数，s；bp为永态转差系数；Kp为比例增益；Ki为积分增益，s-1；y 为导叶开度偏差相对值；x 为转速偏差相对值；t 为时间，s。

水轮机力矩方程、流量方程［23］：

式中：mt、qt、h 分别为力矩、流量和水头偏差相对值；eh、ex、ey分别为水轮机力矩对水头、转速、导叶开度传递系数；eqh、eqx、eqy分别为水轮机流量对水头、转速、导叶开度传递系数。

发电机加速方程［23］：

式中：Ta为机组惯性时间常数，s；mg为发电机负载力矩偏差相对值；eg为发电机负载力矩随转速的变化率。

引水管道二阶模型［23］：

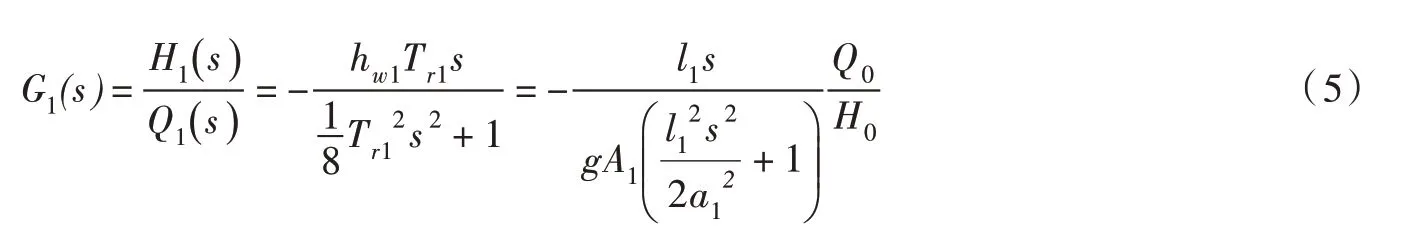
式中：G1为引水管道水击传递函数；H1为引水管道末端水头偏差相对值；H0为水轮机初始水头，m；Q1为引水管道末端流量偏差相对值；Q0为水轮机初始流量，m3/s；hw1为引水管道特征系数；Tr1为引水管道水锤压力波反射时间，s；s 为拉普拉斯算子， s=σ+iω；l1为引水管道长度，m；g 为重力加速度，m/s2；A1为引水管道面积，m2；a1为引水管道波速，m/s。

尾水管道二阶模型［23］：

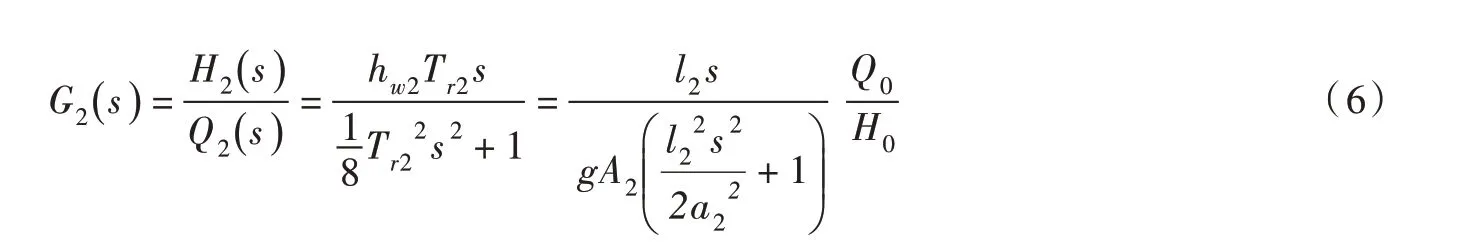
式中：G2为尾水管道水击传递函数；H2为尾水管道首端水头偏差相对值；Q2为尾水管道首端流量偏差相对值；hw2为尾水管道特征系数；Tr2为尾水管道水锤压力波反射时间，s；l2为尾水管道长度，m；A2为尾水管道面积，m2；a2为尾水管道波速，m/s。

对基本方程（1）—（4）进行拉普拉斯变换，得：

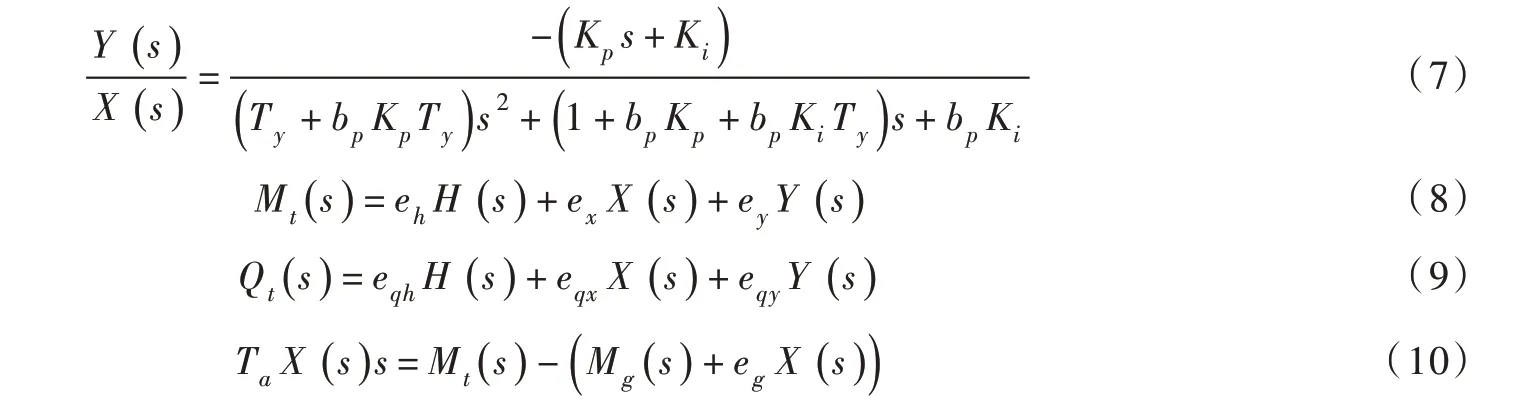
联立方程（5）—（10），可得出系统在负荷扰动mg作用下，单管单机水轮机调节系统的传递函数为：

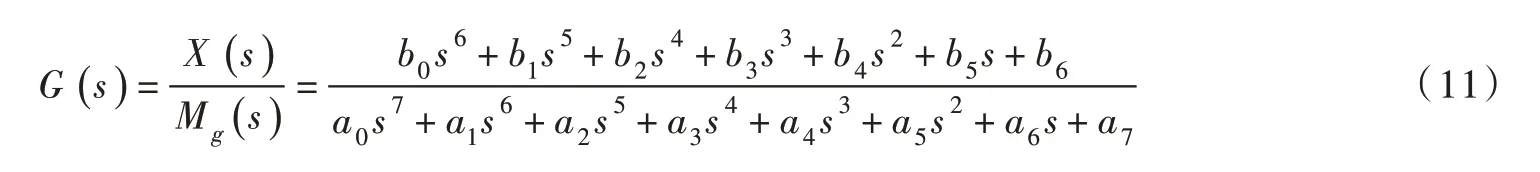
式中： a0=λ5λ18；a1=λ5λ19+λ6λ18；a2=λ5λ20+λ6λ19+λ7λ18+λ13λ21；a3=λ6λ20+λ7λ19+λ8λ18+λ13λ22+λ14λ21；a4=λ7λ20+λ8λ19+λ9λ18+λ14λ22+λ15λ21；a5=λ8λ20+λ9λ19+λ10λ18+λ15λ22+λ16λ21；a6=λ9λ20+λ10λ19+λ16λ22+λ17λ21；a7=λ10λ20+λ17λ22；b0=-λ1λ18；b1=-λ1λ19-λ11λ18；b2=-λ1λ20-λ2λ18-λ11λ19；b3=-λ2λ19-λ11λ20-λ12λ18；b4=-λ2λ20-λ12λ19-λ18；b5=-λ12λ20-λ19；b6=-λλ20；λ4=hw1Tr1+hw2Tr2；λ5=Taλ1；λ6=enλ1+Taeqhλ3；λ7=Taλ2+eneqhλ3+eheqxλ3；λ8=Taeqhλ4+enλ2；λ9=Ta+eneqhλ4+eheqxλ4；λ10=en；λ11=eqhλ3；λ12=eqhλ4；λ13=eyλ1；λ14=eyeqhλ3-eheqyλ3；λ15=eyλ2；λ16=eyeqhλ4-eheqyλ4；λ17=ey；λ18=Ty+bpKpTy；λ19=1+bpKp+bpKiTy；λ20=bpKi；λ21=Kp；λ22=Ki。其 中，en=eg-ex为水轮发电机组综合自调节系数。

将式（10）代入式（8），得：

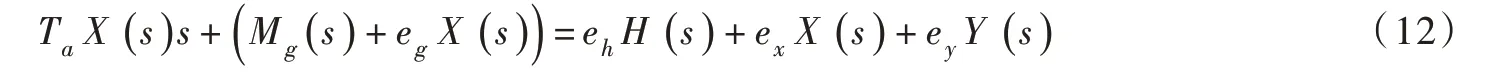
式（12）×eqy-式（9）×ey，整理得：

改写式（7），得：

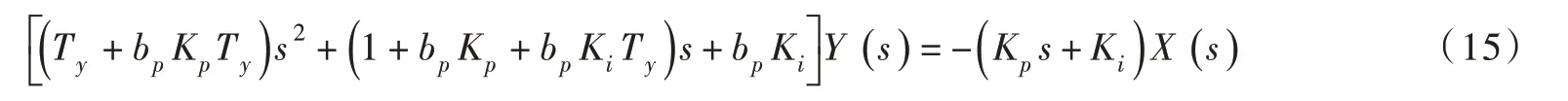
将式（13）和式（14）代入式（15），整理得：

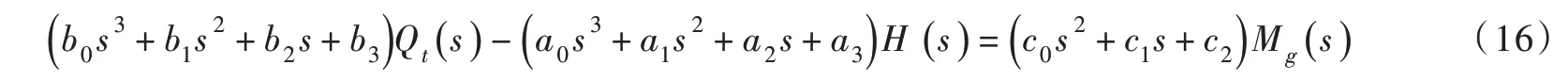
式中：a0=λ6λ1；a1=λ6λ2+λ5λ1；a2=λ6λ3+λ5λ2-Kpλ4；a3=λ5λ3-Kiλ4；b0=Taλ1；b1=Taλ2+enλ1；b2=Taλ3+enλ2+Kpey；b3=enλ3+Kiey；c0=-λ1eqx；c1=-(λ2eqx-Kpeqy)；c2=Kieqy-eqxλ3；λ1=λ2eqx-Kpeqy；c2=Kieqy-eqxλ3；λ1=Ty+ bpKpTy；λ2=1+bpKp+bpKiTy；λ3=bpKi；λ4=eqyeh-eqhey；λ5=eqhen+eqxeh；λ6=eqhTa。

式（16）可改写为：

式中： B=b0s3+b1s2+b2s+b3；A=a0s3+a1s2+a2s+a3；C=c0s2+c1s+c2

式中：QT为水轮机处复流量，m3/s；HT为水轮机处复水头，m；ΔMg为发电机负载力矩变化量，N·m；Mg0为初始工况发电机负载力矩，N·m。

水轮机前后管道的复水头HT和复流量QT之间满足如下关系［14］：

若考虑水轮机前后管道的水体动能，式（19）可改写为：

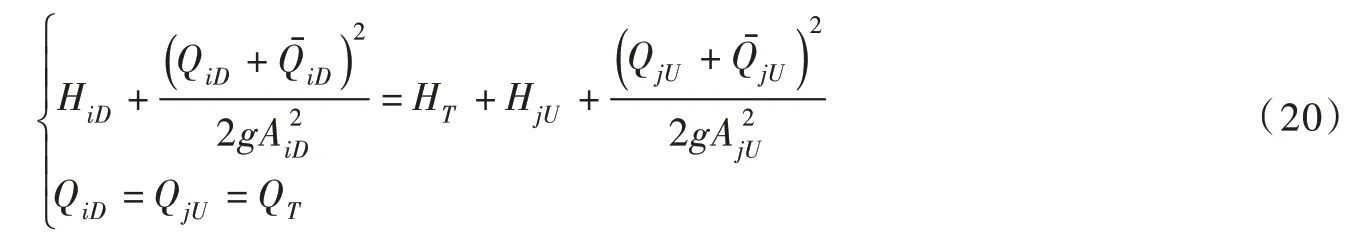
式中：HiD为第i段管道末端复水头，m；HjU为第j段管道首端复水头，m；QiD为第i段管道末端复流量，m3/s；QiU为第i 段管道首端复流量，m3/s；为第i 段末端管道平均流量，m3/s；为第j 段首端管道平均流量，m3/s；AiD为第i 段末端管道面积，m2；AjU为第j 段首端管道面积，m2；

引入恒定流条件并对上式做线性化处理，略去高阶非线性项，上式化简为：

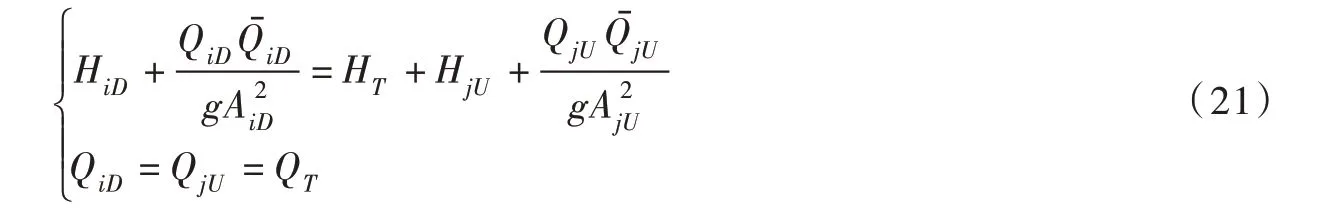
可写成传递矩阵的形式：

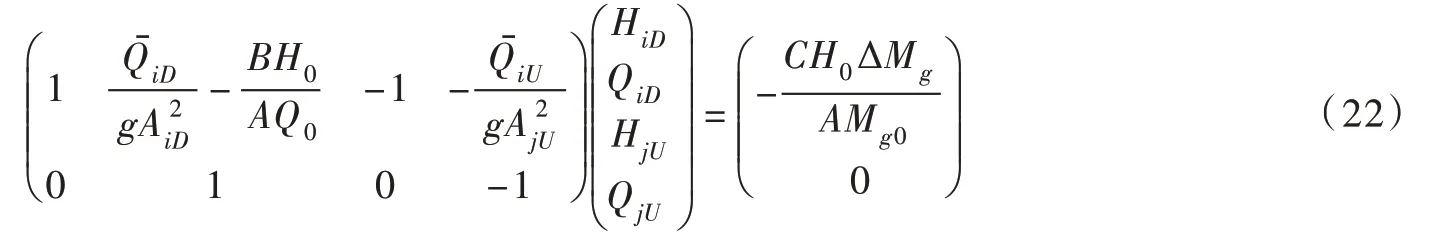
式（22）为完整的机组阻抗通用表达式，针对简单或复杂的有压输水发电系统皆能适用。

2.2 管道及有关边界条件的传递矩阵管道及有关边界的传递矩阵详见参考文献［14］，式（23）—式（27）为本文用到的边界条件。根据管道首末两端复水头和复流量的关系，可写成传递矩阵，如式（23）所示：

式中：li为第i 段管道长度，m；gi为第i 段管道传播常数；ZCi为第i 段管道特征阻抗。

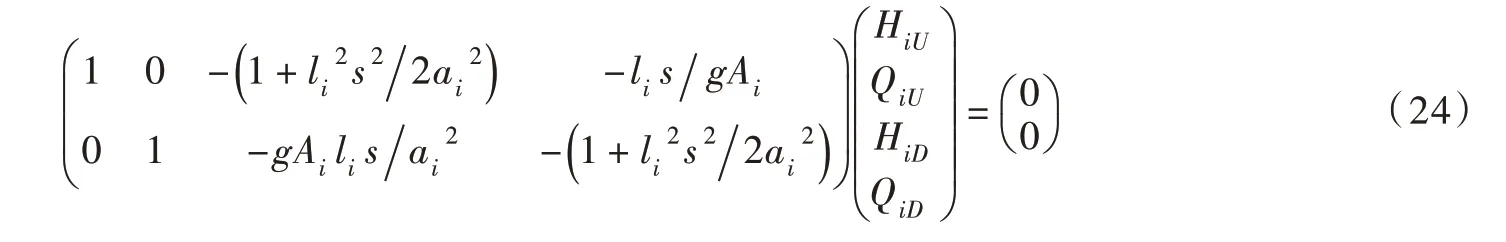
对于单管单机系统，假定过渡过程中上、下游水库水位不变，即H1U=0 和H2D=0，则式（24）可改写成式（5）和式（6）的形式。

根据岔管前后复水头和复流量的关系，可写成传递矩阵的形式，如式（25）所示：

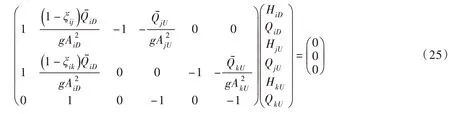
式中：xij第i 段与第j 段管道间局部损失系数；xik第i 段与第k 段管道间局部损失系数。

上游水库边界条件，考虑管道水体动能和局部水头损失的管道首端面复水头和复流量的传递矩阵为：

式中x 局部水头损失系数。

下游水库边界条件，考虑管道水体动能和局部水头损失的管道末端面复水头和复流量的传递矩阵为：

2.3 总体矩阵的构成及稳定性的判据在本文研究中，忽略了系统水头沿程损失和局部损失，调节系统为线性系统，水击模型为二阶水击模型，重点分析调速器参与频率调节时比例增益Kp与积分增益Ki对稳定性的影响。

由管道、岔管和水轮机等传递矩阵可建立输水发电系统总体矩阵U，参数之间关系的方程组为：矩阵B 为边界条件列向量。由于每根管道有4 个未知数，对于n 根管道构成的水力系统总体矩阵U 的大小为4n×4n，前2n 行表示管道传递矩阵，后2n 行表示上库、岔管和水轮机等传递矩阵，矩阵B 大小为4n×1，为首末断面复水头和复流量构成的未知量向量，表达式如下［14］：

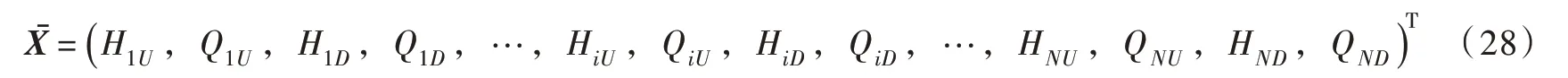
假设系统无外部扰动，即B=0，给定一组调速器参数Kp与Ki，采用牛顿迭代法求出U=0 时对应的频率ω和衰减因子σ。对于总体矩阵，可求得其中最大的衰减因子σmax，当衰减因子σmax＞0 时，系统处于不稳定状态点；当σmax=0 时，即系统处于临界稳定状态点；当σmax＜0 时，即系统处于稳定状态点。进行多次计算后可根据σmax=0 时的调速器参数值求得系统的稳定域。具体计算流程图如图1所示。

3 对比分析

3.1 单管单机系统以梨园水电站为例，用总体矩阵法分析输水发电系统运行稳定性，并与传递函数法和Simulink 仿真结果进行对比。该水电站基本资料：单管单机输水发电系统，无调压室，布置示意图如图2，管道参数如表1。机组额定出力612 MW，额定水头106 m，额定流量621.4 m3/s，额定转速166.7 r/min，管线水流加速时间常数TW=4.02s，机组加速时间常数Ta=9.65s。水轮机传递系数取eh=1.49，ex=-0.99，ey=0.67，eqh=0.5，eqx=0.0，eqy=0.77。其他参数取Ty=0.02s，bp=0.04，eg=0。

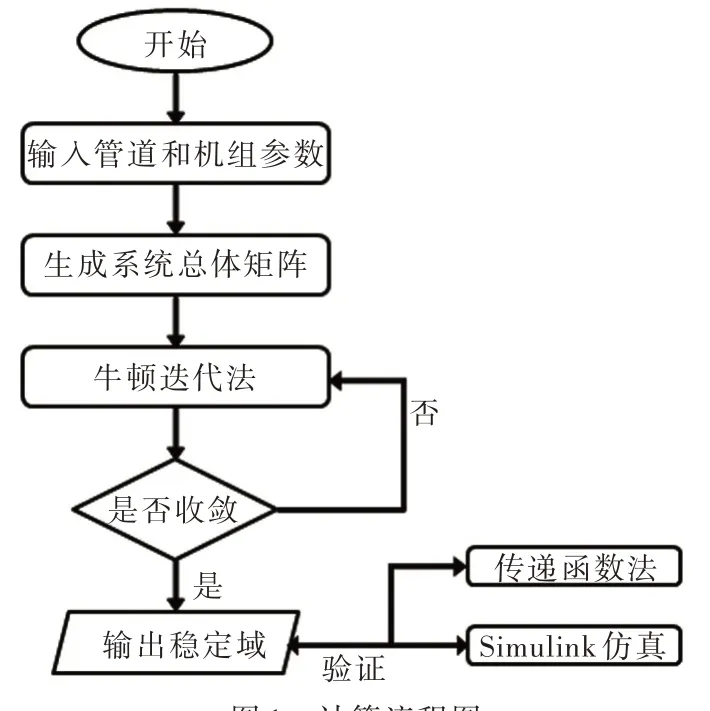
图1 计算流程图

图2 梨园水电站管线示意图

表1 管道参数

图3所示为用总体矩阵法求解不同调速器参数对应的最大衰减因子σmax。通过变换求取σmax=0 时对应的Kp和Ki值，如图4绿色线所示；用传递函数法进行数值模拟，结果如图4蓝色线所示。曲线下半部分为稳定域，上半部分为不稳定域。可以看出，两条线重合。

用Simulink 建立调节系统整体模型，取通过总体矩阵法推导出的稳定域边界上的若干组点，进行数值仿真，可得到稳定点与不稳定点，如图4所示。以两组参数为例：①Kp=1.0，Ki=0.37；②Kp=1.0，Ki=0.39。扰动为阶跃扰动，扰动值为0.1，扰动从第10 s 开始，输出的时域响应如图5和图6所示。当Kp=1.0，Ki=0.37 时，调速器参数处于稳定域内，系统是稳定的，响应曲线收敛。当Kp=1.0，Ki=0.39 时，调速器参数处于不稳定域，系统是不稳定的，响应曲线发散。

上述3 种方法得到的计算结果，高度吻合。说明了总体矩阵法可准确求解单管单机输水发电系统的运行稳定域，为进一步验证总体矩阵法的适用性奠定了基础。

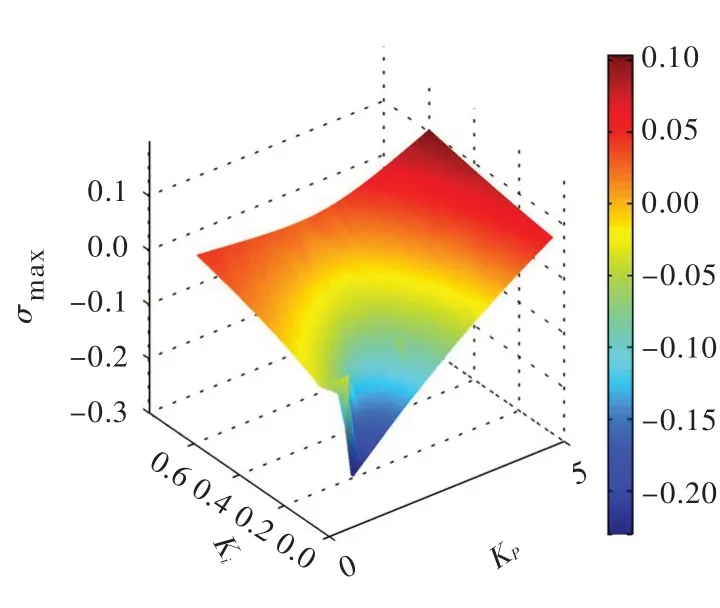
图3 不同调速器参数对应的最大衰减因子σmax（总体矩阵法）

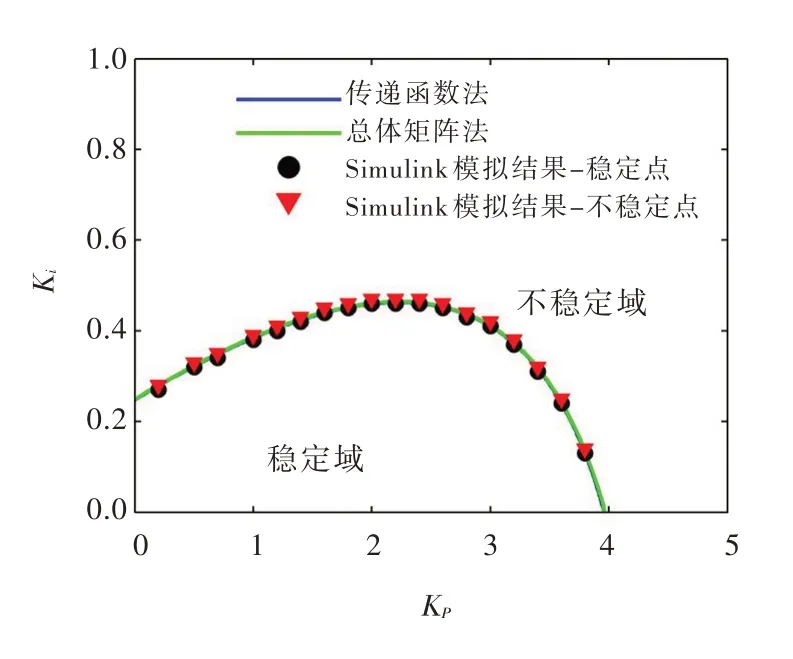
图4 总体矩阵法与传递函数法和Simulink模拟对比

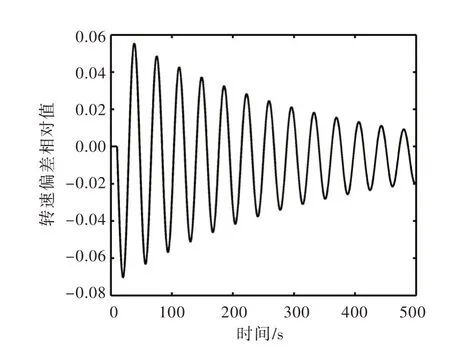
图5 负荷给定扰动阶跃响应（KP=1.0，Ki=0.37）

图6 负荷给定扰动阶跃响应（KP=1.0，Ki=0.39）

3.2 一洞四机系统以喀腊塑克水电站为例，分别用总体矩阵法和Simulink 仿真分析电站稳定性。该水电站基本资料：一洞四机输水系统，布置示意图如图7，管道参数如表2。机组额定出力36 MW，额定水头79.5 m，额定流量50.23 m3/s，额定转速300 r/min，1#管线水流加速时间常数TW=2.98s，机组加速 时 间 常 数Ta=10.11s。 水 轮 机 传 递 系 数 取eh=1.4568， ex=-0.9136， ey=0.6001， eqh=0.5320，eqx=-0.0640，eqy=0.8391。其他参数取Ty=0.02s，bp=0.02，eg=0。

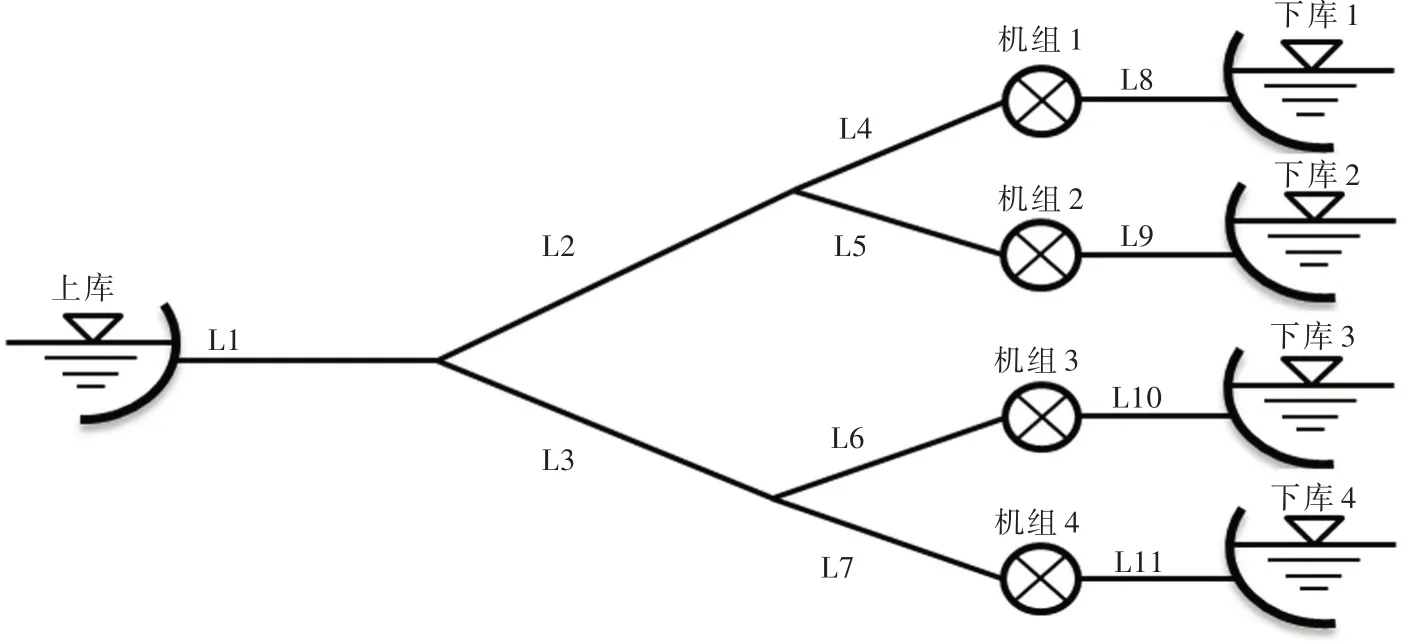
图7 喀腊塑克水电站管线示意图

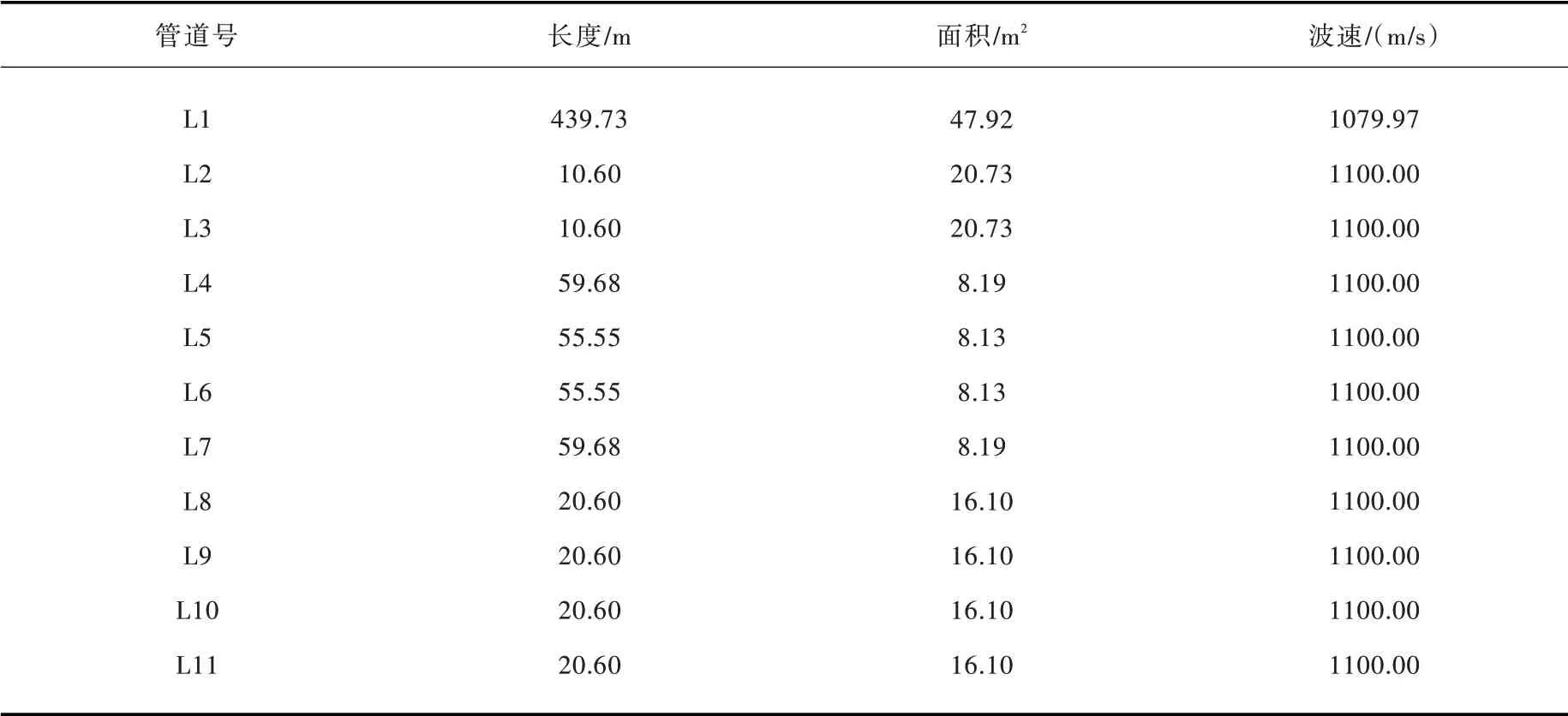
表2 管道参数

图8所示为用总体矩阵法求解不同调速器参数对应的最大衰减因子σmax。通过变换求取σmax=0 时对应的比例增益Kp和积分增益Ki值，如图9绿色线所示，曲线下半部分为稳定域，上半部分为不稳定域。

用Simulink 建立调节系统整体模型，取通过总体矩阵法推导出的稳定域边界上的若干组点，进行数值仿真，可得到稳定点与不稳定点，如图9所示。以两组参数为例：①Kp=3.0，Ki=0.53；②Kp=3.0，Ki=0.55，用Simulink 建立调节系统整体模型，进行仿真模拟。扰动为阶跃扰动，扰动值为0.1，扰动从第10 s 开始，输出的时域响应如图10和图11所示。当Kp=3.0，Ki=0.53时，调速器参数处于稳定域内，系统是稳定的，响应曲线收敛。当Kp=3.0，Ki=0.55 时，调速器参数处于不稳定域，系统是不稳定的，响应曲线发散。两种方法得到的结果完全相同，再次验证了总体矩阵法的准确性，说明了总体矩阵法可以用于一洞四机输水发电系统的运行稳定性分析中。

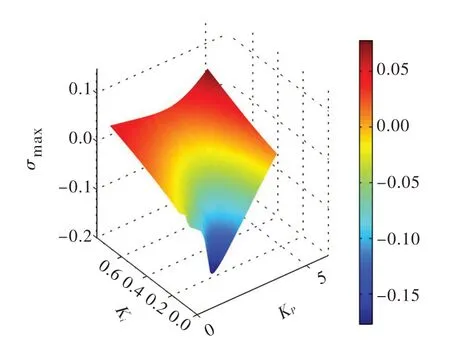
图8 不同调速器参数对应的最大衰减因子σmax（总体矩阵法）

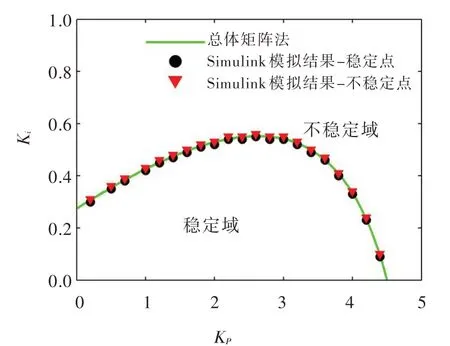
图9 总体矩阵法与Simulink 模拟对比

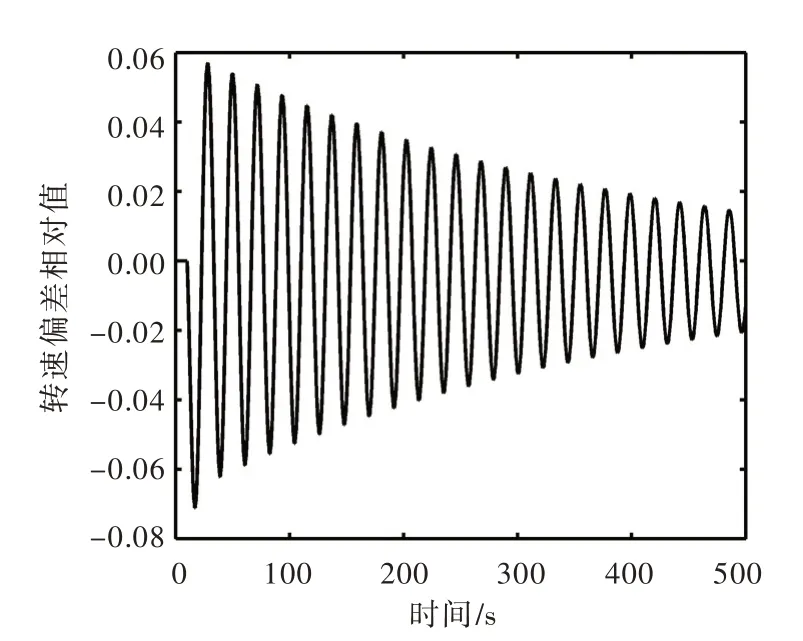
图10 负荷给定扰动阶跃响应（KP=3.0，Ki=0.53）

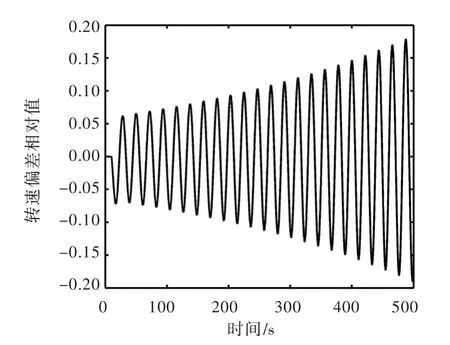
图11 负荷给定扰动阶跃响（KP=3.0，Ki=0.55）

4 结论

本文将总体矩阵法应用于水电站输水发电系统运行稳定性分析中，推导了机组阻抗表达式，建立了布置形式为单管单机和一洞四机的水电站输水发电系统总体矩阵，以最大衰减因子σmax是否小于0 作为稳定性的判别依据，绘制出相应的稳定域。本文还通过上述两个工程实例对本方法进行了验证：（1）用传递函数法和Simulink 仿真对单管单机系统进行了对比验证，结果表明总体矩阵法所得到的稳定域与传递函数法和Simulink 仿真得到的稳定域吻合度较高， 说明了采用总体矩阵法可以计算单管单机的稳定域。（2）建立了管道系统Simulink 模型对一洞四机系统进行验证，结果是总体矩阵法所得到的稳定域与Simulink 仿真得到的稳定域重合，说明了采用总体矩阵法可以计算复杂管道系统的稳定域。当水电站布置形式发生变化时，只需修改系统各个模块相应的传递矩阵排列顺序即可，极大方便了运行稳定性分析，为深入分析各种不同复杂管道系统水电站运行稳定域提供了新的途径。