并联供水水库联合调度规则最优性条件研究Ⅱ：算法开发与实例研究

胡铁松，曾 祥，王 敬，王 欣，汪 琴

（武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072）

1 研究背景

高效求解技术的开发是水库群联合优化调度的核心内容，而利用水库调度问题的特征选择或者开发优化算法不仅有助于挖掘水库蓄放水决策规律，而且有助于提高优化求解效率，是水库优化调度研究的难点与热点问题［1-2］。

作为水库调度问题的基础结构单元，两阶段调度决策问题可以通过水库状态转移方程描述多阶段调度决策问题。因此，国内外针对两阶段调度问题的特征开展了大量研究，设计了不同的高效求解方法。Zhao 等［3］根据供水调度目标的边际效益递减性质构造了搜索域缩减算法和邻域搜索算法，显著提高了动态规划的求解效率；You 等［4］研究了径流不确定性对水库调度决策的影响机理并开发了限制供水决策技术；Zhao 等［5-6］推求了两阶段调度模型的最优性条件，由此设计了单库两阶段及多阶段优化求解方法；Zeng 等［7］揭示了并联供水水库总供水量确定规则的最优性条件，提出了成员水库供水任务分配原则。遗憾的是，上述研究成果仅限于单库调度问题以及特定情境下的并联水库联合调度问题，如何将相关理论与方法拓展到一般性条件下并联供水水库联合调度中，需要解决以下两个问题：（1）提取并联供水水库联合调度问题的一般性最优条件，这是文献［1］解决的问题；（2）利用上述条件改进或开发高效求解技术，这是本文解决的问题。

因此，本文利用文献［1］中并联供水水库两阶段调度问题的K-T 条件，设计该类问题的滚动优化求解方法，根据两阶段调度问题与多阶段调度问题最优策略集具有一致性的假设条件，滚动运行两阶段调度模型，实现并联水库系统长时序优化调度的目的。在辽宁省碧流河水库与英那河水库的实例研究中，通过与现有并联水库联合调度规则的比较，验证新算法的合理性与有效性。

2 并联供水水库两阶段调度问题最优求解技术

由动态最优化理论可知，若多阶段决策问题最优策略集与多个两阶段决策问题最优策略集合具有一致性，则通过两阶段调度模型的滚动运行，逐阶段水库蓄放水最优策略的确定，可以达到系统长时序优化调度的效果［8］。但文献［1］的结论表明，传统的联合调度规则适用条件较差，当且仅当成员水库可利用水量与系统总可利用水量均维持在特定阈值范围内时，并联系统才能达到时段最优供水与分配水效果。因此，为了保障并联系统调度运行的最优性，本文基于文献［1］中并联供水水库两阶段调度模型K-T 条件，借鉴逐步逼近思想，提出并联水库两阶段调度问题的滚动优化求解技术。

该技术以边际成本相等原理作为理论基础，通过逐步满足两阶段模型中的约束条件，调整水库蓄放水策略集，从而达到逼近模型最优解集的目的。

算法首先按照边际成本相等原理对只考虑水量平衡方程条件下的两阶段调度模型进行求解（解析法或者牛顿法），将得到水库群蓄放水策略集带入成员水库自身约束条件修正模块进行更新操作，然后转入总供水量约束检验模块，评估总供水量的可行性，改进成员水库供水策略集，再次转入到水库自身约束修正模块，如此反复，直到所有约束条件得到满足，输出并联供水水库系统蓄放水策略集。算法的具体步骤如下：

（1）步骤1：输入并联水库系统来用水以及水库特征库容等基本资料，给定两阶段调度模型目标函数的表达式以及相关约束条件的边界值；（2）步骤2：按照边际效益相等原理对只考虑水量平衡方程条件下的两阶段调度模型进行求解，确定每个水库时段供水量与时段末蓄水量；（3）步骤3：检验步骤2 输出的成员水库蓄放水决策是否具有可行性。若所有水库供水决策均能满足自身供水量与库容约束条件，则转入步骤4。对于不满足自身约束条件的成员水库供水决策，令起作用约束条件的边界值作为水库最优供水决策，并按照蓄放水边际成本相等原理对余下水库的供水决策进行更新操作，然后转入步骤4；（4）步骤4：评估步骤3 输出的并联水库系统时段总供水量是否具有可行性。若满足系统总供水量的约束条件，则转入步骤5。若不能满足总供水量的限制要求，取相应约束条件的边界值为总供水量最优值，并按照蓄水边际成本相等原理对符合水库自身约束条件的供水决策进行改进操作，然后再次转入步骤3；（5）步骤5：输出满足所有物理约束条件的成员水库蓄放水策略集。

基于并联水库两阶段调度问题K-T 条件的滚动优化算法流程图如图1所示。

3 实例研究

3.1 研究区域概况辽宁省大连市是我国东北地区重要的港口与贸易城市。作为大连市主要的水源地，碧流河水库与英那河水库共同承担城市生活与工业的供水任务，构成并联供水水库系统（如图2所示）。其中，碧流河水库正常库容为71 458.5 万m3，汛期库容为66 520.84 万m3（汛期为7月上旬至9月上旬），死库容为7000 万m3；英那河水库正常库容为23 766.12 万m3，死库容为2208 万m3。如图3所示，碧流河与英那河水库目标蓄水量控制线的设置参阅文献［7］与文献［8］。按照设计要求，大连城市供水的设计保证率为90%，缺水允许破坏深度为10%。

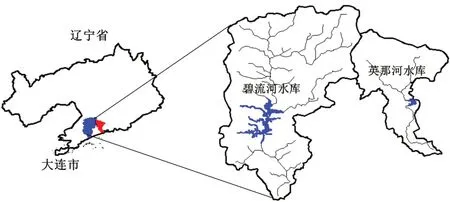
图2 碧流河-英那河并联供水水库系统

3.2 碧-英水库系统联合调度规则及其最优运行区间效益损失函数通常用来描述实际调度结果与理想调度结果的偏离程度，在水库调度研究与实践中被广泛使用。本文采用文献［9］推荐的水库蓄水与供水效益损失函数作为两阶段调度模型的目标函数，其物理意义是使水库时段末蓄水量尽可能地达到理想蓄水状态，并且系统总供水量尽可能地满足用水户需水要求。在并联水库系统长时序调度运行中，该供水效益损失函数的累积和可以反映出用水户的缺水指数（Shortage Index）。效益损失函数的具体数学表达式为：

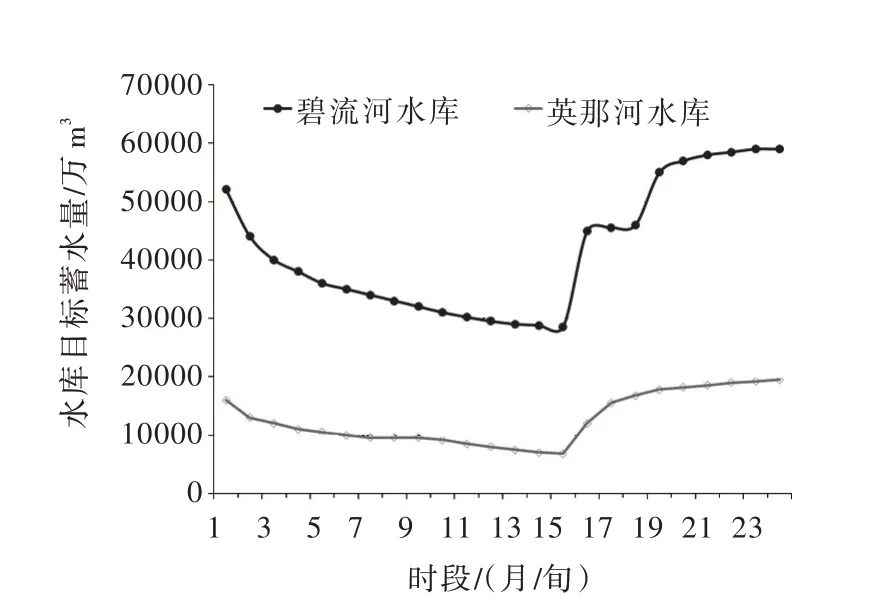
图3 碧流河水库与英那河水库目标蓄水量控制线

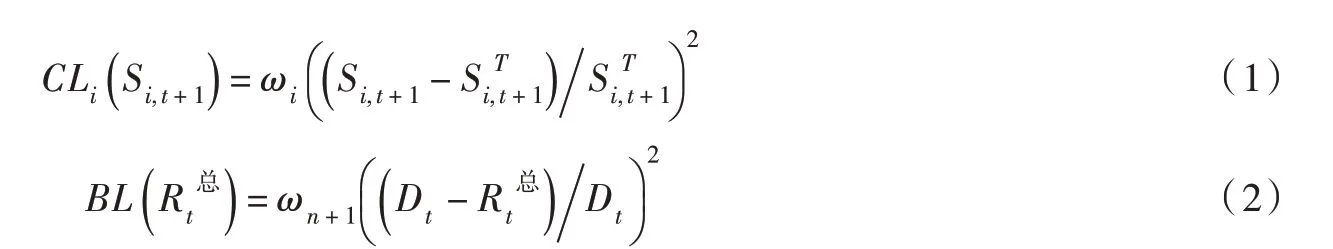
将水库蓄水与供水效益损失函数式（1）与式（2）代入到总供水量确定规则的一般性数学表述形式（文献［1］式（4））中，得到具有解析表达形式的限制供水规则（Hedging rule），即：

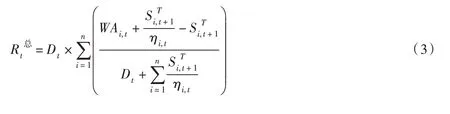
其中：

在此基础上，推得作为蓄水量空间分配规则的参数式规则（Parametric rule）解析表达式如下：

式中： Si,t+1为根据参数式规则确定的第t 时段末第i 个成员水库蓄水量。

由文献［1］提出的可利用水量变化阈值范围可知，满足并联水库联合调度规则最优性条件的系统与水库可利用水量阈值范围分别为：

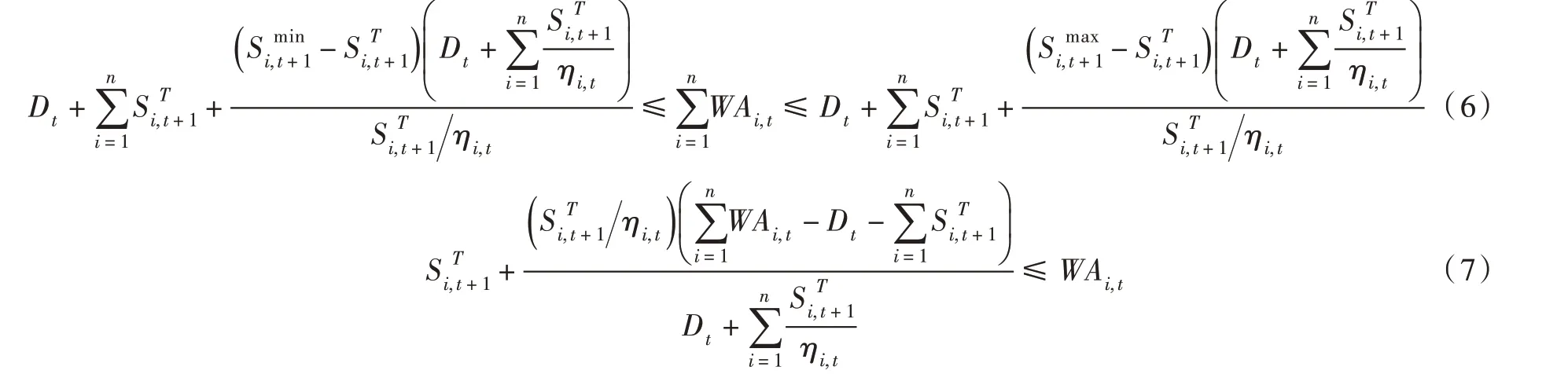
特别地，当效益损失函数的权重系数取值如下式时，水库蓄放水初始边际成本相等（ηi,t=1）

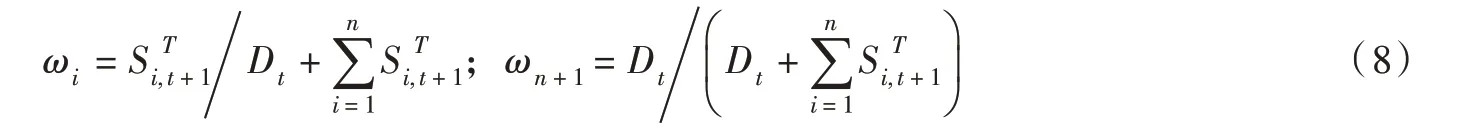
此时，水库蓄放水优先次序由水库库容大小，调节性能高低以及蒸发能力强弱综合确定［1］。

3.3 碧-英水库系统蓄水权重系数的敏感性分析在蓄水权重系数ωi对碧-英水库系统联合优化调度结果的敏感性研究中，将一个水文年度划分为24 个调度时段（4—9月份以旬，其余月份以月作为计算时段），按照滚动优化求解算法与由限制供水规则与参数式规则组合构成的并联水库联合调度规则，设置两种调度方案（其中，方案1 使用新算法求解两阶段调度模型，方案2 采用联合调度规则指导碧-英水库系统的调度运行），分别模拟不同权重系数组合下碧-英水库系统53年（1951—2003年）的长时序调度过程，得到用水户缺水指数与供水保证率的等值线图，如图4—图5所示。

从图4—图5蓄水权重系数组合构成的可行区域可以看出：（1）为了满足用水户最低需水要求，碧流河水库与英那河水库的蓄水权重系数之和不应低于0.70，或者高于0.95。其中，碧流河水库权重系数的取值应当限制在0.35 ～0.80 之间，英那河水库权重系数的取值范围为0.15 ～0.60，并且随着英那河权重系数的增大，可行区间逐渐缩小；（2）当蓄水权重系数的取值均趋近于零时，标准供水策略（Standard Operation Policy，SOP）作为确定碧-英水库系统总供水量的供水规则，不能在碧-英水库系统长时序调度过程中始终满足用水户最低需水要求。这是因为SOP 采用优先满足面临时段需水量的供水方式，导致水库蓄水量不足，未来时段用水户发生超过破坏深度的灾难性缺水事件。因此，SOP 作为并联水库系统的总供水量确定规则，不能保障用水户的最低供水量要求。

从图4（c）与图5（c）中两种方案供水指标的比较可以看出：（1）方案1 在缺水指数和供水保证率这两项指标方面始终较方案2 优越；（2）特别是关于供水保证率方面，方案2 中碧-英水库系统向用水户供水的保证率始终低于90 %，不能达到设计供水要求。因此，由限制供水规则与参数式规则构成的并联水库联合调度规则难以保障碧-英水库系统长时序供水调度的安全运行。

鉴于不同权重系数组合反映出水库蓄放水效益损失函数不同的设置方式，图4—图5的结果在一定程度上表明在并联水库系统调度目标不同的设置方式下新算法具有有效性。

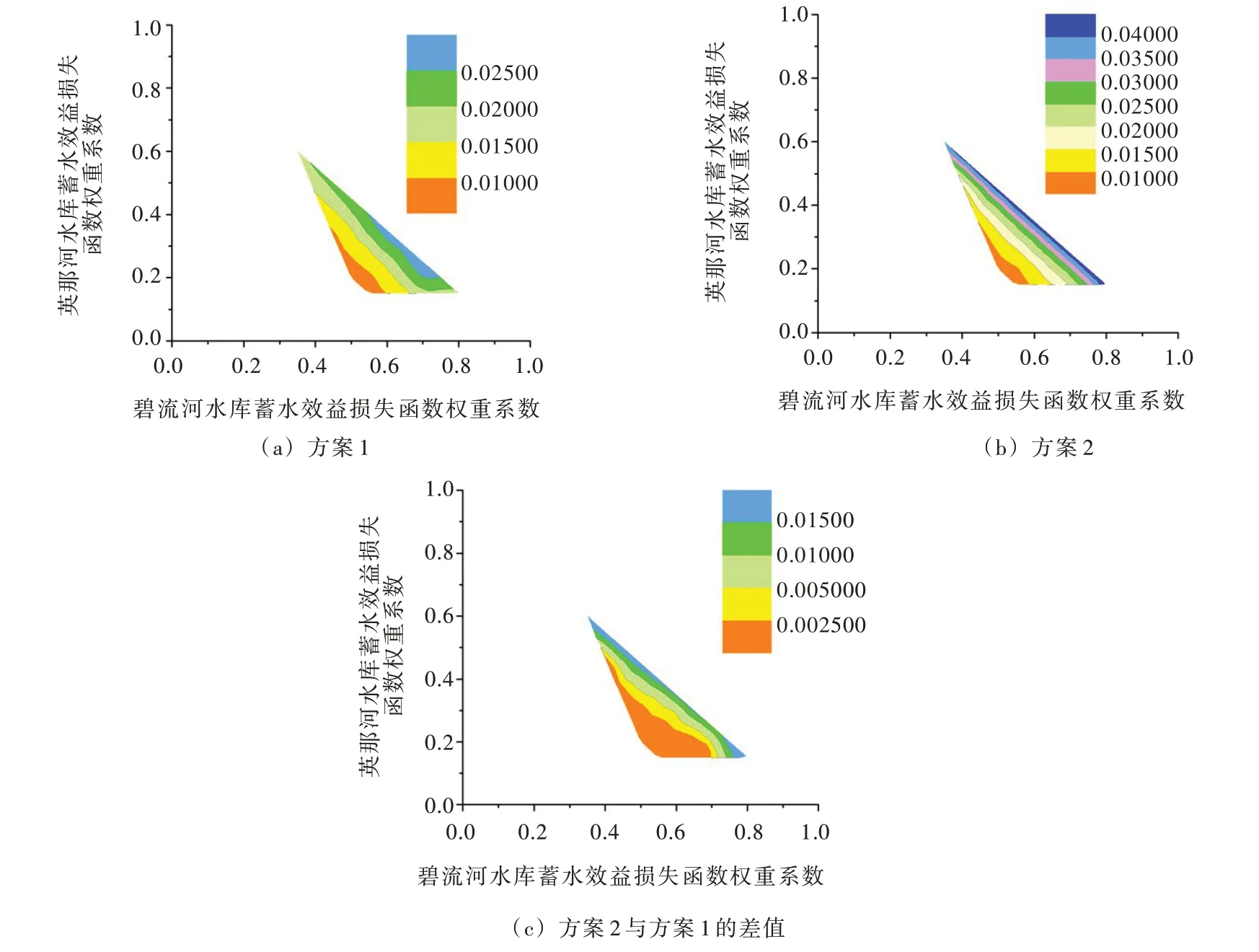
图4 不同权重系数组合下用水户缺水系数的等值线图

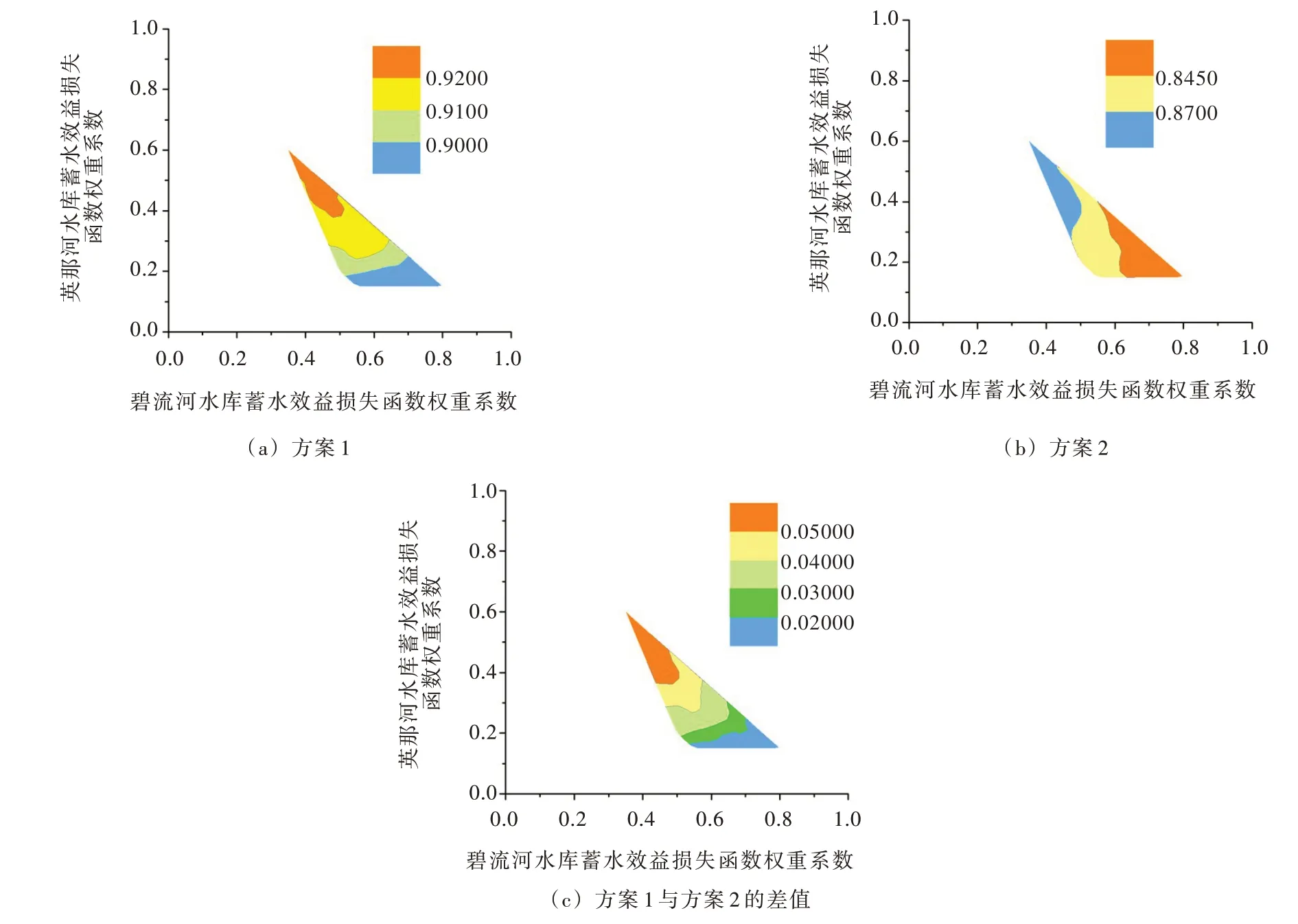
图5 不同权重系数组合下用水户供水保证率的等值线图

3.4 两种调度方案的结果比较与分析方案1 供水效果优于方案2 的现象可以从表1中碧流河水库与英那河水库蓄水权重系数分别赋值0.67 与0.23 时，两种方案在用水户处于缺水状态下碧-英水库系统理想供水量的联合分布得到具体解释（本文将系统总供水量确定之前的成员水库供水量定义为理想供水量，比如算法步骤2 得到的结果）。对比方案2，方案1 有效减少了47 次缺水事件的发生，并且不会出现某一水库理想供水量高于目标需水量而另一水库理想供水量低于非负供水量限制要求的现象。这是因为在新算法中，成员水库非负供水量约束条件会在确定系统总供水量之前进行考虑，通过这种方式系统总供水量的确定综合考虑了水库群总可利用水量与未发生供水行为水库可利用水量的状态，以达到时段最优供水效果。而仅仅依据系统总可利用水量确定水库群总供水量的限制供水规则未能考虑水库自身供水量的约束作用，其结果是将违反非负约束要求的供水决策代入到总供水量的计算过程中，从而导致系统总供水量不能满足需水要求，因此，方案2 缺水事件发生的频次高于方案1。上述分析一方面表明了新算法适用于成员水库与并联水库系统处于较低可利用水量状态的情景（即式（6）与式（7）中水库供水量与蓄水量约束难以得到满足时），另一方面揭示了联合调度规则用于指导系统中存在成员水库未发生供水行为时的局限性。

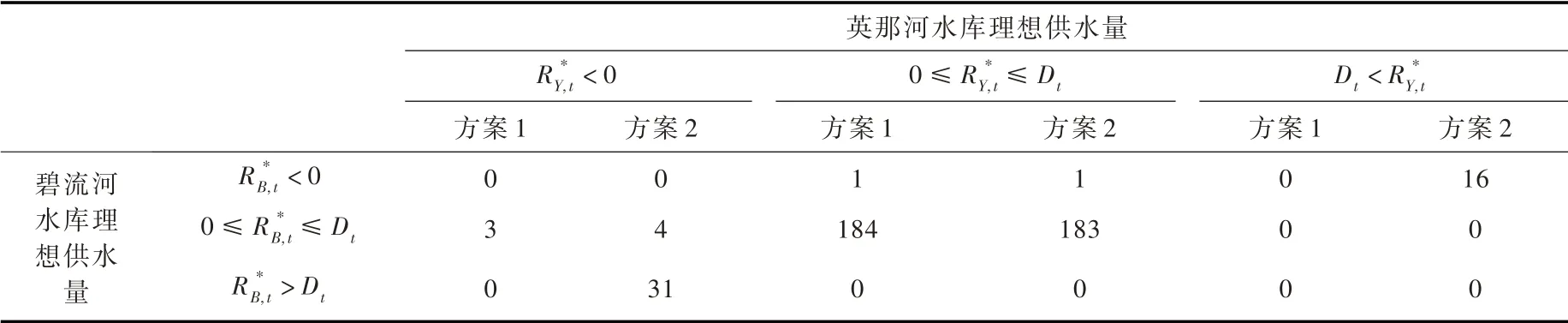
表1 2 种方案中用水户缺水状态系下碧-英水库系统理想供水量的联合分布

3.5 碧-英水库系统蓄放水次序由文献［1］提出的并联水库蓄放水次序划分标准可知，当水库蓄水与供水的初始边际成本均相等时，水库蓄放水次序由水库库容、水库调节性能与库容蒸发比综合确定。图6—图8分别给出了此种情景下碧-英水库系统向用水户供水行为对上述3 种指标变化的响应。

由图6—图8可知：（1）随着水库兴利库容的扩大，入库径流量的增加与水库蒸散发能力减弱，水库向用水户单独供水的行为越频繁，同时另一水库单独供水行为发生的频率也越低。（2）3 种指标对碧-英水库系统供水行为的影响从强到弱依次为：水库库容、入库径流与水库蒸发能力，其中由于蒸发量远小于水库蓄水量与入库径流量，因此，其影响效果并不显著。（3）基于现有碧-英水库工程规模，并联系统应当以碧流河水库与英那河水库向用水户同时供水的方式为主；当碧流河水库库容扩增至现有规模1.5 倍以上时，碧流河水库应当作为补偿水库优先供水；当英那河水库库容扩增至现有规模1.8 倍以上时，碧-英水库系统供水任务主要由英那河水库承担。

图6—图8的结果表明，依据库容大小判定碧-英水库系统的蓄放水次序具有一定合理性，并且在现有供水工程规模下，并联水库系统应当以碧流河水库与英那河水库向用水户同时供水的方式为主。

4 结论

本文以并联供水水库两阶段调度模型K-T 条件作为研究基础，开发了并联供水水库两阶段调度问题的滚动优化求解算法，通过两阶段调度模型的滚动运行，实现了并联水库系统长时序优化调度运行的目的。在碧-英水库系统向大连市联合供水调度的实例研究中，取得了如下结论：（1）新算法在缺水指数和供水保证率这两项指标方面较由限制供水规则与参数式规则组合构成的并联水库联合调度规则优越，主要原因是在新算法中，成员水库非负供水量的约束条件会在确定系统总供水量之前进行考虑，这样系统总供水量的确定综合参照了水库群总可利用水量与未发生供水行为水库可利用水量的状态，达到了时段最优供水效果。（2）相比并联水库联合调度规则，新算法更加适用于成员水库与并联水库系统处于较低可利用水量状态的情景。（3）依据成员水库库容大小判定碧-英水库系统的蓄放水次序具有一定合理性。当碧流河水库库容扩增至现有规模1.5 倍以上时，碧流河水库应当作为补偿水库优先供水；当英那河水库库容扩增至现有规模1.8 倍以上时，碧-英水库系统供水任务主要由英那河水库承担；但在现有供水工程规模下，并联水库系统应当以碧流河水库与英那河水库向用水户同时供水的方式为主。

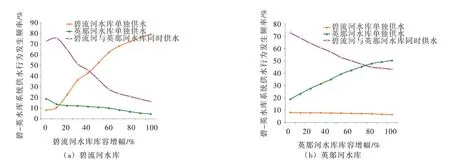
图6 碧-英水库系统供水行为对成员水库库容变化的响应

图7 碧-英水库系统供水行为对成员水库入库径流变化的响应

图8 碧-英水库系统供水行为对成员水库蒸发能力变化的响应