河道糙率和桥墩壅水对宽浅河道行洪能力影响的研究

王 涛，郭新蕾，李甲振，郭永鑫，周志刚，郭晓明

（1. 中国水利水电科学研究院 流域水循环与调控国家重点实验室，北京 100038；2. 珲春市水利勘测设计队，吉林 珲春 133300；3. 黄河水利科学研究院，河南 郑州 450003）

1 研究背景

随着城市化进程加快，天然河流向城市化河流转变过程中，城市内不透水面积增加，改变了径流规律，增加了地表的径流量，同时城市的排水系统也将雨水快速排入河道，导致河道水位涨速加快，洪峰流量增加，加大了城市河道的防洪负担［1］；另一方面城市发展对河道防洪安全保障的需求却在不断提升。河道行洪能力的正确评估是确保安全行洪的基础，在我国北方平原区的河道，一般都具有宽、浅和坡度较缓的特点，其水力学特性复杂［2］。在河道行洪能力研究中，存在许多水力学和河流动力学问题亟待解决。其中，河道糙率是反映河流阻力的综合性系数，也是衡量河流能量损失大小的特征值。北方平原区的宽浅型河流，桥梁的长度一般不会横跨全部泛滥区，穿过河滩的路堤通常压缩了部分汛期过流断面，桥墩的存在占用河道断面，导致洪水下泄时造成水面的壅高对河道行洪能力影响较大［3-4］。

河道多为复杂的复式断面，糙率一般由河道各种糙率单元综合组成，河道植被变化、河床和滩地的材料等不同都影响糙率的选取，正确、合理的糙率选取是河道行洪和输水能力正确评估的关键。刘沛清［5］推导出规则断面的复式渠道输水能力计算公式，提高了计算的精度。Kouwen 和Alfred［6-7］在大量试验和研究的基础上，给出了天然河道不同材料的河床及不同植被的边坡的糙率系数。Nepf和Curran［8-9］研究了天然河床植被变化对河道水力特性的影响，探讨不同生长期植被糙率的变化特性。学者们针对河道和人工渠道糙率通过模型试验［10-11］和数值计算方法［12-13］做了研究和探讨，特别是针对人工输水混凝土渠道和PCCP 管道给出了较为可靠的糙率值［14-15］。天然河道河床滩地植被条件复杂，城市河流人工边坡衬砌材料和形式在不断创新，很难得到较为统一的糙率值满足不同河道需要，特定河道可靠的糙率值通常需要实测资料的率定和模型试验的模拟［16-18］。

在桥墩壅水研究中，壅水高度的确定主要有3 种方法：经验公式法，模型试验法和数值计算［19］。经验公式方法简单便捷，但只能用以粗略求解桥前壅水值以及壅水影响范围，对于复杂的河道和桥梁问题，不同公式用在不同桥梁中计算偏差较大［20-21］，一维河道行洪计算中，桥墩壅水的计算也采用了经验公式进行了简化，二维数学模型能够相对准确的模拟桥墩壅水情况，但因程序设计和边界条件复杂，导致其发展缓慢［22］。在现阶段，物理模型能直观地模拟墩前壅水和河道流态，得到可靠的模拟数据，但成果推广受到经验性限制。

本文以吉林省珲春河珲春市区改造河段为研究对象，探讨宽浅河道影响其行洪能力的关键参数。珲春河发源于汪清县复兴镇杜荒子屯西南秃头岭，自东北向西南流经珲春市，是图们江下游最大的支流。但珲春河防洪工程基本是1960—1970年代为保护两岸农民和农田修建的。年久失修，防洪标准低，不能满足日益发展的城市化和推行国家“一带一路”倡议的需求，因此需要对河堤进行重新规划和修建。新的河堤规划主要在珲春市城区上下游区域，如图1所示。本文以包括珲春大桥和新民大桥在内的城区河段为研究对象，通过物理模型试验和数值计算找到不同植被条件下河道糙率对宽浅河道行洪能力的影响；采用物理模型试验、经验公式和数值模拟方法模拟对比两座大桥壅水的高度，找到河道行洪能力计算中桥墩壅水的可靠计算方法。

2 数学模型和物理模型

本研究河段数值模拟采用一维和二维数学模型，河床糙率研究和桥墩阻力特性研究均采用物理模型试验、经验公式和数值计算方法进行对比。

2.1 数学模型一维恒定流水面线主要通过求解圣维南方程得到。复杂复式河道断面之间的水头损失包括沿程水头损失和局部水头损失，表达式为（Sharp，1981）［23］：

式中： he为水头损失；V1，V1为断面平均流速；α1，α2为动能修正系数；g 为重力加速度；L 为断面平均距离；Sf为两断面间沿程水头损失坡度；C 为收缩或扩散损失系数。断面平均距离表达式如下：

式中： Llob，Lch，Lrob分别是两断面间左边滩地、主槽、右边滩地的距离；Qlob，Qch，Qrob分别是左边滩地、主槽、右边滩地平均流量。

二维水动力学模型建立在连续方程和动量方程基础上采用MIKE 21 建模得到，方程组按交替方向在交错网格上的全隐差分格式进行离散，用追赶法进行求解，采用三角形非结构化网格对计算区域进行划分，计算网格在桥墩附近进行局部加密。

2.2 河道的物理模型在进行物理模型试验时，模型设计以重力相似为主，同时满足阻力相似和水流运动相似；根据洪水特性模型采用正态、定床模型。因为珲春河属于宽浅的河道，河道水浅、流速较小，为确保模型模拟的准确性，模型中的水流和原型水流保持流态的相似，在水工模型设计中，明渠水流的下临界雷诺数应取1000。为了将表面张力的影响减到最小，使其不会妨碍表面波的形成，影响流速和压力分布，要求模型表面流速大于0.20 m/s，模型水深应大于2.5 cm。因此，在模型设计中综合考虑上述流动形态相似、表面张力的影响、糙率模拟准则，尽可能减小模型的缩尺影响，在场地许可范围内，综合考虑河道模拟的物理模型比尺为55。

物理模型试验的目的：验证一维、二维模型及经验公式计算的准确性和合理性，确定河道糙率和桥墩阻力对河道行洪能力的影响。本模型模拟范围为珲春河城区整治河段桩号在15+962 ～18+091之间2129 m 的区域，包括两座城区主要的交通大桥：珲春大桥和森林山大桥，以及河道内规划的亲水平台和生态护坡等复杂的地形和地貌。试验河段河道特征及断面测点布置如图2所示，物理模型试验全景如图3所示。

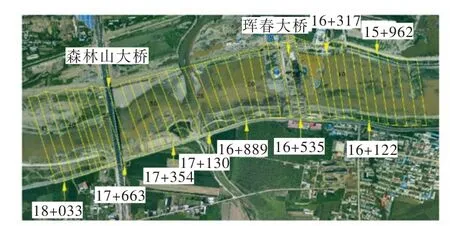
图2 试验河段河道特征

图3 物理模型试验全景

3 河道糙率研究

根据河道规划资料，珲春河河床设计为20年一遇洪水水面线以下主河槽糙率为0.035，该水面线以上为有植被的生态护坡，糙率设计值0.065。在模型比尺为55 条件下，主河槽糙率0.035 对应的模型糙率为0.0179，覆盖植被的生态护坡糙率0.065 对应的模型糙率为0.0333。利用混凝土材料制作的模型，表面抹光的糙率一般在0.010 ～0.011，在混凝土未干结前，利用扫帚等对表面进行打毛，增加模型糙率，但数值一般不超过0.014。为满足糙率相似条件，拟在模型制作时主河槽采用混凝土拉槽方式，两岸生态护坡采用仿真草皮模拟。在模型混凝土表面拉槽进行加糙，当凹槽的尺寸宽0.8 cm、深0.8 cm，模型可达到的糙率为0.019［24］。笔者在其它模型试验中，通过表面刮制宽深0.6 ～0.7 cm 的W 型波纹凹槽进行加糙，实现的糙率值为0.018［25］。天津水运工程研究所给出了拉槽深度、宽度与糙率关系的估算公式［26］，当模型糙率为0.0179 时，初步估算为拉槽宽度和深度为0.7 cm 可满足要求。故本研究模型采用0.7 cm 波浪形凹槽的制作模拟河道糙率，如图4所示。滩地率定综合糙率为0.065，实际河床滩地从生态砖护坡和草皮护坡相结合方式，模型采用草垫加糙，赵海静等［27］利用不同类型的塑料草垫进行加糙，可实现的加糙范围为0.028 ～0.081。笔者在香港锦田河道物理模型试验时，采用不同叶子长度的草垫模拟河道糙率，糙率可达0.031 ～0.036［8］。在本试验中采用如图5所示的密集植被草垫实现滩地综合糙率的模拟，其中草垫叶子密实，叶子长度15 ～20 mm 之间。

图4 原型和模型河床对比

图5 原型和模型河床对比

模型试验中，明渠恒定非均匀流曼宁糙率系数的基本计算方程为：

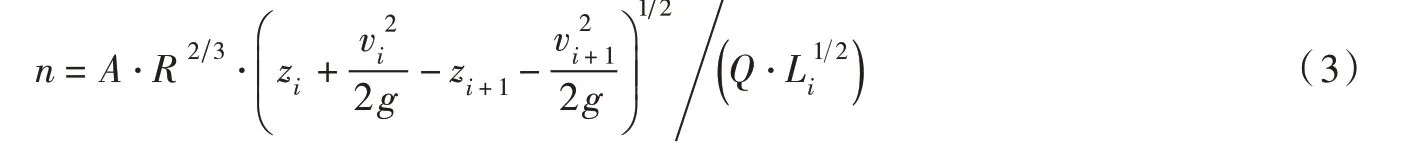
式中：n 为曼宁糙率系数；A 为断面面积，m2；R 为水力半径，m；C 为谢才系数；Q 为流量，m3/s；zi为第i 断面水深，m；vi为第i 断面流速，m/s；其中Li是上、下游断面之间的距离，m。

模型河道各测量段的平均糙率nm可以表述为［20］：

式中：ni为第i 段的糙率；Li为第i 段长度，m；N 是渠道总段数。

国内外学者通过大量的原型观测和试验研究提出了计算综合糙率的经验公式［15］。Pavlovskij（PM）提出的复式河槽综合糙率的表达式为：

式中：Pi为第i 个分割面的湿周，m；ni为第i 个分割面的糙率；P 为整个断面的湿周，m。

Einstein 和Banks（EBM）提出河槽综合糙率计算公式为：

Krishnamurthy 和Christensen（KCM）提出的河槽综合糙率计算公式为：

式中di为第i 个分割面的水深，m。

综合糙率计算结果如表1所示，其中模型率定糙率根据试验实测数据通过式（3）、式（4）计算得到，试验率定结果显示：全河道采用混凝土拉槽后糙率为0.0179，加上生态护坡草皮后原型河道的综合糙率为0.0357。EBM、PM 和KCM 的综合糙率值是根据设计的主河槽糙率为0.035，生态护坡糙率为0.065，分别采用复式断面渠道综合糙率式（5）—式（7）计算得到。从表上可以看出，EBM 和PM 公式计算的河道综合糙率均为0.0371和0.0374，KCM 公式计算的河道综合糙率为0.0356，和试验率定糙率值一致。这是因为虽然PM、EBM 和KCM 公式都是在建立在一定假设基础上推导出的，但同MP 和EBM公式相比，KCM 公式中考虑到各分割面的水深作为影响因子，使得该公式计算结果更接近真实糙率。

在50年一遇洪水（设计流量：3325 m3/s）条件下：模型试验的水面线同二维数值模拟（主河床糙率为0.035，生态护坡糙率为0.065）水面线如图6所示，计算值和模型实测值吻合较好，最大水位误差在0.04 m。表明珲春河设计渠道糙率为0.035，生态护坡糙率为0.065 是符合河道实际情况的。

表1 综合糙率计算结果

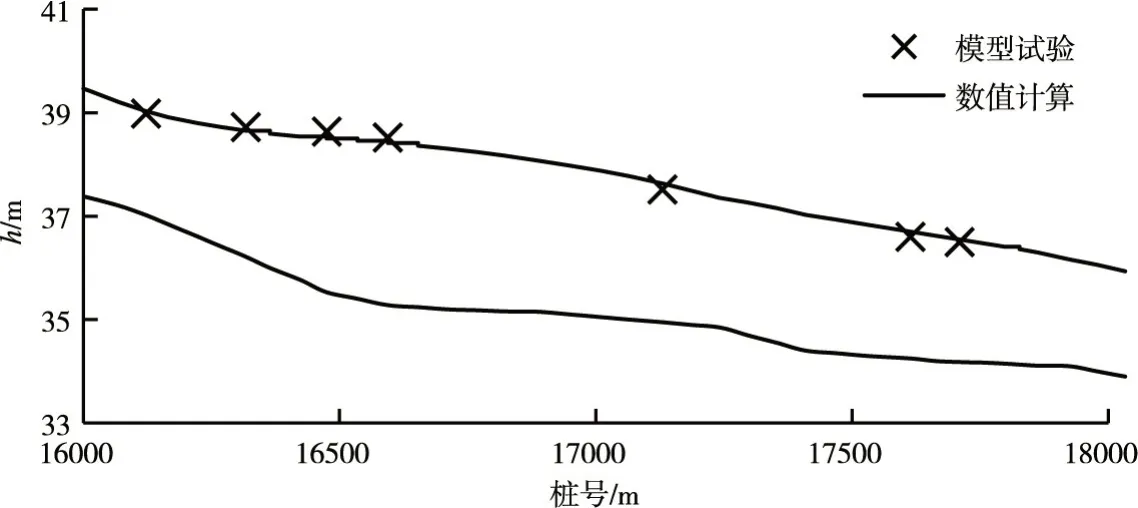
图6 模型试验和数值计算水面线比较

在天然河道中，护坡的植被随着季节和时间会发生变化，影响河床糙率值。试验中进一步改变护坡的草皮如图7和图8所示，研究在宽浅河道中覆盖植被的护坡糙率改变对洪水水位的影响。稀疏植被种植在60 mm×60 mm 的方格边壁和中心，如图7（b）所示，草的长度25～40 mm。图8的草皮是在稀疏草皮中种植灌木，灌木的布置如图8（b）所示，灌木高度45 mm 左右。

图7 模型中护坡上铺设的稀疏草皮

图8 模型中护坡上铺设的草和灌木

在50年一遇洪水条件下，改变生态护坡4 种不同糙率条件，即：无植被（混凝土拉槽护坡）、稀疏植被、稀疏植被中间种植灌木和密集植被，水面线测量结果见表2所示。结果表明：护坡植被覆盖越密，糙率越大，河道水面线越高，最高的密集植被比最低的无植时水位偏高0.06 m，7 个断面平均偏高0.03 m。所以对于珲春河这样的宽浅河道（B/H＞95），护坡（20年一遇洪水水面线以上）糙率所占综合糙率权重较小，4种不同糙率护坡的河道水面线差别不明显，护坡植被变化对河道行洪能力影响不大。

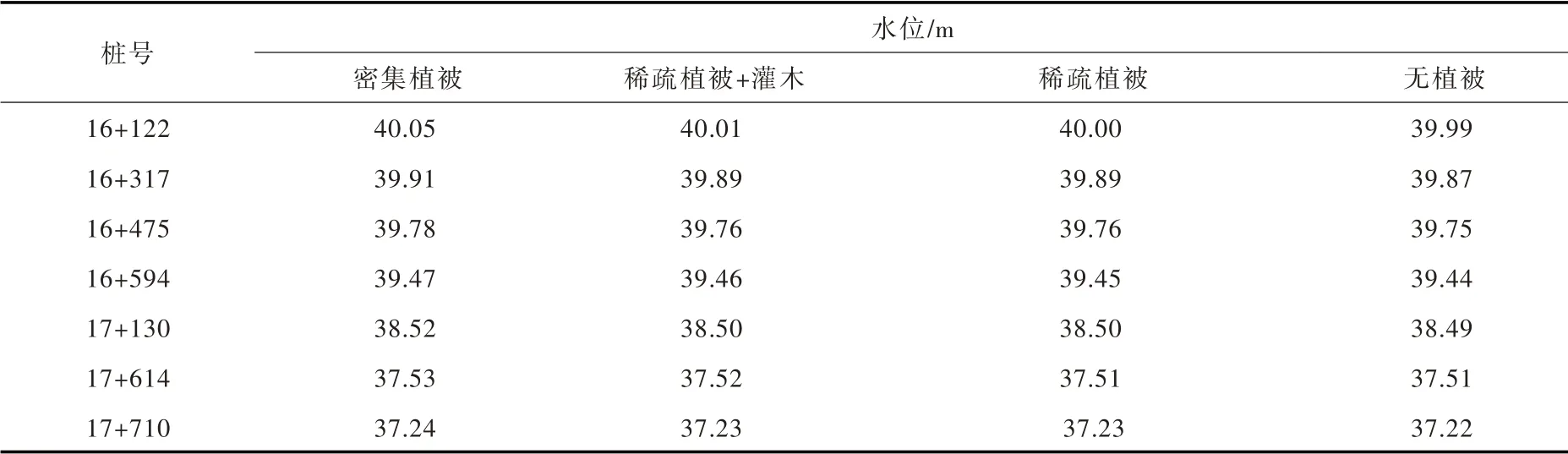
表2 不同植被护坡情况下水位的比较

4 桥墩壅水研究

由于桥墩的存在导致河道的过水断面收缩，桥墩上游水流变缓，水流动能转换为势能，客观表现为水位的壅高，在洪水期间可能会对两岸堤防和桥渡自身安全造成威胁。针对桥墩壅水的计算方法采用经验公式法、数值计算法和模型试验进行比较：模型试验法是按相似准则，利用缩尺模型研究水力学问题的一种手段，能够全面演化复杂边界条件及初始条件下桥墩的水力特性，是研究复杂水力学问题的重要手段；经验公式法是建立在试验和前人研究基础上凝练的公式，常有的有：D’Aubuisson 公式、Yarnell 公式和Yarnell 修正公式等，因其计算过程简单，被广泛的应用在工程中，但经验公式法难以考虑桥墩和河道复杂的条件变化对桥墩壅水的综合影响，也不能揭示桥涵阻水的内在机理，计算结果差别比较大。数值模拟法能快速、便捷的模拟全河道的行洪过程，能够较为全面的反映河道水力特性，提高研究的效率。

位于珲春河上的珲春大桥和森林山大桥是连接珲春河两岸道路运输畅通的重要交通要道，两座桥相距1.2 km，桥墩采用混凝土浇筑，糙率在0.020 左右，要求模型糙率为：0.0097，采用有机玻璃制造能够满足糙率相似。两座大桥桥墩特点如图（9）—（10）模型试验所示，珲春大桥桥长617 m，双幅桥布置，每幅宽27 m，中间有14 m 间隔，主桥布置为独塔双索面混凝土斜拉桥，主河道内主要支撑为中间两组大方形墩子。森林山大桥全长607 m，双幅桥布置，每幅宽17 m，中间5 m 隔离带。均匀分布的圆形桥墩作为支撑，19 排桥墩，每排6 个。不同流量下桥墩壅水试验结果如表3所示，因珲春大桥采用斜拉索结构，主流区只有中间4 个桥墩作为支撑，比森林山大桥减少了对水流的阻力。流量越小，水流主要集中在主河道，滩地过流面积就越小，珲春大桥对水流的阻力作用就越小。

图9 珲春大桥试验模型

图10 森林山大桥试验模型

表3 不同流量下试验测量的水面壅高 （单位：m）

对目前工程中常用的桥梁壅水高度经验计算公式［20］主要有：

D’Aubuisson 公式：

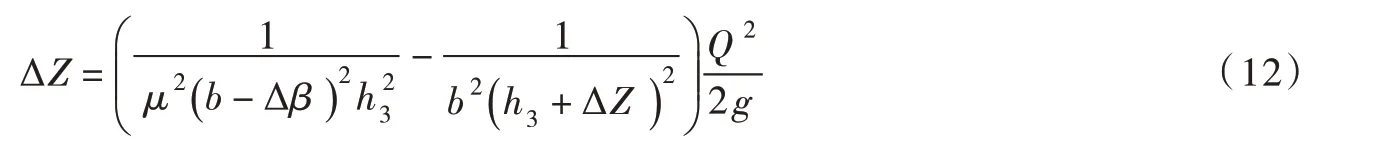
式中：ΔZ 为桥墩水面最大壅高，m；h3为桥后水深，m；μ为同桥墩形状有关的侧收缩系数；b 为渠底宽度，m；Δβ 桥墩总宽度，m。

Yarnell 公式：

式中：k 为试验得到的桥墩形状系数；β 为阻水面积之比，即桥墩淹没部分面积/桥的过水面积；ν3为桥墩下游断面水流流速，m/s；ω=V322gh3，下游断面流速水头与收缩断面下游水深比；h3为下游水深，m。

Charbeneau 和Holleyl 在大量试验的基础上，详细研究了桥墩形状对最大壅水高度和桥墩阻力的影响，修正了Yarnel 公式：

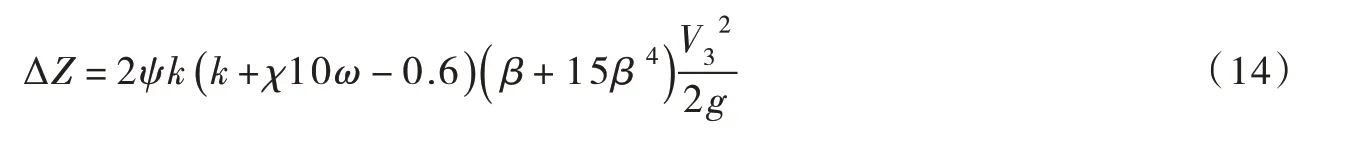
式中ψ、 χ 为桥墩形状修正系数。

在50年一遇（3325 m3/s）洪水工况下，分别采用经验公式、一维和二维数学模型计算桥面最大水面壅高和模型试验结果对比见表4所示。物理模型能客观地模拟墩前壅水和河道流态，得到可靠的模拟数据。三个经验公式中，D’Aubuisson 公式建立在能量平衡基础上得到的，Yarnell 公式和Yarnell 修正公式建立在大量试验基础上。一维模型桥墩阻力的计算和D’Aubuisson 公式的方法一致，因此两者的计算结果相近；珲春大桥桥墩对水流阻力主要来自河道中间1 排4 根的方桥墩，同Yarnell 公式和Yarnell 修正公式试验条件差别较大，因此采用这两个公式计算的珲春大桥水面最大壅高和模型试验数据相比数值较小，偏差较大；Yarnell 公式计算的森林山大桥水面最大壅高较模型试验值偏大，Yarnell 修正公式加入了桥墩形状修正系数，比Yarnell 公式计算的最大壅水高度更接近模型试验数值；二维数值模拟虽然不能完全模拟桥墩的三维特性，但考虑到了到河道的边界条件和水流条件的影响，能够较为直观的模拟桥墩的流场变化，珲春大桥和森林山大桥桥墩最大壅水计算结果均比模型试验结果大0.029 m 和0.059 m。因受场地等客观条件的制约，物理模型不能模拟整个河道的洪水演进，通过同物理模型对比分析，二维数学模型模拟结果同物理模型试验结果较为接近，无论从计算原理、计算方法和试验对比分析，能较真实地反映计算边界、桥梁长度、桥墩形状等对河道水位、壅水高度、流速等水力要素的影响。采用二维数值模型模拟整体河道的行洪能力，都能满足河道安全行洪要求。

表4 50年一遇工况条件下不同模拟方法最大水面壅高的比较 （单位：m）

5 结论

本研究根据宽浅河道特点，研究影响其行洪能力的两个关键参数：河道糙率和桥墩壅水高度。通过物理模型试验、数值模拟和经验公式计算结果比较分析，给出宽浅河道糙率变化对河道行洪能力的影响及河道行洪模拟中桥墩壅水的可靠计算方法。

河道糙率是河道水力计算中的重要因素，关系到河道行洪和输水能力正确评估的关键。本研究提出了物理模型试验中河道不同糙率模拟和率定的方法。通过物理模型试验4 种护坡条件下河道水位变化的比较可知，对于宽浅河道护坡植被随着糙率的明显变化对河道行洪能力影响不显著。

洪水期桥墩的壅水评估不当可能会对两岸堤防和桥渡自身安全造成威胁，本研究通过桥墩壅水模型试验结果同常规经验公式和一维、二维数值模拟结果进行比较，表明经验公式受到使用条件限制，不同公式在同一桥梁中计算结果差别较大，一维数学模型桥墩壅水计算建立在经验公式基础上，也具有一定的经验性。物理模型试验能够全面真实的模拟复杂边界和水流条件下桥墩的壅水情况，二维数学模型考虑到桥墩横向水流特性和相似的边界条件影响，其计算结果同物理模型试验值较为接近，可用于整个河道洪水演进计算。