地震应变率下水饱和度对混凝土动力压缩效应的影响

王海龙，银文文，程旭东，盛余飞，孙晓燕

（1. 浙江大学 建筑工程学院，浙江 杭州 310058；2. 中国石油大学（华东）储运与建筑工程学院，山东 青岛 266580）

1 研究背景

许多情况下混凝土结构不仅要承受静态荷载，还会受到各种动态荷载作用，如地震、各种冲击作用等。动态荷载作用下，混凝土的力学性能与静态荷载作用下的力学性能明显不同，自1917年Abrams［1］注意到混凝土材料的率敏感性以来，许多研究者做了大量的工作。Bischoff 等［2］总结了混凝土动态压缩的试验结果，Malvar 等［3］总结了混凝土动态拉伸的试验结果。但是，目前研究主要集中于应变率较高的冲击荷载范围内，地震应变率范围内的研究成果相对较少，有待深入研究。

桥梁、大坝和港口建筑物等经常在水环境中工作，由于水的浸入，混凝土力学性能会产生一定的改变。关于含水量对混凝土静态力学性能的影响已有较多研究成果，大部分研究发现，静态荷载作用下，含水混凝土的拉、压、弯强度要低于干燥混凝土［4-7］。动态荷载作用下含水量对混凝土力学性能的影响目前也有一些研究，如Yan 等［8］、Suaris 等［9］、Rossi 等［10］发现含水混凝土的动态抗拉强度有显著的增加，而干燥混凝土则不明显；Watstein［11］、Forquin 等［12］、Ranjith 等［13］通过试验发现混凝土抗压强度也有相同的变化规律。但是，Klepaczko 等［14］、Brara 等［15］的研究却发现，在应变率大于1 s-1时，含水量对混凝土的抗拉强度几乎没有影响。虽然含水量对混凝土动态力学性能的影响已有一些研究，但是对含水量影响进行量化探讨的很少，而且现有试验研究所采取的手段多无法规避湿态混凝土进一步水化对其力学性能的干扰影响，这也是导致现有研究结论不太一致的主要原因，因此要厘清含水量这一因素对混凝土动力性能的影响还需要设计专门的试验进行深入研究。本文采用真空饱水设备快速制备不同饱和度的混凝土试件，以消除水泥进一步水化对试验结果的影响，量化混凝土的含水量，揭示不同含水量混凝土在地震应变率下的力学性能变化规律，并通过对比分析不同应变率、不同水饱和度下的混凝土动力效应，探讨水对混凝土性能的影响机理。

2 试验方法

2.1 试件制备制备Φ100 mm×200 mm 的混凝土圆柱体试件进行试验，试验前对试件进行加工磨平，使试件各面垂直，保证试件加载面平整。混凝土配合比如表1所示，粗骨料为连续级配碎石，最大粒径15 mm；细骨料为天然河砂。浇筑24 h 后拆除模具，然后将试件置于标准养护室中养护28 d。

表1 混凝土配合比

所有试件养护完成后，使用电热鼓风干燥箱进行干燥，为避免高温下水分快速蒸发导致混凝土损失，先用50 ℃的温度烘烤1 d，然后逐渐升至65 ℃烘烤3 d，75 ℃烘烤3 d，85 ℃烘烤至混凝土的重量不发生改变为止［16］。为制备不同水饱和度的混凝土，采用混凝土真空饱水机对干燥试件进行快速饱水，以避免普通饱水方法难以充分饱水以及饱水时间过长造成混凝土二次水化。

为了确定混凝土试件水饱和度，试验首先测试获得了试件水饱和度随真空饱水时间变化的经验曲线，具体方法如下：取3 个干燥试件称其质量后放入真空饱水机，每隔一定时间将其取出擦干表面称量其质量，然后再放入饱水机进行饱水，重复此过程直至试件完全饱水，此时其质量不再发生变化。通过式（1）计算混凝土中的含水量，从而获得一系列以饱水时间为横坐标、以水饱和度为纵坐标的数据点，对这些数据点拟合分析得到试件水饱和度随饱水时间变化的经验曲线。根据该曲线，控制混凝土的真空饱水时间就可以得到不同含水量的混凝土。所有试件制备完成后利用塑料薄膜包裹，并在短时间内试验完毕，以防止试件水分蒸发或吸收造成含水量的变化。

式中：wr为混凝土水饱和度，%；mw为饱水状态时混凝土试件的质量，g；mg为干燥状态时混凝土试件的质量，g；m 为水饱和度wr下混凝土试件的质量，g。

2.2 试验设计利用大型液压伺服试验机对不同水饱和度混凝土进行抗压试验，试验机最高工作频率10 Hz，最大施加速度30 mm/s。为了减小试验时端部约束的影响，试件与加载板之间采取聚乙烯塑料薄膜加甘油的减磨措施。试件变形采用标距为100 mm 的引伸仪量测，应力由计算机采集得到。根据图1所示的不同动态荷载所对应的混凝土应变率范围，试验选取应变率分别为1×10-5s-1、1×10-4s-1、1×10-3s-1进行单轴压缩试验。试验采用常应变率加载，通过式（2）计算出恒定应变率下的试件加载速度。每种工况下取3 个试件进行试验，当发现试验数据较为离散时，增加混凝土试件的数量。

图1 不同动态荷载对应的混凝土应变率

3 应变率效应

3.1 应力应变曲线以100%水饱和度混凝土为例，其在不同加载应变率下的应力应变曲线如图2所示。从图2可以看出，随着应变率的增加，应力应变曲线发生了明显的改变。随应变率增加，混凝土试件抗压强度增加，峰值应变减小，另外初始线性段斜率增加，且上升段的非线性部分更小。其它水饱和度混凝土的应力应变曲线也呈现同样的特征。

3.2 抗压强度饱和混凝土抗压强度与应变率的对应关系如图3所示。从图3可以看出，随着应变率的增加，混凝土抗压强度有明显的增长，呈现出单对数线性关系。

混凝土抗压强度表现出的率效应可以用Griffith理论结合亚临界裂纹的扩展进行解释［7］，根据Griffith 理论，当裂纹尺寸超过临界裂纹尺寸时，脆性材料便会发生失效；当加载速度较小时，亚临界裂纹有足够时间去扩展，因此失效发生在应力较小时；当加载速度较大时，亚临界裂纹没有足够的时间去扩展，从而会在应力较大时发生失效。

把应变率为1×10-5s-1时不同水饱和度混凝土的抗压强度看作其静态抗压强度，则动态加载时混凝土的动力强度增长因子DIF 可利用下式进行计算：

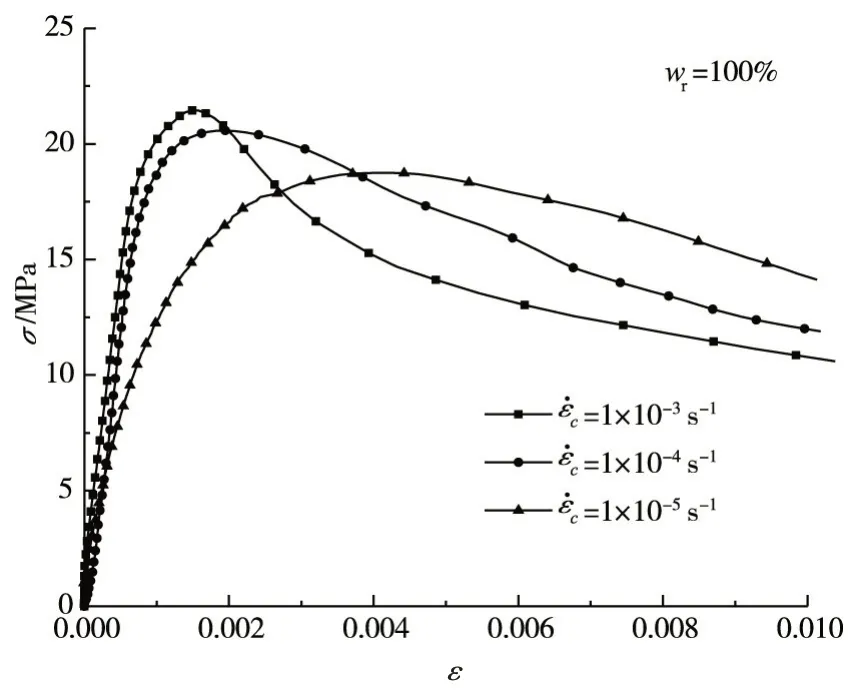
图2 不同应变率下饱和混凝土的应力应变曲线

式中：fc为动态抗压强度；fcs为静态抗压强度。

不同水饱和度混凝土DIF 与应变率的关系如图4所示，其中数据点为3 个试件的均值。从图4可以看出，无论混凝土水饱和度是多少，其DIF 都与应变率的对数值呈线性相关关系，与闫东明等［17］饱和试件的试验研究结果较为吻合。另外可以看出，水饱和度越大，拟合直线斜率越大，即DIF 增长越快，后文将对其影响机理进行详细分析。与干燥混凝土相比，采用本文方法制备的饱和混凝土静态强度下降了40.1 %；而采用自然饱水方法制备的混凝土，文献［18］中其静态强度下降了15.9 %，文献［19］中其静态强度下降了12.6 %，导致这种差异的主要原因可能就是水泥进一步水化导致饱和材料细观结构与对比试件相比发生了较大的变化。

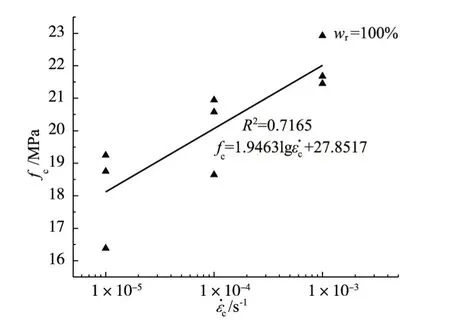
图3 饱和混凝土抗压强度与应变率的关系

图4 不同水饱和度混凝土DIF 与应变率的关系

3.3 峰值应变饱和混凝土的峰值应变与应变率的关系如图5所示。从图5可以看出，随着应变率的增加，混凝土峰值应变减小，其它饱和度混凝土的试验结果也具有同样规律。试验发现，随着应变率的增加，混凝土应力达到峰值时裂纹数量减少。裂纹是影响混凝土变形的重要因素，因此，高应变率下裂缝数量的减少直接导致了混凝土峰值应变的减小。本文试验条件下，混凝土峰值应变与应变率呈图中所示的单对数线性相关关系，其中εc为动态峰值应变， εcs为静态峰值应变。

3.4 弹性模量饱和混凝土弹性模量与应变率的关系如图6所示。从图6可以看出，随着应变率的增加，混凝土的弹性模量增大，其它饱和度混凝土的试验结果也具有同样规律。混凝土弹性模量与应变率之间呈现图中单对数线性相关关系，其中Ec为混凝土动态弹性模量，Ecs为混凝土静态弹性模量。

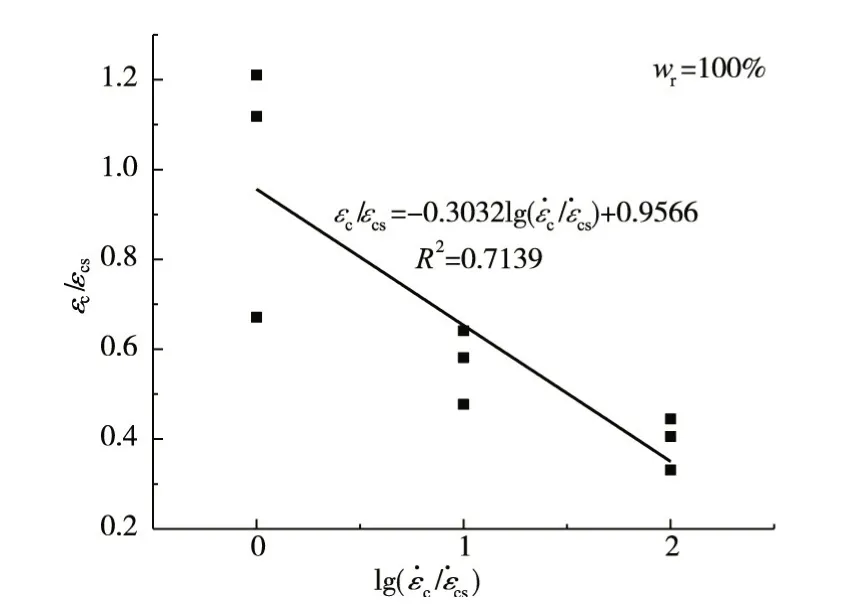
图5 饱和混凝土峰值应变与应变率的关系

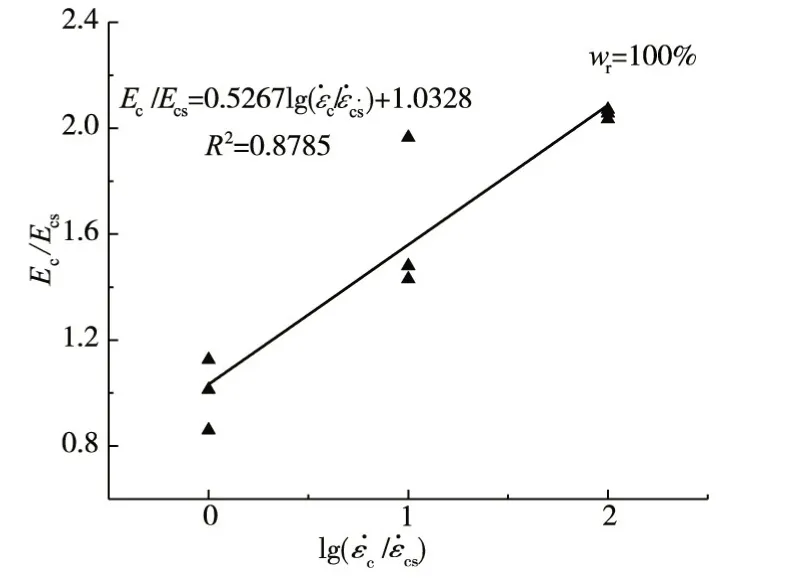
图6 饱和混凝土弹性模量与应变率的关系

4 水饱和度影响

4.1 应力应变曲线不同水饱和度混凝土在动载（=1×10-3s-1）及静载（=1×10-5s-1）作用下的应力应变关系如图7所示。从图7可以看出，与干燥混凝土相比，无论是静载还是动载作用下，随着水饱和度增加，混凝土抗压强度减小。另外，随着水饱和度增加，曲线初始斜率与形状也发生了较大的改变，可见自由水对孔隙的填充增强了混凝土材料的均匀性与密实性。

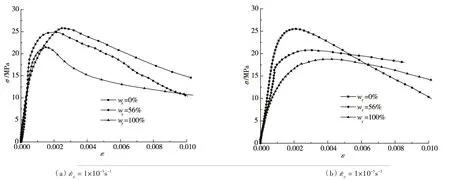
图7 不同水饱和度混凝土的应力应变曲线

4.2 抗压强度混凝土抗压强度与含水量的关系如图8所示。从图8可以看出，无论是静态加载还是动态加载，随着饱和度的增加，混凝土抗压强度减小，二者间呈线性相关关系。混凝土抗压强度的降低可以用表面能的变化来解释，水分的浸入降低了微裂纹成核以及扩展的表面能，从而加速了裂纹的生长［22］。另外，在较低的应变率下自由水可以到达裂纹尖端，其在表面张力的作用下类似于楔体的楔入作用，加速了含水混凝土损伤的发生［23］。

基于混凝土静力试验，Pihlajavaara［24］提出下式用于描述水分浸入对混凝土强度降低的影响：

式中：fw为水饱和度wr时混凝土的强度，MPa；f0为干燥混凝土的强度，MPa；c 为常数；wr为水饱和度，%。

典型的(fwf0)2与水饱和度的关系如图9所示。从图9可见，相关系数达到了0.74，相关程度较高。可见，该关系式不仅适用于静载，在动态荷载下也具有较好的适用性。

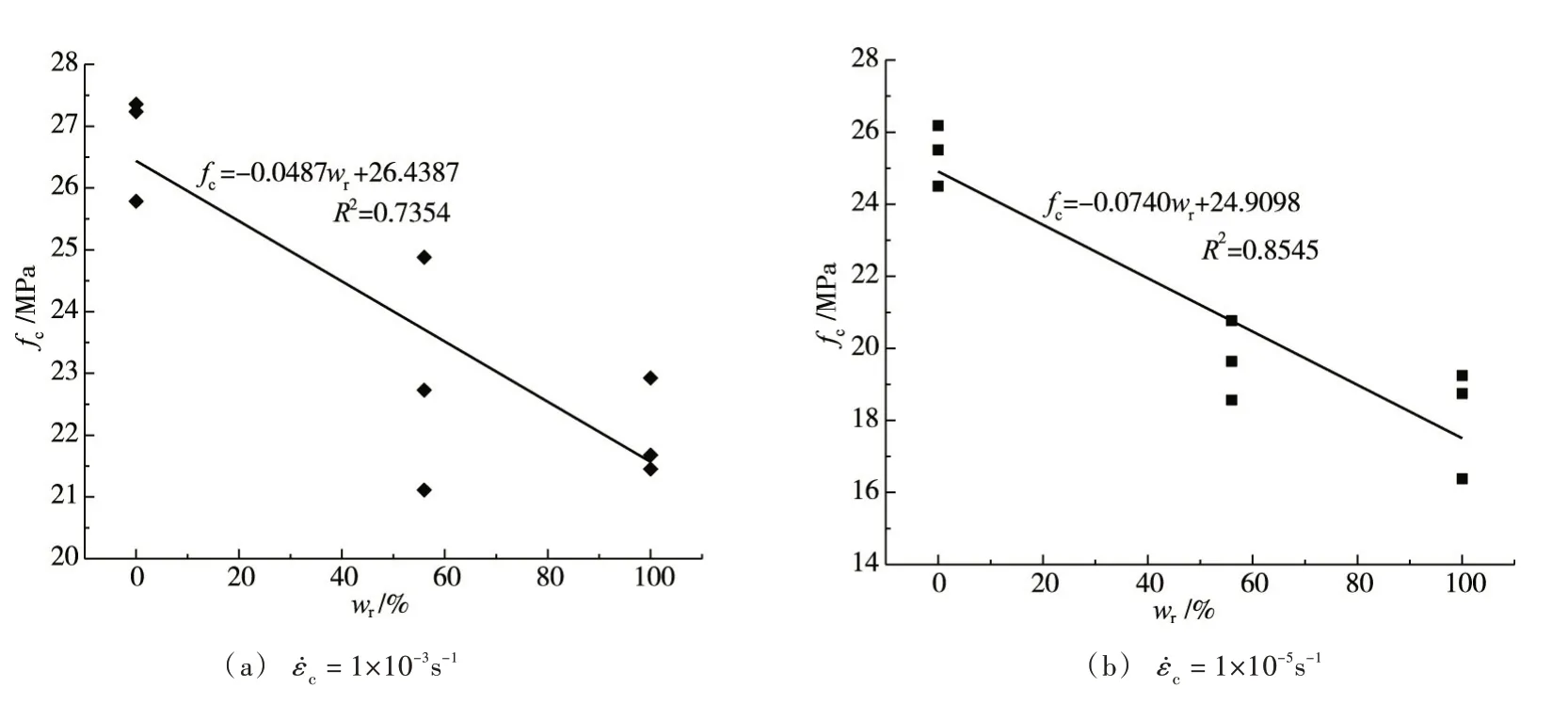
图8 混凝土抗压强度与水饱和度的关系

混凝土动力强度增长因子DIF 与水饱和度的关系如图10所示。从图10可以看出，随着水饱和度的增加，混凝土DIF 有着明显的上升趋势。该趋势说明随着混凝土水饱和度的增加，混凝土率效应增强，其原因可以依据水的黏性效应［25-27］和断裂力学［26］进行解释。压缩荷载作用下，裂纹的扩展包括裂纹面的张开和剪切型错开两种运动形态。裂纹张开时，水的黏性作用可由Stefan 效应揭示，两个距离为h 且半径为r 的圆盘中有黏度为η的液体，圆盘以相对速度v 运动，圆盘间的液体将会对圆盘产生黏性力σv，其大小可由式（5）得到。裂纹发生剪切型滑动时，水的黏性作用可以根据流体的牛顿内摩擦定律求得，即当裂纹以相对速度v 切向运动，根据牛顿内摩擦定律，液体将会对圆盘产生黏性力τv，其表达式见式（6）。当混凝土的微裂纹中存在自由水时，裂纹面的上述相对运动都会产生黏聚力，其大小分别与裂纹的张开与相对错开速度成正比；由断裂力学可知，裂纹扩展速度与荷载的加载速度成正比，因此自由水引起的黏聚力与加载速度正相关。该黏聚力类似于阻止裂纹扩展的阻尼力，因此水饱和度越高对混凝土率效应的影响越强。

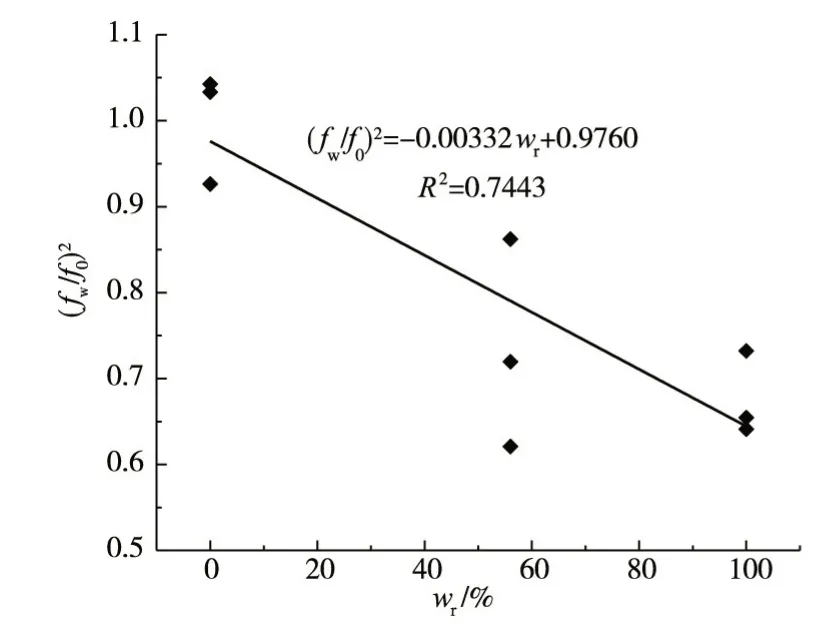
图9 (fw/f0)2与水饱和度的关系（ =1×10-3 s-1）

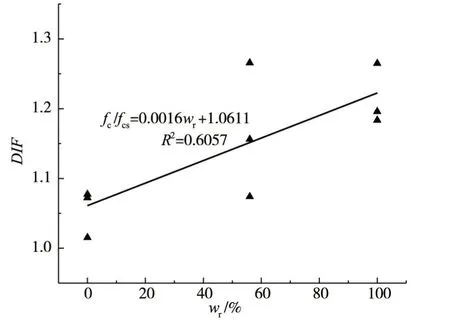
图10 DIF 与水饱和度的关系（ =1×10-3 s-1）

4.3 峰值应变不同应变率下混凝土峰值应变与水饱和度的关系如图11所示，其中数据点取均值。从图11可以看出，在静态加载时，随着水饱和度的增加，混凝土峰值应变增加；在动态加载时，随着水饱和度的增加，混凝土峰值应变有减小的趋势，且应变率越大，减小的趋势越明显。这是因为在应变率较大时，自由水的黏性效应才能发挥出来，延缓了裂纹的扩展，从而降低了混凝土的峰值应变。

4.4 弹性模量混凝土弹性模量与水饱和度的关系如图12所示。从图12可以看出，随着水饱和度的增加，混凝土弹性模量呈现上升趋势，且应变率越高，上升趋势越明显。这是因为混凝土含水量越高，越多的孔隙被自由水充填，混凝土的整体密实性越好、弹性模量越大，而且在动态荷载作用下由于自由水的黏性效应延缓了初始裂纹的起裂与扩展，也导致混凝土刚化［20］。

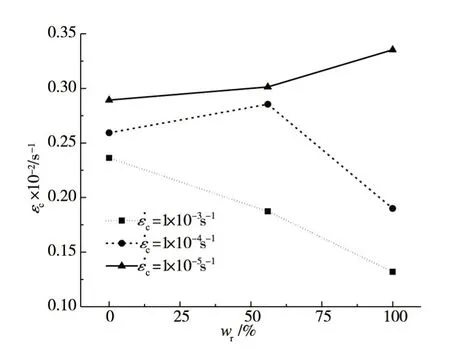
图11 不同应变率下混凝土峰值应变与水饱和度的关系

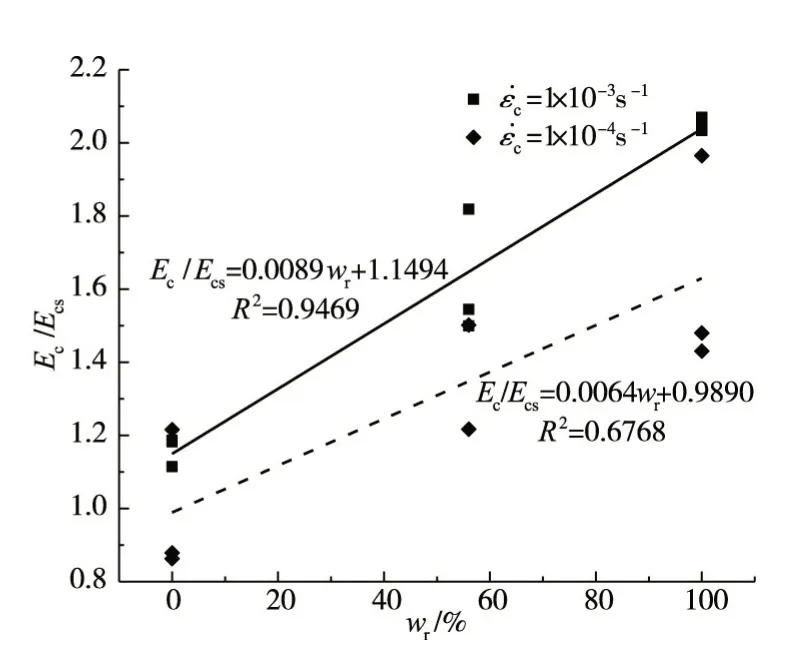
图12 混凝土弹性模量与水饱和度的关系

5 多参数分析

将混凝土水饱和度以及加载应变率看作独立的变量，混凝土动力强度增长因子视作它们的多元函数，结合上文分析可采用如下函数形式进行相关性描述：

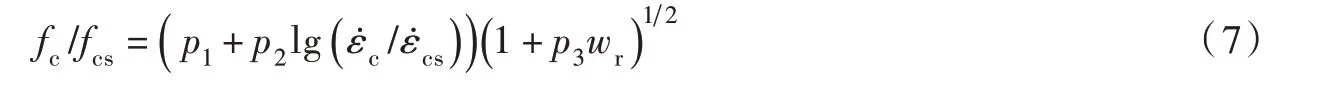
式中：p1、p2、p3均为拟合值。

本文采用MATLAB 软件对试验数据进行拟合，得到p1、p2、p3分别为0.956 5、0.070 41、0.001 757。试验值与计算结果绘于图13，从图13可以看出，虽然试验值和计算值存在一定误差，但总体差距不大，考虑到混凝土动力试验的离散性，该拟合曲线对预测含水混凝土动力强度的增长有一定的参考价值。地震作用下材料的应变率可达1×10-2s-1，根据前文论述本文公式适用的应变率范围可为1×10-6s-1～1×10-2s-1。

混凝土弹性模量采用如下拟合方程：

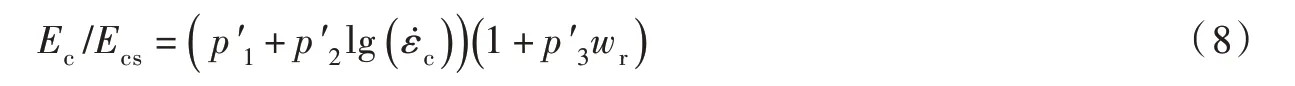
采用MATLAB 软件对试验数据拟合得到p′1、p′2、p′3分别为2.093 7、0.259 8、0.004 9。试验值与计算结果的关系见图14。从图14可以看出，试验值与拟合值整体误差较小，但存在个别数据点误差较大，考虑为离散性或试验误差的原因。

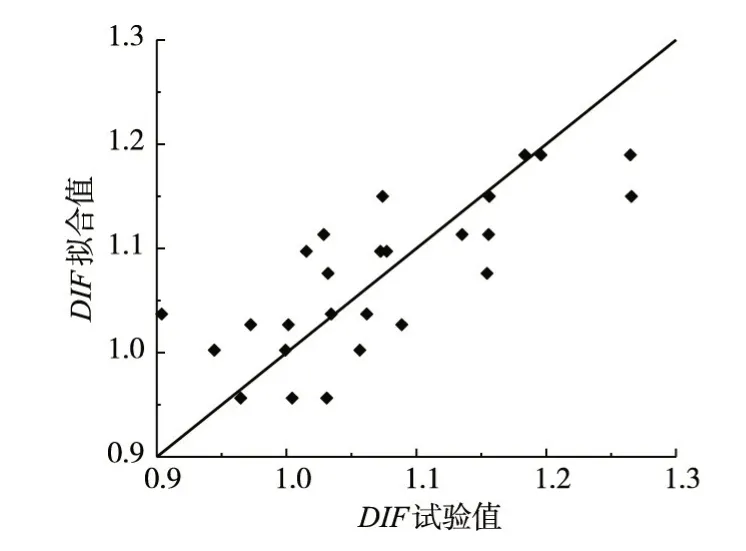
图13 混凝土动力强度增长因子DIF 试验值与拟合值的对比

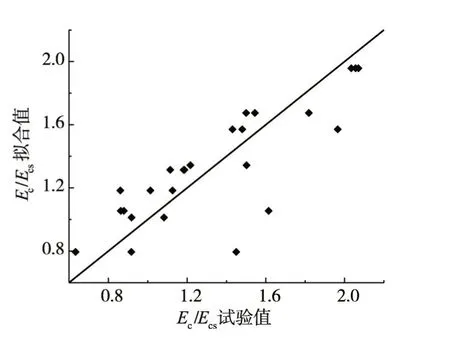
图14 混凝土弹性模量试验值与拟合值的对比

6 结论

本文试验研究了应变率分别为1×10-3s-1、1×10-4s-1、1×10-5s-1条件下水饱和度对混凝土动力压缩效应的影响，得出如下结论：（1）随着应变率增加，混凝土应力应变曲线初始线性段斜率增加且非线性部分减小，形状发生了明显改变。随着应变率增加，混凝土动态抗压强度以及动力强度增长因子都增加，弹性模量增加，峰值应变减小。（2）随着水饱和度增加，混凝土静动态应力应变曲线产生明显变化。随着水饱和度增加，混凝土在静载以及动载下的抗压强度减小，动载时DIF 增大，即水饱和度越大，混凝土率效应越强。在应变率越高时，混凝土峰值应变随水饱和度增加而减小的趋势越明显，而弹性模量随水饱和度增加而增加的趋势越明显。（3）综合考虑应变率效应以及水饱和度影响提出了混凝土动力强度增长因子以及弹性模量的拟合公式，与试验结果相比其具备较好的吻合度。