泾河流域水沙联合分布特征分析及其不确定性评估

马川惠，黄 强，郭爱军

（西安理工大学 省部共建西北旱区生态水利国家重点实验室，陕西 西安 710048）

1 研究背景

径流与泥沙具有相关性，是非独立的二维随机变量。降雨冲刷地表造成水土流失，从而导致河流含沙量增加，造成河道淤积和洪水位的抬升，最终引发水患。以往对水沙概率分布特征的分析多以单变量法为主，侧重描述水或沙的单变量特征，忽略了二者间显著的关联性，对水沙过程的描述略显不足；若要对流域水沙特性有更加深入和全面的了解、实现水沙并举的科学管理方案［1］，综合考虑水沙变量相依特征，进而开展水沙二维随机变量的联合概率分析则尤为必要。

Copula 函数作为一种构造多维变量联合分布的有效方法，在水文学领域得到了广泛应用。Copula 函数的优点在于其不要求变量具有相同的边缘分布，任意边缘分布都可以通过Copula 函数连接构成联合分布，该联合分布里包含了变量所有的信息，在转换过程中不会产生信息失真［2］。丁志宏等［1］以潼关水文站汛期次洪过程中的洪峰流量和相应次洪过程中的最大含沙量系列为基础，运用Copula 函数方法构建了黄河中游汛期水沙联合分布模型并对其应用进行了探讨。周念清等采用Copula 函数建立洞庭湖流域水沙联合分布模型，分析洞庭湖流域水沙丰枯遭遇频率［3］。冯平等探讨了以Gumbel 分布为边际分布的二维联合分布模型，建立并探讨了联合重现期和条件重现期分布模型的实用功能［4］。陈子燊等［5］应用阿基米德极值Copula 与Kendall 分布函数构建不同历时暴雨组合的联合概率分布模式，分析各历时暴雨组合的遭遇概率、“或”重现期、“且”重现期和二次重现期，以出现最大可能概率的方法推算各组合的设计暴雨值。李天元等［6］基于Copula 函数构造洪水峰、量之间的二维联合分布，推导了两种具有统计意义的两变量联合设计值组合，即两变量同频率组合和条件期望组合。以清江流域隔河岩水库为应用实例，从防洪安全的角度考虑，推荐采用两变量同频率组合作为水库防洪设计值。

水文过程是一种受气候、气象、地形、地貌和下垫面等因素影响的复杂自然过程，蕴涵着确定性的动态规律和不确定性的统计规律。由于水文现象的极端复杂性以及人类认识水平的限制，使得对水文过程的认识存在着不确定性［7］。水文频率分析中主要采用参数模型方法，在此框架下包含着一般样本抽样、线型选取和参数估计等三个方面的内容［7-8］。其中，水文样本系列通常长度较短，样本对总体的代表性不高，基于观测样本开展的水文分析存在着显著的不确定性，进而影响管理决策的制定。如何在基于Copula 函数的联合分布模型中对这一不确定性加以合理考虑并对其进行定量评价，具有重要意义［9］。由此，采用Copula 函数研究水沙联合分布特征，同时量化样本不确定性对其影响则是本文主要研究目标。

泾河为黄河流域十大水系之一，是黄河洪水泥沙主要来源地之一。泾河流域暴雨集中，产流量集中，一次产流量大，含沙量也特别高，最大超过800 kg/m3。高强度暴雨形成高含沙水流，高含沙水流既有极强的输沙能力，又有很强的侵蚀能力［10］。要塑造协调的水沙关系，为水沙灾害的治理提供指导，就必须对流域的水沙分布特征有较为准确的分析和掌握。目前，国内外对水沙关系研究主要集中在，分析气候变化（主要为降水）、人类活动（水利工程、水土保持措施等）对流域减水、减沙效益的评估，以及流域产流产沙机制的影响方面［11］。在水沙联合分布模型及其应用方面，研究主要针对于流域水沙特征值或设计值以及水沙丰枯遭遇的变化情况［1，11-13］。而要为流域治理规划、生态恢复及防灾减灾等工作提供决策依据，还必须研究水沙序列固有的样本不确定性，因为水沙联合频率分析以及水沙设计值的不确定性，影响着流域水利水保工程修建规模的设计、流域水沙调控等方方面面，具有重要意义。

综上所述，本文以泾河流域控制站——张家山水文站为研究对象，提出基于蒙特卡洛法的两变量联合设计值不确定性量化方法。该方法基于Copula 函数建立水沙两变量联合分布模型，推求水沙两变量联合设计值组合——最大可能组合，利用蒙特卡洛抽样法分析样本不确定性对水沙联合设计值的影响，计算两变量设计值置信区间。本次研究可为水沙联合概率分析提供一种新的视角，并为其在水利工程中的应用提供典型案例。

2 研究区域概况与数据

泾河流域西起六盘山，东界子午岭，南沿渭北高原，北临宁夏、陕西交界的白于山麓。干流全长483 km，流域面积为45 421 km2［14］。流域多年平均降水量为516.7 mm，多年平均水面蒸发为800 ～1400 mm，年均径流量16.25 亿m3，年均含沙量132.2 kg/m3［11］。作为泾河把口站，张家山水文站控制泾河流域95 %的面积，属国家重要站，集水面积43 216 km2，距河口里程58 km。张家山水文站以上河段流经黄土高原，植被覆盖率低，张家山河段比降大，流速快，河流冲刷严重［15］。泾河流域地理位置见图1。

本文选取泾河流域张家山水文站1960—2012年实测月径流量与月输沙量资料，数据来源于黄河流域水文年鉴，已通过三性审查。图2为张家山站径流量与输沙量均值年内12 个月变化过程。由图可知，泾河流域汛期（6—10月）产水产沙量较其他月份显著增加。其中，汛期径流量占全年比71.09 %，输沙量占全年比96.73 %。故此，本次研究采用6—10月份径流量、输沙量之和，作为水沙联合分布模型输入数据。

3 研究方法

广义极值分布、对数正态分布、P-Ⅲ分布、Gamma 分布是水文分析中的常用概率分布类型［16-20］。用上述4 种分布拟合张家山水文站径流量与输沙量边缘分布，以AIC 准则选择最优的边缘分布；基于Copula 函数建立水沙联合分布模型，以AIC 准则选择最优的联合分布。基于此，计算径流量与输沙量的联合“或”重现期下的“最大可能组合”联合设计值，应用蒙特卡洛方法评估样本不确定性对水沙联合设计值的影响，利用二维自适应核密度估计方法计算该联合设计值的置信区间；为进一步分析该联合设计值的不确定性随重现期变化的关系，采用联合熵量化不同重现期下该联合设计值的不确定性。

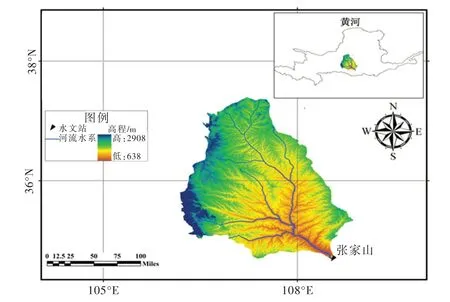
图1 泾河流域地理位置

图2 径流量与输沙量均值年内12 个月变化过程

3.1 水沙联合分布模型本文选取的4 种边缘分布概率密度函数如下：

P-Ⅲ分布概率密度函数：

Gev 分布概率密度函数：

Gamma 分布概率密度函数：

对数正态分布概率密度函数：

假设X、Y 分别表示年径流量与年输沙量，对应的设计值分别为x、y，其边缘分布分别为FX（x）、FY（y）。由Sklar 定理知，X 和Y 的联合分布函数可以用一个二维Copula 函数C 表示［21］

式中：F（x，y）为X 和Y 的联合分布函数；θ为Copula 函数的参数。

Copula 函数总体上可以分为3 类：椭圆型、二次型和Archimedean 型。其中Archimedean 型（分为对称Archimedean 型和非对称Archimedean 型）在水文领域应用最为广泛［3］。选用三种常用的Archimedean 型Copula 函数构造水沙联合分布模型，函数表达式如下：

Gumbel Copula 函数：

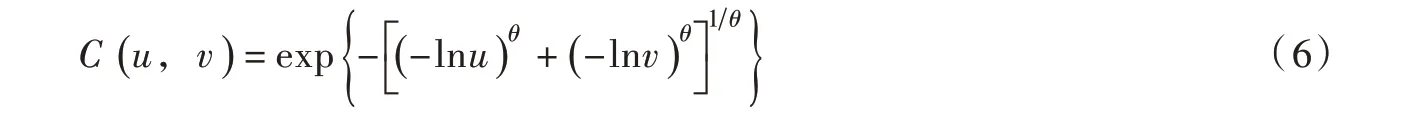
Clayton Copula 函数：

Frank Copula 函数：

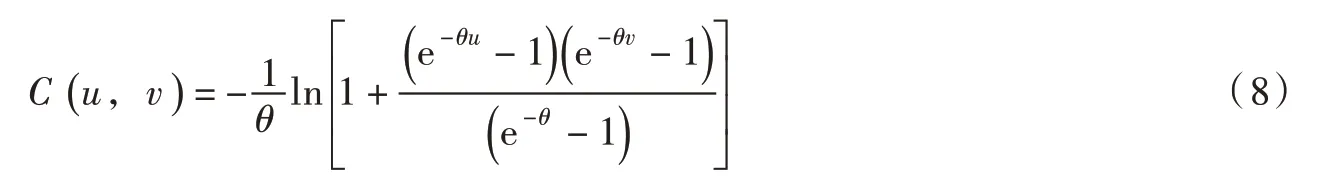
式中：u 和v 分别代表边缘分布函数，u=FX（x），v=FY（y）。

3.2 两变量联合重现期重现期是水利工程中一个设计标准的概念，是用来衡量水文事件量级的重要指标。陈子燊等［5］在研究排水排涝两级标准衔接的设计暴雨水平时，曾定义三种联合重现期，“或”重现期、“且”重现期与二次重现期。

为精简文章篇幅，本文主要分析“或”重现期下水沙联合设计值，其余类型重现期下水沙设计值分析方法与“或”重现期时相同。采用算符“ ˇ”定义两变量“OR”事件则事件的“OR”联合重现期（“或”重现期）为：

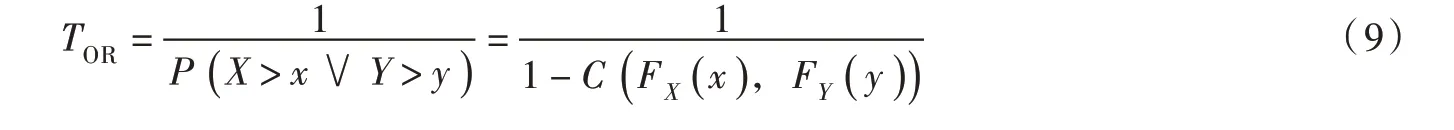
风险即非期望事件的发生概率，可用“OR”联合重现期表征径流量与输沙量组合遭遇的风险。“OR”重现期表示的是X、Y 这两个变量中任一变量的设计值被超越时的重现期。

3.3 两变量联合设计值对于单变量情况，若给定重现期T，相应的临界概率水平p，相应的分位数（设计值）其值是唯一的，且被广泛地应用于工程设计中。针对两变量情况，则变得相对复杂。对于给定的任一联合重现期TOR，在理论上存在无数种径流量输沙量组合（x，y）满足设计标准。这些（x，y）的组合可以用一条重现期等值线来描述。联合重现期等值线上的每个点，都代表一种水沙设计值组合，每种组合的联合重现期均等于同一个TOR值。然而在实际工程设计与应用中，决策者需要的是某一适当的水沙联合设计值或某一置信水平下水沙联合设计值的估计区间，针对这一矛盾，Salvadori 等人［22］提出一种具有统计意义的联合设计值组合——最大可能组合。最大可能组合是指（x，y）在某一重现期水平下，联合概率密度函数f（x，y）取最大值时的联合设计值组合模式。

求解方程如下：

3.4 基于蒙特卡洛的联合概率计算不确定性评估蒙特卡洛随机方法以概率统计理论为基础，可用来分析各种不确定性的问题［23］。本文应用蒙特卡洛方法，对样本进行多次重抽样，可评估样本不确定性对水沙联合设计值的影响。具体步骤如下：

（1）基于式（5）所示的Copula 函数，估计联合分布模型的参数；

（2）以上述基于Copula 函数的联合分布模型代表总体，从中抽取与观测值同等长度的二元样本，应用蒙特卡洛方法模拟2000 次；

（3）使用与基于观测值的水沙联合分布模型相同的估参方法估计基于模拟样本的联合分布模型的参数值，得到2000 组参数值与各参数95 %置信水平下的估计区间；

（4）在每一种参数组合下，由式（10）计算TOR=20、30、40、50、60、70、80、90、100年重现期水平下最大可能组合的水沙联合设计值。

3.5 联合设计值的二元置信区间选用最为常见的高斯函数作为核函数，文献［24］给出了多维核密度估计的定义：

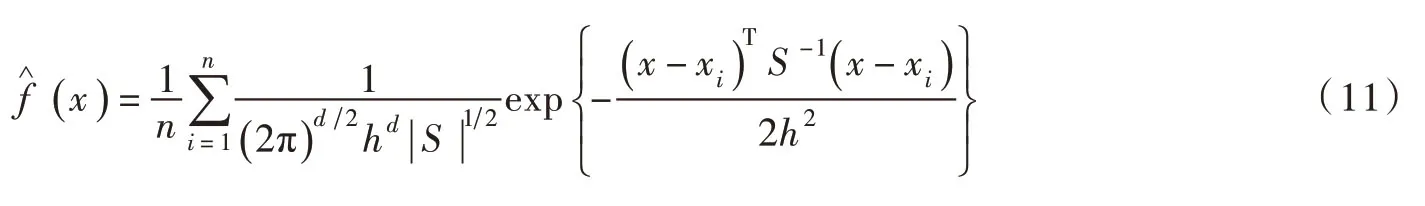
式中：x 为d 维向量；n 为样本容量；h 为窗宽；S 为样本协方差矩阵。

本文采用最小二乘交叉识别法（LSCV）计算窗宽h。当核函数为高斯函数时，可得下式［25］：

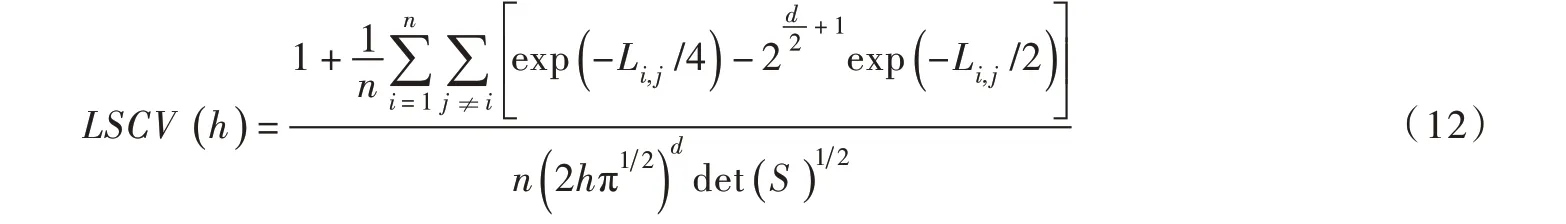
令式（11）中d=2，便可得二维自适应核密度估计模型。

应用二维自适应核密度估计模型得到联合概率密度函数后，用一个平面f（x，y）=C 来截取该函数的空间曲面，得到一组等概率密度轮廓线，在同一轮廓线内其密度相同。用R 语言emdbook 包中的HPDregionplot 函数可绘制某一显著性水平α下的等概率密度轮廓线，这一曲线包含了1-α的样本［26］。

3.6 基于联合信息熵的不确定性评估信息熵是信息的基本单位，是一种描述随机变量的分散程度的统计量。信息熵不仅针对于一维情况，对于更高维的情况，可以定义联合信息熵。例如，随机变量X 和Y 的联合信息熵可以用它们的联合分布 fX,Y(x，y)定义：

式中S 为 fX,Y(x，y )的定义域。

信息熵可以作为变量的分散程度，或称为不确定性的度量指标。信息熵越大，随机变量的分散程度越大，对该随机变量的值我们就越“不确定”［27］。

4 结果及其分析

4.1 联合分布模型为了研究泾河流域张家山水文站径流量与输沙量两个序列之间的相关性，本文采用Kendall 秩相关检验，检验联合分布模型输入数据，得到P=8.004×10-9。P 值小于0.05，故拒绝原假设，认为在0.05 的水平上两个序列具有显著的相关性。要进一步深入的了解泾河流域水沙耦合作用下的复杂水文事件，必须全面考虑径流、泥沙两个相关变量，建立水沙联合分布模型。

Copula 函数的参数估计方法包括矩法、核估计法、非参数估计法、极大似然估计法等。随机变量的边缘分布一般采用极大似然法估计和矩法估计，而Copula 连结函数的参数估计通常采用非参数估计法、适线法和极大似然法。以极大似然法估计4 种边缘分布的参数，结果如表1和图3所示。

K-S 检验（Kolmogorov-Smirnov Test）基于累积分布函数，用以检验两个经验分布是否不同或一个经验分布与另一个理想分布是否不同［28］。假设检验问题如下：样本总体分布服从某特定分布（H0），样本总体分布不服从某特定分布（H1）。设D 为F0（x）与Fn（x）差距的最大值，定义如下：

式中：Fn（x）为经验分布函数；F0（x）为假设的总体分布函数。

表1 边缘分布参数值

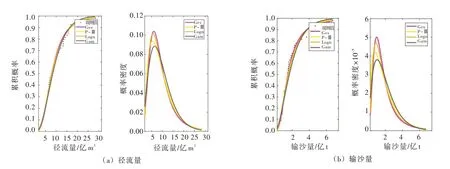
图3 边缘分布概率密度函数与累积分布函数曲线

当D＞Dα时，接受H1；当D≤Dα时，接受H0。

AIC 最小准则的原理是若欲从一组可供选择的模型中选择一个最佳模型，应选择AIC 值最小的模型［29］。AIC 值的表达式为：

采用K-S 检验法对边缘分布进行假设检验，并使用AIC 最小准则选择最优的边缘分布，结果见表2。经检验，张家山站数据服从假定4 种分布的P 值均大于0.05，无法拒绝原假设，因此认为通过了假设检验。径流量与输沙量的最优拟合分布均为对数正态分布。

基于Copula 函数建立水沙联合分布模型，以极大似然法估计Copula 函数的参数，结果见表3。由表3中AIC 值可知，应选取Gumbel Copula 为最优Copula 函数，其概率密度函数与累积分布函数三维图见图4。通过联合分布可以得到给定年径流量和年输沙量对应的联合概率，反之，给定年水沙联合概率和一个变量值，可以得到另一个变量的值。

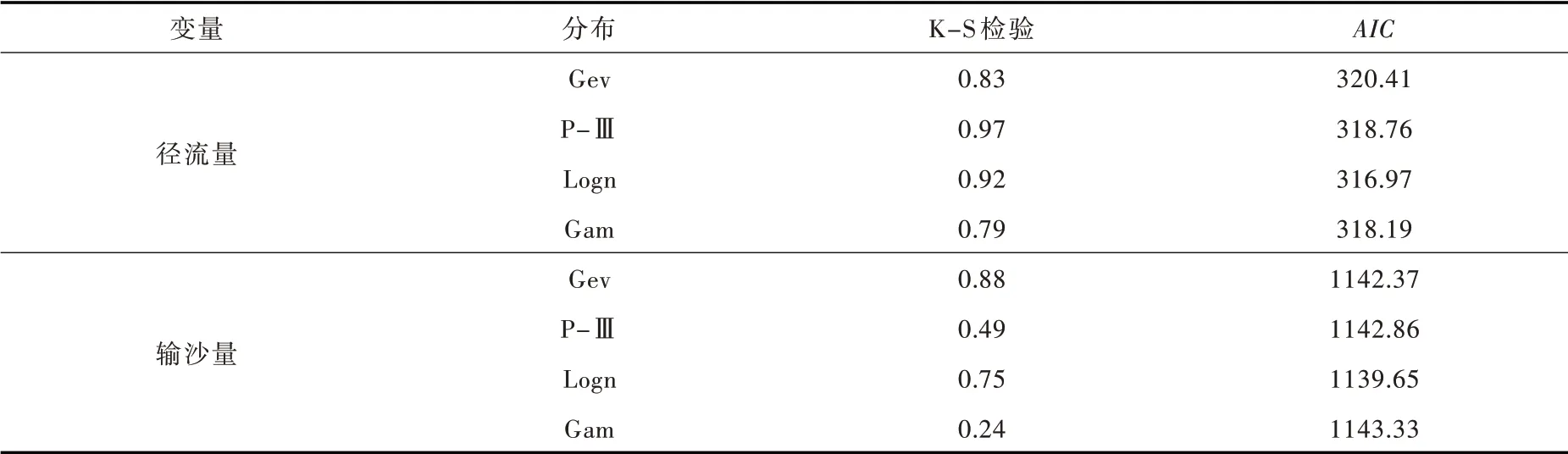
表2 K-S 检验与AIC 值

表3 联合分布参数与AIC 值

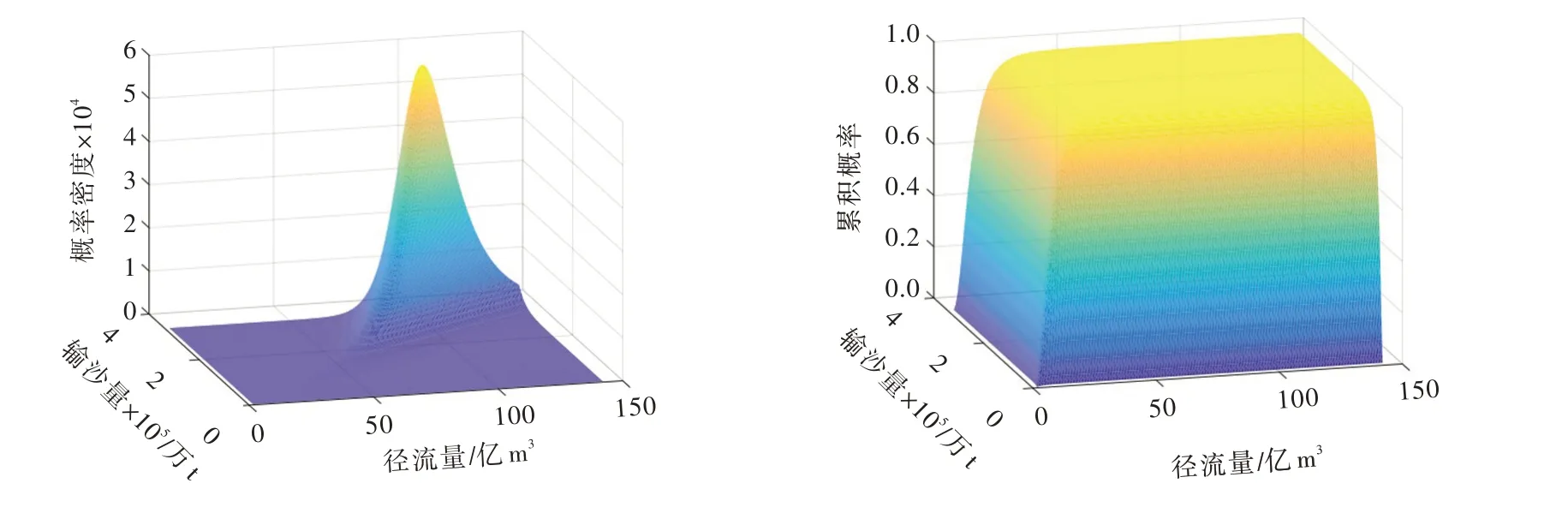
图4 概率密度函数与累积分布函数三维图

4.2 基于蒙特卡洛的联合分布模型不确定性评估在模型实际应用中，一个首先需要解决的问题就是参数的识别。不确定性理论的发展改变了传统的基于优化的参数识别体系［30］。为了获取更可靠的模型参数，不确定性思想认为通过一定的统计方法获得的多组参数具有更大的现实意义［31］。本文采用蒙特卡洛方法研究参数的不确定性，获得模型参数95%置信水平下的参考范围，为深入理解径流泥沙模型系统提供了有效途径。

联合分布模型参数的估计区间见表4。其中，参数变幅的计算参考相对误差，以参数置信区间宽度除以参数置信区间左边界值表征。由表4可知，张家山站联合分布模型呈现较大的不确定性。联合分布的参数θ变幅为55.65%，边缘分布的参数变幅因参数不同而呈现明显的高低变化，u 未超过16.10%，但σ大约在50%。

表4 联合分布模型参数95%置信区间

绘制“或”重现期等值线图，如图5所示。从中可知，所构建的水沙联合分布模型可以给出不同程度径流量和输沙量遭遇组合的重现期。史黎翔［32］在研究多变量水文事件重现期时指出，“或”重现期的危险区域偏大，但其对危险事件的定义明确，可满足一些特定的应用需要。在工程应用中，一般选用某一“或”重现期作为安全或风险设计控制值。通过泥沙频率与洪水频率的组合，可以确定河道可能的时段最大、最小淤积量，抬升速度以及堤防的加高规划指标等［33］。同一重现期对应不同的水沙组合事件，选取适宜的典型洪水过程线和含沙量过程线，采用同概率放大法，即可给出相应的若干组具有相同重现期的不同设计洪水过程线和设计含沙量过程线相搭配的水沙配比体系，从而为规划调度中水沙条件的选取与概化提供基础的方向性指导［13］。综上所述，水沙组合遭遇频率是流域的重要参数，为开展流域治理规划、生态恢复及防灾减灾等工作提供决策依据。

水沙联合重现期与联合设计值的准确与否关系到流域水利工程建设是否经济合理，运行是否安全可靠。采用设计标准过高，会造成工程规模过大，必然增加工程投资；反之，如果设计标准过低，会造成建设工程规模过小，不利于水利水电工程发挥其实际功能，导致工程重大失误，更有甚者导致工程失事，造成巨大的生命财产的损失［32］。经相关性检验，泾河流域水沙存在显著的相依性，不考虑相依性的水沙频率分析及设计值推求存在误差与风险。综上所述，研究泾河流域水沙联合重现期与联合设计值的相关内容，其成果不仅有助于了解泾河水沙特性，还可对泾惠渠渠首引水限沙及工程改建提供一定的技术参考，是一种新的设计参考思路。

水文频率分析过程中，采用的水文样本系列一般较短，通常只有40、50年的资料系列，样本对总体的代表性存在偏差，使得基于给定样本系列推断出的总体参数存有较大不确定性，进而影响水文设计值的可靠性。如何定量评价这种不确定性，并在工程设计中加以合理考虑，在工程水文设计中得到了广泛重视［34］。

在TOR=20年下，推求最大可能组合联合设计值为（22.73 亿m3， 54924.96 万t）。而本文采用蒙特卡洛方法，对原始样本系列进行重抽样，获得给定条件下水文设计值的区间估计。如图5所示，在水沙联合分布重现期等值线图中，TOR=20年下联合设计值50 %、75 %、95 %置信水平下的二元估计区间以一个二维平面的形式呈现。联合设计值95 %置信水平下的二元区间在图中覆盖的面积较大，约跨越了5年至50年的重现期。

信息熵可以作为评价随机变量不确定性大小的指标，信息熵越大，不确定性越大。计算TOR=20 至TOR=100年重现期水平下（计算间隔为10年）水沙联合设计值的联合熵，如表5所示，定量评估联合设计值的不确定性。由表5、图5可知，TOR=20年下，联合设计值已存在较大的不确定性，且随着重现期水平的增加，联合熵呈现明显增加的趋势，说明联合设计值的不确定性在增大。

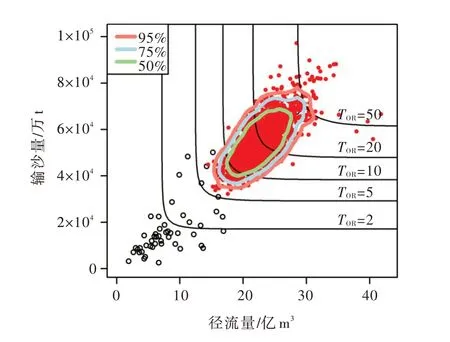
图5 联合重现期等值线与联合设计值二元置信区间图

表5 不同重现期水平下联合设计值联合熵统计

泾河流域土地平坦，农业发达，矿藏丰富，经济开发潜力很大。耕地占全流域面积近1/3，是西北地区著名的产粮区。泾河流域水沙联合分布模型及水沙联合设计值如此之高的不确定性对流域水库设计、防洪减沙等方面提出了巨大挑战，在制定防灾政策时应引起决策者的重视。

5 结论

泾河流域水土流失严重，生态脆弱，本文以高含沙河流泾河流域为研究对象，建立径流量与输沙量联合分布模型，进行水沙组合遭遇风险分析；对水沙联合分布模型进行基于蒙特卡洛的不确定性评估，计算TOR=20 至TOR=100年（计算间隔为10年）重现期水平下的“最大可能组合”联合设计值及其联合熵，绘制TOR=20年下联合设计值的二元置信区间图。结论如下：

（1）绘制了“或”重现期下等值线图，为泾河流域防洪调度工作和防洪减灾标准等提供了综合考虑水沙耦合情况下新的描述基准，将其描述范畴由X年一遇的洪水过程拓展到X年一遇的水沙过程。

（2）TOR=20年下，联合设计值95 %二元置信区间在联合重现期等值线图中约跨越5年至50年的重现期，表现出较大的不确定性，对流域工程设计值的确定提出了巨大挑战，且随着重现期水平的增加，联合设计值的不确定性随之增加。

（3）泾河流域水沙联合分布模型及水沙联合设计值如此之高的不确定性对流域水库设计、防洪减沙等方面的影响如何处理，有待进一步研究。