基于电大学员情况对微分教学的改进
陕西省安康职业技术学院 荆荣丽
伴随着社会文明的进步,广大劳动者对知识的要求愈来愈多、愈来愈全面,深度愈来愈强。当然,知识越深,难度就越大。比如对于理工生来说,高等数学就是一门基础课,而微积分则是高等数学教学的重点、难点。电大招入学员大多数知识层次低,数学基础知识较差,学习积极性弱,自觉性不强,自我约束能力不足,学习态度不端正,而且缺乏踏实努力、刻苦钻研的学习精神,在数学学习意识、学习方法、学习能力上比较欠缺,这就要求从事一线教学的老师们改变思想,转化理念,在教学设计上多动脑筋,多想办法,如利用比较法、找规律等手段,通过引导、启发、鼓励等方式调动学生的求知欲,从而激发学生的学习积极性。结合以上情况以及笔者自身的教学心得,提出一些教材编排上的设想和教学方法上的改进。
一、微分概念的分析
在高等数学教材中,微分概念一直被称之为“函数增量的线性主部” 。本人从事多年的微积分教学任务, 从严密性很强的数学理论体系来说,把微分理解为“增量的线性主部”是非常合理的选择,但考虑到电大学生的理解思维能力,接受到这样晦涩难懂、专业性强的定义,无疑增加了学生对微分概念的学习难度。但若避开数学严密抽象思维的特点,转用形象直观思维,形象化地给出微分定义,就可形成微分教学的新方案。无论是专升本教材还是现阶段的高起专教材,关于微分这一节的教学不外乎引例、导入概念(用增量的线性主部来定义微分) ,推出可导、可微的等价关系,再在数形结合的途径中讲述其几何意义,然后给出微分的运算法则、基本公式等,让学生能熟练计算微分,最后回归客观实际,讲明微分的应用。可以看出,这种教学模式中,微分的教学内容抽象,微分的教学环节又多,这既加重了学生的学业负担,又有悖于低基础学员教学的时效性原则。为改变以上状况,改革高职高专院校以及电大高数微分的教学方案,是我们必须探讨的一个问题。
一些学者强调从积分和微分的联系的角度讲授微积分。一般来说,微分是研究事物运动的瞬间改变量,积分是研究事物运动的区间改变量,如人的头发是无时无刻不在生长着,微分就是研究头发的瞬间生长量,积分则是研究头发在某一区间,例如一个月的生长量。微分和积分从运算角度考虑,可以这样说,减法产生微分,加法产生积分,微分和积分是对立的统一。它统一于积分运算。
目前学生擅长用微积分解题,但是概念理解不深,如果只强调计算而忽视概念的教学,将会妨碍微积分进一步深入教学,但教学时间有限,学生的概念理解与技能发展似乎成为一对矛盾。该如何有效地进行微积分概念教学? 在接下来的小节里,将主要讨论微积分概念教学的措施。
二、微分的概念
微分(differential)最初带有 “差”的意思,所以,微分表示函数增量的近似值。如果误差是Δx的高阶无穷小,则称函数在该点是可微的。通过下面引例,详细指出微分的差的含义、线性近似、误差等,代替原来那种一带而过、蜻蜓点水、语言不详的表达方式。
例1 要给一个半径为r0的球表面涂上油漆,油漆的厚度为Δr。试计算这层油漆的体积。
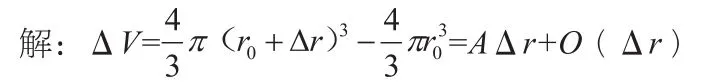
用一次函数的增量近似代替三次函数的增量,足见微分在简化运算中的作用。数学内涵是一样的,实际背景则更丰富,在学生得出相关结论后再将其推广为一般的误差估计,这样易于学生接受。
例2 考察自由落体运动S(t)=gt2,位移的增量。
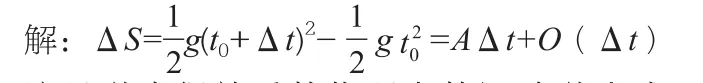
这是学生很熟悉的物理上的运动学公式,可以和位移公式S=v0t+gt2联系起来,这样学生自然就可以将公式中的A与速度v0即S'(t0)联系起来,Δt2与O(Δt)联系起来,从而得到ΔS≈dS=S'(t)Δt。
通过微分三角形,借助凹凸两种函数,详细解释微分的几何意义为函数在x点的切线的增量,微分概念蕴含着以直代曲、线性近似的思想。
三、微分计算
在微分计算这一教学环节中,首先讲解微分与导数的关系、微分的几何意义。在高中阶段,同学们已经学过导数,熟悉导数的基本公式和导数的运算法则。在讲微分时,联系导数与微分的关系,既体现了知识内容衔接相辅相成,同时也增加了学生对知识的熟悉度,不会产生对新知识的恐惧和畏难情绪,有利于学员更好地了解微分,方便计算以及后期对微分的应用。
1.利用导数计算微分
导数也叫微商,即函数的微分除以自变量的微分,所以,函数的微分自然就等于导数乘以自变量的微分。因此,微分公式如下:

微分的运算法则也可以由导数的运算法则得出,在这里就不再赘述。
2.一阶常微分方程
一阶常微分方程正常教学用时是4课时,在不降低大纲要求的前提下,及时调动学生自主学习,鼓励学生加强对比,提高其观察能力和实际学习效果,可以对教材进行一定的改变。
首先介绍一阶常微分方程的概念,然后列出以下常见类型及其特征:
(1)y'=f(x)型。其特征是:①左边是一阶导数y';②右边是自变量的函数。这类方程是一阶常微分方程的最简单形式,方便易解,是解微分方程的基础,为后面讲解高阶微分方程降阶做好铺垫。
(2)y'=f(x)·g(x)型。如果方程能把y的一阶导数转化成x的函数与y的函数乘积的形式,也就是说把x和y分离开,我们把它叫“可分离变量的微分方程”。其特征是:①左边是一阶导数y';②右边是自变量的函数与y的函数的乘积。
(3)型。如果方程能把y的一阶导数表示成的函数,我们就把它叫“齐次微分方程”。其特征是:①左边是一阶导数y';②右边是自变量与y的商 的函数。
(4)y'=f(x)·y+g(x)型。如果方程能化成这种形式,我们就把它叫“一阶线性微分方程”。其特征是:①左边是一阶导数y';②右边是线性关系,y'和y都是一次的;③f(x),g(x)都是x的函数。
给出这几种常见形式,并列举出每种形式的特点,方便学员观察、比较、理解。同时,一边讲形式一边举例说明,这样给予启发、引导,让学员有更充足的时间观察、思考,掌握知识快捷,使得他们有更高的兴趣深入探索研究。
接着,给出笼统的例题,从混合形式中分辨出每个题目的形式,然后归类。让学员从混合状态下根据这四种形式的特点分辨出所属形式,方便后面“求解微分方程”的理解和掌握。
最后,通过与例题相似的练习提高学员对每种微分方程的分辨能力,然后再进行解法的讲解。这样安排教学,符合接受知识的自然规律,适合数学基础较差的学员模仿、套形式的学习方式。
四、改进教学的效果
笔者从事数学教育以来,既带有高职数学,也带有电大高等数学的面授课。通过教学实践表明,在相同的授课时间内,改变微分部分的教学方法后,更利于培养学生的数学思想方法以及应用数学思想方法的能力,让学生对微分思想有了更深刻的认识,更利于他们理解和掌握专业知识。今后要结合专业特点,适应高职课程改革的新形势,以满足专业需要为原则,以培养应用能力为主线,提高高等数学的教学质量。
总之,教学以传道授业为宗旨,目的是让学生学艺受用。甚至有学者认为,微分教学要改变教学顺序,先讲微分再讲导数,把颠倒的历史重新翻倒过来,这也符合客观事物运动变化的规律。先研究事物运动的瞬间改变量,再研究事物运动瞬间变化率,这是顺理成章、易学易懂的快事。但这样的变更太广,我们目前也只能拭目以待。

