基于工况风险评估的叉车门架多工况拓扑优化
邹 坤 侯 亮 卜祥建 方奕凯
厦门大学航空航天学院,厦门,361005
0 引言
门架系统作为叉车提升货物的主要承重结构,其强度及刚度对叉车的安全性起着决定性作用[1],分析门架系统的准确力学特性是门架结构设计及优化的基础。但门架系统各部分之间存在大量的接触,高度的接触非线性使门架在整体有限元分析时难以收敛,无法实施进一步的结构优化,因此在进行叉车门架结构的拓扑优化前需解决其非线性仿真分析问题。此外,叉车门架作业工况繁多,进行优化设计需考虑各工况的综合影响。现有的多工况拓扑优化方法在分配工况权重系数时,主要依靠经验等主观因素,缺乏客观、准确的工况权重系数分配方法。
在门架系统的有限元分析方面,文献[2-3]采用局部分析的方法,分别计算门架各部件的载荷及边界条件,各部件单独进行有限元分析。而叉车作业工况繁杂,局部分析法不仅效率低下,也无法满足拓扑优化的要求。在多工况拓扑优化领域,文献[4-5]采用线性加权方法将多工况下最优问题转化为单目标问题,但对于非凸优化问题(即有两个目标冲突时),线性加权法不能确保得到所有的Pareto最优解。折中规划法能够很好地解决上述问题。文献[6-10]采用带权重的折中规划法,解决了优化中柔度最小与一阶固有频率最大之间的冲突。但无论采用线性加权法还是折中规划法进行多目标转化,都会遇到如何分配工况权重的问题。多数研究人员在分配工况权重时依靠经验或采取平均原则:文献[11]根据经验分配多工况下刚度目标与频率目标的权重;文献[4-6,8-10]在分配不同工况权重时视各工况同等重要,即不同工况取相同的权重系数;文献[7]采用决策论中层次分析法来计算不同工况的权重系数。但不论经验法、平均分配法还是层次分析法,都存在较多的主观因素。文献[12]虽然使用正交试验法来获取客车车身结构多工况拓扑优化的最优权重,但需要进行反复试验,在实际操作时比较繁琐。
本文研究了接触非线性有限元分析理论,构建了基于固体各向同性材料惩罚(solid isotropic material with penalization,SIMP) 法的单工况拓扑优化数学模型及基于带权重的折中规划法的多工况拓扑优化数学模型;在3种典型工况下进行了叉车门架系统的整体非线性静力学分析,并通过算例验证非线性分析的准确性;根据优化结果对门架结构进行改进设计,并对改进结果进行分析和讨论。
1 非线性有限元分析理论及拓扑优化数学模型
1.1 非线性有限元分析理论
接触问题在力学上属于高度非线性问题,包括由大变形引起材料非线性和几何非线性,以及接触界面边界非线性。接触界面非线性源于2个方面[13]:其一,接触区域的大小和位置事先未知,且随着时间变化,需要在求解过程中确定;其二,接触条件的非线性,接触条件包括①接触物体的不可相互侵入,②接触力的法向分量只能是压力,③接触面切向的摩擦条件。上述条件区别于一般的约束条件,属于单边性不等式约束,具有强烈的非线性。
借助有限元软件,可以准确地模拟接触条件,解决模型中接触非线性难收敛的问题。接触面之间的接触属性包括法向作用和切向作用[14]。①法向作用:默认为“硬接触”(即接触面之间的接触力大小不受限制),当接触压力变为负值或零时,解除接触面相应节点上的接触条件,两接触面分离。②切向作用:常用库仑摩擦模型,库仑摩擦计算公式为τcrit=μp(其中,τcrit为临界切应力,p为接触的法向压力,μ为摩擦因数)。此外,接触设置还有滑移公式的选择及接触面过盈量的设置。
对于非线性问题,有限元软件多采用Newton-Raphson算法来求解。即把分析过程划分为一系列的载荷增量步,每个增量步依次进行迭代求解,所有增量响应的线性叠加即为非线性分析的近似解。
1.2 拓扑优化数学模型
SIMP法是在相对密度法的基础上提出的,即带有惩罚因子的相对密度法。SIMP法引入一种假想的相对密度在0~1之间可变的材料,假设设计材料的宏观弹性模量与材料密度成某种非线性关系,采用惩罚因子约束抑制相对密度介于0和1之间的单元[15],使材料相对密度向0或1聚集。
在拓扑优化领域,最常用的方法是刚度拓扑优化。工程中通常把刚度最大问题等效为柔度最小化问题来研究,柔度值为单元总应变能值,计算与提取较方便[8]。基于SIMP变密度法,以结构的柔度最小为目标函数,以体积为约束条件的单工况拓扑优化数学模型如下:
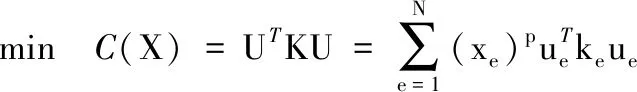
KU=F
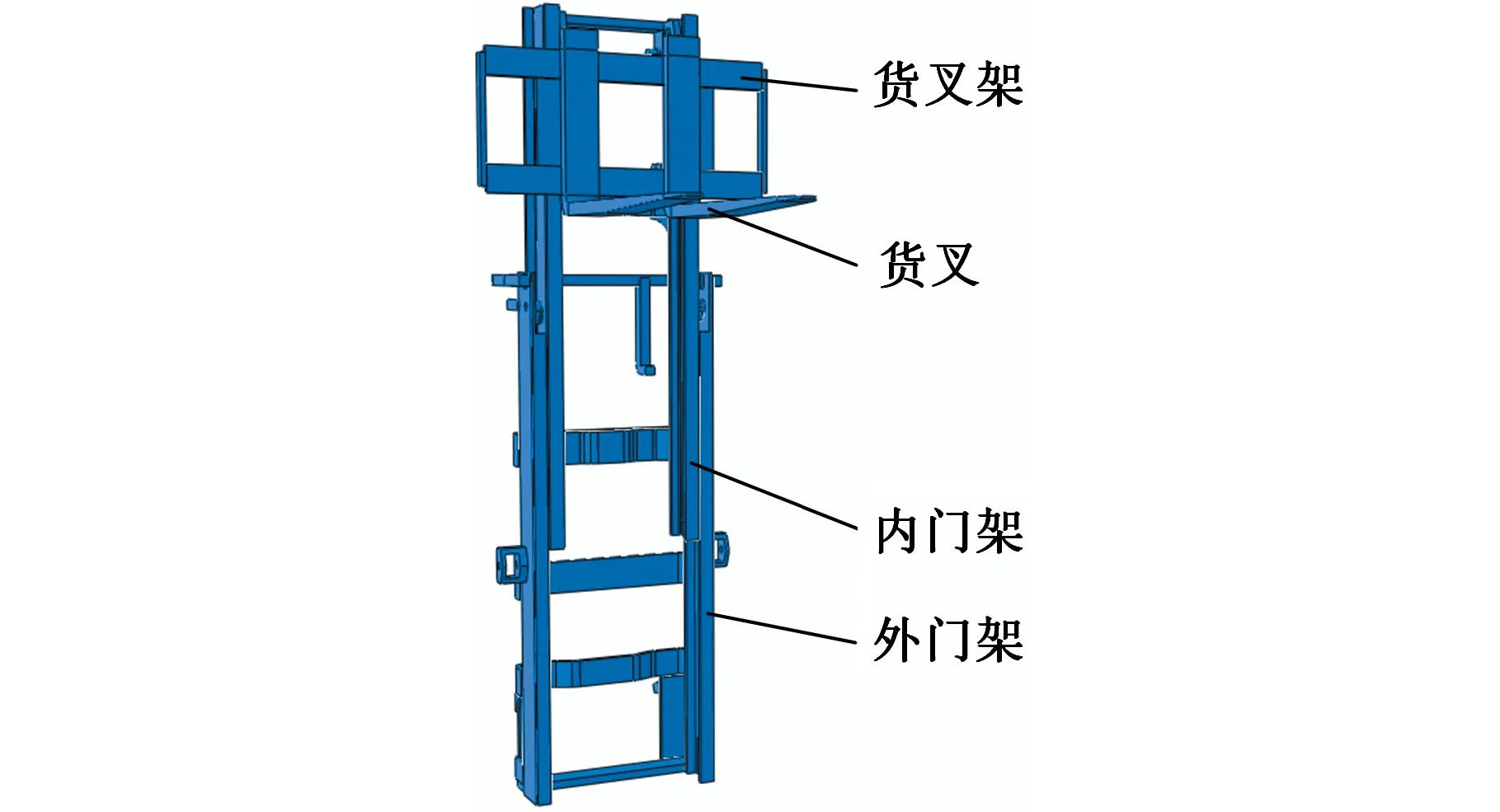
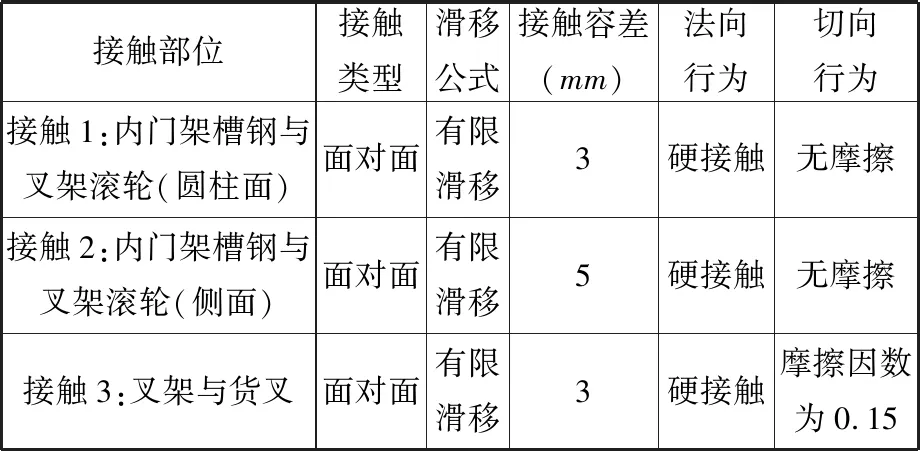
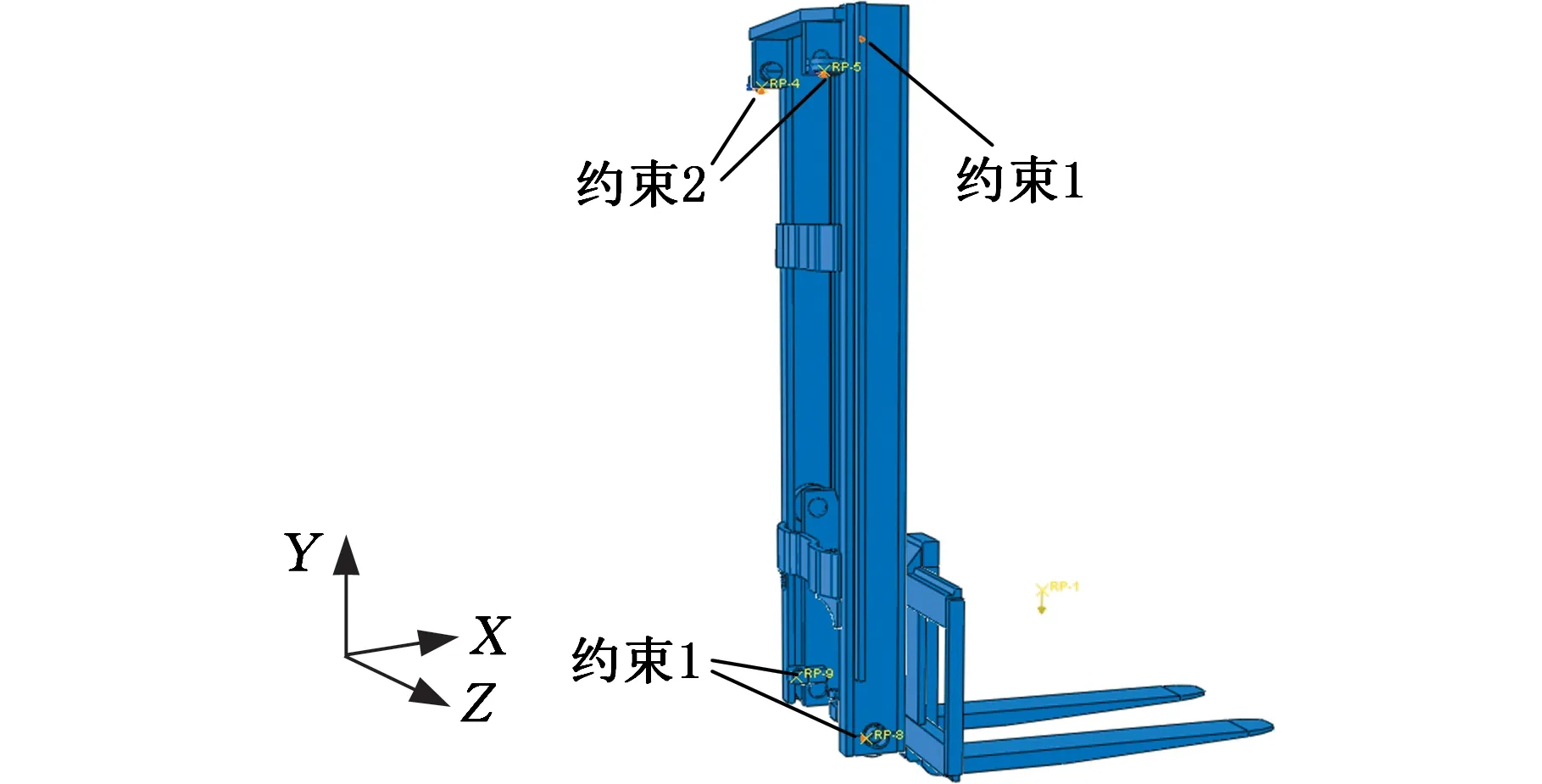
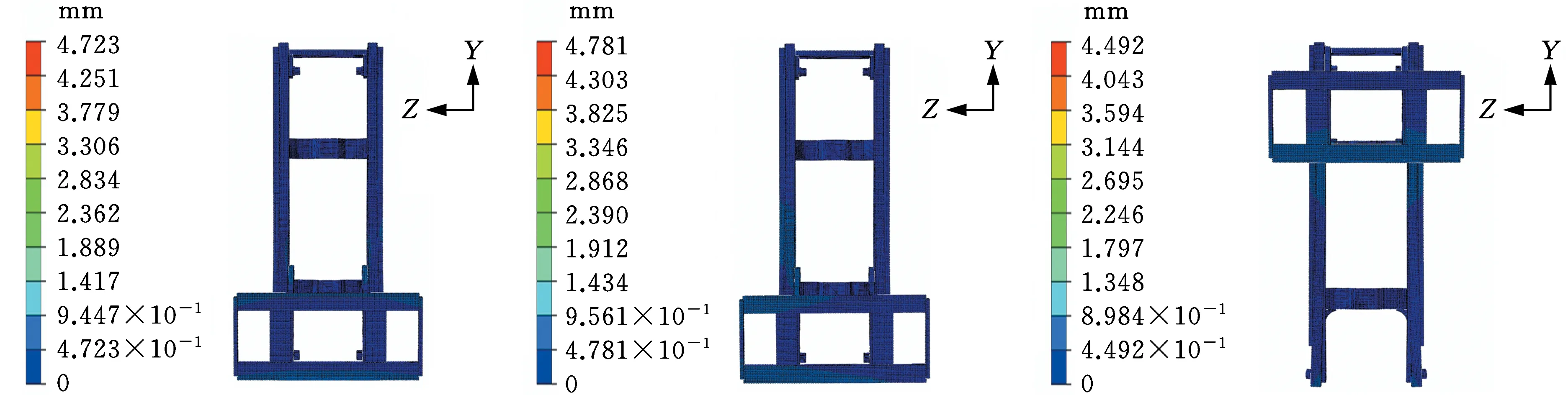
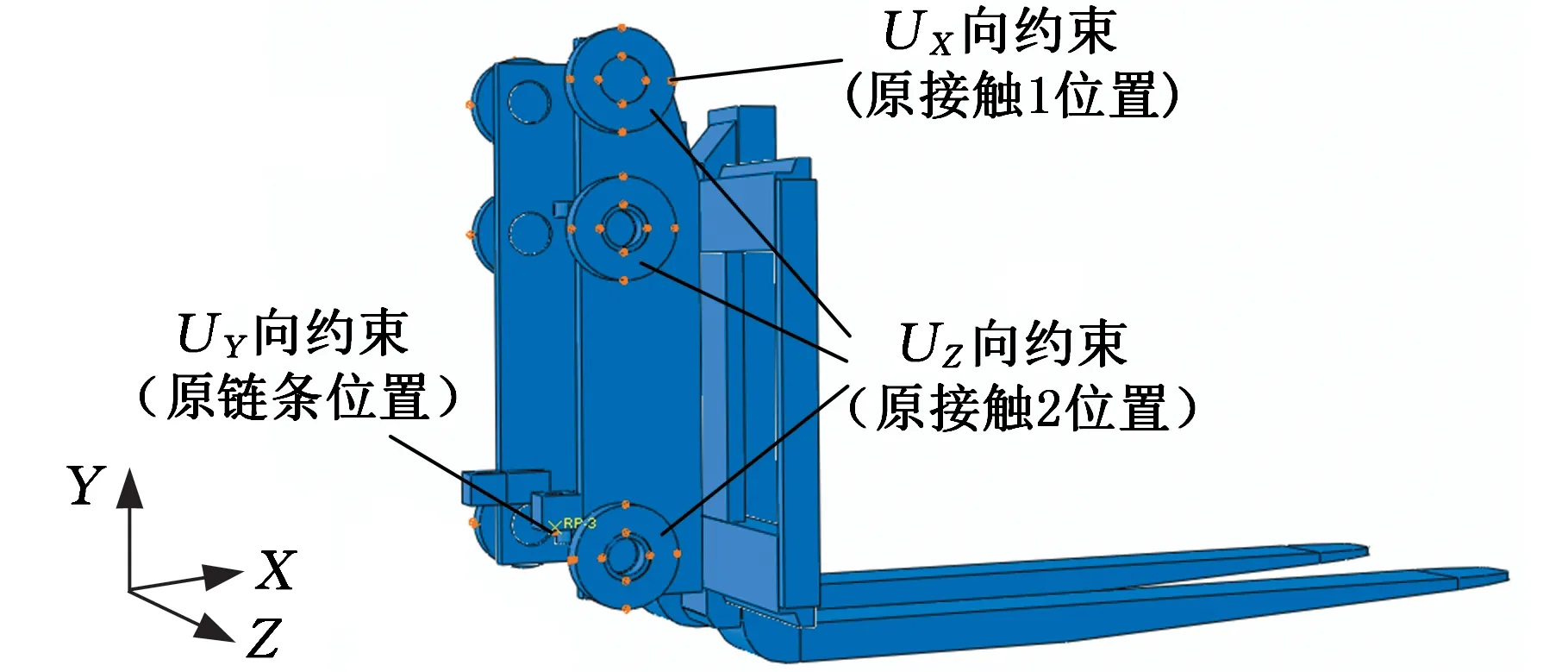
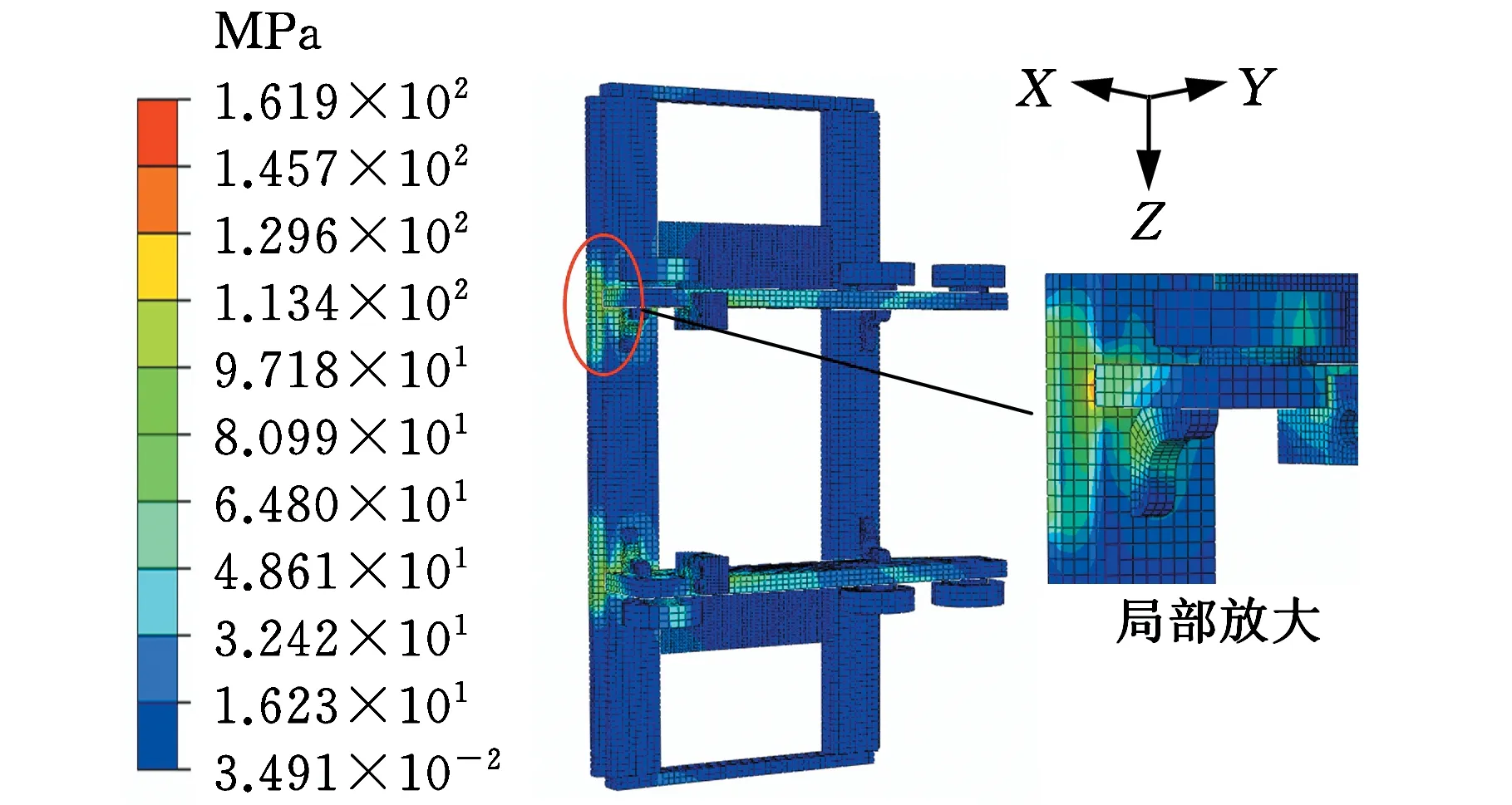
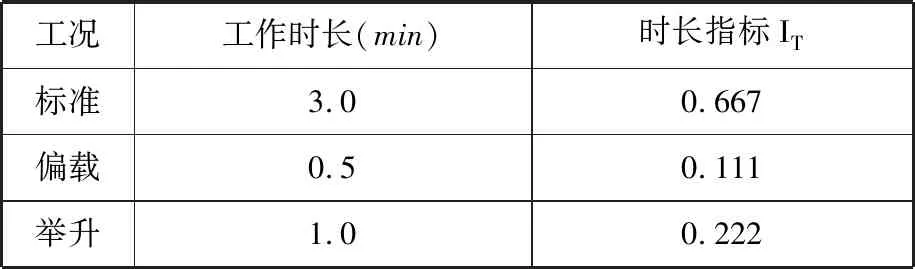
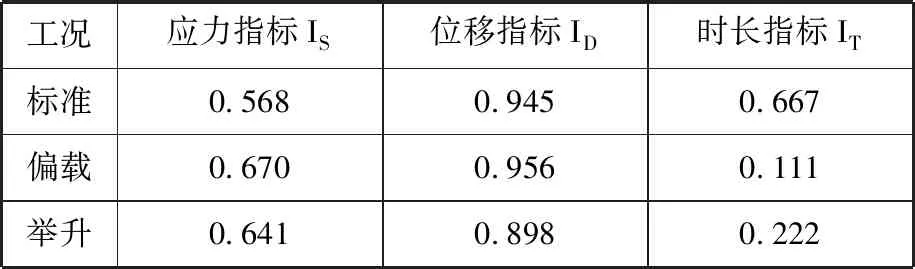
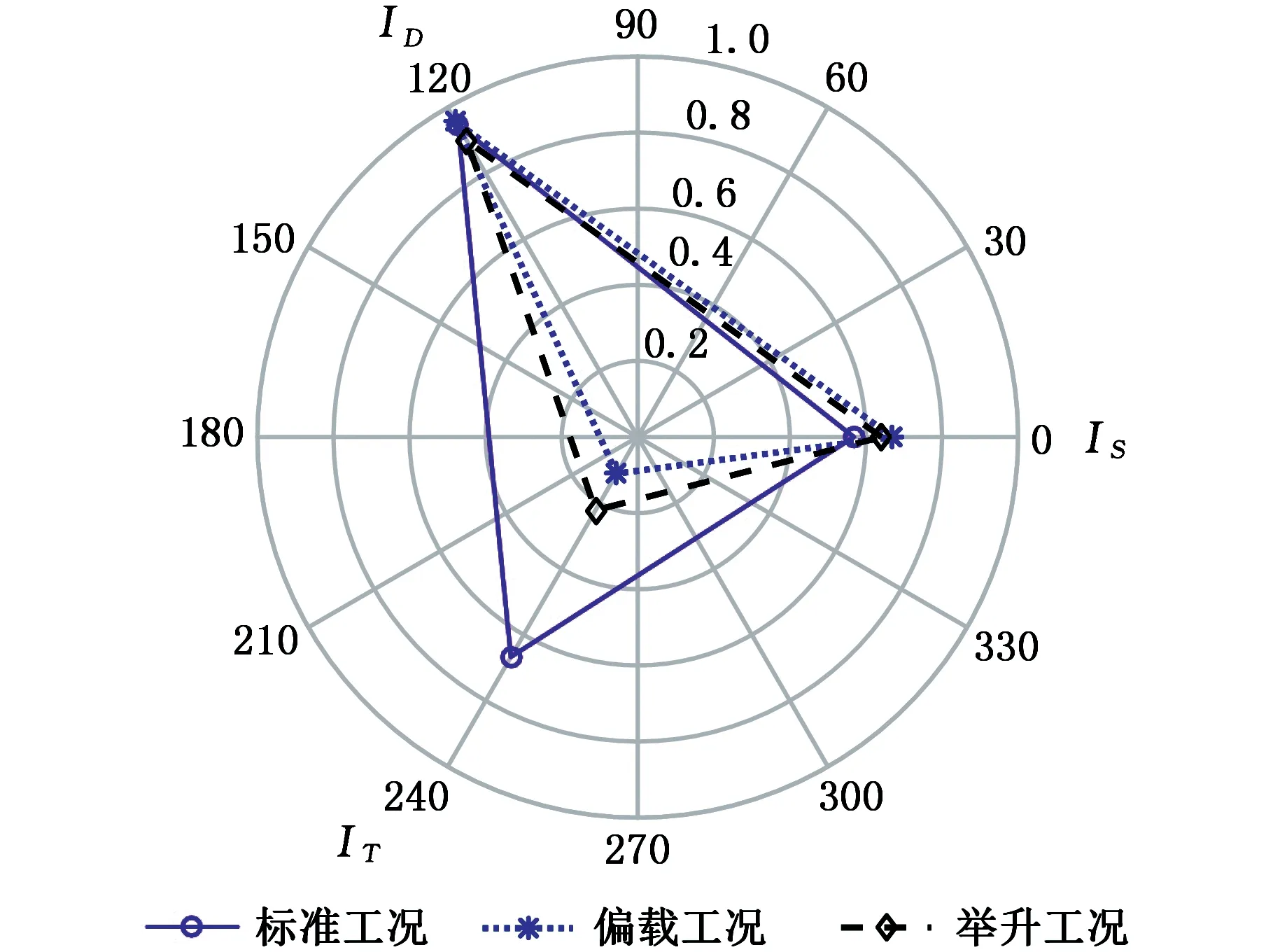
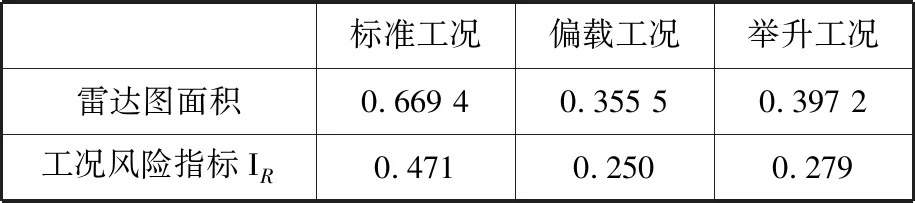
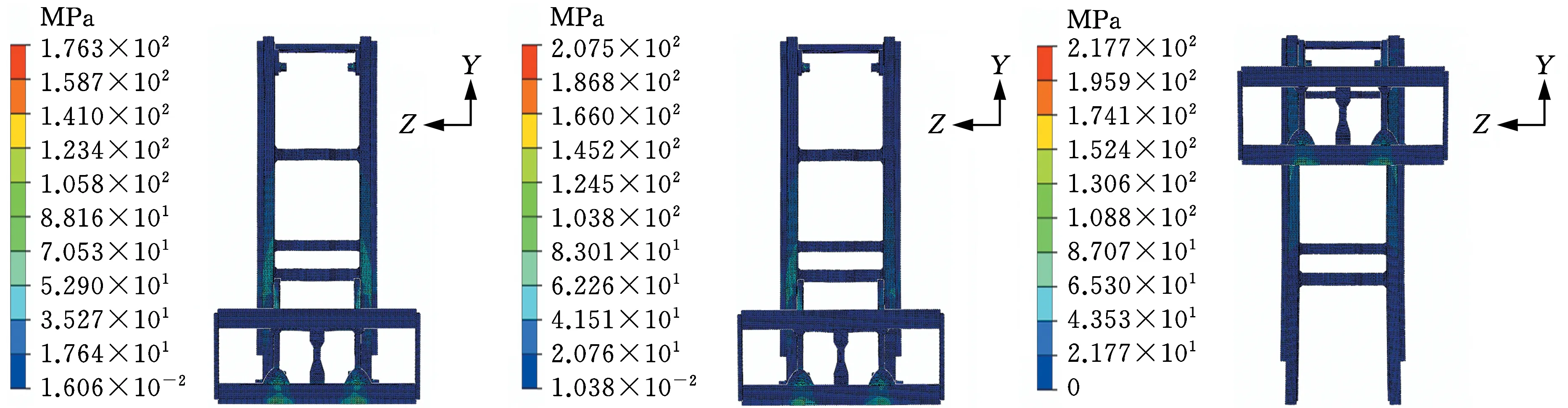
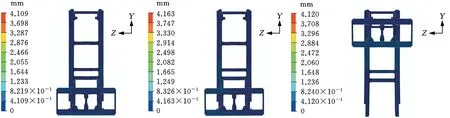
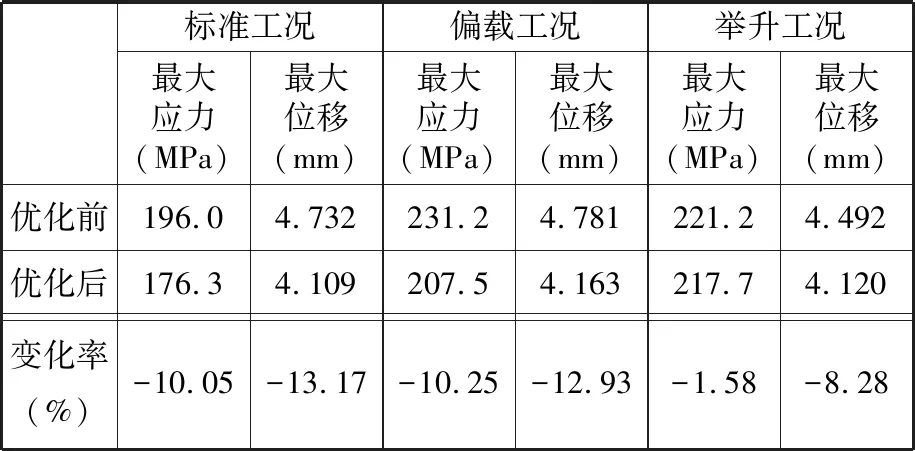
0 式中,X为设计向量(即所有单元的相对密度向量);C(X)为结构的柔度;F为载荷矩阵;U为位移矩阵;K为整体刚度矩阵;xe(e=1,2,…,N,N为单元总数)为单元相对密度;ue、ke分别为单元位移矩阵和单元刚度矩阵;V(X)为在设计变量状态下的结构有效体积;V0为结构原始体积;f为材料用量的百分比(体积系数);xmax、xmin分别为单元相对密度的上下限,取xmax=1,xmin= 0.01;p为惩罚因子,该模型一般取p=3。 在多工况下的刚度拓扑优化问题中,每一个载荷工况将对应不同的最优拓扑结构[16],因此,多工况拓扑优化属于多目标拓扑优化问题,可利用折中规划法将其转化为单目标问题。由折中规划法可得多工况拓扑优化的数学模型: (1) 以某平衡重式内燃叉车3 m标准门架为例进行静力学仿真分析。根据叉车作业过程中货物位置状态的不同,将叉车作业过程划分为3种典型的工况:运输状态下的标准工况,货物重心偏移的偏载工况,举升货物时的举升工况。由于门架系统的模型较大,故为了提高计算效率、节约计算成本,只选取门架系统的内门架、货叉架及货叉部分作为研究对象,在有限元软件ABAQUS中,通过合理设置接触条件,实现了3种典型工况下内门架-货叉架-货叉系统的整体非线性静力学分析。 叉车门架接触非线性有限元分析流程见图1。 图1 有限元分析流程Fig.1 Finite element analysis process (1)几何清理。去除小尺寸圆角、倒角、孔及凸缘等;删除链条、液压缸等连接及动力传递型零部件,并用耦合、约束、载荷等方式进行等效替代;将轴承简化为套筒,轴承轴简化为阶梯轴。简化后的门架模型如图2所示。 图2 简化后叉车门架模型Fig.2 Simplified model of door frame of forklift (2)网格的划分。门架零件板材的厚度为18 mm及以上,因接触部位的直接接触面与对应背面的应力差值较大,为保证分析的准确性,采用体网格对门架进行网格划分。为保证网格质量,整体采用线性六面体单元C3D8R进行网格划分;局部网格不协调处采用线性四面体单元C3D4进行划分;板厚方向依据材料厚度不同,划分单元层数为2~4。模型共有六面体单元104 910个,四面体单元7 030个,节点153 887个。门架材料为16Mn,密度为7 870 kg/m3,弹性模量为212 GPa,泊松比为0.310,屈服强度为345 MPa。 (3)接触的定义。所有接触均采用面对面接触[17],因为接触体刚度相近,主从面的选择对结果无影响;滑移公式为“有限滑移”,法向作用为“硬接触”,且接触后可分离;切向作用采用Penalty摩擦公式,设置无摩擦与摩擦因数为0.15两种情况。具体接触设置情况见表1。 表1 接触设置 (4)载荷及边界条件的设置,提交计算。该型号叉车的额定载荷为3T,安全系数取1.5,计算时载荷取额定载荷的1.5倍(即45 kN)。3种典型载荷工况的门架有限元模型及载荷见图3。3种载荷工况的约束条件均相同,见图4。详细工况参数及载荷、约束施加情况见表2。其中,标准工况为低位运输状态;偏载工况取极端工作状态,即货物重心偏移到一侧货叉上;举升工况取最危险状态,即货物在最高点。 (a)标准工况 (b)偏载工况 (c)举升工况图3 各载荷工况有限元模型及载荷Fig.3 Finite element models and loads of differentloads conditions 图4 各载荷工况约束Fig.4 Constraints of different load conditions 工况载荷高度(mm)偏载量(mm)载荷中心距(mm)载荷FY(kN)约束标准3000600-45偏载300175600-45举升1 6000600-45约束1:内门架挡板与下滚轮轴X移动方向自由度约束2:液压杆上支座X、Y、Z移动及旋转方向自由度 原始门架结构在不同工况下的应力云图和位移云图分别见图5和图6。由于在实际工作过程中货叉不易损坏,故本文只研究内门架和货叉架的强度及刚度状况,其静力学分析结果如下: (1)在标准、偏载、举升3种工况下,内门架和货叉架的最大应力依次为196.0 MPa、231.2 MPa、221.2 MPa,最大位移依次为4.732 mm、4.781 mm、4.492 mm。门架强度满足各载荷工况的强度要求,在偏载工况下门架的强度及刚度最差,所以叉车作业中应尽量避免偏载的发生。 (2)内门架上下横梁和货叉架左右中板在三种工况下综合的最大应力为231.2 MPa,且绝大部分区域的应力小于100 MPa,远小于门架材料的屈服强度345 MPa,门架结构存在强度冗余,有轻量化设计的空间。 为了验证整体非线性有限元分析的准确性,以标准工况下的叉车货叉架为例,进行非线性分析及线性分析对比。非线性分析(整体分析)的边界条件同前文标准工况;线性分析(独立分析)的边界条件见图7,线性分析中货叉架原接触1的位置用X移动方向(UX)约束代替;原接触2位置用Z移动方向(UZ)约束代替;原链条位置用Y移动方向(UY)约束代替。整体约束关于OXY平面对称,其他条件设置同非线性分析中的条件设置(见表1和表2)。 (a)标准工况 (b)偏载工况 (c)举升工况图6 原始门架结构不同工况下位移云图Fig.6 The displacement cloud chart of the original door frame under different working conditions 图7 货叉架线性及非线性分析边界条件Fig.7 Boundary conditions of fork frame underlinear and nonlinear analysis 货叉架非线性及线性分析的结果见图8。从图8中可以看出,非线性及线性分析得到的货叉架最大应力分别为163.8 MPa和161.9 MPa,相对偏差为1.2%,在合理范围内;整体应力分布基本上是一致的,且最大应力均出现在货叉架滚轮板与下横梁焊接位置(见图8局部放大部位)。结果表明:非线性分析结果与线性分析结果是吻合的,非线性分析结果是准确的。 (a)非线性分析 (b)线性分析图8 货叉架非线性及线性分析应力云图Fig.8 The stress chart of fork frame under nonlinearand linear analysis 同时,非线性分析由于使用接触作为边界条件,会更加接近真实状态。对于零部件较多的结构,使用带接触的非线性分析虽然增加了计算机的计算量,但能显著减少分析人员的工作量,从而提高了工作效率。 在多工况拓扑优化或多目标拓扑优化领域,一直缺乏客观有效的工况权重系数分配方法。为此,笔者基于Miner准则(即疲劳损伤累积假说[18])及工况雷达图[19],依据工况数据,提出评估不同工况对门架损伤程度的工况风险评价方法及工况风险指标(risk index,RI)的概念;然后基于工况风险指标分配工况权重系数进行多工况拓扑优化,并与传统平均分配法得到的结果进行对比分析。基于工况风险评估的多工况拓扑优化流程见图9。 图9 基于工况风险评估的多工况拓扑优化流程Fig.9 Multi-working condition topology optimizationprocess based on working condition risk assessment 依据Miner法则[18],材料在一定应力水平下工作一段时间后会受到某种程度的损伤,当损伤累积到一定水平就会造成材料的疲劳破坏。由此可知,材料的疲劳损伤与其应力水平及工作时间有关,因此,本文提取应力及工作时长作为工况风险评估的2个特征参数。此外,门架结构在工作过程中会产生变形,若变形较大则会造成结构干涉或碰撞,对结构造成意外损伤。故在应力及工作时长的基础上,选取结构形变位移作为工况风险评估的第3个特征参数。 同时,为了准确地评估3个特征参数对结构的影响程度,选取最大应力比应力阈值、最大位移比位移阈值及工作时长所占比重,对工况特征应力、位移及工作时长分别进行归一化处理,并分别定义为应力指标IS(stress index,SI)、位移指标ID(displacement index,DI)、时长指标IT(time index,TI)。计算表达式分别如下: IS(i)=S(i)/ST (2) ID(i)=D(i)/DT (3) (4) 式中,S(i)、D(i)、T(i)分别为第i个工况的结构最大应力、最大位移及工作时长;ST、DT分别为结构的应力阈值和位移阈值。 为保证门架不发生塑性变形,取16Mn的屈服强度345 MPa为应力阈值;同时为保证门架的刚度满足工况的刚度要求,根据设计经验取位移阈值为5 mm。 通过对叉车某一作业流程进行监测,得到叉车在3种典型工况下的工作时长,根据式(4)计算各工况工作时长的占比,从而得到各工况时长指标数值,见表3。 表3 叉车某作业状态下工况时长及时长指标 此外,需要计算叉车门架在不同工况下的应力指标IS和位移指标ID。前文已进行门架结构在3种典型工况下的静力学有限元分析,得到门架在不同工况下的最大应力及最大位移,根据式(2)、式(3)分别计算工况应力指标IS及位移指标ID。通过归一化处理后得到的3种工况指标值见表4。 表4 叉车某作业状态下工况指标 雷达图是一种应用广泛的综合评价方法,其最鲜明的特点是可视化,能够直观地显示被评估对象的状态,同时可通过数值比例组合实现定量评价[19]。为了准确地评价3种工况指标对门架的综合损伤程度,根据表4中的数据,绘制工况风险单位面积雷达图(图10)。其中,以各工况在雷达图中所围多边形面积(工况雷达图面积)来评估不同工况对门架的损伤程度。 图10 工况风险雷达图Fig.10 Working condition risk radar chart 依据工况风险雷达图(图10),本文提出一种衡量不同工况相对重要程度的指标,定义为工况风险指标IR(risk index,RI),其表达式如下: (5) 式中,IR(i)为第i个工况的工况风险指标;Ai为第i个工况的工况雷达图面积。 通过MATLAB编程计算各工况的雷达图面积,并根据式(5)计算工况风险指标IR,结果见表5。工况风险指标IR越大,表明在该工况下工作门架的损伤风险越大(即该工况更为重要),因此,本文提出的基于工况风险指标IR的多工况拓扑优化权重系数分配方法更具客观性。 表5 工况雷达图面积及工况风险指标 (1)构建门架结构的拓扑优化模型。由第2节有限元分析结果可知:内门架的上下横梁及货叉架的两中梁的最大应力为231.2 MPa,远小于门架材料的屈服强度345 MPa,且多数区域的应力小于100 MPa,内门架横梁及货叉架中梁存在强度冗余,门架结构有轻量化设计的空间,因此,在内门架左右槽钢及货叉架上下梁之间进行材料填充并作为设计区域,构建门架结构的拓扑优化模型(图11)。 (a)背面 (b)正面图11 门架的拓扑优化模型Fig.11 Topology optimization model of door frame (2)采用带权重系数的折中规划法构建门架结构的多工况拓扑优化目标函数。根据式(1),取门架在3种工况下的工况风险指标IR=0.471,0.250,0.279,分别作为工况权重系数wi的值。将多工况刚度最大转换为单目标刚度最大问题,在ABAQUS的Optimization模块中设置目标函数,设置体积系数(设计变量状态下的结构有效体积与初始体积的比值)为0.2;同时,为了避免最终拓扑结构中出现细小的传力路径[20],保证结构具有较好的工艺性,设置最小拓扑尺寸为20 mm,最大拓扑尺寸为120 mm,设置对称几何约束。采用平均分配法作为对比,取3种载荷工况的权重系数均为0.333,其余条件保持不变来进行拓扑优化。 风险评估法及平均分配法分别经过27次和26次迭代后收敛,迭代过程见图12。从图12中可以看出,迭代过程中门架加权柔度不断减小,最终趋于稳定。其中,平均分配法得到的最终柔度为89 738.22 N/m;而风险评估法得到的最终柔度值为88 615.67 N/m,较平均分配法的最终柔度值小1 122.55 N/m,因此,相对于传统的平均分配法,风险评估法能得到更小的加权柔度值。 图12 拓扑优化迭代过程Fig.12 Iterative process of topology optimization 图13所示为门架拓扑优化结果,W1、W2分别为采用风险评估法和平均分配法得到的货叉架中梁最窄处宽度;H1、H2分别为采用风险评估法和平均分配法得到的焊接板(上部2个)高度方向长度。由图13可以看出,风险评估法和平均分配法得到的门架拓扑结构基本相同。内门架槽钢之间的横梁由原来较宽的2根变成不同尺寸呈一定距离排列的4根;货叉架的中梁由2根变为1根,并在原结构2根中梁的位置拓扑生成4个焊接板。整体结构在空间中呈平面对称分布。 (a)风险评估法 (b)平均分配法图13 拓扑优化结果Fig.13 Result of topology optimization 通过测量得到W1=35 mm,W2=25 mm;H1=30 mm,H2=40 mm。通常来说,尺寸越大,强度越高。W1>W2,表明在标准工况下,采用风险评估法得到的结构较平均分配法得到的结构,其强度更大;且风险评估法中标准工况的权重系数也更大(风险评估法中的权重系数为0.471,平均分配法中的权重系数为0.333)。两种方法中,工况权重系数大小与结构强度大小的规律一致,间接证明了拓扑优化结果的合理性。 综上可知,风险评估法相对于平均分配法在权重分配上更加合理有效,但是否有更优的工况权重分配方法需要进一步研究。 综合考虑门架在3种载荷工况下的性能,选取风险评估法得到的门架结构(加权柔度更小)作为设计参考。结合可加工性及加工经济性,采用三维软件SolidWorks对门架结构进行再设计,得到新的门架结构,见图14。新门架槽钢间4根横梁的宽度从上到下依次为60 mm、55 mm、65 mm、35 mm,原始门架的2根横梁宽度均为120 mm,对比可知新门架的总耗材量有所减少。货叉架中梁上下宽中间窄,宽处为75 mm,窄处为35 mm;焊接连接板轮廓呈类抛物线状。 (a)正面 (b)背面图14 新门架结构Fig.14 New structure of door frame 为了验证新门架结构的力学性能,建立新门架有限元模型,边界条件及载荷与第2节相同,分别在标准、偏载、举升3种典型工况下进行有限元分析,新门架结构在不同工况下的应力云图和位移云图分别见图15和见图16。由图15和图16可以看出,在3种工况下,新门架的最大应力分别为176.3 MPa、207.5 MPa、217.7 MPa;最大位移分别为4.109 mm、4.163 mm、4.120 mm。对比前后有限元分析结果可知: (a)标准工况 (b)偏载工况 (c)举升工况图15 新门架结构不同工况下应力云图Fig.15 The stress cloud chart of the new door frame under different working conditions (a)标准工况 (b)偏载工况 (c)举升工况图16 新门架结构不同工况下位移云图Fig.16 The displacement cloud chart of the new door frame under different working conditions (1)相对于原门架结构,优化后的门架结构在3种典型工况下的最大应力分别减小10.05%、10.25%和1.58%,最大位移分别减小13.17%、12.93%和8.28%,质量减小7 kg。新门架结构具有更高的强度及刚度,且质量更小。门架原始结构与新结构的对比数据见表6。 表6 门架原始结构与新结构强度及刚度对比 (2)标准工况下门架的最大位移减小最多,刚度提升最为显著,这与拓扑优化中标准工况的权重系数最大是一致的,一定程度上验证了基于工况风险评估的权重系数分配方法的合理性。 (1)通过对叉车门架系统的合理简化、准确的接触设置,实现叉车门架的整体非线性有限元分析,并与线性分析结果进行对比,验证了非线性分析结果的准确性,同时避免了工况多变需要反复分析计算边界条件而带来的繁琐。 (2)基于工况数据(工作时长、结构应力及形变位移),提出了工况风险评估方法及工况风险指标的概念,并据此提出一种分配多工况拓扑优化权重系数的方法,该方法较平均分配法在多工况拓扑优化中能得到更优的目标值,为工程实践中处理多工况优化权重系数分配问题提供了新的思路。 (3)结合折中规划法,实现叉车门架结构多工况拓扑优化,并根据优化结果对门架结构进行改进设计。新门架结构在不同工况下的强度及刚度均得到提升,且实现了减重,为设计性能更优的叉车门架结构提供了参考。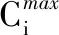
2 叉车门架的接触非线性有限元分析及准确性验证
2.1 叉车门架接触非线性有限元分析



2.2 准确性验证

3 工况风险评价方法及门架结构多工况拓扑优化

3.1 工况风险评价方法
3.2 叉车门架的多工况拓扑优化


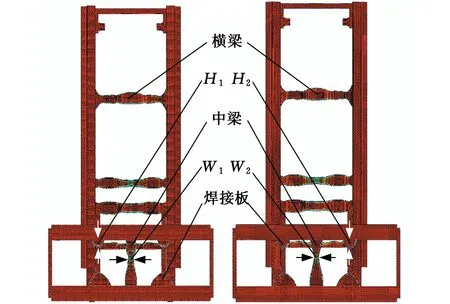
3.3 门架结构再设计及结果分析

4 结论

