安全容量限制下人群分类对应急疏散影响研究

李建光，赵寒青

(上海市地下空间设计研究总院有限公司，上海 200020)

地震、洪涝、台风、海啸、火灾、交通事故、化学核泄漏及恐怖袭击等事件频繁发生，使得人们的生命财产安全受到极大威胁。根据应急事件数据库(emergency events database，EM-DAT)数据，1980—2016年世界各地共发生了11 826起自然灾害，累计造成2 614 072人死亡，导致的经济损失高达28 110亿美元(http://www.emdat.be/)。突发灾害事故情况下的应急疏散决策是减少生命财产损失，特别是减少群死群伤事故发生的有效手段。

目前在灾害事故应急疏散方面，国内外学者进行了大量研究[1-4]。已有研究中的疏散模型主要可分为微观模型与宏观模型两大类。微观疏散模型以疏散个体为研究对象，通过模拟待疏散人员的行为和人的恐慌心理对疏散路径的选择等进行实验分析[5-7]。微观疏散模型又可以分为社会力模型、元胞自动机模型和概率模型等。宏观疏散模型主要以疏散群体为研究对象，假定群体中的个体具有无差异性，以最小化疏散时间为目标，相关的疏散模型与算法大多是基于图论中的网络优化思想而建立的[8-9]。如PEL等分析了不同待疏散人员信息与遵循行为对疏散时间的影响[10]。HELIOVAARA等从待疏散人员的利己行为与合作行为角度探讨了行为选择对疏散时间的影响，发现当疏散者表现出利己行为而不是合作行为时，整个人群的疏散时间更少[11]。然而，较少有文献从心理与生理(年龄、性别、健康状态)角度研究疏散决策问题。ZHENG等给出了在建立疏散模型时应考虑待疏散人员的心理与生理特征的建议，但并没有给出具体模型[12-13]。相比而言，ALIZADEH基于待疏散人员的心理特征建立了疏散模型，将心理特征作为一个参数，规划了一个动态元胞自动机模型[14]。WANG等则运用定性模拟方法研究了大规模应急疏散过程中待疏散人员的恐慌传播[15]。但是，以上相关研究缺乏从生理角度去分析疏散决策问题。此外，为了提供更合理与更实际可靠的应急疏散计划，相关研究已开始关注待疏散人员的个体特征(知识结构、疏散信息的掌握程度)对疏散决策的影响。如KINATEDER等研究了待疏散人员在交通事故中的自我疏散行为，通过实验发现，接受过类似疏散训练且阅读了解过相关疏散知识的人群具有更快的疏散行为反应[16]。PIRES提出了一种方法去评估突发灾害事故时待疏散人员的疏散认知行为[17]。KOBES等通过研究发现待疏散人员对疏散环境信息的掌握程度很大程度上影响其疏散路线的选择[18-19]。

以上研究主要集中考虑具有确定性疏散需求的单源点疏散问题，但是对于实际突发灾害事故情形时，具有不确定性疏散需求的多源点疏散问题则更具一般性[20]。同时，相关疏散宏观模型大多以整个群体作为研究对象，没有考虑疏散人群的差异性特点。而以个体为研究对象的微观模型又不能较好地反映和利用疏散区域内人群的共性，不利于制定整体疏散计划。此外，人群的基础信息(年龄、性别和健康状态等)、人群知识结构与突发灾害事故时人群的心理等因素都会影响到疏散安全与疏散计划。如VORST等从人群的年龄、性别、健康状态和知识经历等角度探讨了人群特点对疏散计划的影响，提出了将人群的生理、心理等因素纳入疏散模型的建议[21-22]。但目前这些因素对于提高疏散效率和优化疏散计划的影响并没有被完全揭示。

因此，笔者针对多源突发事故点的不确定性疏散需求，根据待疏散人员的年龄、性别、健康状况、知识结构与疏散信息的掌握程度，对待疏散人群进行分类，设置人群疏散优先权，结合源点疏散优先权，建立多阶段动态疏散混合整数规划模型，制定疏散人群路径。最后，通过疏散场景设计与仿真，分析人群分类疏散策略对疏散效率的影响。

1 问题与模型

笔者考虑两类疏散优先权：①人群疏散优先权，对生理特征、知识结构、疏散信息掌握程度相似的疏散个体进行分类，设定相同的疏散优先权；②源点疏散优先权，各源点发生的灾害严重程度不同，根据各源点的受灾程度设置疏散优先权。为了使疏散计划更好地反映各疏散路段的实时人流状况，避免路段的过度拥挤、踩踏等次生灾害的发生，笔者提出了基于离散时间的动态疏散模型，将疏散时间划分为时间段，并考虑路段、交叉口、安置点的安全容量限制[23]。

主要的研究假设有：①所有的待疏散人员能完全听从调度，按事先制定的疏散计划进行疏散；②路段容量与交叉口缓存容量受城市内部交通流实时影响而变化；③疏散过程中只容许交叉口有停留，不允许返回；④能够以概率形式估计事故源点在某一场景下需要疏散的人员数量；⑤待疏散人员的属性(生理特征、知识结构、信息掌握程度)能够有效得知。

1.1 符号定义

(1)集合。O={1,2,…,NO}为突发事故源点集合，o为其中一个源点，o∈O；I={1,2,…,NI}为路段交叉口集合，i为其中一个交叉口，i∈I；D={1,2,…,ND}为安置点集合，d为其中一个安置点，d∈D；P={1,2,…,NP}为疏散人群集合，p为其中一类人群，p∈P；S={1,2,…,NS}为场景集合，s为其中一个场景；T={1,2,…,NT}为时间段集合，s∈S，t为其中一个时间段，t∈T。

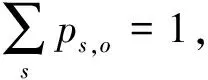
(3)决策变量。Rp为人群p已全部疏散到安置点的最迟时间；Qo,p为源点o的人群p全部疏散的时间；St,i,p为t时刻交叉口i滞留人群p的数量；Xt,j,p,h为t时刻从点j出发由经j与h之间路段的人群p数量，其中j∈(O∪I)，h∈(I∪D)；Yt,j,p,h为由经点j并在t时刻到达点h的人群p数量，其中j∈(O∪I)，h∈I；Zt,j,p,h∈{0,1}，在t时刻由经点j并经过j与h之间路段的人群p数量大于0时，其取值为1，否则取值为0，其中j∈(O∪I)，h∈(I∪D)。

1.2 模型

式(1)为目标函数，表示最小化疏散转移时间与等待疏散时间；式(2)表示迫使源点o的人群p全部被疏散；式(3)～式(7)表示如果某一路段不连通，则不能在该路段进行疏散；式(8)～式(11)表示某一时间段疏散进入该路段的人流量不能超过其容量限制；式(12)表示第t时间段由源点o疏散经过路段(o-i)的人群p的数量等于在第t+vo,i时间段到达交叉口i的人群p的数量；式(13)表示疏散人群必须经历路段(o-i)的疏散时间才能到达交叉口；式(14)表示第t时间段由交叉口i疏散经过路段(i-i*)的人群p数量等于在第(t+vi,i*)时间段到达交叉口i*的人群p的数量；式(15)表示疏散人群必须经历路段(i-i*)的疏散时间才能到达交叉口；式(16)表示第t时刻交叉口i滞留的人群p的数量；式(17)表示交叉口i滞留的人群数量必须小于等于其容量限制；式(18)～式(19)表示交叉口i的流量守恒关系；式(20)表示疏散到安置点d的人流总量不能超过其安置能力；式(21)表示疏散到安置点的总人群数量必须等于总疏散需求量；式(22)～式(27)表示各路段在第t时间段是否疏散人群p的关系；式(28)～式(29)表示人群p的疏散转移时间；式(30)～式(31)表示源点o人群p的等待疏散时间。

(1)

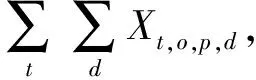
(2)

Xt,o,p,d≤M·lo,d,∀t,o,p,d

(3)

Xt,o,p,i≤M·lo,i,∀t,o,p,i

(4)

Xt,i,p,i*≤M·li,i*,∀t,i,p,i*≠i

(5)

Xt,i,p,d≤M·li,d,∀t,i,p,d

(6)

Xt,j,p,h≥0,∀t,p,j∈(O∪I),h∈(I∪D)

(7)

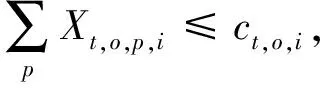
(8)

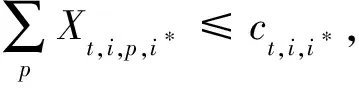
(9)

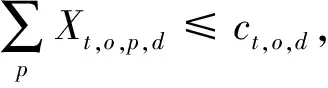
(10)

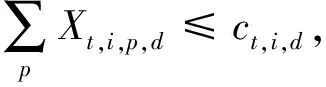
(11)

Yt*, o, p, i=Xt, o, p, i,∀t,o,p,i,t*=t+vo,i

(12)

Yt,o,p,i=0,∀t,o,p,i,t≤vo,i

(13)

Yt*,i,p,i*=Xt,i,p,i*,∀t,i,p,i*≠i,t*=t+vi,i*

(14)

Yt,i,p,i*=0,∀t,i,p,i*≠i,t≤vi,i*

(15)

∀t,i,p

(16)

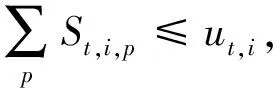
(17)

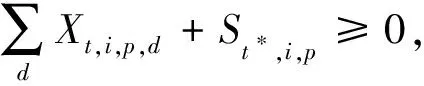
(18)

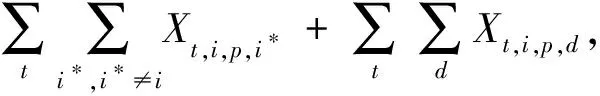
(19)

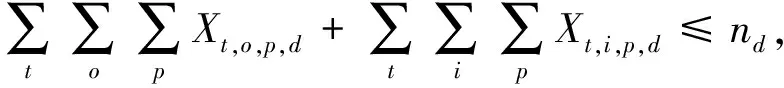
(20)

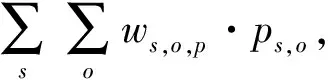
(21)

Xt,o,p,d≤M·Zt,o,p,d,∀t,o,p,d

(22)

Xt,o,p,d≥Zt,o,p,d,∀t,o,p,d

(23)

Xt,i,p,d≤M·Zt,i,p,d,∀t,i,p,d

(24)

Xt,i,p,d≥Zt,i,p,d,∀t,i,p,d

(25)

Xt,o,p,i≤M·Zt,o,p,i,∀t,o,p,i

(26)

Xt,o,p,i≥Zt,o,p,i,∀t,o,p,i

(27)

Rp≥Zt,o,p,d·(t+vo,d),∀t,o,p,d

(28)

Rp≥Zt,i,p,d·(t+vi,d),∀t,i,p,d

(29)

Qo,p≥Zt,o,p,i·t,∀t,o,p,i

(30)

Qo,p≥Zt,o,p,d·t,∀t,o,p,d

(31)

2 仿真算例

2.1 参数设置

疏散网络如图1所示，其中各边上括号中的第一个数值为该路段的最大容量，第二个数值为通过该路段的疏散时间。交叉点具有一定的缓存容量：ut,i～U[3,6],∀t,i；安置点1能够接纳疏散总人数的55%，安置点2能够接纳疏散总人数的45%。考虑3种场景：①源点轻度受灾，影响范围较小，待疏散人数较少；②源点受灾较严重，影响范围较大，待疏散人数较多；③源点严重受灾，影响范围大，待疏散人数急剧增加。场景概率ps,o在区间[0,1]内随机取值，各源点在3种场景下的待疏散人员数量分别在区间[6,10]、[10,14]与 [14,20]内随机取值。

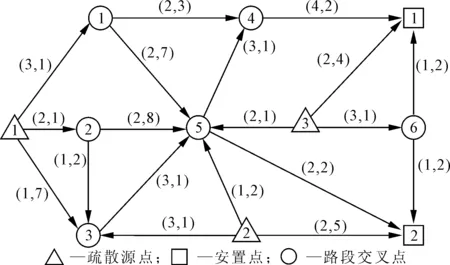
图1 疏散网络

将待疏散人员分为具有不同优先权的3类人群：①将老弱病残者、文化程度较低者、年幼者及大部分女性定义为待疏散人群Ⅰ，其疏散需求量占总疏散需求的30%；②将文化程度较高、未经历过类似应急疏散，同时信息掌握不完全者定义为待疏散人群Ⅱ，其疏散需求量占总疏散需求的50%；③将文化程度高、地理环境信息、导向信息等掌握较完全，并经历过类似应急疏散或培训的人员定义为待疏散人群Ⅲ，其疏散需求量占总疏散需求的20%。待疏散人群Ⅰ的优先权大于待疏散人群Ⅱ，待疏散人群Ⅱ的优先权大于待疏散人群Ⅲ，即设定eⅠ、eⅡ与eⅢ分别为4、2与1。同时，设定g1、g2与g3分别为4、2与1。笔者采用优化软件CPLEX 12.2 求解式(1)～式(31)，分析人群分类对疏散效率影响。

2.2 结果分析

2.2.1 疏散路线

在动态疏散过程中，首先由疏散源点将待疏散人员分配给交叉口或直接疏散给安置点；然后，交叉口根据到达的人流情况将人员疏散给下一交叉口或安置点，以此逐层疏散分配，直到所有被疏散人员到达安置点为止。疏散线路如表1所示。由表1可知，人群Ⅰ在t=7时刻全部疏散至安置点，人群Ⅱ在t=10时刻全部疏散至安置点，人群Ⅲ在t=9时刻全部疏散至安置点。

2.2.2 人群分类对疏散效率影响分析

为分析疏散优先权对疏散的影响，通过式(32)将疏散平均时间的倒数定义为疏散效率(EF)：

(32)

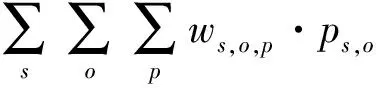
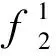
表1 疏散线路

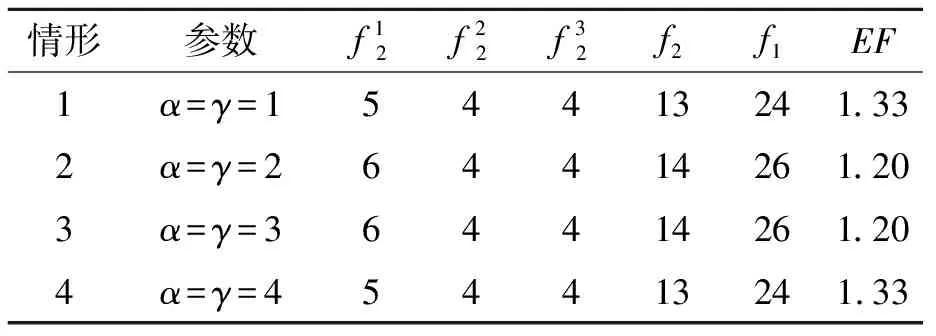
表2 源点疏散优先权对疏散效率影响结果

(2)人群疏散优先权对疏散效率影响分析。设定α=γ=2，调整β和δ的取值，分析人群疏散优先权对疏散效率的影响，具体结果如表3所示。由表3可知，随着β、δ值的增大，平均疏散时间增大，疏散效率下降近10%，最后趋于不变。这是因为随着β、δ值的增大，在目标函数值最小化的驱使下，疏散计划将根据疏散优先权的大小依次疏散相应人群，使得具有低疏散需求量和低疏散优先权的人群等待疏散的时间显著增加。例如，采取情形2的疏散策略时，源点1的人群Ⅰ的等待疏散时间为1，人群Ⅱ的等待疏散时间为2，人群Ⅲ的等待疏散时间为3；而采用情形1的疏散策略时，人群Ⅰ、Ⅱ和Ⅲ的等待疏散时间则分别变为1、3和1。这表明在制定疏散策略时，如果根据人群特点一味追求人群差异化疏散，势必影响整体的疏散效率。

表3 人群疏散优先权对疏散效率影响结果

如果调整人群疏散优先权，如在情形5中增大人群Ⅱ的优先权，则明显改变整个疏散计划的疏散效率。尤其当疏散人群需求量基数较大时，其影响更为明显，如人群Ⅱ。此外，源点疏散优先权调整的影响往往更具全局性，如情形6。因此，制定疏散策略时应该综合考虑人群差异特点与源点受灾程度，以确定人群疏散优先权与源点疏散优先权之间的最优组合关系。同时，疏散优先权的制定也要兼顾待疏散人群的疏散需求量，以不影响整体的疏散效率。

(3)安全容量限制对疏散效率影响分析。考虑到城区路段与交叉口的容量一般会受到城市固有交通流的影响，设定ct,o,i与ct,i,d～U[0,4]，ct,i,i*与ct,o,d～U[2,4]，分析安全容量限制变化对疏散效率的影响，具体结果如表4所示。由表4可知，相对于不具有缓存容量的情形，交叉口具有缓存容量的情形的等待疏散时间能够明显减少，疏散效率明显提高。因此，建议在相应路段增设一些临时缓存点(被疏散人员可以短暂停留的点)。临时缓存点可以缓解后面疏散路段的压力，提高疏散效率的同时也会很大程度地减少被疏散人员的等待时间。此外，路段容量的实时变化给疏散计划的制定增加了难度，相比固定容量情形，路段平均容量随时间减少的情形明显降低了疏散效率；而随着路段平均容量的增大，疏散效率明显提高。因此，为了有效提高疏散效率，在制定疏散计划时要充分考虑各路段的实际通行能力，并充分利用临时缓存点的缓存功能，尽量避免城市内交通流高峰路段。

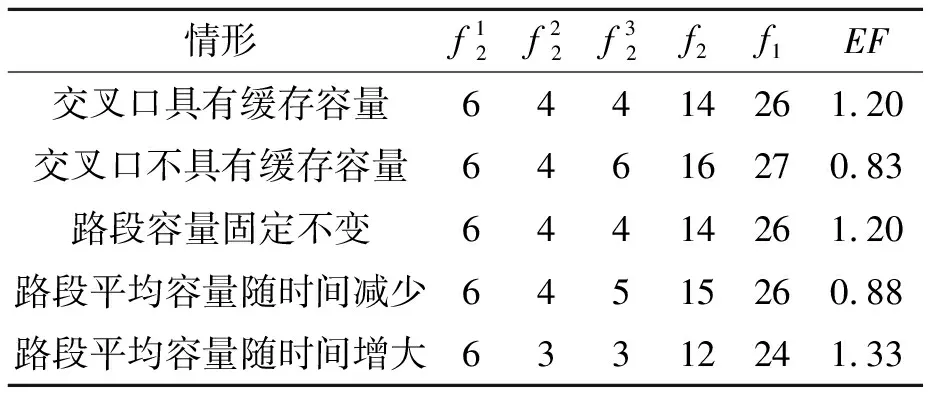
表4 安全容量对疏散效率影响结果

3 结论

笔者针对多源点突发灾害事故时人群分类对安全容量限制的应急疏散计划影响问题，从待疏散人员的年龄、性别、健康状态、知识结构与对疏散信息的掌握程度等角度对待疏散人群分类，确定人群的疏散优先权，实行差异化疏散。考虑不确定性疏散需求和安全流量，建立了动态疏散的混合整数规划模型，为网络流量调整策略设计提供工具。通过仿真算例发现，疏散优先权的制定既要考虑人群所具有的差异性，又要兼顾待疏散人群的疏散需求量，以优化疏散效率；在交叉口设置临时缓存点，不仅能提高疏散效率，还能降低疏散人员的等待时间。