混合装配线平衡中的工效学和装配空间联合优化研究
蔡敏,黄刚,汪挺,沈琼玮
( 杭州电子科技大学 工业工程与管理研究所,杭州 310018 )
1 引言
混合装配线平衡问题(MMixed-Model Assembly Line Balancing Problem,简称 MALB-P)是指在满足作业任务的优先级关系约束和节拍时间约束的情况下,将作业任务通过合理的组合,均衡地分配给各工位的过程[1~3]。混合装配线具有柔性系统的特性、能快速响应不断变化的客户个性化需求,但混合装配线的产品种类、作业任务的复杂程度和操作者的作业负荷要高于单一产品装配线。一方面,过度的工效学负荷不仅会降低操作者的生产效率,且极易引发肌肉骨骼疾病(Musculo-Skeletal Disorder,简称 MSDs)[4];另一方面,产品种类增加会导致装配线边库存成本急剧上升,在进行装配线的平衡设计时,平衡方案决定了各工位的线边库存水平。因此,在进行装配线的平衡优化时,必须综合考虑工效学和空间约束,使混合装配线在平稳生产的前提下,降低操作者作业负荷和线边库存成本,帮助制造企业朝着高效和人性化生产的方向发展。
装配线平衡(Assembly Line Balance,ALB)的概念最早是由美国学者布莱顿于1954年在他的硕士论文“连续装配线平衡”中首次提出[5]。此后,许多国内外的研究学者基于实际生产情况,从不同的角度出发构建了更契合实际生产活动装配线平衡模型,大大提高了制造企业的生产效率和经济效益。Bautista等[6]将时间和空间因素纳入SALBP,构建了考虑装配空间约束的装配线平衡模型(Time and Space constrained Assembly Line Balancing Problem, TSALBP),认为在进行装配线平衡时,不仅要满足时间约束和优先关系约束,并且各工位上的物料和设备占用的空间大小不能超过最大可用装配空间大小。Otto等[7]将操作者的工效学风险纳入SALBP模型中。Bautista等[8-9]在此基础上定义了TSALBP-ergo模型,分析了操作者可接受的最大风险对工位数量的影响,并通过混合整数线性规划来寻求最小化站点的最大人体工程学风险的方案。但这些研究大都是以传统简单装配线为研究对象,并且采用传统工效学评估方法评估操作者的工效学风险,但传统的工效学评估方法大都采用定性或半定量的方式,很难将工效学目标纳入MALB-P模型的目标函数中,Battini等[10-11]引入了预定动作能耗系统来快速估计操作者的能量消耗,但没有考虑空间约束问题,也没有对混合装配线中操作者的能量消耗问题进行研究。因此,本文以最小化工位个数和平滑指数为目标,即针对第1类混合装配线平衡的工效学和装配空间问题进行了研究,构建了混合装配线平衡的工效学和装配空间联合优化模型。
2问题描述与假设
2.1 问题描述
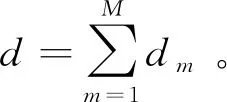
考虑工效学和空间约束第1类混合装配线问题有以下几个假设:
(1)装配线的节拍时间、各作业任务的作业时间、所需物料占用的空间大小和所需能量消耗量以及装配线相关信息都已知;
(2)各作业任务时间tjm之间是相互独立,不考虑操作者对作业时间的影响;
(3)不考虑产品投产排序,且混合装配生产的产品投产比例已知。
2.2 模型相关参数说明
模型相关参数如下:
K表示所需工位的数量上限;
I表示作业元素的集合I={1,2...,N};
aj表示作业任务j的物料所需的物料空间大小;
xjk表示当作业任务分配到工位K时,其值为1,否则值为零;
S表示装配线的工位数量;
SI表示装配线的平衡指数;
Tk表示分配给工位k的作业任务总时间;
Tmk表示分配到工位k的第m种产品的作业任务时间;
Emk表示分配到工位k的第m种产品的作业任务的能量消耗量;
Ek表示完成分配给工位k的作业任务所需的能量消耗量;
(Ek表示完成分配给工位k的作业任务的平均能量消耗率;
RAk表示完成分配给工位k的作业任务的宽放系数;

3 模型构建
本文研究的第1类混合装配线平衡的工效学和装配空间的联合优化问题,即给定生产节拍c,求满足约束条件下的最小化工位数。根据上节描述,可建立第1类混合装配线平衡的工效学和装配空间的联合优化问题的模型如下[13~16]:
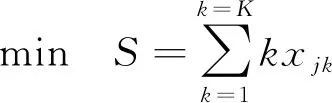
(1)
平衡指数是评估平衡优化效果的重要指标,平衡指数越小,各工位的负荷越均衡。

(2)
因此在进行装配线平衡时,为了获得更好的平衡优化效果,构造目标函数如下:
(3)

(4)
优先级约束:
(5)
工位空间约束:
(6)
单位周期内M种产品的第j个零件的空间:
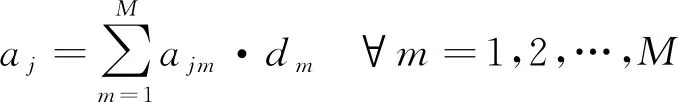
(7)
分配到工位k上的第m种产品的作业任务时间:
(8)
工位k的作业任务的任务总时间不超过节拍时间:
(9)
为了降低装配线上操作者的MSDs风险,研究者已经开发了多种评估MMH风险值的方法。如NIOSH提举方程,OWAS方法和欧洲装配工作表。NIOSH提举方程或OWAS指数,只适用于评估执行特定任务的半定量风险指数,对于在不同的作业姿势的评估有一定的局限性,如NIOSH提举方程仅计算提升任务的瞬时推荐重量限制,而OWAS是非常严格的制定重量限制,很难运用于一个优化模型的目标函数。为了在装配线平衡模型中考虑工效学因素,Garg等[17-19]开发了一种能快速估算能量消耗率的方法,能量消耗率是维持不同的身体姿势(如坐,站立,弯腰)和动作(如举起,放下、搬运、握持)所需总能量与执行任务所需总时间的比值,能量消耗率受性别、体重、负荷大小、提举的垂直高度、搬运距离、搬运过程行走的速度、工作的姿势和持续时间的影响。对于给定任务i,完成该任务的平均能量消耗率可以表述为:
(10)

分配到工位k上的第m种产品的作业任务的能量消耗量:

(11)
完成分配到工位k的作业任务所需的能量消耗量:
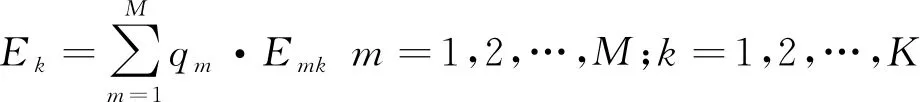
(12)
完成分配到工位k的作业任务的能量消耗指数:
(13)
完成分配到工位k的作业任务的宽放系数:

(14)
考虑工效学后工位k作业任务的时间:
(15)
(16)
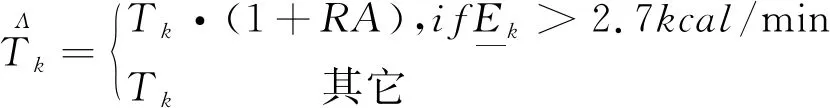
(17)
考虑工效学因素的节拍约束:
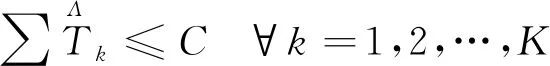
(18)
4 算法设计
第1类混合装配线平衡的工效学和装配空间的联合优化问题是典型的组合优化问题。因此,本文的求解算法可采用遗传算法,使用遗传算法求解考虑工效学和空间约束的混合装配线平衡问题时的流程图如图1所示。
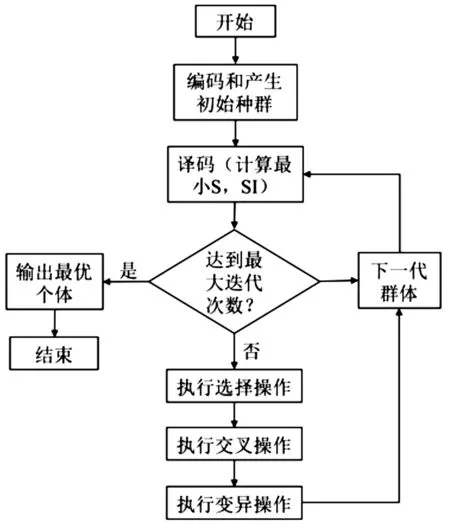
图1 遗传算法流程
4.1 编码和产生初始种群
初始种群由若干个体编码组成。初始种群产生的思路是:(1)随机产生一个满足约束的解;(2)对该解编码,其步骤如下:
步骤1 设个体计数器count=1
步骤2 可行解的产生:
(1)作业任务的集合TK={tk1,tk2,…tkN};
(2)集合PK表示在集合TK中没有紧前任务的作业任务;
(3)假设k为工位编号,k∈(1,2,…K),初始化第一个工位ktk=kt1;
(4)随机从集合PK中选择一个作业任务akj(akj∈PK)分配给当前工位ktk;
(5)同时判断当前工位考虑工效学因素后的作业时间是否超过节拍时间c、所需物料占用空间大小是否超过装配空间A,若其中某项超过,则需重新进行作业任务的分配,转(7);否则转(4);
(6)删除TK中的作业元素akj,并重新统计集合PK,然后转至(5);
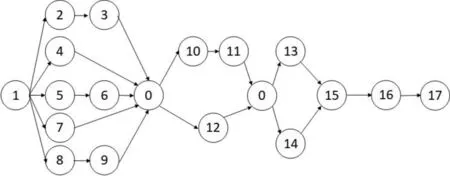
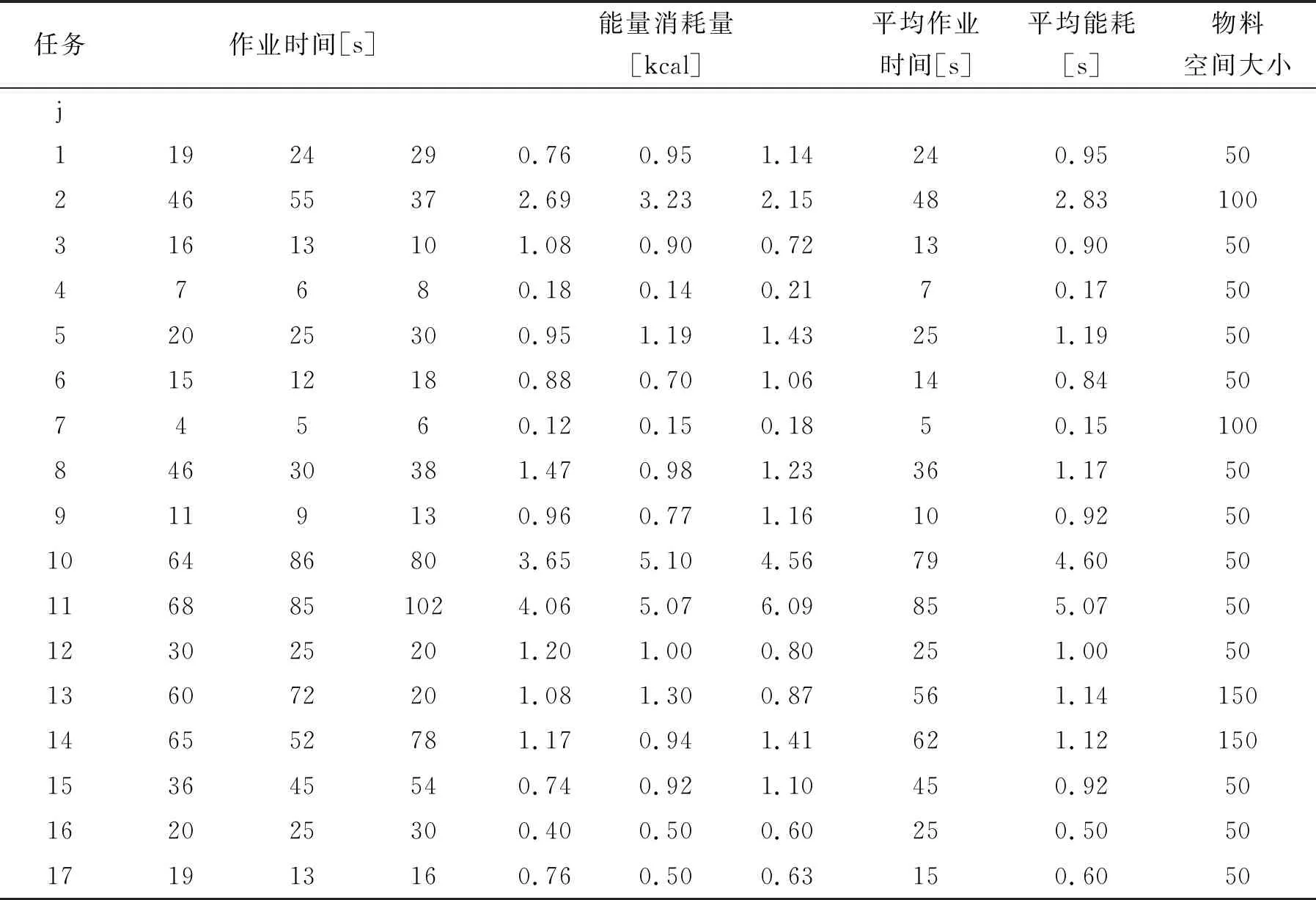
(7)K=k+1,如果s (8)把未分配的任务安排到工位ktN; (9)检查最后一个工位ktN考虑工效学因素后的作业时间是否超过节拍c、所需物料占用空间大小是否超过装配空间A,若都没有超过,转至步骤三;否则,转至步骤2。 步骤3 编码步骤2中产生的可行解。 步骤4 若co+1 ≤ top_size,co =co+1,转步骤2,否则转步骤5。 步骤5 结束 译码是指根据基因编码后的操作顺序,将作业任务依次分配到各工位上的过程。首先在满足考虑工效学因素后的作业时间不超过节拍c、所需物料占用空间大小不超过装配空间A等条件下,根据编码过程中的作业任务顺序,运用贪心算法把尽量多的作业任务放置在同一工位,并根据作业任务的划分求出各工位作业时间、所需工位数量和平衡指数,译码过程如图2所示。 图2 编码、译码示意图 为了更好地保留父代基因中的有效部分,本文采用次序交叉法进行交叉操作,即任意选取在选择操作过程产生的新种群中选取两个个体染色体,随机生成一个叉点,过程如下: 第1步:随机产生交叉点。 第2步:进行交叉,选取父代1交叉点左侧部分染色体进入子代1 。 第3步:根据父代2生成子代1染色体。 第4步:交换父代位置,产生子代2。 变异和交叉都是遗传算法的辅助性搜索操作,其目的是为了维持算法在寻优过程中种群的多样性。本文通过使用随机产生的一个新的染色体去替代满足变异概率条件下的原染色体。 在遗传算法中,适应度函数值一般为正,数值较大适应度函数可以提高进入下一代的染色体越的概率和优良性,本文结合范维博等[21]的研究,构造适应度函数如下: f(i)=0.9λS+SI (18) 其中SI为平衡指数,S为最小工位数。由于目标函数是小于1的幂函数的指数,目标函数越小,适应度函数越大,此时可获得最小工位数量和最小平衡指数。 常用的选择操作方法有轮盘赌选择法,然而,在进行选择操作时无法判断在迭代过程中进入下一代的个体是否都是比较优良的,这种缺陷可能会导致新种群的退化,而通过结合最优个体保留策略即可确保进入下一代的种群都是比较优良的。因此,本文的选择操作结合这两种相结合的方法,弥补了其各自的优缺点。 某制造企业中的一条混合装配线需要同时对三种结构相似、工艺相近、比例为1:2:1的产品A、B和C进行装配。混合装配线的生产节拍为173 s,产品的综合作业任务优先约束关系如图3所示(其中任务0为虚任务不占用时间和装配空间),每个任务作业时间和所需物料占用的空间大小数据见表1,各工站的最大可用空间大小为300,tjA、tjB和tjC分别表示不同型号的产品A、B和C第j个任务的作业时间;tj表示不同型号的产品以需求比例为权值的加权平均值,通过加权处理将混合装配线平衡问题转化为简单装配线平衡问题。 图3 作业任务综合优先顺序关系图 表1 各作业任务的时间、能量消耗量和物料空间大小 注:此处的体积是量纲为1的量。 为了进一步分析作业任务的工效学约束和空间约束对线平衡优化过程的影响,本文设置了四组对比实验,即方案一:不考虑工效学约束和空间约束的装配线平衡方案;方案二:考虑工效学约束的装配线平衡方案;方案三:考虑空间约束的装配线平衡方案;方案四:考虑工效学约束和空间约束的集成优化方案。首先,本文根据工位数量、节拍时间、平衡指数、空间利用率、能量消耗率等指标进一步的分析了各方案之间的差异。其次,按照上一节中介绍的启发式算法,利用MatlabR2014a软件编写了遗传算法的程序,其中的基本参数设置如下:假设初始种群大小为200,适应度函数中的λ值为0.02,交叉概率和变异概率分别设定为0.7和0.2。各方案的仿真结果如表2、3、4、5所示: 如表2所示方案一中,在不考虑工效学和空间约束的情况下,最小工位数量为4、平衡指数为58.78。工位1和2上操作者的平均能量消耗率超过工效学上限,如果操作者长期处于高负荷的状态,必会损害其身心健康和导致人因失误概率增加,因此,有必要为负荷较高的工位提供宽放时间,降低操作者的累积疲劳,但工位2上考虑工效学因素的作业时间超出节拍大小。另一方面,工位1物料所需空间大小为452,超过了最大可用空间大小。因此,有必要综合考虑工效学和空间约束,寻找新的平衡方案。 表2 方案一:传统装配线平衡问题结果分析 表3 方案二:考虑工效学的平衡方案结果分析 表4 方案三:考虑空间约束的平衡方案结果分析 方案二、方案三均仅考虑单一约束对装配线平衡的影响。如表3所示,方案二在只考虑工效学约束的情况下,最小工位数量为4。相比较于方案一,装配线的平衡指数由47.63下降到27.26,同时降低了操作者的工效学负荷,各工位的作业时间均未超过节拍时间。然而,由于方案二没有考虑物料的空间需求,工位1的物料空间大小超出装配空间限制,提高了生产线的库存成本。如表4所示,方案三在只考虑装配空间约束的情况下,最小工位数量和平衡指数分别为4和59.09,各工位物料空间大小均未超出装配空间限制。相较于方案一,整个生产线的空间利用率显著提升,但工位2上操作者的能量消耗率水平超出了可接受的工效学水平,考虑工效学因素后工位2的作业时间超出了节拍时间,会造成生产过程中装配线的堵塞,需要增加额外的工位。因此,应该在进行装配平衡的同时考虑工效学约束和空间约束。 如表5中方案四所示,在同时考虑工效学约束和空间约束的情况下,最小工位数量和平衡指数分别为4和70.26,平衡指数明显高于相较于方案一、二和三,但考虑工效学后的实际平衡指数远低于方案一和三、略高于方案二,这是因为方案二未考虑物料装配空间大小限制,而方案四中各工位的物料空间大小和操作者的能量消耗率均在可接受的范围内。 表5 方案四:联合优化方案结果分析 本节对以上所述四种方案进行对比与分析,各方案的最终结果如表6所示。 方案三、四考虑了作业任务的空间约束对线平衡优化过程的影响。当工站旁可用装配空间足够大时,作业任务的空间约束对线平衡优化过程的影响可以忽略不计,采用传统的线平衡方案更符合实际情况。然而,在实际情况中一般线边面积有限,工站周围无法放置过多的物料,同时线平衡优化的结果决定了各工站的所需物料的空间大小,一旦所需物料的空间大小超出了最大可用空间大小,会导致作业现场混乱、操作者作业空间不足,并最终影响操作者的作业效率和产品质量。因此,必须在进行线平衡优化的过程中考虑作业任务的空间约束对线平衡优化过程的影响。 方案二、四考虑了作业任务的工效学约束对线平衡优化过程的影响。在不考虑工效学约束的情况下,传统的线平衡优化方式有更低的平衡指数,但操作者的平均能量消耗率超出了可接受的工效学水平。在这种情况下考虑工效学后,瓶颈工序节拍时间均超出了生产节拍时间。对于考虑工效学约束的线平衡优化方式,尽管操作者的平均能量消耗率也超出了可接受的工效学水平,但瓶颈工序节拍时间均小于生产节拍时间,并且空间利用率有所提升。因此,必须在进行线平衡优化的过程中考虑作业任务的工效学约束对线平衡优化过程的影响。 相较于方案二、三只考虑了单一因素的影响,方案四同时考虑了两种因素对对线平衡优化过程的影响,考虑工效学后的瓶颈工序节拍时间均小于生产节拍时间,各工站所需物料的空间大小均小于最大可用空间大小,并且最大可用空间大小有所降低,极大地提高了空间利用率。 表6 各方案对比分析 混合装配线平衡问题中人的因素和装配空间约束等因素对整个装配系统的生产效率有很大的影响,但目前关于装配线平衡问题的研究很少有同时考虑这两种因素,本研究基于传统的MALB-P模型,考虑了工效学约束和空间约束对装配线平衡的影响,构建了第1类混合装配线平衡的工效学和装配空间的联合优化模型,利用遗传算法验证了模型有效性和实用性。但该模型没有考虑到操作者的姿态负荷和脑力负荷。事实上,由于操作者的个体差异,执行不同作业任务所需时间存在不同,每个操作者所能承受的体力和脑力负荷也存在差异。 未来的研究可以针对不同作业姿势下操作者的能量消耗率的测量、作业负荷脑力负荷的测量以及工作环境负荷评估等方面进行更深入的研究,以提高操作者的工作满意度和整个制造系统的效率。同时,考虑到装配空间限制和物料的配送与运输策略等因素的影响,使研究过程能够更加契合实际生产情况,研究成果能能更好的运用在实际生产中。4.2 译码

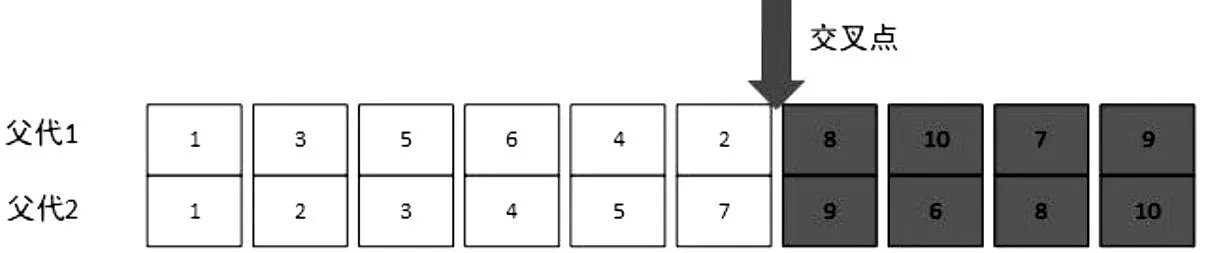
4.3 交叉与变异



4.4 构造适应度函数
4.5 选择操作
5 算例分析




6 讨论

7 总结

