美日欧中规范钢桥压杆稳定性计算对比研究

楚 得,郑凯锋,衡俊霖

(西南交通大学土木工程学院,成都 610031)

1 概述

随着我国基础设施建设和结构技术的快速发展，桥梁工程中钢结构的应用越来越广泛，其中各种钢桁架的弦杆和腹杆都是承受压力的杆件[1]。这类杆件截面尺寸小、细长，板件柔薄，在工程应用中易出现稳定问题，稳定承载力一般是其承载能力极限状态的控制因素[2]。故钢结构设计要足够重视稳定问题[3]。

在进行受压杆件的稳定设计时，需要同时考虑杆件的整体稳定性[4-7]和板件的局部稳定性[8-10]。针对板件的受力性能特点和板件在构件中所起的作用，有两种不同的处理方法：一种是保证板的屈曲荷载不低于构件的极限荷载，即保证构件在整体失稳前不发生局部失稳；另一种是允许板件出现局部屈曲，计算中计入屈曲后承载力。其中，第一种方法较为保守，所设计的杆件安全储备大，在设计时仅需限制板件的宽厚比，设计思想较为简单。但对于荷载较大、幅面尺寸较大的受压构件，采用第二种方法可以很好地避免钢材浪费[11]，获得较好的经济效益[12]。

目前大多数规范采用第二种方法进行稳定设计，即计入板件的屈曲后承载力。针对整体稳定问题，美国、日本、欧洲、中国的4种钢结构桥梁设计规范基于不同理论和试验数据，给出了不同的屈曲曲线以计算整体稳定折减系数。与此同时，欧洲、中国规范通过对板件截面进行折减来考虑局部稳定的影响，而美国、日本规范则对屈服强度或容许应力进行折减。

钢结构桥梁中常采用焊接H形截面杆件，在稳定设计中较具代表性。本文以此类型的受压构件为背景，介绍各国规范整体稳定和局部稳定的相关设计方法，并进行对比分析，以期为国内钢桥设计提供参考。

2 各国规范稳定设计方法

钢结构桥梁中的受压杆件通常同时承受轴向压力和弯矩的作用，属于压弯构件。美国、日本、欧洲、中国四种规范中分别给出了压弯构件的稳定验算式，可概括为统一的形式，如式(1)所示。此处，构件的长度方向定义为x轴，横截面平面为y-z平面。

f(N)+g(My)+h(Mz)≤1

(1)

式中f(N)——与轴向压力相关的验算式；

g(My)——与x-y平面弯矩相关的验算式；

h(Mz)——与x-z平面弯矩相关的验算式。

钢桥中的压弯杆件在承受荷载时，较轴向压力而言，弯矩往往属于次要作用[13]。式(1)中与轴向压力相关的第一项f(N)的数值远大于与弯矩相关的后两项g(My)和h(Mz)的数值，故本文仅讨论稳定验算式中的第一项f(N)。

f(N)中包含构件弯曲屈曲模态对应的构件整体稳定折减系数和板件局部稳定折减系数。为方便讨论及对比，将各国规范中的整体稳定折减系数统一用χ表示，局部稳定折减系数用ρ表示。下面分别进行介绍。

2.1 美国规范(AASHTO)

根据压弯构件所承受的轴向压力和构件轴压抗力之间的大小关系，美国规范给出了两个不同的稳定验算式[14]，其中与轴向压力相关的第一项f(N)不完全相同。f(N)如式(2a)所示。

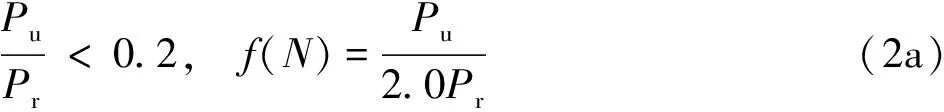
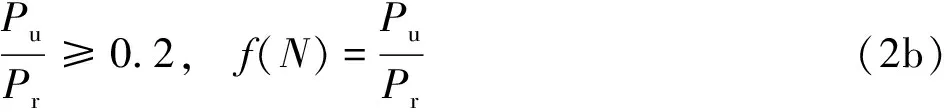
式中Pu——轴向压力设计值；

Pr——轴压抗力设计值，按式(3)计算。

Pr=φcPn

(3)

式中，Pn为名义受压抗力，应取弯曲屈曲、扭转屈曲和弯扭屈曲3种模态的最小值；单轴、双轴对称的截面，通常可取弯曲屈曲模态对应的受压抗力；φc为受压抗力系数，取0.90。

(4)

其中Po=QFyAg

式中Po——名义等效屈服荷载；

Pe——弹性临界屈曲荷载；

ρ——板件局部稳定折减系数；

Ag——构件横截面的毛面积；

Fy、E——钢材的屈服强度、弹性模量；

Kl/rs——构件的长细比；

K——有效长度系数；

l、rs——构件长度、回转半径。

(5)

令上式中的板件局部稳定折减系数ρ=1.0，即可得到美国规范所采用的整体稳定折减系数计算公式，如式(6)所示。

(6)

上式即为美国钢结构协会(AISC)对轴心受压柱稳定系数所采用的单条曲线。该曲线考虑了计算长度系数和初弯曲幅值，曲线由弹性状态过渡到弹塑性状态，稳定系数采用两个不同的曲线公式[12]。

通过设置宽厚比界限，美国规范界定了非长细构件和长细构件两种类别。其中，非长细构件的折减系数ρ=1.0，即不考虑折减。长细构件中，若只包含单边支承板元，其折减系数为ρ=ρs；若只包含双边支承板元，折减系数为ρ=ρa，若同时包含单边支承和双边支承板元，折减系数为ρ=ρs·ρa。

对于单边支承板元

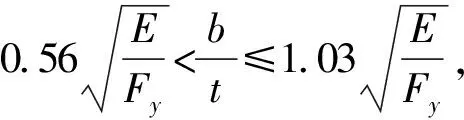
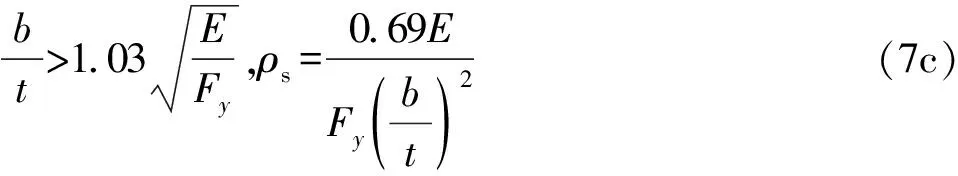
对于双边支承板元

(8)

式中，A为横截面的毛面积；Aeff为有效面积，Aeff=A-∑(b-be)t，需求出be。

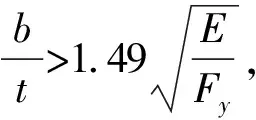
式中，f为构件的极限应力，f=ρsFy，为方便计算可取ρs=1.0。

对于单边支承板元

(10)

对于双边支承板元

(11)

2.2 日本规范(道路桥示方书)

与欧洲、中国、美国规范不同，日本规范以应力的形式给出了压弯构件的稳定验算式，与轴向压力相关的第一项f(N)如式(12)所示[15]。

(12)

σca=σcag·σcal/σcao

(13)

式中σc——轴力作用产生的截面压应力；

σca——轴心受压容许应力；

σcag——考虑整体稳定影响的轴心受压容许应力；

σcal——考虑局部稳定影响的轴心受压容许应力；

σcao——轴心受压容许应力的上限值。

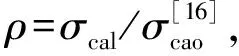
φ=χ×ρ

(14)

根据考虑残余应力、初始弯曲、截面类型的多条试验曲线，日本规范给出了计算整体稳定折减系数χ的经验公式，如式(15)所示。

(15)

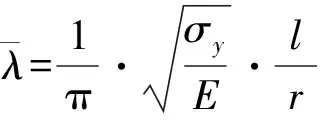
σy、E——钢材的屈服强度、弹性模量；

l、r——构件的长度、回转半径。

局部稳定折减系数ρ按公式(16)计算。

(16)

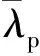
b、t——板件宽度及厚度；

ν——钢材的泊松比；

k——屈曲系数，双边支承板件取4.0，单边支承板件取0.43。

2.3 欧洲规范(Eurocode 3)

欧洲规范BS EN 1993-1-1中根据受压部分的宽厚比，将横截面分为4类，其中可应用于焊接桥梁结构的第Ⅳ类横截面具有以下特征：板件在屈服之前将出现局部屈曲[17]。对于仅受压的焊接H形截面，若满足如式(17)、式(18)所示的条件，则视为第Ⅳ类截面[18]。

腹板宽厚比

(17)

翼缘宽厚比

(18)

第Ⅳ类截面压弯稳定验算中轴压相关项f(N)如式(19)和式(20)所示。

(19)

NRk=fyAeff

(20)

式中χ——弯曲屈曲整体稳定折减系数；

γM1——构件稳定抗力的分项系数，取1.0；

NEd——轴向压力设计值；

NRk——轴压抗力特性值；

fy——钢材的屈服强度；

Aeff——考虑局部稳定影响的有效面积。

欧洲钢结构协会(ECCS)通过计入残余应力、初弯曲，在试验基础上按极限荷载理论得到了5条整体稳定曲线。基于此，结合Perry-Roberson公式[12]，欧洲规范BS EN 1993-1-1中给出了整体稳定折减系数χ的计算方法，如式(21)～ 式(23)所示。

(21)

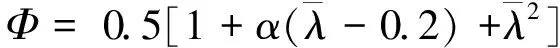
(22)

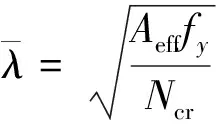
(23)

Ncr——基于毛截面特性的构件整体稳定弹性临界力；

α——缺陷系数，按表1取值。

表1 屈曲曲线的缺陷系数

对于板屈曲后强度的利用，Von Karman等提出了有效宽度的概念，Winter等根据试验建立了有效截面法设计公式[12]。在此基础上，欧洲规范BS EN 1993-1-5给出了有效面积Aeff=ρAc的计算方法，其中ρ为局部稳定折减系数[19]。特别地，考虑到Winter试验数据中单边支承单元的屈曲系数偏于保守，欧洲规范在应用Winter公式的基础上提高了折减系数ρ[20]。

对于双边支承单元

(24)

其中(3+ψ)≥0。

对于单边支承单元

(25)

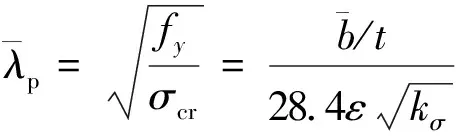
(26)

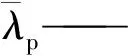
ψ——受压板件的应力分布比，对于轴心受压构件，ψ=1；

kσ——与应力比ψ和边界条件相关的屈曲系数，ψ=1时，双边支承板件kσ=4，单边支承板件kσ=0.43。

2.4 中国公路钢结构桥梁设计规范(JTG D64—2015)

在进行压弯杆件的稳定验算时，中国公路钢结构桥梁设计规范(以下简称中国规范)针对弯矩仅作用在一个对称轴平面和弯矩作用在两个主平面内两种情况，分别给出了不同的压弯构件稳定验算式，但式中与轴向压力相关的第一项f(N)均相同，如式(27)和式(28)所示[21]。

(27)

NRd=Aefffd

(28)

式中γ0——结构重要性系数；

Nd——构件中间1/3范围内的最大轴心压力设计值；

χ——轴心受压构件弯曲失稳模态的整体稳定折减系数；

Aeff——考虑局部稳定的有效截面面积；

fd——钢材的强度设计值。

在钢桥的稳定设计问题上，中国规范参考了大量的受压构件整体稳定和板件局部稳定试验。根据试验结果，板件不发生局部失稳时，轴心受压构件的整体稳定极限承载力可以用Perry公式近似表达。中国规范给出了整体稳定折减系数χ的计算方法，如式(29)和式(30)所示。

(29)

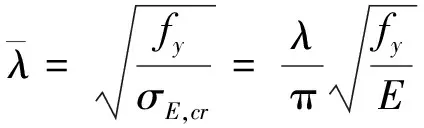
(30)

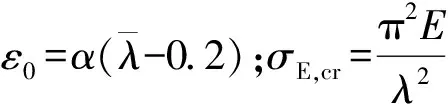
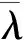
表2 整体稳定折减系数的计算参数α

在制定屈曲曲线时，中国规范参考了欧洲规范的相关规定，共分为a、b、c、d四条，缺少a0曲线。对比表1和表2，可以看出两种规范中对应屈曲曲线的计算参数非常接近。

Perry公式中的稳定系数以截面的边缘屈服为准则，中国规范中则是先按极限承载力理论确定出构件的稳定极限承载力后，再反算出ε0。此时ε0不仅与构件的初弯曲有关，而且综合了多种截面，为等效偏心率[12]。

与欧洲规范相同，中国规范在计算有效面积Aeff，c时也采用了Von Karman有效宽度的概念。不同的是，局部稳定折减系数ρ是以宽厚比为参数运用Perry公式进行计算。在计算有效截面面积Aeff，c时，需对被腹板或刚性加劲肋分割形成的若干板件分别进行计算，然后再求和得到整个横截面的有效面积。计算方法如式(31)、式(32)所示。

(31)

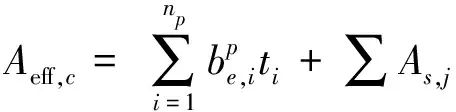
(32)

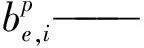
bi、ti——第i块受压板件的宽度、厚度；

np——被腹板或刚性加劲肋分割形成的受压板件数量；

∑As，j——有效宽度范围内的加劲肋面积之和；

ρi——第i块受压板件的局部稳定折减系数，按式(33)～ 式(35)计算。

(33)

(34)

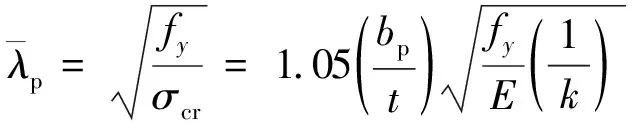
(35)

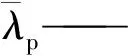
t——加劲板的母板厚度；

fy、E——钢材的屈服强度、弹性模量；

σcr——加劲板弹性屈曲欧拉应力；

bp——加劲板局部稳定计算宽度；

k——加劲板弹性屈曲系数，双边支承板件k=4，单边支承板件k=0.425。

3 各国规范稳定曲线对比

3.1 整体稳定折减系数曲线

为便于钢桥设计的实际应用，在介绍各国规范的整体稳定系数计算方法时，已经将其统一表示为以相对长细比为自变量的函数，如式(21)、式(29)、式(6)、式(15)所示。另外，引入欧拉临界荷载对应的整体稳定系数作为参照，如式(36)所示。

(36)

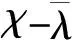
可以看出，所有规范中的曲线均低于欧拉曲线。欧洲规范5条曲线由a0向d折减系数依次递减，中国公路规范4条曲线也由a向d递减，并与欧洲规范中a、b、c、d曲线差别很小。美国和日本规范均只有一条曲线，其中美国规范取值较大，日本规范较小。当相对长细比大于2.5时，所有规范的曲线趋于与欧拉曲线重合。

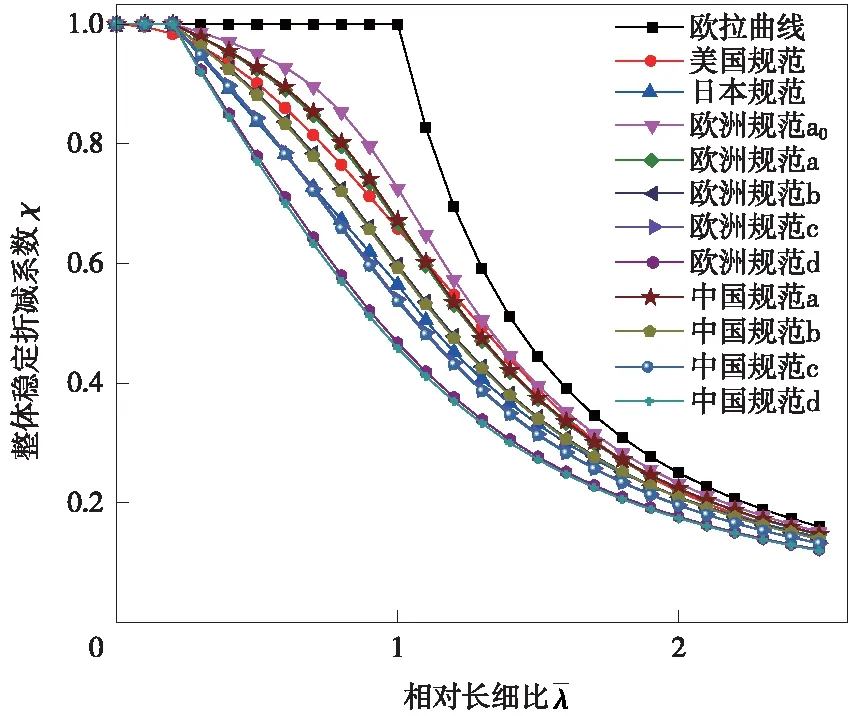
图1 整体稳定折减系数曲线

3.2 局部稳定折减系数曲线

各国规范局部稳定的计算方法差异，可以由局部稳定系数和相对宽厚比的函数曲线来直观对比。此处引入板件弹性屈曲荷载对应的局部稳定系数作为参照，如式(37)所示。

(37)

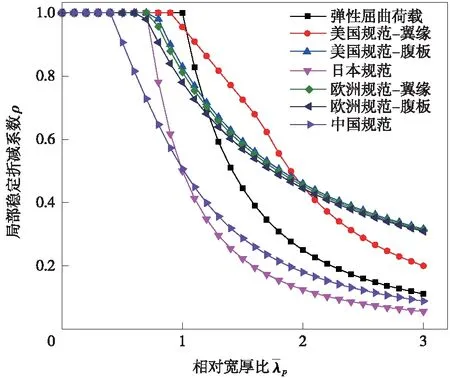
图2 局部稳定折减系数曲线

欧洲和美国规范中腹板和翼缘的局部稳定折减系数曲线均部分或全部高于弹性屈曲荷载曲线，说明这两种规范均利用了板的屈曲后强度。而中国和日本规范取值均低于欧拉屈曲荷载，且日本规范最为安全，在相对宽厚比>3.0后与弹性屈曲荷载曲线趋于重合。

3.3 焊接H形截面稳定曲线

对于钢结构桥梁中的焊接H形截面，其常用的板件厚度通常≤40 mm。当翼缘板的厚度≤40 mm时，欧洲规范和中国规范均取各自规范中的c曲线来计算整体稳定折减系数。为方便对比，单独提取各国规范中计算焊接H形截面所对应的4条整体稳定系数曲线，如图3所示。可以看出，在计算整体稳定系数时，美国规范取值最大，日本规范其次，欧洲规范和中国规范取值最小，且两者非常接近。

图3 H形截面整体稳定折减系数曲线

各国规范的翼缘局部稳定系数曲线较为分散，如图4所示。中国规范最先开始折减，其余规范则在相对宽厚比约为0.8时开始折减。当相对宽厚比>1.2时，美国规范和欧洲规范均已高于弹性屈曲荷载，两条曲线交替上升，当相对宽厚比>2.0时，欧洲规范取值更大；中国公路规范和日本规范一直低于弹性屈曲荷载，当相对宽厚比>1.0时，中国公路规范取值更大。

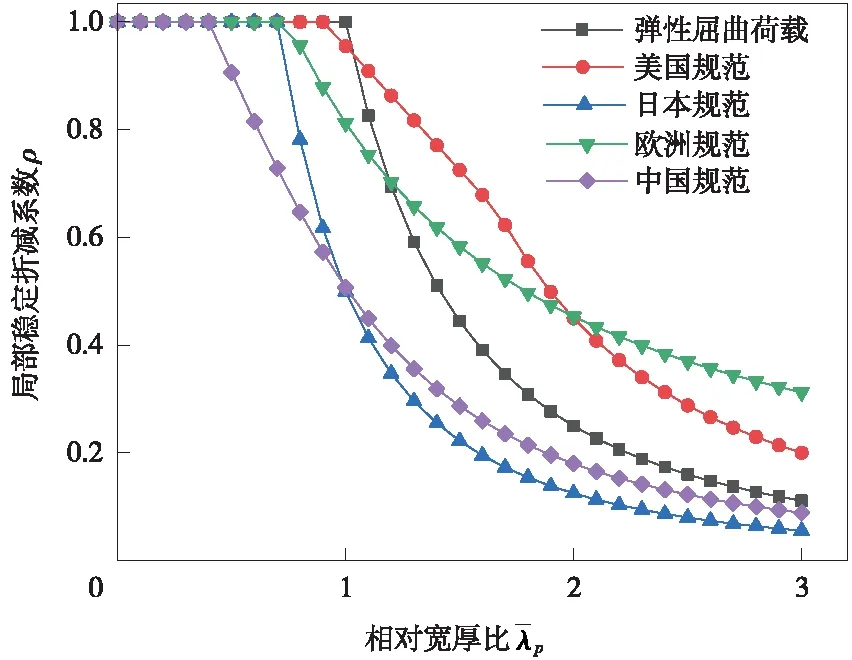
图4 H形截面翼缘局部折减稳定系数曲线

各国规范的腹板局部稳定系数曲线分布规律与翼缘曲线基本相似，如图5所示。不同的是美国规范曲线一直高于欧洲规范曲线，但差值越来越小。

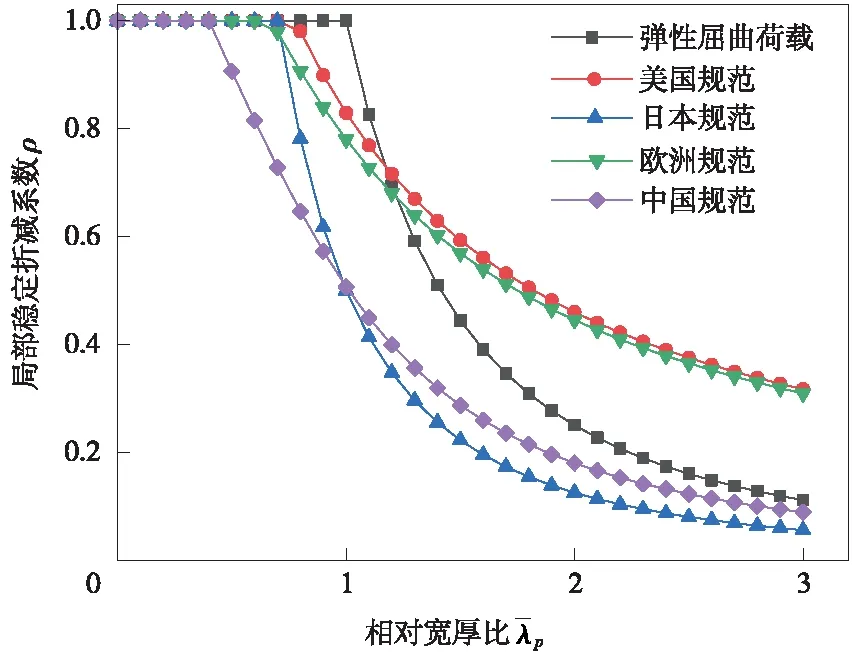
图5 H形截面腹板局部稳定折减系数曲线

4 算例

选用某下承式钢桁梁桥中的2个焊接H形截面进行相关稳定折减系数的计算。钢材种类为Q345qD，截面尺寸如图6所示。截面1杆件为上弦杆，长度8 m；截面2杆件为腹杆，长度13.6 m。

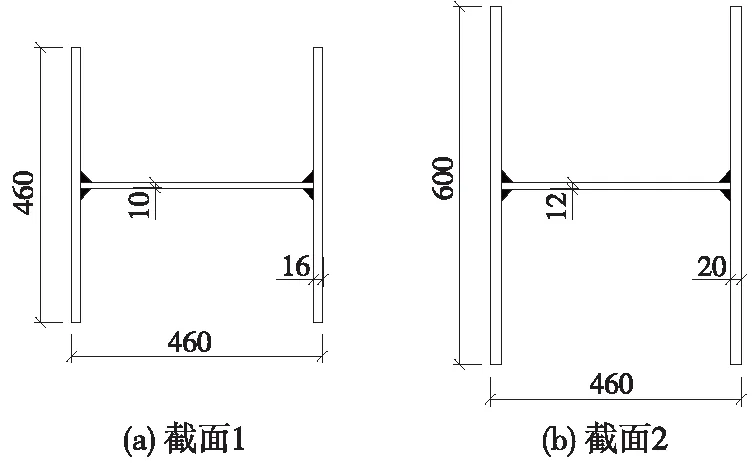
图6 杆件截面尺寸示意(单位：mm)

根据不同规范计算杆件的整体稳定折减系数，以及翼缘和腹板的局部稳定折减系数，计算结果如表3所示。表3中仅列出弱轴平面(腹板平面)的整体稳定折减系数。杆件的计算长度根据各国规范中的相关规定进行取值。

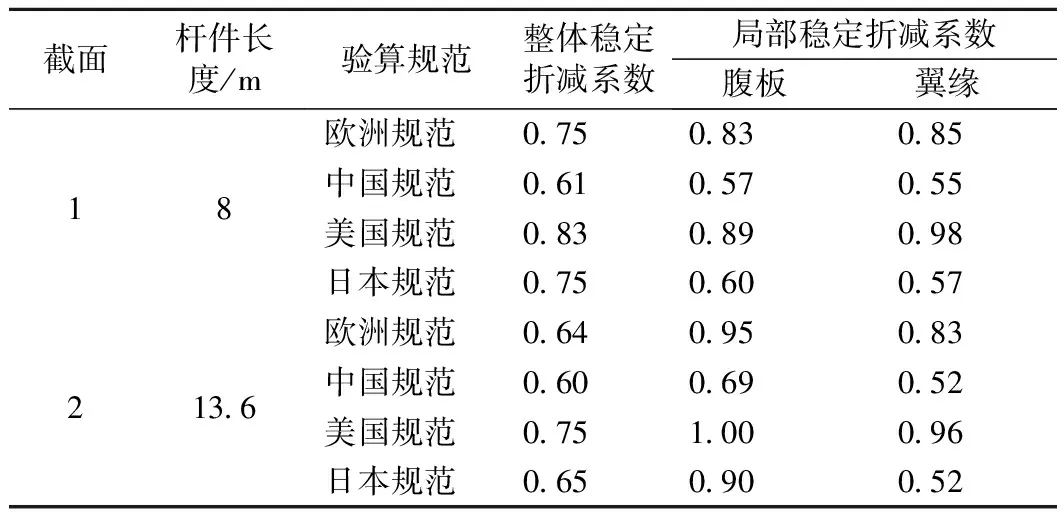
表3 杆件稳定折减系数

由表3可以看出，对于相同的截面，在考虑整体稳定时，美国规范折减系数最大，欧洲规范、日本规范其次，二者非常接近，中国规范最小；进行局部稳定折减时，各国规范差异很大，由于欧洲和美国规范利用了板的屈曲后强度，折减系数明显大于中国规范和日本规范，其中中国规范局部稳定折减系数最小。

5 结论

(1)在考虑整体稳定影响时，欧洲和中国规范以试验曲线结合Perry公式给出计算方法，美国和日本规范则采用经验公式。

(2)考虑局部稳定影响时，美国和日本规范按照经验公式进行计算，欧洲和中国规范则利用了Karman的有效宽度概念，其中欧洲规范采用Winter公式，而中国规范仍采用Perry公式来计算。

(3)欧洲和中国规范的整体折减稳定曲线较为接近，不同截面类型对应不同的屈曲曲线；美国和日本规范只有一条整体稳定折减曲线，其中美国规范曲线偏高，日本规范偏低。

(4)欧洲和美国规范的局部稳定折减曲线偏高，位于弹性屈曲荷载曲线的上方，利用了板的屈曲后强度；日本和中国规范曲线则偏低，低于或者接近弹性屈曲荷载曲线。

(5)根据各国规范结合实例计算稳定折减系数，计算结果差异很大。整体稳定折减系数方面，美国规范最大，欧洲、日本规范其次，二者非常接近，中国规范最小；局部稳定折减系数方面，美国规范最大，欧洲规范其次，日本和中国规范最小，且两者较为接近。中国规范的稳定设计最为保守。