侧阻附加弯矩对桥梁桩基水平承载力影响研究

竺明星,戴国亮,卢红前,龚维明,万志辉

(1.中国能源建设集团江苏省电力设计院有限公司,南京 211102； 2.东南大学土木工程学院,南京 211189)

引言

桩基础由于其构造简单、施工便利、承载力大等优点被广泛应用于高层建筑、桥梁等工程中[1]。桥梁水平受荷桩桩身响应求解的众多方法中，基于Winkler模型的弹性地基梁法是最常用的方法[2]。然而，弹性地基梁法将桩等效为一维杆单元进而无法考虑桩径尺寸效应的影响。事实上，桥梁桩基础的直径普遍较大，随着桩径的增加，基桩水平承载特性的尺寸效应问题越来越显著[3]。

Lam等[4]认为桩身产生水平变形时，桩身前后两侧竖向摩阻力将形成力偶作用且随着桩径、桩身截面转角的增加而增加，并首次提出附加弯矩-转角概念。McVay等[5]开展了竖向侧摩阻力对嵌岩桩水平承载特性影响的离心模型试验研究，结果表明嵌岩桩较高的竖向侧摩阻力所产生的附加弯矩效应非常显著，不能忽略。上述研究尚未求得考虑附加弯矩影响的桩身响应解。霍少磊[6]假定桩侧摩阻力为定值，进而求解了考虑侧阻附加弯矩影响的水平受荷桩桩身响应解，但由于假设的局限性使得结果应用受到限制且只考虑单一的侧阻附加弯矩影响因素。Alikhanlou[7]、Tseng[8]采用能量法开展沉井侧壁竖向摩阻力、端部水平阻力对超大直径沉井水平承载特性的理论研究，结果表明考虑竖向侧摩阻力影响时沉井在泥面处的变形比不考虑的情况小40%左右，且结果与实测值更为接近，同时，这一影响随着基础直径的增加而增加。Gerolymos等[9]综合考虑沉井侧附加弯矩、沉井端部水平阻力及端部土抗力产生的反弯矩等影响因素，建立四弹簧Winkler弹性地基梁模型，并解得沉井水平响应弹性解。然而这些求解理论均假定地基土体为弹性模型，当水平荷载较大时，这些理论计算所得结果将明显偏小。Varun等[10]通过大量有限元分析发现：当基础长径比较大时，基础底部竖向土抗力产生的反弯矩作用可忽略不计，王伯惠[11]也得出相同的结论，因此Ashour等[12]认为桩基础只考虑桩侧水平土抗力、桩侧竖向摩阻力产生的附加弯矩以及桩端底部水平阻力即可满足工程精度要求。

本文首先推导了任意桩侧摩阻力τ-s曲线作用下的桩侧摩阻力附加弯矩计算表达式；随后推导得出桩端水平阻力解析表达式。基于传递矩阵法原理[13]并结合桩土相互作用p-y曲线模型，分别求得了桩身弹性段、塑性段传递矩阵系数解析解，进而得出考虑侧阻附加弯矩效应的桥梁基桩水平承载力半解析解。通过案例对比验证了本文方法和推导的正确性。最后开展了附加弯矩对桥梁基桩水平承载特性影响的参数分析。

1 桩身响应模型建立与求解

1.1 解析模型建立

如图1所示，圆形截面桩的总长为L，桩垂直嵌入成层地基土中。为后文表述便利，按照张玲等[14-15]作法，将地面上自由段桩侧引入“虚拟土层”，因此总土层数(包含虚拟土层)为n层，第i层土中对应的桩长、桩径以及抗弯刚度分别为Hi、di和EIi。桩顶分别作用水平荷载Ft、弯矩荷载Mt。地面上桩身作用分布力q(z)。

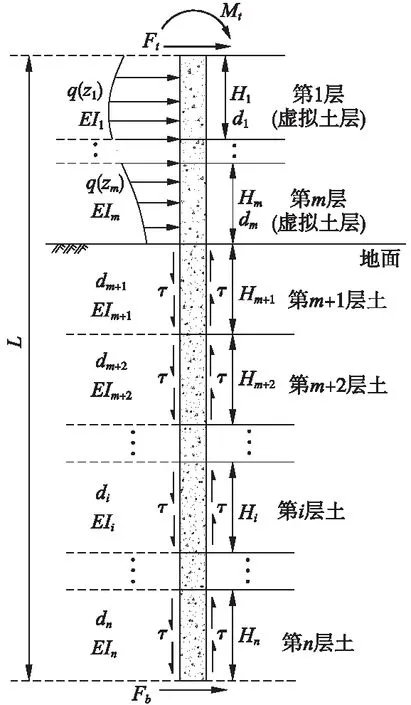
图1 桩身解析模型

推导过程中假定图1所示的模型符合Winkler弹性地基梁模型的假设条件，同时各物理量正负号规定与文献[14，16]规定一致。

1.2 桩侧竖向摩阻力产生的附加弯矩

为推导地面下任意桩身截面的侧阻附加弯矩作用，将桩身截面按照转角正值的规定逆时针旋转任意θ角度，如图2(a)所示；相应的桩身竖向侧摩阻力沿桩周的分布如图2(b)所示。此时，桩侧竖向摩阻力作用产生的侧阻附加弯矩以顺时针旋转为正，如图2所示。

由图2(b)可知，当桩身截面产生转角变形时，桩侧竖向侧摩阻力沿桩周呈非线性分布特征，且桩周摩阻力分布状态受截面转角以及假定的桩侧摩阻力τ-s曲线模型的影响非常显著，很难得出侧阻附加弯矩一般性解析解。

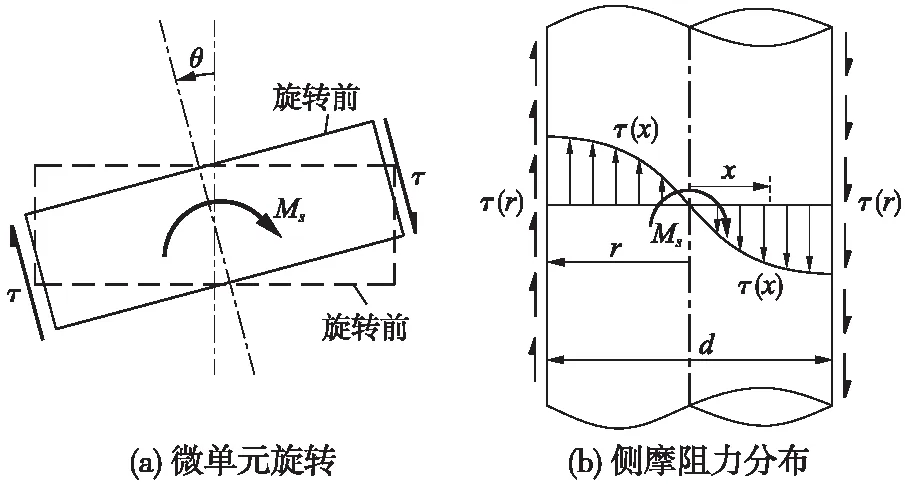
图2 桩身竖向侧摩阻力分布示意

本文采用McVay等[5]离散叠加求和的思路推导竖向侧摩阻力产生的附加弯矩计算表达式。如图3所示，取地面下任意深度处桩身截面的剖面。

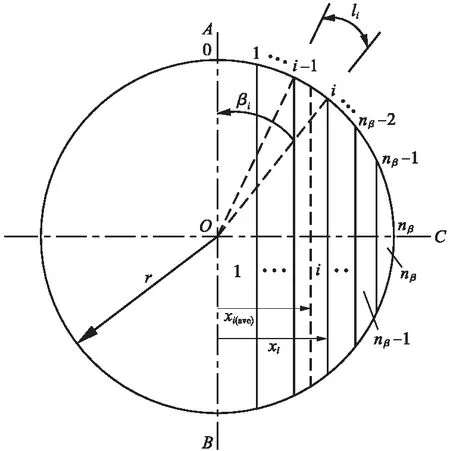
图3 桩身横截面离散示意

(1)

式中，βi=i×π/(2nβ)，为等分后任意角度；li=πr/(2nβ)，为等分之后每小段圆弧的弧长度；r为桩身半径。

Msi=τi(ave)lixi(ave)

(2)

将公式(1)代入公式(2)并求和可得任意截面处竖向侧摩阻力产生的附加弯矩

(3)

式中，Ms为只考虑桩侧土压力被动区竖向摩阻力所产生的附加弯矩作用，kN·m/m，顺时针旋转为正，其物理含义为桩身单位长度上作用的抗力矩[5，9]。

1.3 桩端水平阻力模型

针对大直径基础，Gerolymos等[9]综合考虑水平土抗力、侧阻附加弯矩、沉井端部水平阻力及端部土抗力产生的反弯矩等影响因素，提出如图4所示的受力模型体系。然而，Varun等[10]通过大量有限元分析发现：当基础长径比大于1时，基础底部土体竖向应力(σz)产生的反弯矩Mb可忽略不计。王伯惠[11]、Ashour等[12]也认为对于桩基础而言，基础底部反弯矩Mb作用可以忽略。因此，只考虑桩端水平阻力Fb的作用。

Ashour等[12]提出地基土体为黏性土时的桩端水平阻力-桩端位移(Fb-yb)本构关系为

(4)

式中，Fb为桩端水平阻力，kN；Cu为黏性土不排水抗剪强度，kPa；Ab为桩端横截面积；yb为桩端水平位移；d为桩径；ε50为三轴仪实验中最大主应力差一半时对应应变值；v为泊松比。

然而公式(4)是针对黏性土提出，对于非黏性土无法直接使用。因此，对公式(4)进行求导得出桩端水平阻力-位移模型的初始刚度

(5)

式中，kby为桩端水平阻力-桩端位移(Fb-yb)关系曲线的初始刚度，kN/m。

由于E50(=Cu/ε50)为对应50%强度的割线模量，同时土体E50模量与弹性模量E之间的关系[17]如下

(6)

式中，Rf为破坏比，Plaxis推荐该值取为0.9。

将公式(6)代入公式(5)化简后可得

(7)

公式(7)即为推导所得的桩端水平阻力-桩端位移(Fb-yb)关系曲线初始刚度计算表达式，该公式只与土体的弹性模量E、泊松比v以及桩径d相关，适用于任意性质的土体。

当桩端水平位移yb达到一定值时，桩端水平阻力将达到极限值Fbu，随着水平位移yb的增加，Fbu保持不变，则桩端极限阻力为

Fbu=τbuAb=πτbud2/4

(8)

式中，τbu为桩端与土体极限侧摩阻力，当桩端土体为黏性土时，τbu为不排水抗剪强度Cu；当端部土体为砂土或c-φ土时，τbu=c+σvtanδ，c为土体的黏聚力，其中砂土c=0；σv为桩端位置处上覆土体自重产生的有效竖向应力；δ为桩端与土体之间的界面摩擦角，一般取为0.75φ[18]，φ为桩端土体内摩擦角。

桩端水平阻力-位移一般呈非线性特征[12]，因此结合公式(7)和公式(8)，建立双曲线型桩端水平阻力-桩端位移(Fb-yb)本构关系式

(9)

1.4 虚拟土层中桩身传递矩阵系数

如图1所示，地面上自由段桩侧不存在地基土体，此时“土体”假定为虚拟土层；同时，如果地面下某一层的地基土非常软弱时，设计过程中忽略该层土体水平抗力作用，亦可采用虚拟土层的假定。

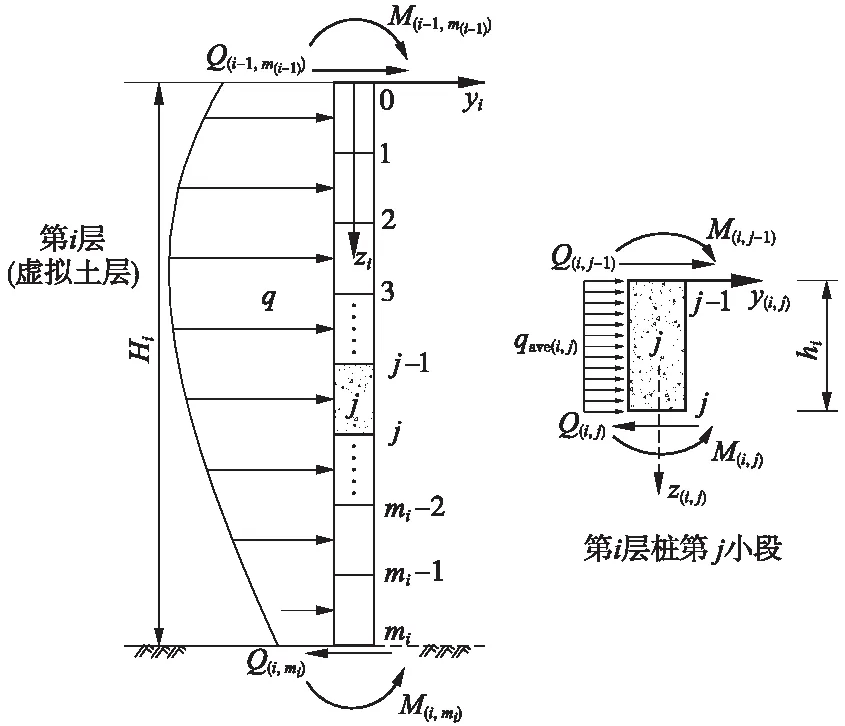
图5 虚拟土层中桩身离散示意

任取第i层虚拟土层，如图5所示，该层土中的桩被等分为mi份，则第i层中桩等分后的每小段桩长度为hi=Hi/mi。根据传递矩阵法原理并结合文献[13，15]可得第i层虚拟土层中第j小段桩身传递方程为

S(i，j)=U(i，j)S(i，j-1)

(10)

式中，S(i，j-1)=[y(i，j-1)θ(i，j-1)M(i，j-1)Q(i，j-1)1]T以及S(i，j)=[y(i，j)θ(i，j)M(i，j)Q(i，j)1]T分别为第i层虚拟土层中第j小段桩的桩顶与桩端变形、转角、弯矩和剪力状态矩阵向量；U(i，j)为第i层中第j小段桩的桩身传递矩阵系数，根据Laplace正逆变换可得

(11)

式中，qave(i，j)为第i层中第j小段桩的桩侧平均分布荷载，等于(q(i，j-1)+q(i，j))/2；q(i，j-1)和q(i，j)分别为第i层中第j小段桩的顶部与底部位置处分布荷载值。

1.5 地面下弹性阶段桩身传递矩阵系数

1.5.1 桩身微单元受力模型

取地面下桩身微单元并假定该段的桩土作用处于弹性阶段，如图6所示。由桩身微单元弯矩平衡可得

(12)

式中，Ms，ave为单侧竖向摩阻力产生的弹性段范围内桩身附加弯矩平均值，kN·m/m。

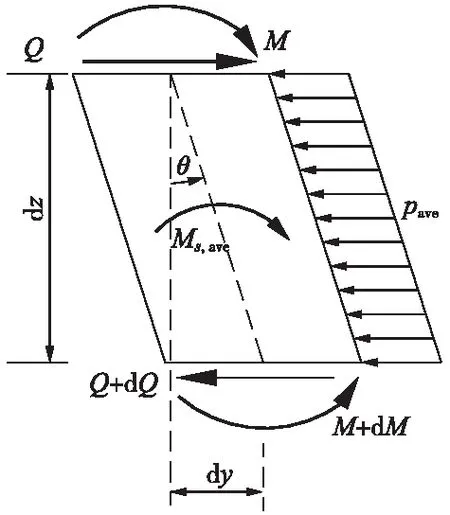
图6 弹性段桩微单元受力分析

1.5.2 弹性段桩身传递矩阵系数

如图7所示，假定地面下第i层桩被离散等分为mi份，离散等分后每小段桩长度为hi=Hi/mi。取等分后的第j小段分析，采用Laplace正逆变换，建立如下微分方程组

(13)

式中，y(i，j)、θ(i，j)、M(i，j)和Q(i，j)分别为第i层桩中第j小段桩端水平位移、转角、弯矩和剪力；kave(i，j)为第i层桩中第j小段桩的桩侧土抗力模量平均值，等于(k(i，j-1)+k(i，j))/2，其中k(i，j-1)和k(i，j)分别为第i层桩中第j小段桩的顶部与底部位置处土抗力模量；Ms，ave(i，j)为第i层桩中第j小段桩的桩身附加弯矩平均值，等于(Ms(i，j-1)+Ms(i，j))/2，其中Ms(i，j-1)和Ms(i，j)分别为第i层桩中第j小段桩的顶部与底部位置处竖向侧摩阻力引起的附加弯矩值。

采用公式(3)计算Ms(i，j-1)和Ms(i，j)过程中，侧摩阻力τ所需的转角θ值采用前一次迭代计算所得的转角值，首次迭代计算时假定任意截面处的Ms(i，j)均为0。

令β(i，j)=[kave/(4EIi)]0.25，结合文献[13，15]可解得方程组(13)为

S(i，j)=U(i，j)S(i，j-1)

(14)

式中，S(i，j-1)=[y(i，j-1)θ(i，j-1)M(i，j-1)Q(i，j-1)1]T以及S(i，j)=[y(i，j)θ(i，j)M(i，j)Q(i，j)1]T分别为地面下土层中第i层中第j小段桩的桩顶与桩端变形、转角、弯矩和剪力状态矩阵向量；U(i，j)为第i层中第j小段桩(处于弹性阶段)的桩身传递矩阵系数，如下所示

U(i，j)=

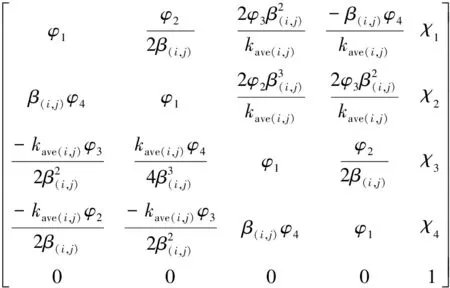
(15)

其中χ1、χ2、χ3和χ4分别为

(16)

上述两式中：令t(i，j)=β(i，j)hi，则φ1、φ2、φ3和φ4为

(17)

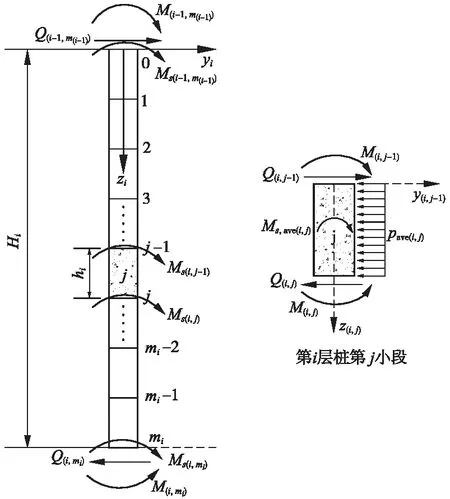
图7 弹性段桩身离散示意

1.6 地面下塑性阶段桩身传递矩阵系数

如图7所示，假定地面下第i层桩土相互作用为塑性阶段，该段桩被离散等分为mi份，离散等分后每小段桩长度为hi=Hi/mi。取等分后的第j小段分析，此时图7中的桩侧土抗力平均值pave(i，j)替换为极限土抗力平均值pu，ave(i，j)，则采用下式计算

pu，ave(i，j)=(pu(i，j-1)+pu(i，j))/2

(18)

式中，pu(i，j-1)和pu(i，j)分别为第i层桩中第j小段桩的顶部与底部位置处极限土抗力值。

将公式(13)中kave(i，j)y(i，j)采用公式(18)替换并结合Laplace正逆变换可解得第i层中第j小段桩(处于塑性阶段)的桩身传递矩阵系数

U(i，j)=

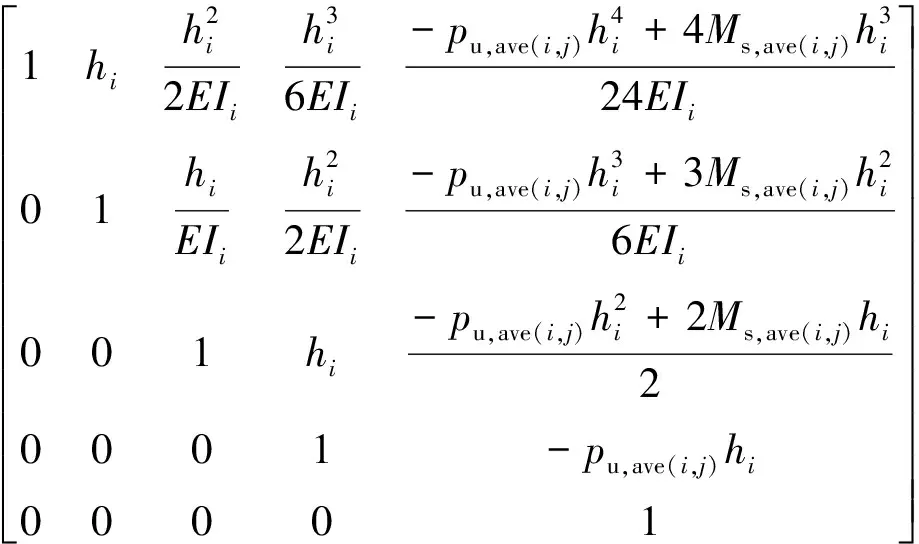
(19)

1.7 桩身响应求解

根据传递矩阵法原理[13，15]可得整个桩身的传递矩阵方程为

Sn=U(n，mn)…U(i，j)U(i，j-1)…U(1，1)S0

(20)

其中，Sn=[ynθnMnQn1]T和S0=[y0θ0M0Q01]T分别为整个桩的桩端和桩顶处变形、转角、弯矩和剪力的状态矩阵向量；U(i，j)为桩身传递矩阵系数，当桩侧土体为虚拟土体时采用公式(11)计算，当桩侧土体为弹性阶段时采用公式(15)计算，当桩侧土体处于塑性阶段时采用公式(19)计算。

为求得桩顶响应矩阵S0，需引入桩顶、桩端边界条件。常见的边界约束条件主要有自由、铰接和嵌固，如下所示

(21)

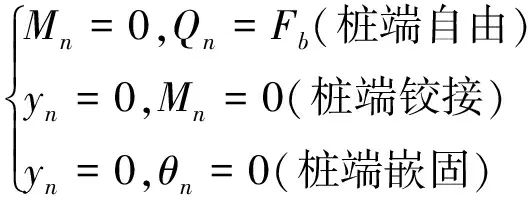
(22)

公式(22)中，桩端自由边界条件时桩端水平阻力Fb采用公式(9)计算，其中第1次迭代计算时假定Fb值为0，随后采用前一次迭代计算所得桩端位移yb计算Fb值。

根据桩顶、桩端边界条件将公式(21)、公式(22)中对应值代入公式(20)中即可解得桩顶响应矩阵S0，则任意位置处的桩身响应为

S(i，j)=U(i，j)U(i，j-1)…U(1，1)S0

(23)

由于桩身响应求解过程中可能选取非线性或弹塑性桩土相互作用p-y曲线模型以及侧阻附加弯矩Ms需要迭代才能求解，则本文方法桩身响应求解迭代详细步骤如下。

(1)第1次计算时假定桩土相互作用均处于弹性阶段，桩侧土抗力模量取p-y曲线的线性段土抗力模量或取p-y曲线模型初始土抗力模型；由于侧阻抗力矩依赖于桩身截面转角，初始计算时可假定转角均为0，此时位置处Ms，ave(i，j)的值均为0；当桩端自由边界条件时假定Fb值为0。

(2)根据前一次计算结果，将桩身截面转角带入公式(3)重新计算附加弯矩Ms，ave(i，j)；如果桩土相互作用处于弹性阶段时，则按照割线刚度法重新计算任意截面处土抗力模量值；当桩土相互作用处于塑性阶段时，土抗力采用p-y曲线模型极限值计算；当桩端为自由边界条件时，根据前一次计算所得桩端位移yb重新计算Fb值；重新计算考虑附加弯矩作用的弹性段和塑性段桩身传递矩阵系数，并结合新的边界条件值进而重新解得桩身响应。

(3)经过s次迭代后，判断任意截面处桩身转角是否满足下述精度要求

(24)

如果不满足公式(24)所述的精度要求，则按照第(2)步重新计算；如果满足精度要求，则按照公式(23)输出任意截面处桩身响应值。

2 案例验证

Bhushan等[20]在硬质黏性土中开展了灌注桩水平承载特性试验研究。总桩长L=5.185 m，地面上长度为0.23 m，地面下长度为4.995 m，桩径d=1.22 m，抗弯刚度EI=2.25×106kN·m2。桩长范围内土体为均质硬黏土，根据文献[21]可得该土体弹性模量为24.44 MPa，泊松比v=0.3，则根据公式(5)可知kby=1 039 kN/m。桩土相互作用p-y曲线采用API规范推荐的黏土模型，不排水剪切强度Cu=227 kPa；有效重度γ=18.8 kN/m3；ε50=0.007 2。

桩侧竖向摩阻力曲线采用API规范推荐模型，如表1所示。API规范附录中规定：“当黏性土不排水剪切强度Cu>72 kPa时，τu=0.5Cu”，因此τu=113.5 kPa；su为相对位移极限值，Mokwa[22]等认为桩侧摩阻力完全发挥所需的桩土相对位移为2.54～7.62 mm，其中较小的值对应于打入桩，较大的值对应于灌注桩；而Juirnarongrit等[23]认为极限位移值su与桩长、桩径无关，一般在5～8 mm之间。从偏于安全的角度出发本文取su=8 mm。

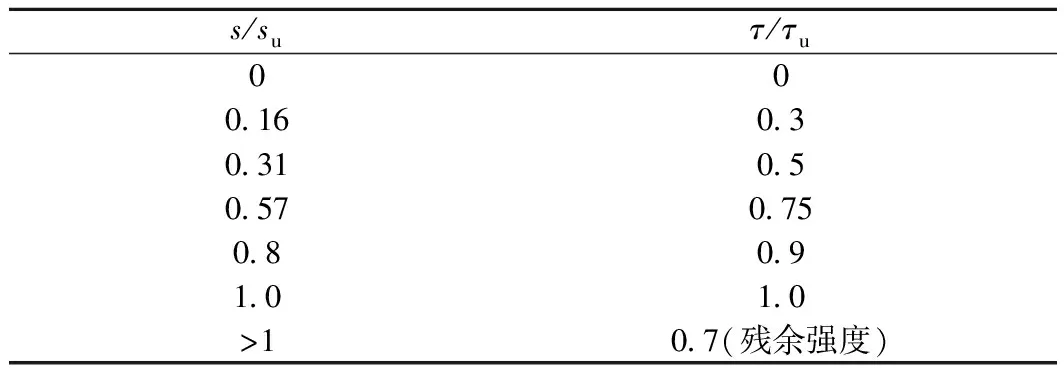
表1 归一化侧摩阻力曲线

根据公式(8)得出桩端水平阻力极限值Fbu=265.36 kN，按公式(9)可得Fb-yb关系为

(25)

则根据本文方法可得桩顶变形计算结果与实测对比如图8所示。

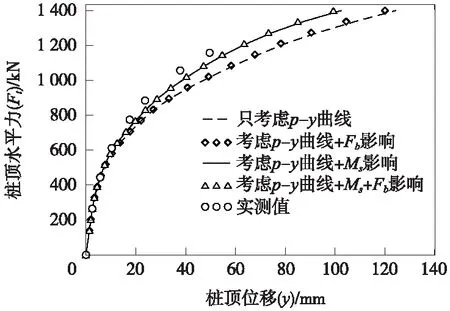
图8 不同工况条件下桩顶荷载-位移对比

根据图8可知：当只考虑桩土相互作用p-y曲线时的计算结果与实测值相差较大，且差异随着荷载的增加而显著增加(最大误差约40%)；如图8中“考虑p-y曲线+Ms影响”所示，本文考虑侧阻附加弯矩影响时的计算结果与实测值非常接近，最大误差不超过9%，这是由于地基土体为硬质黏性土，相应的桩侧摩阻力较大(τu=113.5 kPa)，此时桩身竖向摩阻力产生的附加弯矩Ms对水平承载特性影响显著，已不能忽略。从图中还可明显看出：考虑桩端水平阻力Fb作用时的计算结果与相同工况下不考虑Fb作用的结果几乎完全一致，即桩端水平阻力Fb作用可忽略不计，这是由于随着桩顶荷载增加，桩端阻力Fb值尽管也增加，但其量值太小，对整体受力可忽略不计，如图9所示。

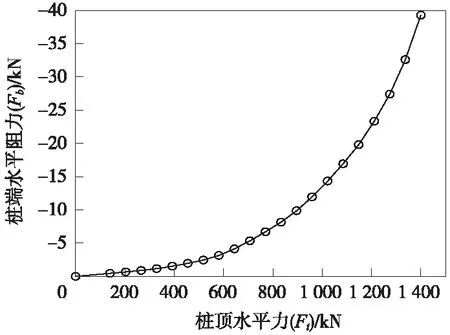
图9 桩端水平阻力

3 附加弯矩参数影响分析

为研究附加弯矩对水平受荷桩承载力的影响，以“案例验证”的模型为背景，分别开展不同桩侧摩阻力τ-s曲线、桩长径比等因素影响分析。

3.1 桩侧摩阻力τ-s曲线的影响

关于黏性土层中灌注桩极限摩阻力发挥时对应的极限位移值su，不同学者得出不同值：Mokwa[22]认为su为2.54～7.62 mm，Juirnarongrit等[23]取为5～8 mm，美国桥梁标准[24]取为6.1 mm(=0.005d，d为桩径)，而肖宏彬[24]通过统计得su为2～20 mm。因此本节分析时su最小值取为2 mm，最大值为20 mm；极限摩阻力τu分别取56.75，113.5 kPa和227 kPa；残余强度比值分别取0.7和1.0，进而建立如表2及图10所示的模拟工况。

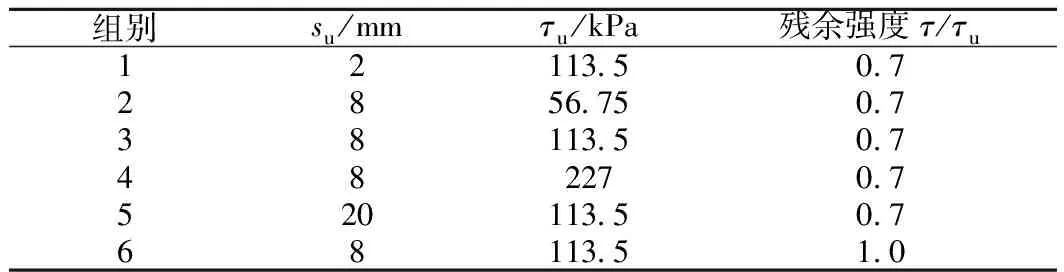
表2 侧摩阻力曲线计算工况

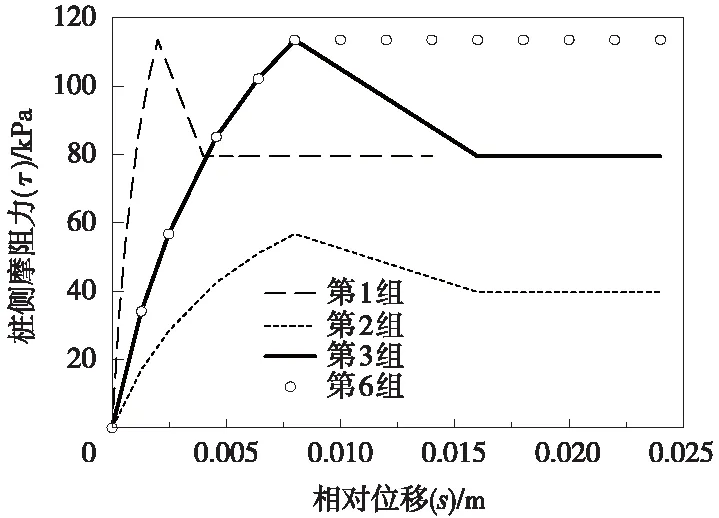
图10 不同侧摩阻力曲线模型

图11为只考虑p-y曲线作用时桩顶荷载-位移关系，从图11可看出，桩身失稳时的极限加载值Fc≈2 000 kN，而桩身水平极限承载力Fu≈1 640 kN。

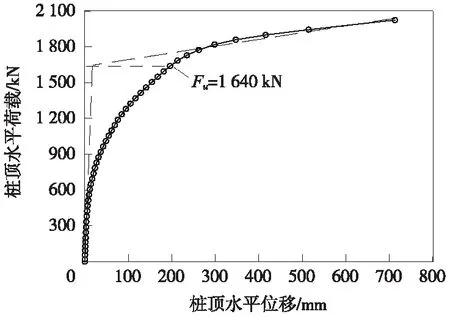
图11 桩顶荷载-位移曲线

图12为6种工况情况下桩身最大位移降低幅度(与不考虑附加弯矩效应时结果对比)关系。由图12可知，桩顶水平荷载作用下变化规律基本一致且主要分为4个阶段：

第①阶段，加载初始阶段(Ft=0～0.15Fu)的桩身最大位移降低幅度几乎保持不变。这是由于桩身变形和转角非常小，桩侧摩阻力发挥基本保持在线弹性阶段导致的。

第②阶段，随着桩顶水平荷载Ft的持续增加，最大位移降低幅度增加至最大值。这是因为桩身转角逐渐增加使得桩侧摩阻力产生的附加弯矩也增加，当相对位移达到极限位移值su时，相应的附加弯矩也将达到最大值。

第③阶段，最大变形降低幅度从最大值开始逐渐降低。这是由于当桩顶荷载Ft逐渐接近桩身极限承载力Fu时，桩身侧摩阻力基本均达到峰值τu，此时侧阻附加弯矩增加量非常微弱，由于桩身变形和转角进一步逐渐增加，进而使得最大变形降低幅度衰减。

第④阶段，当水平荷载超过桩身极限承载力Fu时，很小的荷载增量也会导致很大的位移增量，由此可知，侧阻附加弯矩增量会显著降低桩身水平变形，进而使得最大位移增加幅度显著提高。

如图12(a)可知，极限位移值su越小，最大位移降低幅度最大值越大且对应的桩顶水平荷载值越小。由图12(b)可知，极限侧摩阻力τu越大，相应的最大位移降低幅度整体增加。对比第3组和第6组可知：在相对位移s未达到极限位移值su之前，两组工况结果完全一致；当超过极限位移值su之后，由于第6组的τ-s曲线无衰减和残余阶段，进而使得最大位移降低幅度大于第3组工况。

由图11可知，当水平荷载Ft超过桩身极限承载力Fu时，很小的荷载增量也会导致很大的位移增量，而图12中第④阶段的最大位移降低幅度也完全吻合该特征，因此也可将图12中离极限加载值Fc最近的一个位移降低幅度极小值点所对应的水平荷载定义为桩身极限承载力Fu，从图12可明显看出，该极小值点对应的荷载与通过图11确定的桩身极限承载力Fu几乎一致。

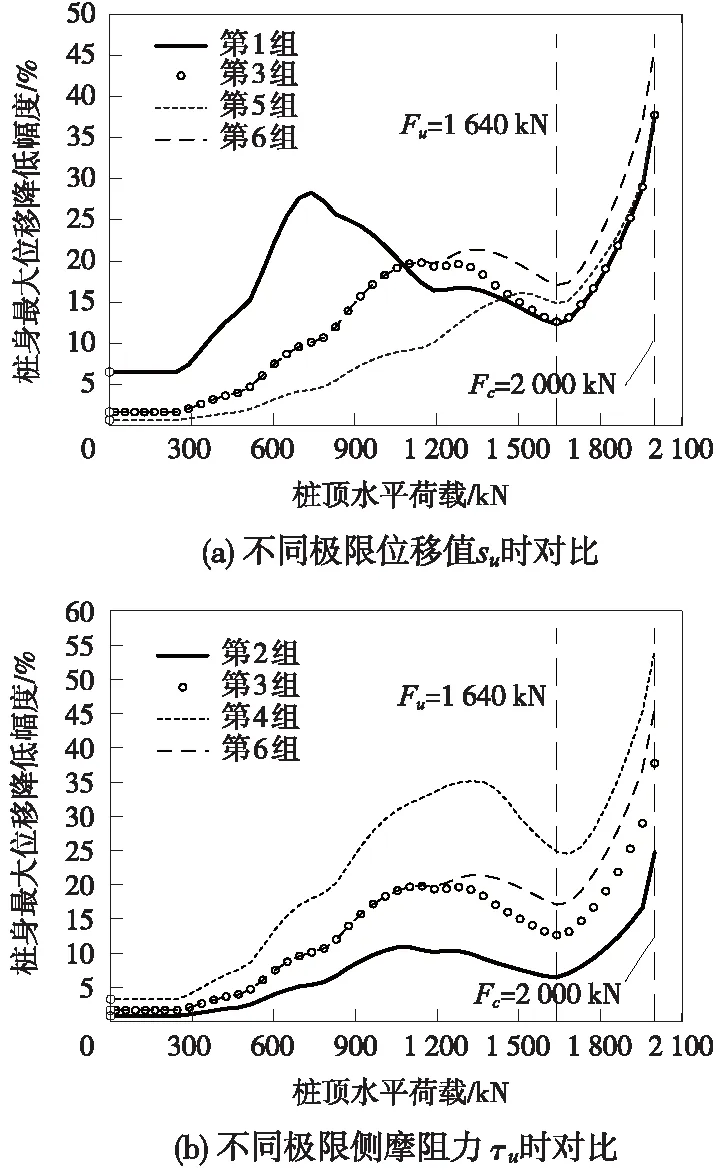
图12 不同τ-s曲线对最大位移影响

3.2 桩长径比影响分析

为研究不同长径比情况下侧阻附加弯矩效应对桩基水平承载特性的影响，假定桩侧摩阻力τ-s曲线采用表2中第2组模型，且忽略柔性桩桩身塑性铰弯矩影响。桩径d=2 m和桩嵌入深度Lb=4 m保持不变，两组桩长径比(Lb/d)均分别为1，2，4，6，8和10。由于桩顶水平荷载Ft具有工程意义的是0～Fu(桩身极限承载力)阶段，因此，图13中横坐标采用Ft/Fu表示。桩长径比(Lb/d)分别为1，2，4，6，8和10时桩身最大变形降低幅度对比如图13所示。

从图13(a)可知，当长径比为1和2时，考虑桩端水平阻力Fb作用时影响较为显著，尤其是Ft/Fu=0.45～1范围内；然而，随着长径比的增加，水平端阻Fb影响明显降低，当长径比等于4时，平均误差小于1%，因此当长径比Lb/d≥4时可忽略水平端阻Fb影响。

由图13可知：考虑侧阻附加弯矩效应时的桩身最大位移降低幅度均随着长径比的增加而逐渐降低，且降低幅度越来越大，当长径比Lb/d=10时，最大位移降低幅度平均值分别为1.8%和0.72%。由此可知,，对于柔性长桩而言，桩侧竖向摩阻力产生的附加弯矩效应对基桩水平承载特性的影响可忽略不计。需要注意的是：长径比Lb/d相同时，桩径d越大，相应的初始阶段最大位移降低幅度也越大。

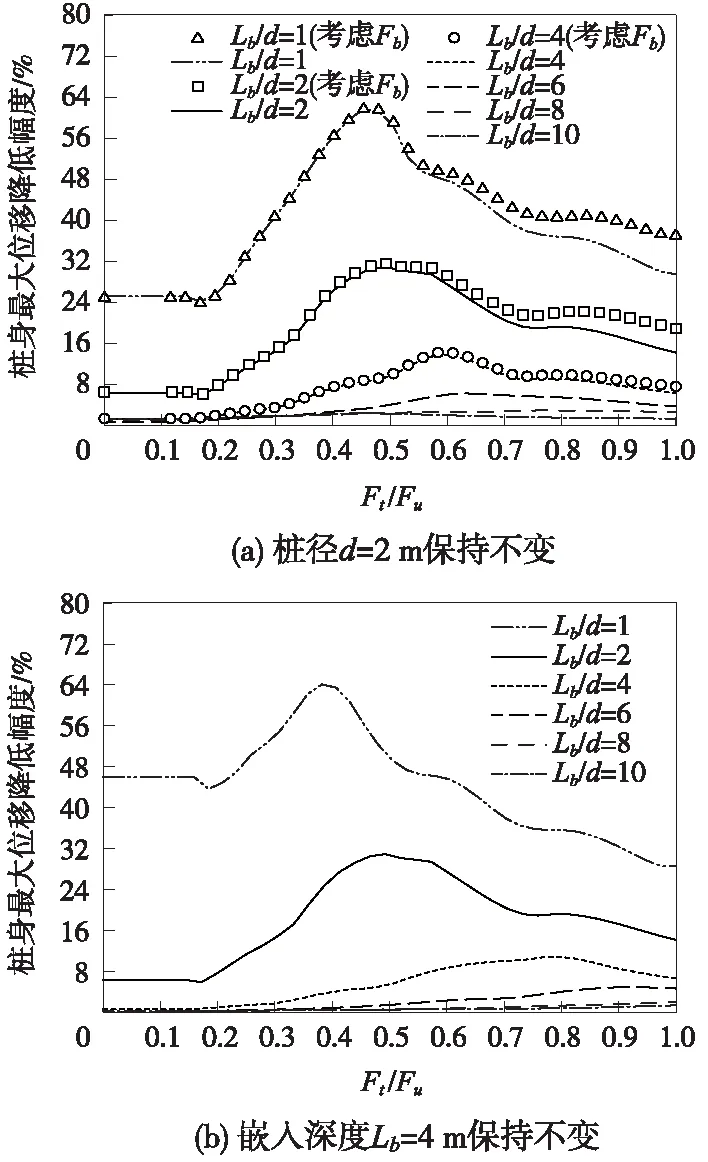
图13 长径比对最大位移影响

4 结论

为分析桩侧竖向摩阻力对桥梁基桩水平承载特性影响，首先引入附加弯矩概念并建立任意桩侧摩阻力τ-s曲线作用时附加弯矩计算公式；随后建立桩端水平阻力双曲线本构模型，在此基础上推导得出桩身传递矩阵系数解析解，并结合给出的迭代求解策略进而解得桩身响应。通过案例对比分析验证了本文方法和解的正确性与合理性。最后，开展了考虑附加弯矩影响的参数分析，得出以下结论。

(1)不同τ-s曲线作用下附加弯矩效应对桩身最大位移降低幅度变化规律均一致，存在4个阶段，即：在Ft=0～0.15Fu时为初始阶段，最大位移降低幅度基本保持常数不变；随着桩顶水平荷载增加，最大位移降低幅度逐渐增加至最大值；随后最大位移降低幅度逐渐减小，当Ft=Fu时达到较小值；最后当Ft=Fu～Fc时最大位移降低幅度快速增加。

(2)极限位移值su越小，最大位移降低幅度最大值越大且对应桩顶水平荷载值越小；极限侧摩阻力τu越大，相应的最大位移降低幅度整体增加。

(3)考虑侧阻附加弯矩效应时的桩身最大位移降低幅度随着长径比的增加而逐渐降低，且降低幅度越来越大，当长径比Lb/d≥10时，可忽略侧阻附加弯矩效应的影响；同时，当长径比Lb/d≥4时可忽略水平端阻Fb影响。

(4)长径比Lb/d相同时，桩径d越大，相应的初始阶段最大位移降低幅度也越大。