系统频率偏差对同时全极化测量的影响及其校准*

刘巧玲，李 超，庞 晨，李永祯，王雪松

(国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室， 湖南 长沙 410073)

雷达目标极化散射特性是目标的固有属性，充分利用该信息可有力提升雷达目标检测、目标分类识别、杂波抑制和抗干扰等能力，对防空反导、侦察遥感、反恐维稳等领域具有重要意义。随着雷达极化技术应用日益深化，极化信息测量的精度已经成为制约雷达应用需求的关键因素之一[1]。例如，在气象观测领域，要实现准确的降水目标分类识别和降雨量预测，要求反射率的测量误差小于1 dB，差分反射率的测量误差小于0.1 dB[2-3]；在地理遥感领域，要保证目标极化分解的精度，要求极化散射矩阵测量的最大归一化均方根误差小于-20 dB[4]。

目前，获取目标全极化信息的方法主要有两种：分时全极化测量和同时全极化测量。分时全极化测量需要两个以上脉冲才能得到目标的极化散射矩阵(Polarization Scattering Matrix, PSM)，对于高速运动目标，该方法存在严重的极化去相关效应[5]。同时全极化测量仅需单个脉冲就可以得到目标的极化散射矩阵，对导弹等高速大机动运动目标具有天然优势。20世纪90年代，同时全极化测量体制雷达得到发展，研究表明：雷达天线和通道特性、发射波形、雷达所处的环境、电磁波传输路径、信号处理算法、目标运动等因素都会影响极化测量的精度[6]。雷达系统中天线对极化测量的影响最为突出，Chandrasekar等[7]首次分析了天线方向图对气象雷达极化测量的影响，其后Zrnic、Galletti等[8-9]提出了两种主极化和交叉极化方向图模型，并基于此模型分别分析了天线交叉极化方向图对不同气象雷达极化测量参数的影响。为了修正雷达天线串扰和通道幅相不一致等对极化测量的影响，20世纪80年代初开始，大量学者对极化校准方法进行了研究。Sarabandi等[10]提出的隔离天线校准技术(Isolation Antenna Calibration Technology, IACT)，Whitt等[11]提出的广义校准技术(General polarimetric radar Calibration Technique, GCT)、Chen等[12]提出的三目标校准技术(Three-Targets Calibration Technique, TTCT)、Fabregas等[13]提出的目标旋量校准算法(Target Spinor Calibration, TSC)基于不同的测量误差模型，对雷达通道和天线等非理想因素进行了分析和校准。上述工作将雷达天线和通道对极化测量的影响建模为乘性误差矩阵，较好地解决了分时全极化测量体制下雷达天线和通道对极化测量的影响。同时全极化测量对波形和信号处理方法提出了更高要求，Giuli等[14]于1993年首次提出用于同时极化测量的正交波形；其后，国内外多位学者针对同时全极化信号波形及其信号处理方法开展了大量研究，设计了基于Golay序列[15]和复合编码[16]的同时全极化测量波形，并基于不同的同时全极化波形设计了信号处理方法[17-19]，对波形非正交性[20-22]和目标运动[23]也提出了一些抑制和补偿方法。

事实上，雷达系统的非理想因素不仅仅包含天线和通道的非理想特性，频率的稳定度、模拟器件的非理想性、信号传输路径等因素均会对同时全极化结果产生影响。在无线通信系统中，正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)系统对同步偏差非常敏感，由于其收发两端晶振的不完全匹配，造成收发两端存在采样频率偏差，从而影响OFDM系统子载波间的正交性。文献[24-26]详细论述了OFDM系统中采样频率偏差带来的影响。类似地，同时全极化测量过程中，经模数转换(Analog Digital Converter, ADC)之后的数字回波信号与本地信号相关(或混频)，由于采样频率偏差的存在，两路数字信号之间存在与采样频偏线性相关的时间失配项，该失配项经过信号处理之后会对极化测量结果调制一个与调频斜率相关的相位项。由于同时全极化测量体制雷达通常采用斜率相反的线性调频(Linear Frequency Modulation, LFM)信号，因此会在不同的极化通道之间引入两个极性相反的相位项。同时，由于上述时间失配误差不能作为乘性误差或者加性误差直接归类到现有极化测量误差模型中，因此，需要对此类误差的产生及影响进行分析，并在理论分析的基础上，提出可行的校准方法。

1 全极化雷达数字去斜原理

1.1 信号模型

基于数字去斜的同时全极化雷达测量流程如图1所示，图中虚线部分表示数字去斜处理过程。首先对两路极化接收信号下变频，经ADC得到数字中频回波信号，之后进行数字正交解调得到基带回波信号；然后分别与两路正交参考信号混频，最后对混频后的四路信号分别进行离散时间傅里叶变换(Discrete Time Fourier Transform, DTFT)得到目标散射矩阵估计值。

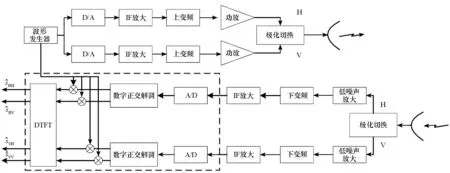
图1 基于数字去斜处理的同时全极化雷达信号处理流程Fig.1 Signal processing of simultaneous polarimetric radar based on digital dechirp processing

设同时全极化雷达发射波形为

(1)

其中，

(2)

Tp为脉冲持续时间，fc为中心频率，γ=B/Tp，B为信号带宽。

雷达水平和垂直极化天线对回波信号同时进行接收，回波信号[6]可以表示为

(3)

为了简化公式表达，定义两组符号如下

w(fc,t)=exp(j2πfct)

(4)

(5)

其中，“*”表示复数共轭。将式(4)和式(5)代入式(3)，假定雷达收发天线和通道特性理想，则有R∝I,T∝I，I为单位阵。忽略幅度因子，式(3)可得

(6)

回波信号经过下变频处理得到中频信号uI(t)，其表达式为

(7)

其中，fI为中频频率。对雷达中频回波信号uI(t)以采样率fs采样，然后进行数字正交解调得到基带回波信号

n=1,2,…,N

(8)

式中：N为离散回波采样点个数。

数字去斜处理在数字域将回波信号与同时宽的参考信号混频，参考距离与雷达接收波门中心一致。设参考距离对应的时延为t0，则两路参考信号为

(9)

回波信号与参考信号混频后得到的差频信号为

(10)

式中，“†”表示复数共轭转置。当时宽带宽积BTp≫1时，有[27]

(11)

式中，f为傅里叶变换中的频率。

基于式(11)，式(10)可以近似为

(12)

1.2 数字去斜处理残余视频相位项的补偿

对式(12)进行DTFT，可得

(13)

(14)

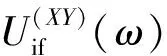
(15)

其中，φXY为目标极化散射矩阵各元素真实相位值。

2 系统频率偏差对全极化测量的影响

2.1 雷达中频偏差对全极化一维像峰值位置的影响

雷达中频信号经过ADC采样后进行数字正交解调得到数字基带回波信号。在实际系统中，中频频率与标称频率存在一定的偏差，该偏差经过数字正交解调后会在基带信号上叠加一个与频偏相关的单频项。由于水平极化接收和垂直极化接收处理过程一样，为了简化表达，本文以水平极化接收为例进行分析。

水平极化接收通道接收的目标中频回波采样信号为

(16)

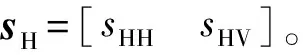
(17)

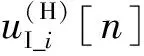
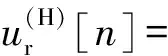
(18)

与式(8)相比，式(18)多了与ΔfI相关的单频项w*(ΔfI,n/fs)，n的取值范围由矩形窗函数确定。与本地数字参考信号混频后得到

(19)

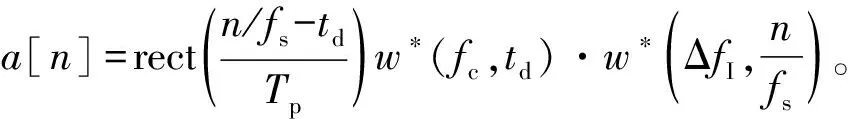
基于上节分析，当时宽带宽积BTp≫1时，差频信号近似为

(20)

2.2 A/D采样频偏对全极化测量相位的影响

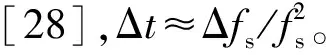
(21)

其中，Δt0与目标相对波门中心位置相关。同样地，以水平极化接收通道信号为例进行分析。 假设采样频率偏差为Δfs，则式(9)变为

(22)

(23)

式(23)与式(12)相比，除了时延发生变化外，还引入了二次相位项

(24)

(25)

令m=「n-N/2⎤，「·⎤表示上取整运算。代入上式，并对三角函数进行级数展开得到

(26)

当Δt/fs≪1时，式(26)近似为

(27)

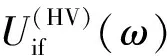
(28)

以上分析表明，采样频率偏移不仅会引起全极化一维像峰值位置的整体偏移，还会对极化散射矩阵估计值的相位产生影响，具体表达如式(27)和式(28)所示。时宽带宽积越大，采样频率越不稳定，该相对相位差越大。特别地，对于采用大时宽带宽积的宽带雷达，若信号时宽带宽积BTp=4×104，采样频率稳定度为10-5，该相对相位差可达24°，这将对目标的极化散射特性产生影响。因此，需要采取措施消除该相位差。

2.3 校准方法

为了校正峰值位置偏差和相位误差，基于上节推导的理论结果，以金属球作为定标体，分别对中频频偏和采样频偏进行校准，校准过程如下：

Step1：对金属球两路中频回波数据分别进行数字去斜处理。

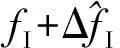
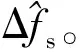
3 仿真分析与实测数据验证

3.1 仿真分析

3.1.1 采样频率偏差对相位测量的影响

对X波段雷达，假定脉冲持续时间为20 μs，中频采样率为fs=1.6 GHz，当信号时宽带宽积在[103,5×104]内变化时，分别计算采样频率偏差Δfs为0.5 kHz、1 kHz、2 kHz、5 kHz、10 kHz和20 kHz时引入的相对相位差，如图2所示。图中结果显示，若采样频率足够稳定(Δfs/fs<2×10-6)，在给定的信号时宽带宽积范围内，相位差在6°之内；若采样频率稳定度在10-5量级，BTp=104条件下，该相位差可达十几甚至几十度，对极化测量结果影响较大。

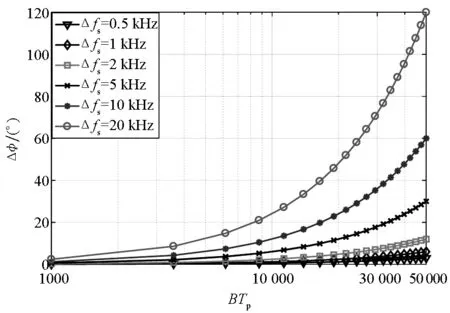
图2 不同时宽带宽积、不同采样频偏条件下相位差的变化Fig.2 Phase error with different time-bandwidth products and different sampling frequency offsets

3.1.2 中频频偏与采样频偏对全极化测量结果的影响及校准

仿真参数设置如下：信号时宽Tp=20 μs，带宽B=500 MHz，中频频率fI=300 MHz，采样率fs=1.6 GHz，中频频率偏移ΔfI=15 kHz，采样频率偏移Δfs=40 kHz，经过数字去斜处理后结果如图3所示。

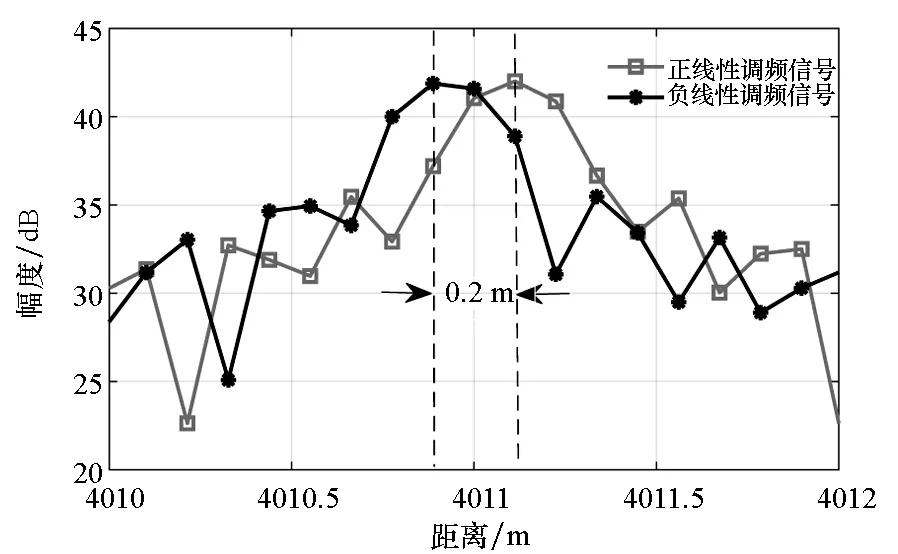
(a) 校准前一维距离像幅度(a) Amplitude of high resolution range profiles before calibration

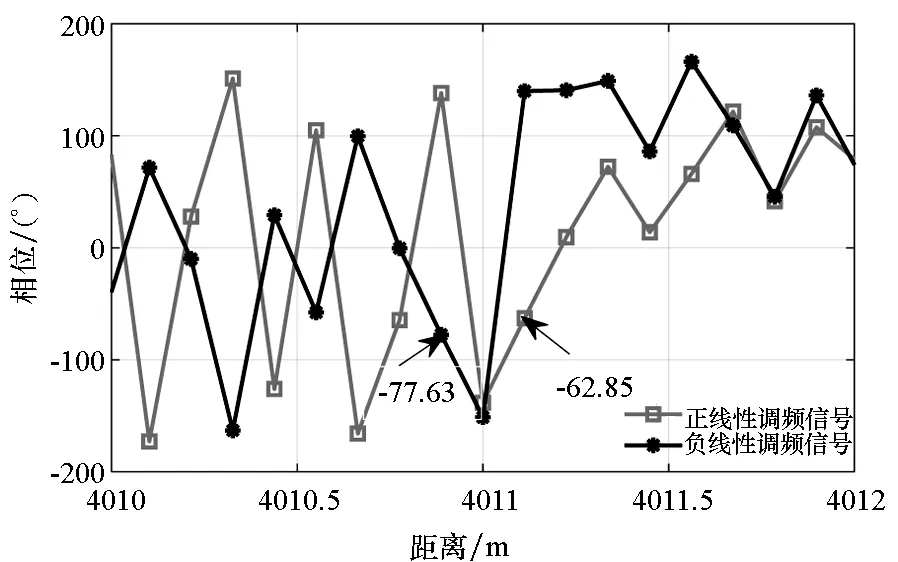
(b) 校准前一维距离像相位(b) Phase of high resolution range profiles before calibration图3 雷达系统频率偏差对全极化测量的影响Fig.3 Influence of frequency deviation of radar system on full polarization measurement

与理论分析结果一致，中频频率偏差引起了正负线性调频信号去斜处理之后不同极化通道目标散射点位置的左右偏移，偏移量约0.2 m，依据3.1节分析，估计中频频率偏移约为16.67 kHz；采样频率偏差引入了约0.26 rad(14.78°)的相位差，依据式(27)和式(28)，估计得到采样频偏约为39.435 kHz，此时采样频率稳定度为2.464 7×10-5。分别对中频频率和采样频率偏差进行校准，经过校准之后得到的结果如图4所示，校准之后，峰值位置重合，剩余相位差约为0.003 5 rad。

通过上面的仿真发现，利用峰值位置估计中频频率偏差的精度与傅里叶变换点数相关，在实际工程实现中，需要结合具体的应用设置合适的点数。

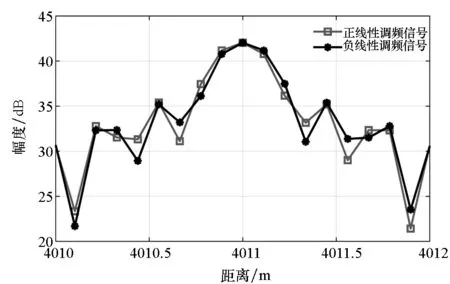
(a) 校准后一维距离像幅度(a) Amplitude of high resolution range profiles after calibration

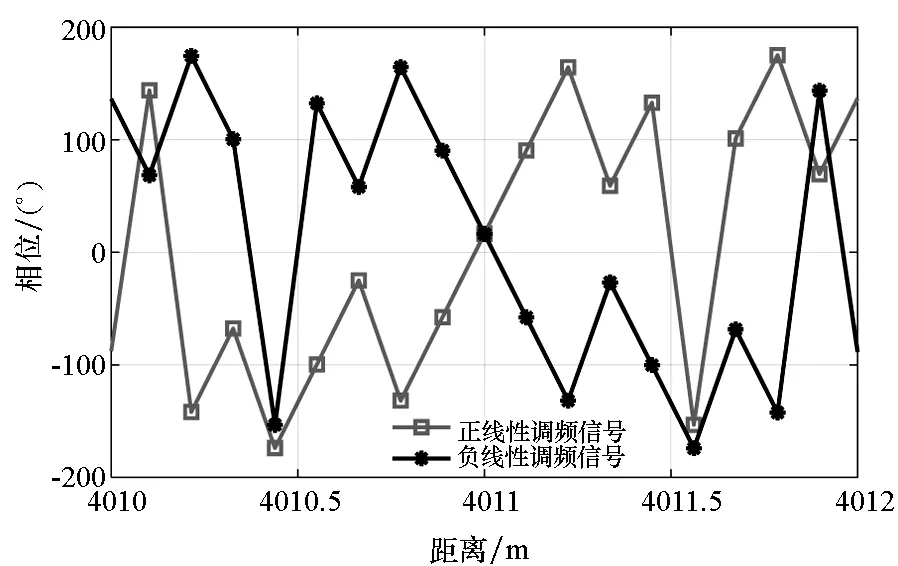
(b) 校准后一维距离像相位(b) Phase of high resolution range profiles after calibration图4 校准雷达系统频率偏差之后全极化测量结果Fig.4 Measurement of PSM after calibration

3.2 实测数据验证

实验使用安捷伦公司的M9330任意波形发生器生成两路正负线性调频中频回波信号，经过M9730A完成中频信号数字化后，进行数字正交解调，然后与参考信号进行混频、DTFT得到金属球目标的极化散射矩阵估计值。实验使用波形参数为：B=500 MHz，Tp=20 μs，中频频率fI=300 MHz，采样率fs=1.6 GHz。两路中频回波信号经数字去斜处理后结果如图5所示。

图5 校准前HH和VV通道一维距离像Fig.5 High resolution range profiles of HH and VV channels before calibration

图5结果显示两路调频斜率相反的LFM回波信号经过数字去斜处理后频谱峰值不重合，表明系统中频存在偏差。根据峰值位置差(0.112 2 m)估计中频频偏约为9.35 kHz。校准中频频偏之后的结果如图6所示，两个峰值位置重合。

图6 校准后HH和VV通道一维距离像Fig.6 High resolution range profiles of HH and VV channels after calibration

基于中频频率偏差校准之后的结果，表1给出了校准采样频率偏差前后金属球主极化元素的相位变化。校准采样频偏之前，相位差约为0.392 rad(22.48°)，依据式(27)和式(28)，估计得到采样频偏约为59.94 kHz。校准采样频偏之后，峰值处剩余相位差约为0.022 rad，即1.255°。

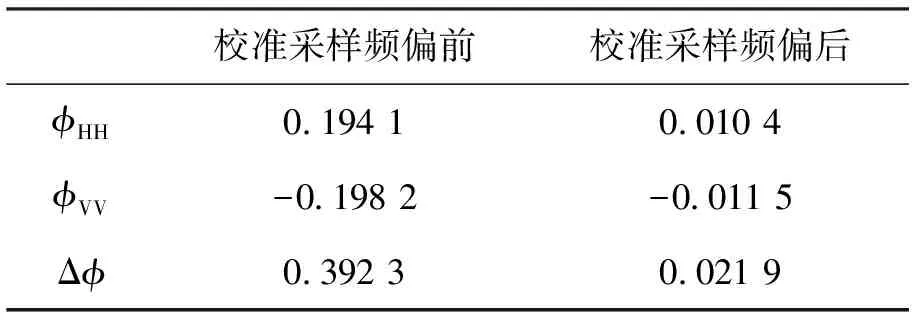
表1 金属球主极化元素采样频偏校准前后相位结果

4 结论

本文分析了采用正负线性调频信号的同时全极化测量雷达系统频率偏差对目标极化散射矩阵的影响，并提出了中频偏差和采样频偏的联合估计及校准方法。仿真和实测数据分析表明：本文提出的校准方法能有效校准雷达系统频率偏差的影响。同时全极化测量除受通道、天线、波形等因素的影响之外，对系统频率偏差的校准也应作为同时全极化雷达极化校准的内容，而本文研究无疑为同时全极化雷达极化校准提供了技术支撑。本文讨论的频率偏差是一个微小量，要求定标体PSM两列元素存在相位相同的项，且假定雷达天线和通道特性理想，而在实际校准过程中，上述条件很难满足，因此后续需要结合雷达系统的其他非理想因素，分析各项误差产生的机理，提出更完善的误差校准方法。同时，由于该误差项与雷达波形存在相关性，后续需要结合其他同时全极化波形进行系统频率偏差的影响分析。