新体制导航信号下I/Q幅相不一致对接收机测距零值的影响分析*

李柏渝，唐小妹，王耀鼎，刘 哲

(国防科技大学 电子科学学院， 湖南 长沙 410073)

频率规划是导航接收机总体设计中的重要步骤，有实信号采样与复信号采样两种方式可选，目前以实信号采样方式为主。

当信号带宽较窄时(如GPS L1频点信号)，中频频率fIF和采样频率fS的选择较为容易。随着导航系统的现代化，新型导航信号的频谱越来越宽，其中E5频点信号主瓣宽度达到50 MHz以上。实信号采样方式下，为保证足够的数字域过渡带宽，fS要取120 MHz[1]，甚至是250 MHz[2-3]；若采用复信号采样方式，则fS可降至65.469 MHz[4]。由此可见，随着新型信号带宽的增大，复信号采样的优势越发明显。

由于存在I/Q幅相误差，复信号采样的应用受到了一定的限制。已有文献定量分析了I/Q幅相误差对导航接收机等效载噪比[4-6]和测量零值的影响[7-8]，但上述模型将部分环节理想化，与实际信道特性不符。文献[9]统一考虑信道非理想和I/Q幅相误差，给出了二者共同影响二进制相移键控/正交相移键控(Binary Phase Shift Keying/Quadrature Phase Shift Keying, BPSK/QPSK)信号测距精度与零值的一般性定量分析模型，但并不适用于二进制偏移载波(Binary Offset Carrier, BOC)信号。

针对上述现状，本文将文献[9]中的模型推广至BOC信号体制，得到了任意的I/Q幅相误差和信道非理想特性共同影响BOC信号测量零值的分析模型，并分析了频域抗干扰场景下，二者共同引起的伪距零值变化。本文的分析方法可用于指导复信号采样的高性能BOC信号接收机设计。

1 导航接收机I/Q非理想分析模型修正

文献[9]基于图1中的模拟正交下变频信道模型，分析了I/Q幅相误差对零值的影响。

图1 模拟正交下变频信道模型Fig.1 Model of analog orthogonal down conversion channel

文献[9]在分析中将频率为fLO的模拟本振下变频的幅度误差ae-LO和相位误差θe-LO在Q通道滤波器hQ(t)中统一考虑，得到了正交下变频后的信号分量ys(t)为：

ys(t)=xL(t)*hIL(t)+j×xL(t)*hQL(t)

(1)

其中：xL(t)、hIL(t)与hQL(t)分别为图1中输入信号x(t)、I通道滤波器hI(t)与hQ(t)的等效低通信号，j为虚数单位，*为卷积运算符。

由于存在I/Q幅相误差，ys(t)中含有镜频分量(其与有用信号的比值可用镜频抑制比表示)，可能会对信号接收造成影响。文献[9]考虑了最恶劣的情况(镜频分量的频谱经过延拓后与信号分量的频谱几乎重叠)，指出：由于卫星与导航接收机非同源，且存在多普勒，镜频分量与信号的频谱不可能完全重叠(一般至少存在千赫兹级的频差)；因此可将镜频处的信号和噪声分别等效为匹配谱干扰及加性噪声，二者会影响等效载噪比，但不影响测量零值。

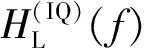
(2)

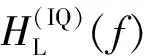
(3)

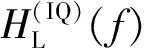
(4)

(5)

令ε[HIL(f)]是信道等效低通滤波器为HIL(f)时的零值估计偏差。定义I/Q幅相误差引入的零值变化Δε(IQ)为：

(6)

由式(6)知,通常情况下，I/Q误差越大，Δε(IQ)越大。

2 I/Q幅相误差影响BOC信号零值的分析

2.1 在BOC信号下的分析

BOC调制被广泛应用于各导航系统的现代化信号，以实现军民码频谱分离。各导航系统提供公开服务的BOC信号类型如表1所示[10-13]。

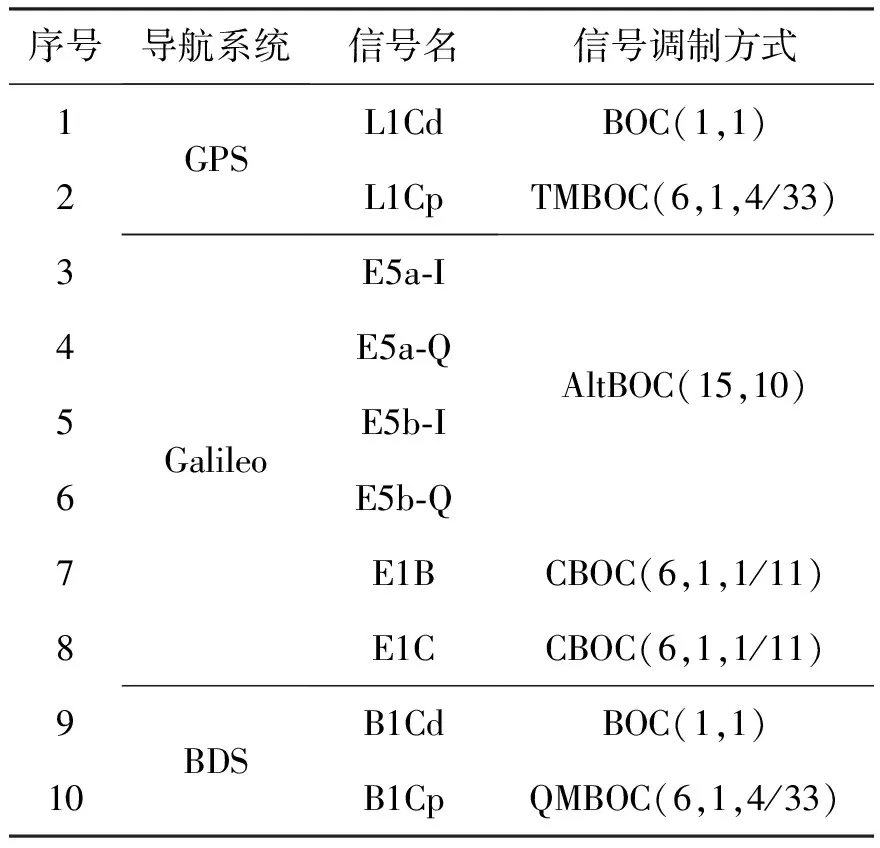
表1 各导航系统中公开服务的BOC信号列表

由表1可知，目前提供公开服务的BOC信号调制方式为AltBOC(15,10)、BOC(1,1)、TMBOC(6,1,4/33)、QMBOC(6,1,4/33)与CBOC(6,1,1/11)。由于将TMBOC(6,1,4/33)信号、QMBOC(6,1,4/33)和CBOC(6,1,1/11)信号当作BOC(1,1)信号进行接收，仅分别引起0.56 dB、0.56 dB和0.41 dB的信号损耗(某地面站高精度导航接收机即采用该接收方案)，因此本文对于公开服务BOC信号仅分析BOC(1,1)与AltBOC(15,10)这两种调制方式。

本文重点分析I/Q幅相误差对提供公开服务的BOC信号的影响，对其他BOC信号的影响可参照该方法分析，本文不详细展开。文中分析均对f0(1.023 MHz)进行归一化。

2.1.1 BOC(1,1)信号下的理论分析

BOC(1,1)信号可采用匹配接收并用Bump-Jump方法进行辅助。考虑信道非理想特性，此时的零值估计偏差ε满足[14]：

(7)

其中，A(f)与φ(f)分别为信道等效低通滤波器的幅频响应和相频响应，GBB(m,n)(f)为BOC(m,n)信号归一化的功率谱密度函数，化简文献[13]与文献[14]中的GBB(1,1)(f)，得：

(8)

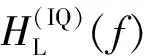
(9)

其中：

(10)

(11)

(12)

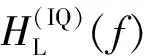
(13)

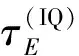
2.1.2 对AltBOC(15,10)信号的理论分析

由于上下两个边带信号在频谱上距离较远，通常导航接收机会将AltBOC(15,10)信号的上下边带当作两个独立的QPSK信号分别进行接收。此时可使用本文对文献[9]的修正模型分析I/Q幅相误差对两个QPSK信号零值的影响。

2.1.3 对其他BOC信号的理论分析

采用副载波消除法进行接收时，授权的BOC(10,5)信号的零值估计偏差ε满足[14]：

(14)

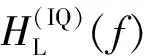
(15)

其中，

(16)

(17)

(18)

在其他BOC信号下，I/Q幅相误差对测量零值的影响与具体的接收方式相关。本节只给出BOC(10,5)在副载波消除法下的分析结果，在其他信号调制方式和接收方式下的分析，可参照本节分析方法进行。

2.1.4 数值仿真

限于篇幅，本文仅对BOC(1,1)进行仿真。

1) I/Q通道之间有三次曲线相位差。根据实际测试结果，大量滤波器的群时延具有二次曲线的特性[15]，其相位为三次曲线。在数值仿真时考虑相对简单的情况，HIL(f)与HQL(f)均是幅度为1的二次曲线群时延滤波器，其相频φIL(f)与φQL(f)的表达式分别为：

(19)

(20)

其中，κE表示HIL(f)的失真程度，κIQ表示I/Q相位误差的大小。

将式(19)与式(20)代入式(3)化简后得：

(21)

图2给出了κE为0时，不同D下，以1/80为步进，κIQ从0到1/8时(κIQ为1/8时对应的相位误差为π/6)对应的Δε(IQ)，图中的Tc表示码片。

图2 不同的D与κIQ引起的Δε(IQ)Fig.2 Δε(IQ) caused by various D and κIQ

由图2可知：

①即使HIL(f)为理想低通滤波器，I/Q幅相误差也会引入零值变化Δε(IQ)，这说明I/Q幅相误差本质上就是信道非理想特性的一种。

② I/Q误差κIQ越大，Δε(IQ)越大，这与理论分析吻合。

③对于同样的κIQ，D越小，Δε(IQ)越大，这说明I/Q误差下，大的相关间隔更稳健。

2) I/Q通道之间有三次曲线相位差，再叠加上巴特沃兹型滤波器的幅度误差。参照文献[16]，考虑到ω= 2πf，最平坦的巴特沃兹低通滤波器带内幅频特性满足：

(22)

其中，PLR(f)表示在频率为f处相比于中心频率处的功率损耗，N是滤波器的阶数，fc为通带截止频率(此处取b)，1+a2为功率损耗比。如选择通带最大损耗为3 dB，则a=1。

为仿真简便，取HIL(f)为理想低通滤波器，HQL(f)的幅频响应AQL(f)满足巴特沃兹低通滤波器，相频响应ΦQL(f)满足三次曲线，分别为：

(23)

(24)

其中，aIQ表示I/Q幅度误差的大小。

图3给出了D取0.5(由前文知该参数更稳健)，N=7时，κIQ从0变化至1/8，aIQ(aIQ=0表示无幅度误差)对应的Δε(IQ)。

图3中的3条曲线基本重叠在一起，说明巴特沃兹低通滤波器对应的I/Q幅度误差导致零值变化较小。造成这一结果的主要原因是越大的幅度误差越靠近边带，而BOC(1,1)信号在边带的功率谱较小，因此大的幅度误差造成的影响也相对较小。

图3 巴特沃兹滤波器下，不同κIQ与aIQ引起的Δε(IQ)Fig.3 Δε(IQ) caused by various κIQ andaIQ when Butterworth filter is applied

3) I/Q通道之间有三次曲线相位差，再叠加上切比雪夫型滤波器的幅度误差。如取HIL(f)为理想低通滤波器，HQL(f)的幅频响应满足切比雪夫低通滤波器，相频响应ΦQL(f)满足式(24)，参照文献[16]，AQL(f)满足：

(25)

其中，TN(f)为关于f的N阶切比雪夫多项式。

图4给出了D取0.5，N=7时，κIQ从0变化至1/8，aIQ分别为0、0.5、1、2、3时所导致的Δε(IQ)。

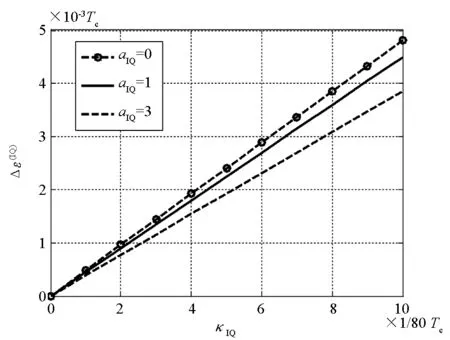
图4 切比雪夫滤波器下，不同κIQ与aIQ引起的Δε(IQ)Fig.4 Δε(IQ) caused by various κIQ andaIQ when Chebyshev filter is applied

由图4可知，在同样的通带最大幅度误差和相位误差下，相比巴特沃兹型滤波器，切比雪夫型滤波器造成的影响更加明显。主要原因是切比雪夫型滤波器在通带内是等波纹波动，信号在通道内的功率谱都受到了幅度误差的影响。

2.2 结合频域抗干扰场景的推广

2.2.1 理论分析

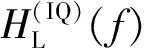
在干扰场景下，频域抗干扰算法通过在频域上对干扰频谱置0的方法抑制干扰，假如干扰存在的频率范围为[f1,f2]，干扰抑制滤波器Hjam(f)的表达式为：

(26)

(27)

(28)

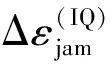
2.2.2 数值分析

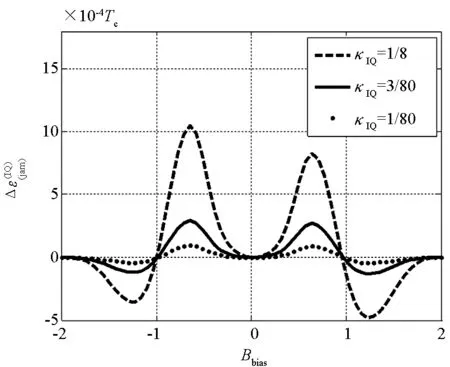
图5 不同Bbias与κIQ下的 under various Bbias and κIQ

图6 不同的Bbias与κE下的 under various Bbias and κE

图5与图6的分析如下：

3 软件接收机仿真

3.1 仿真条件设置

在软件接收机上对理论分析进行仿真验证，仿真过程如图7所示。首先，由软件接收机生成中频复采样BOC(1,1)信号；其次，将其分别与I/Q两路信道滤波器特性相乘；再次，做快速傅里叶逆变换，得到通过滤波器后的信号；然后，对该信号进行下变频与跟踪，统计跟踪稳定后的码相位均值，即得测量零值。需要重点说明的是：在仿真试验时并未生成干扰信号，但根据不同的干扰特性，将信道滤波器对应干扰位置的幅频置0，以模拟频域抗干扰场景。

图7 软件接收机实现结构Fig.7 Implementation structure of software receiver

仿真时采用两组滤波器(分别称为A组与B组)均为真实滤波器。每组内的I通道与Q通道滤波器采用相同设计，但存在I/Q幅相误差；两组滤波器有较明显的差别，A组滤波器的非理想特性较严重，B组滤波器比较接近理想带通。对两组滤波器均进行22次仿真试验，其中1次模拟无干扰场景，其他21次模拟干扰场景。在模拟的21个干扰场景中，第1个场景和第21个场景信道滤波器幅频置0的频率范围分别为[-2,-1.8]和[1.8,2]；其余19个场景下信道滤波器幅频置0的频率范围为[Bbias-0.2,Bbias+0.2]，Bbias以0.2为步进，取值从-1.8至1.8。这21个场景共同模拟1个以Bjam为0.4的干扰，在不同位置时对测量零值造成的影响。仿真时，信号载噪比为60 dB-Hz，积分时间T取1 ms，码环带宽设为0.5 Hz，相关间隔D=0.5。

3.2 仿真结果

图8 不同Bbias与滤波器下仿真值对比Fig.8 Comparison of the simulation value of under various Bbias and filters

图9 不同Bbias与滤波器下理论值与仿真值误差Fig.9 Deviation of the theoretical value and the simulation value of under various Bbias and filters

对图8与图9进行分析：

4 结论

本文的意义如下：

1)建立了I/Q幅相误差影响BOC信号接收机测距零值的模型，本文模型适用于任意的信道非理想特性与I/Q幅相误差；

2)软件接收机仿真结果与理论分析高度吻合，说明本模型正确揭示了信道非理想特性与I/Q幅相误差影响BOC信号零值的规律；

本文的分析结论可用于指导高性能复采样BOC信号导航接收机的设计。