备件保障效能动态评估方法*
董骁雄,车 飞,陈云翔,何 桢,朱 强
(1. 空军工程大学 装备管理与安全工程学院, 陕西 西安 710051;2. 空军编余飞机储存中心, 河南 平顶山 467300;3. 空军研究院, 北京 100085; 4. 空军指挥学院, 北京 100089)
备件是部队“两成两力”(成建制、成体系形成作战能力和保障能力)建设的物质基础,对装备平时、战时保障都有深远影响[1]。在当前武器装备日益复杂、更新换代速度不断加快、备件价格急剧攀升的背景下,备件保障工作直接影响着装备完好率、任务成功性以及寿命周期费用,其重要性毋庸置疑[2]。
针对备件保障效能评估问题,国内外学者开展了大量研究,主要分为两类:一是对备件保障效能评估指标体系构建的研究,如文献[3-4];二是采用多种评估方法对备件保障效能进行评估,如数据包络分析(Data Envelopment Analysis, DEA)方法[5]、层次分析方法[6]、灰色关联分析方法[7]、集对理论[8]、效用函数方法[9]等,上述方法在对备件效能指标的观测值进行融合的过程中,并未利用效能评估过程所包含的趋势信息,属于静态评估,相应的效能指标只能反映当前的保障态势,无法描述备件保障水平的发展趋势。而保障效能趋势能够较为准确地反映一段时间内的备件保障水平的变化情况,将有助于为决策者制定备件保障长期计划提供科学依据。在备件保障效能评估中引入这一信息,可以提高备件保障效能评估的合理性。目前,对于备件保障效能的动态评估的研究还比较缺乏,在效能评估领域,还没有研究灰色聚类-粗糙集(Grey Clustering-Rough Set, GC-RS)和集对分析(Set Pair Analysis, SPA)方法组合使用的文献。
1 备件保障效能指标体系构建
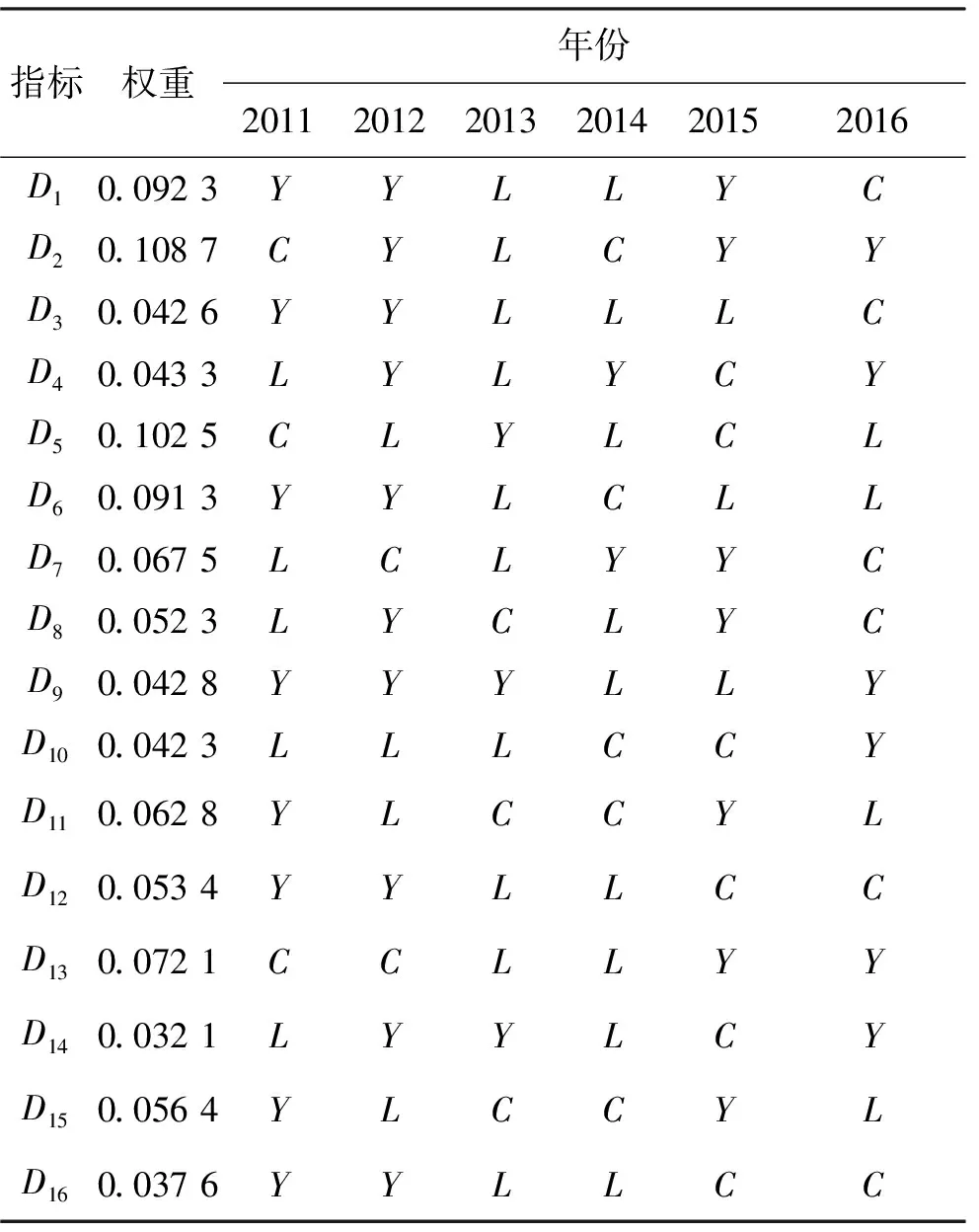
综合考虑组织管理对备件保障效能的深层次影响,结合航空兵部队备件保障任务要求,将影响备件保障效能的因素划分为任务指标、经费指标和管理指标3个一级指标。并参照文献[8,10],在遵循体系化、唯一性、客观性、严格性和前瞻性原则的前提下,采用Delphi法得到以下16个二级指标,如表1所示。

表1 备件保障效能指标集
2 备件保障效能动态评估方法
2.1 基于GC-RS的属性权重确定方法
确定权重的方法主要包括主观赋权方法和客观赋权方法,主观赋权法有层次分析(Analytic Hierarchy Process, AHP)法、 Delphi法等,客观赋权法有粗糙集方法[11]、灰色聚类方法[12]和熵权法[13]等。其中:主观赋权法具有一定的主观随意性,影响决策的准确性和可靠性;客观赋权法是充分利用原始数据计算权重的方法,虽避免了赋权的主观随意性,但是在计算权重时存在相应的不足。
灰色聚类方法在处理信息时一般没有系统信息的损失,但无法确定基于客观信息的系统各属性的权重,并且采用灰色评价时通常需要提供先验的权重分配。粗糙集则不需要提供先验信息,并且提供了确定权重的方法,但它在处理数据时采用区间划分方法忽略了较多的系统信息。将二者的优缺点互补,采用灰色聚类-粗糙集组合方法确定各指标的权重。
假设评价对象用Xi(i=1,2,…,n,n为评价指标个数)表征,其m个指标构成的集合为F=(p1,p2,…,pm)T。
权重确定的步骤为:
步骤1:确定需要处理的样本对象,抽取样本指标数据。
记样本j的指标值为Xj=(X1j,X2j,…,Xmj)(j=1,2,…,n)可以构造出矩阵X:
步骤2:采用灰色聚类方法分析样本指标聚类。
1)归一化处理,为了进行聚类分析,需要使数据规格化,即具有统一的量纲和数量级,对指标值Xj=(X1j,X2j,…,Xmj)(j=1,2,…,n)归一化处理得到标准化矩阵。
2)建立灰色关联关系,确定样本之间的灰色关联度rij。对于系统行为序列Xj=(X1j,X2j,…,Xmj)(j=1,2,…,n),则Xi,Xj(i≤j)的灰色绝对关联度rij[7-9]为:
(1)
式中:
(2)
(3)
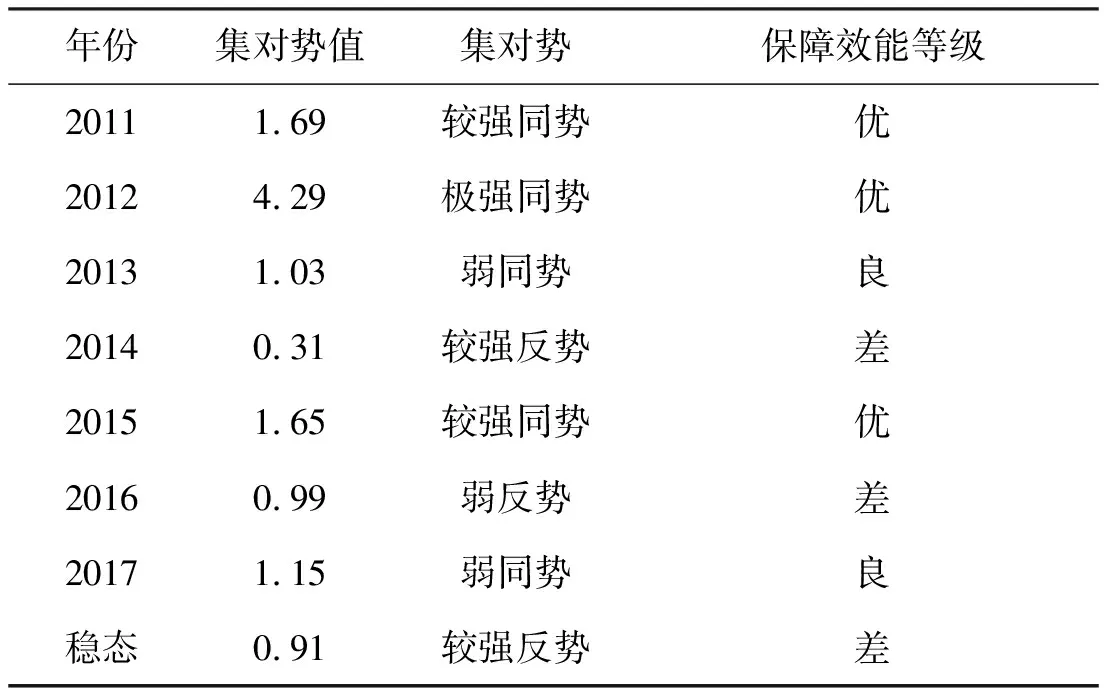
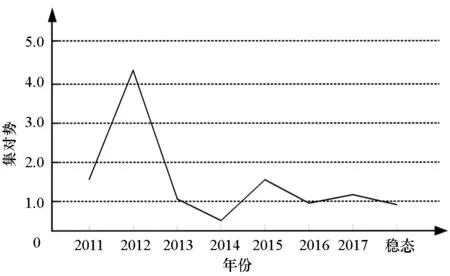
灰色绝对关联度rij具有以下性质[10]:① 0 这样就可以得到如下三角矩阵: 称这个矩阵为样本的灰色关联矩阵。采用聚类分析[7]中的直接聚类法进行聚类,将R中除了对角线元素以外的所有互不相同的元素按照从大到小的顺序编排,并表示为: 1=θ1>θ2>θ3… (4) 取聚类阈值θ=θk∈[0,1],当 rij≥θk(i≠j) (5) 则认为Xi和Xj具有相同特性并将其分为一类。聚类阈值θ的取值不同,分类结果也就不同,θ越接近1,分类就越细。 设B1,B2是聚类阈值为θk时的两个类,若 B1∩B2≠∅ (6) 则称它们是相似的。将所有相似的类合并成一类,最后得到的分类就是聚类阈值为θk时的等价分类。 3)根据灰色关联矩阵确定适当的阈值范围ak(k=1,2,…,p),在各阈值范围内进行分类,其中p为由阈值范围确定的置信水平个数。以阈值范围的高端为标识ak(k根据阈值的大小确定),记录采用不同阈值范围时各类包含的元素的名称及个数,分别记为Ci(i=1,2,…,k)。 步骤3:采用粗糙集方法确定指标ak(k=1,2,…,p)的综合重要度。 1)删除指标Xi(i=1,2,…,n),重复步骤2,根据在未删除指标时确定的阈值对其重新分类,并将分类结果与原始分类对比,初步判定指标Xi,对分类的影响。 2)采用粗糙集理论求得指标值Xi(i=1,2,…,n)在某一个置信水平ak下的重要度。 定义2 (信息系统)S=(U,A,V,f),其中U是对象的非空有限集合,A=C∪D是属性的非空有限集合,其中C是条件属性的非空有限集,D是决策属性的非空有限集合,V是A的属性值集合,且C∩D≠∅,则C与D的依赖程度为: (7) 根据式(3)可得某一置信水平ak下,指标l的重要度: SigCDak(Cl)=γC(D)-γC-Cl(D) (8) 式中:条件属性C为样本指标集合;D为决策属性集,指考察样本的灰色聚类标识。 考虑进行灰色聚类时,不同的阈值水平也是不同的置信水平,将p个置信水平结合起来考虑,各指标的综合重要度为: (9) 根据综合重要度的大小确定指标l的权重: (10) 集对分析是从同、异、反三个方面研究两个集合之间的相互关系的系统分析方法。基本思想是将某一问题中的确定和不确定特性作为一个系统,分析两者之间的关系,并通过联系度的概念进行数学描述。 对于两个给定集合组成的集对{A,B},在某个具体问题W中进行分析,共得到N个特性,其中S为集对相同特性数,Q为集对对立特性数,P为集对中既不对立也不相同的特性数,那么此集对的联系度通用表达式[14]为: (11) SPA理论用于备件保障效能评估时,可将保障效能评估指标体系和保障效能状态等级视为一个集对。采用集合A表示保障效能评估指标体系,集合B表示保障效能状态等级,则集合A和集合B可构成保障效能评估集对H= (A,B)。在此基础上,将2.1节确定的指标权重引入SPA,依此来描述备件保障效能联系度。 表2 保障效能评估等级 由此,假设在t时刻,16个备件保障效能评估指标中有Yt个指标的保障效能等级为优(Y),Lt个指标的保障效能等级为良(L),Ct个指标的安全等级为差(C),且满足Yt+Lt+Ct=16。根据式(4),将16个评估指标仍按优(Y)、良(L)、差(C)3个等级进行排序编号,且各评估指标在t时刻重新排序后所对应的权重为wk(t),则t时刻的保障效能动态联系度可表述为式(12)[15]。 (12) 当联系度μ=a+bi+cj中的c≠0时,同一度a与对立度c的比值a/c称为所论集对在指定问题背景下的集对势,等价于Y/C,即 (13) 进而定义集对同势为: (14) 集对反势为: (15) 集对均势为: (16) 系统的能力状态是动态变化的,从联系度中差异度i的不同取值可以看出,系统的态势也是一个动态变化的过程,但在一定条件下会趋于一个稳态值。随着时间的改变,条件也发生了变化,态势也随之变化。集对势是以shi(H)=1为均势,是同势与反势的分界线。为进一步说明备件保障效能变化趋势,根据评估指标的3个等级(Y,L,C)相关信息,按照排列组合的原理,将备件保障效能的动态变化情形进行排序,结果见表3。 表3 备件保障效能等级排序 根据表3中保障效能动态变化趋势特点,备件保障单位可根据不同的变化趋势采取相应的预防对策措施,有针对性地减少和避免对保障效能有影响的危险。 若集对{A,B}在(t,t+τ)期间(τ为变化周期)原有指标值的同异反关系发生了变化,有的指标值保持不变,而有的则发生了变化。不妨设在t+τ时刻,集对中原有的St个相同特性中仍有St1个相同,St2个变为既不相同也不对立,St3个变为相互对立(St1+St2+St3=St),则St在(t,t+Δt)周期内的转移向量(经规范化处理)为: S=(P11,P12,P13) (17) 同理,可得转移向量P和Q。 在(t,t+Δt)期间的转移矩阵为M,在t+Δt时刻,备件保障效能的联系度为: μ(t+Δt)=a(t+Δt)+b(t+Δt)i+c(t+Δt)j =(a(t+Δt),b(t+Δt),c(t+Δt))·M·(1,i,j)T (18) 依据马尔可夫链的遍历性可知,随着变化周期n的递增,M将趋于稳定,因此,备件保障效能最终会达到一个稳态。根据联系度的归一化要求,联立可得备件保障效能评估稳态值。 (19) 求解此方程便可得到备件保障效能评估稳态值: (20) 以文献[8]中的算例为例作深入分析,由文献[8]的算例得到A、B、C、D、E五个备件保障单位的指标值决策矩阵D。 D=(dkr)m×n 对上述原始决策矩阵进行归一化并采用灰色聚类方法对指标值进行聚类分析,得到灰色关联矩阵F。 设置不同的阈值,得到如表4所示的分类结果。 表4 灰色聚类结果 运用粗糙集方法确定指标Di(i=1,2,…,16)的综合重要度。 删除指标D1“年度总飞行时间”,重复灰色聚类过程,将聚类结果与原始聚类结果比较,初步确定指标D1对聚类的影响程度。 根据综合重要度的定义,运用式(8)~(10)得到指标D1的权重为0.092 3,同理可得D2的权重为0.108 7,D3的权重为0.042 6,D4的权重为0.043 3,D5的权重为0.102 5,D6的权重为0.091 3,D7的权重为0.067 5,D8的权重为0.052 3,D9的权重为0.042 8,D10的权重为0.042 3,D11的权重为0.062 8,D12的权重为0.053 4,D13的权重为0.072 1,D14的权重为0.032 1,D15的权重为0.056 4,D16的权重为0.037 6。 采集到备件基层保障单位(A)2011—2016年各年度的备件保障相关数据,如表5所示,对该单位备件保障效能进行动态评估。 根据式(12)和表3可得出备件保障单位A备件保障效能各年度的联系度为。 表5 备件保障效能评估数据 μ2011=0.479 2+0.237 5i+0.283 3j μ2012=0.596 4+0.264i+0.139 6j μ2013=0.177 4+0.651 1i+0.171 5j μ2014=0.110 8+0.527 7i+0.361 5j μ2015=0.512 1+0.176 7i+0.311 2j μ2016=0.341 3+0.313i+0.345 7j 依据式(13)~(17)可得各年度备件保障效能状态转移矩阵。 假设备件保障效能的年转移矩阵权重相同,得到加权平均转移矩阵: 依据式(18)可以预测2017年的备件保障效能为: μ2017=μ2016·G·(1,i,j)T =0.315 0+0.411 6i+0.273 5j 一般情况下,通过加强备件保障管理,备件保障效果最后会呈现一个平稳态势。假设平均转移概率矩阵G不变,代入式(19)得到备件保障单位A的稳态备件保障效能。 μ=0.287+0.397i+0.316j 利用各年及稳态时联系数表达式计算出集对势值。得到各年集对势值、集对势及保障效能等级,如表6所示,集对势值的动态变化情况如图1所示。 从图1和表6的结果可以看出,备件保障单位A的备件保障水平开始呈现优化态势,随后逐年下降,在势级上发展态势呈现从强同势到强反势的转变,且按照目前的发展趋势最终可以达到集对势水平为0.91的较强反势发展稳态。备件保障单位A应当重视备件保障效能降低的危险,结合表1构建的指标体系查找原因,及时整改。 表6 各年度备件保障效能等级 图1 备件保障效能趋势图Fig.1 Spare parts support effectiveness trend 通过以上结论得到如下启示和建议:提升备件保障效能是一项艰巨和持续的任务,个别时段的高表现和高增长态势并不能完全反映备件保障效能发展的客观水平,要求备件管理部门要时刻关注备件保障效能,确保备件保障效能处于良好态势。 对比文献[8]只能得到备件保障单位的备件保障效能静态评估结果,根据当前备件保障水平,提出建议。提出的方法可以反映备件保障效能在评估时段内的动态变化过程,使决策者能够掌握备件保障单位在评估时段内备件保障水平的发展趋势,为决策者提高备件保障效能提供更加全面灵活的决策依据。 1)针对主观赋权方法和客观赋权方法各自的优缺点,通过引入依赖度和重要度的概念,对指标体系中的指标综合重要性进行了定义,提出基于灰色聚类-粗糙集的指标赋权方法,有效解决了备件保障效能评估指标赋权问题。 2)备件保障效能是一个动态变化过程,将指标权重引入集对分析,提出集对动态联系度的概念,将备件保障效能划分为集对同势、均势和反势,建立基于马尔可夫的集对分析动态模型。该方法可以直接对各时期备件保障效能评估值进行比较,极大方便了决策者对备件保障单位在评估时段内备件保障水平发展趋势的掌握,可以为决策者制定备件保障长期计划提供科学依据。

2.2 基于动态SPA的评估方法
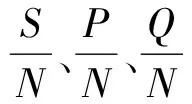

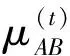
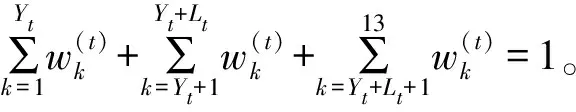

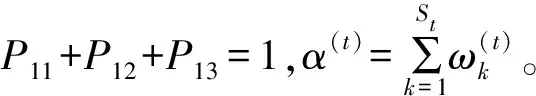
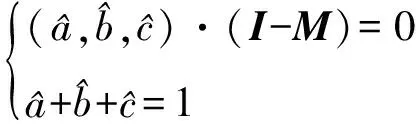

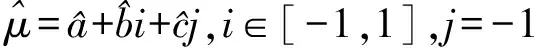
3 实例分析




4 结论

