零压式高空气球球形设计与参数敏感性分析*

杨燕初，张航悦，赵 荣

(1. 中国科学院大学， 北京 100190； 2. 中国科学院 光电研究院， 北京 100094)

高空气球是利用密度小于空气的气体产生的浮力进行飞行，属于临近空间低动态飞行器，具有飞行高度高、速度低、载重大的特点，为高空科学实验研究提供了可靠的平台。目前，高空气球根据内外压差大小可分为零压气球和超压气球，零压气球底部有排气管与大气相通，超压气球则与外界封闭，可以认为超压气球是零压气球在达到升限高度后进一步上升膨胀形成的[1]。零压气球外形为轴对称球形，且目前大多采用了自然形球形的设计。从1782年气球第一次升空之后的150多年里，并没有进行过系统理论性的研究，工程师们依靠直觉选择了诸如正球形、圆柱形及四面体形等形状[1]。直到1939年，Upson提出了自然形气球的概念[2]，规定载荷完全靠子午线方向的球膜应力承担，周向应力始终为零，并且初步推导出气球形状方程。20世纪50年代，研究人员对轴对称自然形高空气球球形系统性地建立了数学模型并数值求解得到一组球形数据，推动了气球球形的研究[3]。1965年，Smalley进一步使用计算机数值求解得到了较为精确和完整的球形数据，并在气球设计中得到了实际运用[4]。之后的球形设计都是在自然形气球的基础上进行改进的，包括Li等在20世纪80年代提出的“混合形”球形[5]以及Yajima等提出的“三维球幅”设计[6]。

自然形球形方程最终可以化简为一组微分方程，在求解方法上，通常是选择标准的Runge-Kutta方法，姜鲁华从提高计算精度方面选择了Gill法[7]，Baginski等利用打靶法得到气球外形数据并指出使用多段打靶法求解部分膨胀状态下球形的可行性[8]。在此基础上，本文提出将多段打靶法与最优化方法中的等式二次规划(Equality constrained Quadratic Programs, EQP)算法结合，进而求解出完全膨胀及部分膨胀状态下的气球母线形状。

高空气球球膜在漂浮高度完全张开，不存在褶皱。在上升过程中，由于球体体积小于漂浮高度时的体积，球膜未完全张开，存在褶皱现象，较小体积时气球底部球膜合拢形成聚束。对球膜褶皱及聚拢的分析涉及改变材料本构关系及褶皱判断等研究[9]，球形设计上通常选择对其进行一定的简化。Smalley引入了“ad hoc”假设，认为未完全膨胀状态下多余的气球球膜均匀地进行轴对称分布，并将球底球膜形成的聚束附加到负载质量中，只计算上方升力气体体积部分气球形状[4]。Baginski等则以同一母线长度处完全膨胀球形与部分膨胀球形截面半径的比值作为球膜密度变化因子，改变部分膨胀状态气球膜密度以使得球体质量在两种状态下都保持恒定，进而忽略褶皱及多余材料的影响，得到气球在部分膨胀状态下球膜同样完全张开的球形[8]。本文亦采用了Baginski的处理方法，将球膜面密度作为变量处理，对部分膨胀状态下气球整体形状进行分析。

1 自然形球形方程推导及数值求解

1.1 自然形球形母线微分方程组推导

气球球膜一般由厚度为20 μm左右的薄膜制成，厚度远小于球体尺度，符合无矩薄壳理论。球形方程推导需使用的相关参数定义见表1，并且取球膜单元进行受力分析，如图1所示，其中单元经放大处理。

表1 相关参数定义

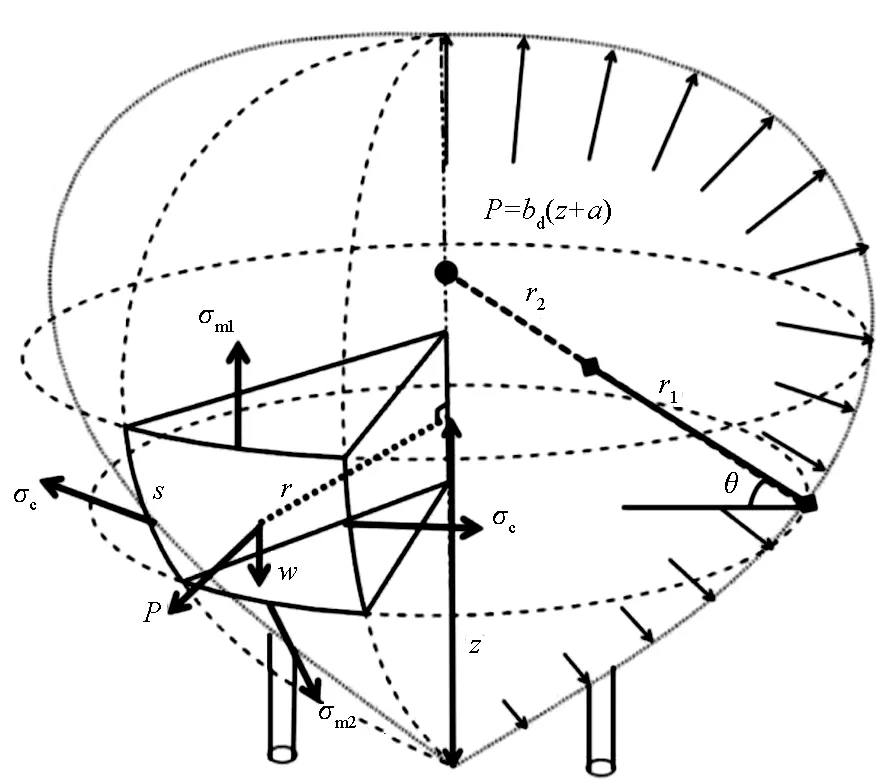
图1 气球球膜单元Fig.1 Balloon film unit

由回转薄壳无力矩理论可知：

(1)

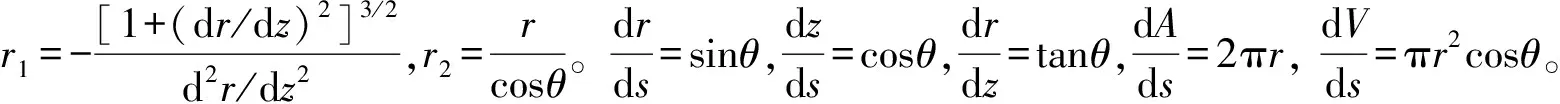
将其代入式(1)并化简得到：

(2)

在截面圆上的总负载T满足T=2πrσm，在弧长方向的改变量d(2πrσm)/ds与周向应力在弧长方向的分量以及膜重存在如式(3)所示关系。

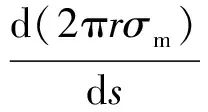
(3)

化简式(3)可得：

(4)

球形参数λ和Σ的定义如式(5)所示，λ、Σ表示了气球负载L及飞行高度(决定bd值)对球形的影响程度。

(5)

自然形气球规定周向应力σc=0。以上各式共同组成球形微分方程组。并使用Simulink搭建仿真程序，如图2所示。

图2 Simulink结构图Fig.2 Simulink structure diagram

1.2 球形方程组数值求解

对于完全膨胀状态的气球，底部起始角度较大，且有边界条件r0=z0=0，rs=0，r0、z0为气球底点半径及高度，rs为气球顶点半径，运用一般打靶法将两点边值问题转换为初值问题进行求解[10]。此时猜测变量为气球母线弧长s及底部起始角度θ0。

(6)

球形底点与顶点两点边界条件表示为g(z(0),z(l))=0，f、g为非线性函数。将边值问题转换为初值问题，设猜测初值为c0。

(7)

打靶法为寻找满足顶点边界条件的c0，通过不断改变初值c0使得式(8)得以满足。

g(c0,y(l;c0))=0

(8)

则z=y(s,c0)为非线性微分方程组的解。

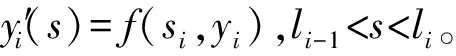
(9)

在以上多段打靶法的基础上，引入EQP算法，即将原始问题转换为一系列等式约束二次规划问题。将多段打靶法融入EQP二次规划问题中，目标函数设为常数，寻找满足打靶法分段约束以及球形边界条件约束的各段起始猜测点。

EQP计算过程中当得到一个迭代点ck，使用ck处的二次规划模型确定ck+1，约束条件为约束函数G(c)在ck处Taylor展开的线性部分。

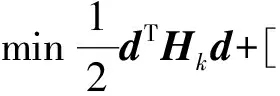
(10)

s.t. [G(ck)]Td+G(ck)=0

(11)

其中,d=c-ck，目标函数O(c)=0；Hk为增广Lagrange函数的Hesse矩阵；步长固定为1，即ck+1=ck+d。

对于上升过程中的气球，按照式(12)改变对应弧长截面的膜密度，以满足在两种状态下气球膜总质量相等的要求。

(12)

式中，r、R分别为完全膨胀状态及部分膨胀状态球形截面圆半径。求解部分膨胀状态时的猜测变量为气球零压点高度a及起始角度θ0。

图3 程序流程图Fig.3 Program flow chart

2 气球设计算例

2.1 工程算例

假定某次飞行任务中，设计指标如表2所示。

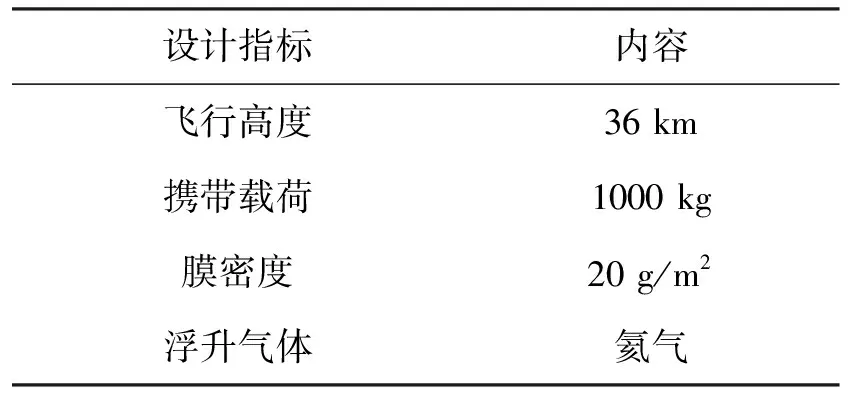
表2 气球设计要求

利用上述算法和流程得到部分参数计算结果，见表3。图4展示了上升阶段及最后稳定阶段气球球形，图5为制作气球时聚乙烯膜裁制尺寸(裁膜曲线纵坐标为气球母线长度，横坐标为由分膜数确定的角度区间所划出的气球截面圆圆弧长度)。

表3 部分参数计算结果

图4 气球母线 图5 裁膜曲线Fig.5 Cutting curve Fig.4 Balloon generatrix

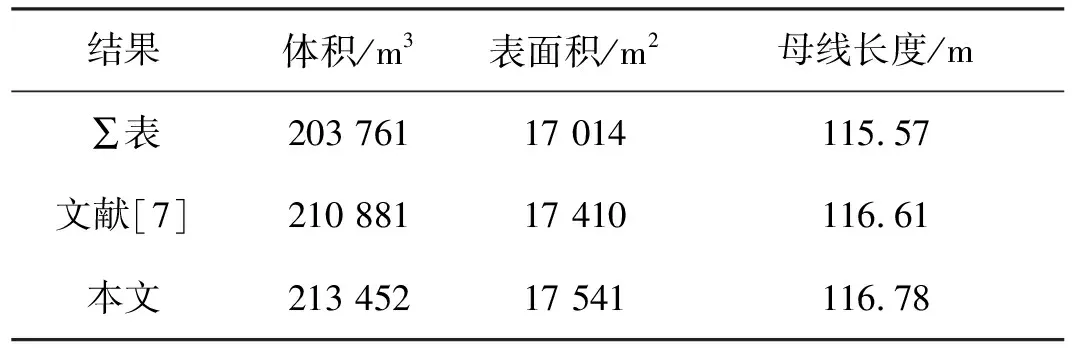
以往工程上根据∑表[1]设计气球，球膜质量按经验系数确定。本文计算结果与∑表[1]设计及文献[7]采用的Gill法计算结果相关参数对比见表4。

表4不同设计方法计算结果对比

Tab.4 Comparison of calculation results

结果体积/m3表面积/m2母线长度/m∑表203 76117 014115.57文献[7]210 88117 410116.61本文213 45217 541116.78

将气球附件质量附加到载荷质量上重新迭代计算得到的气球体积比文献[7]的大1.2%，较以往设计方法更为精确。

上升过程中气球体积、球体高度、零压点高度及单位体积浮力变化曲线如图6所示。

图6 上升过程球形相关参数对比Fig.6 Comparison of shape parameters in the rise process

由图6可以得出，随着气球飞行高度升高，单位体积浮力降低，气球体积膨胀，体积增大速率随高度增加而增加，气球球体高度降低，零压点逐渐下移至底点。

气球上升过程中各高度下气球表面径向应力的计算结果如图7所示。由图7可以得出，球膜径向应力呈现中间小、两边大的分布趋势，在两极趋向于无穷大。这是由于气球两极截面圆半径趋向于零的缘故。在气球结构处理上，常采用双层或是多层头部以减弱气球头部应力集中[6]。文献[8]所提出的“混合形”球形则是假设球膜周向应力并不始终为零，而是在气球的下半部(球底至最大半径处)周向应力为零，在气球的上半部(最大半径处至球顶)周向应力从零单调增加，以至在球顶处周向应力与径向应力相等[7]。据此约束条件求解得到的气球球形能够满足在气球顶部应力趋于有限值[5]。

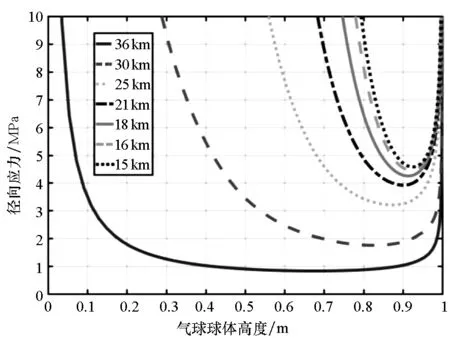
图7 各高度下气球表面径向应力分布Fig.7 Radial stress distribution on the surface of a balloon at various heights

2.2 气球有限元分析及验证

有限元方法也是一种为偏微分方程的边界值问题寻找近似解的数值计算方法，能够对理论计算得到的球形在底部悬挂载荷、膜重力及压力差梯度作用下的应力应变分布进行计算。导入计算所得气球模型，网格选择三维减缩积分四节点M3D4R单元，采用扫掠算法生成结构网格。按照气球所在飞行高度计算(ρa-ρh)·g得到压强差随气球高度变化的梯度系数。计算结果转换在柱坐标下查看。

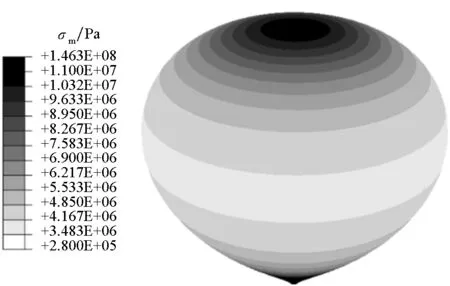
图8 径向应力分布云图(36 km)Fig.8 Radial stress distribution cloud chart(36 km)

结合上述算例，选取典型状态，分别对36 km处(完全膨胀)及30 km处(部分膨胀)气球进行有限元分析，如图8～11所示。结果显示，气球能够维持外形，应力值均保持正值，气球膜处于张紧状态，应力沿高度方向呈环带分布(即同一高度处应力值相同)，据此可判断气球没有褶皱产生。载荷基本靠球膜径向应力承担，并且符合应力从中间向两极逐渐增大的趋势，周向不承受应力(在气球顶部局部区域出现周向应力的原因是仿真中球膜会出现变形导致局部曲率改变，在理论推导中将球膜视作刚体)。因此，有限元分析结果能较好说明所设计气球外形的正确性。

图9 周向应力分布云图(36 km)Fig.9 Circumferential stress distributioncloud chart(36 km)

图10 径向应力分布云图(30 km)Fig.10 Radial stress distribution cloud chart(30 km)

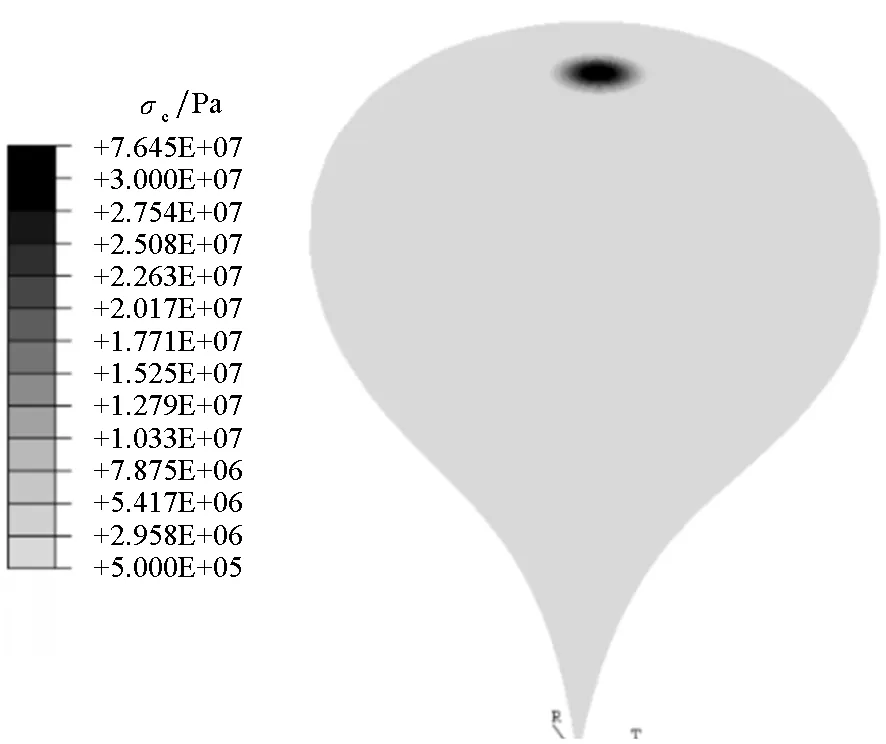
图11 周向应力分布云图(30 km)Fig.11 Circumferential stress distribution cloud chart(30 km)

3 关键参数敏感性分析

在球形设计的基础上，选取在高空气球设计时最重要的若干个关键参数，即飞行高度、载荷质量及昼夜温差，研究了这几个量在变化时对气球形状的影响。

3.1 高度变化的影响分析

对气球在携带相同质量载荷(1000 kg) 的情况下，进行了不同飞行高度(10 km,15 km,20 km,25 km,30 km,35 km,40 km)球形的计算，结果如图12～13所示。

由图可以得出，随着高度的增加，气球体积增加逐渐加快，而球体高度、截面圆半径和母线长度增加相对平缓。并且截面圆半径比球体高度增加稍慢，气球形状有向圆柱形发展的趋势。

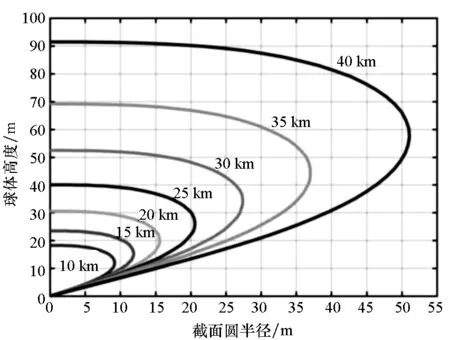
图12 相同载荷不同高度球形对比Fig.12 Shape contrast at different height under the same load

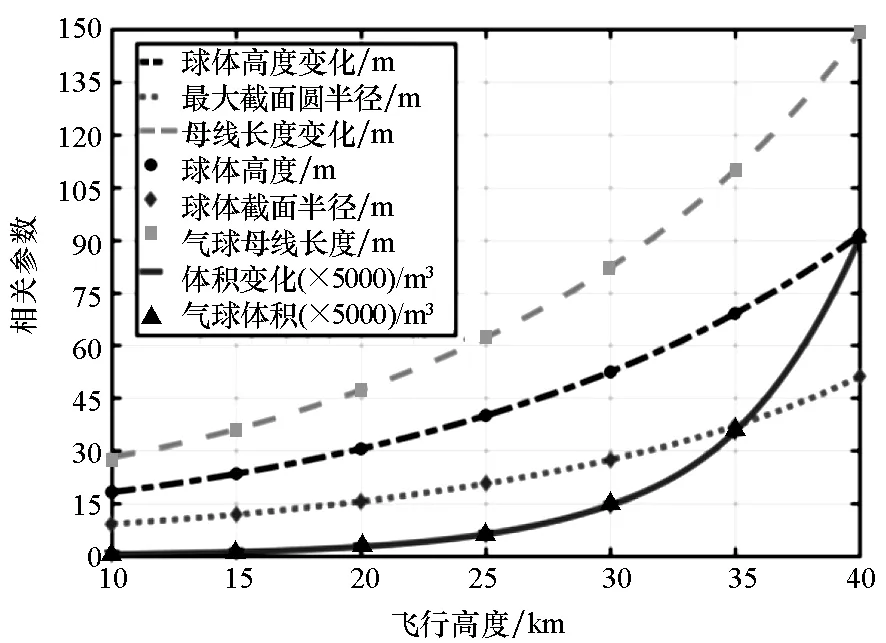
图13 相同载荷不同高度球形参数对比Fig.13 Comparison of shape parameters at different height under the same load

3.2 载荷变化的影响分析

对气球在相同飞行高度(36 km)、携带不同质量载荷(50 kg,100 kg,200 kg,400 kg,600 kg,800 kg,1000 kg)时的球形进行计算，结果如图14～15所示。

由图可以得出，在同一飞行高度下，随着载荷的增加，气球体积几乎保持线性增加，对比图8的结果，说明高度(压强)是影响气球体积大小的主要原因。球体高度、截面圆半径和母线长度增加逐渐平缓，有线性增加的趋势，这说明气球载荷对同一飞行高度气球的影响基本呈线性关系，符合以往的设计经验。

图14 相同高度不同载荷球形对比Fig.14 Shape contrast of different load under the same height

图15 相同高度不同载荷球形参数对比Fig.15 Comparison of shape parameters at different load under the same height

3.3 昼夜温差的影响分析

另外，零压气球底部有排气管与外界大气相通，使得底部压强差为零。在昼夜温差影响下，球内氦气温度发生变化，导致气球体积变化而引起气球飞行高度改变[12]。设计参数为飞行高度20 km，载荷质量1000 kg，膜密度20 g/m2的零压气球在北纬30°，春分时期，高度20 km处24 h内氦气温度变化引起的气球飞行高度、体积、球体高度及零压点高度变化曲线如图16所示。

可以得出，氦气昼夜温度有50 K的变化，引起气球体积在夜间缩小2500 m3，飞行高度偏离设计高度(20 km)达1.2 km，球体高度从30.5 m增高至32.75 m，零压点高度则有近10 m的变化。因此需要进行高度控制，工程上常采用投掷压舱物以减轻负载质量的手段[1]。超压气球则是利用超压量大于温度差引起的压强变化，使气球昼夜始终完全膨胀，能够在稳定高度飞行较长时间。

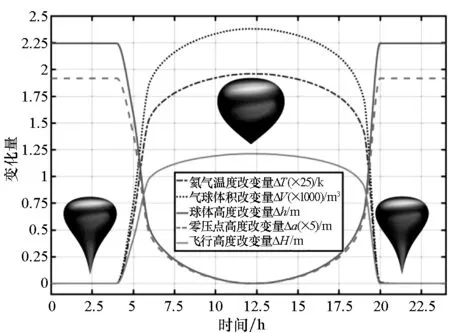
图16 昼夜温差引起零压气球参数变化Fig.16 Variation of zero pressure balloon parameters caused by temperature difference

4 总结

本文对零压式高空气球球形设计进行了系统分析，包括理论推导，设计数值方法进行求解，编写整套气球球体设计程序，以及对影响气球形状的关键参数进行敏感性分析及应用。首先借助薄膜无矩理论推导了气球球形的控制方程组，选择打靶法求解完全膨胀状态球形，并将多段打靶法与等式二次规划法相结合求解上升过程中的气球外形。随后，结合工程实际进行了算例分析：一方面与以往工程计算及文献结果进行了对比；另一方面结合有限元分析方法对计算得到的球形进行仿真，气球外形变化、受力平衡及应力分布情况表明球形符合零压气球应力假设，验证了设计方法的正确性。最后，对影响气球球形的飞行高度、携带载荷以及昼夜温差这些关键参数进行了灵敏度分析，给出了定量的计算结果，获得了有参考性的结论。总的来说，本文在之前学者的基础上对其方法做了进一步优化与改进，能够为后续研究人员提供相应的参考和借鉴。