不同分布式螺旋桨转向组合下的机翼滑流效应研究

, , ,*, ,

(1. 中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000;2. 中航工业第一飞机设计研究院, 陕西 西安 710089)

0 引 言

目前，航空喷气式发动机仍为运输类飞行器的主要动力且仍在不断进步，但关于未来航空运输的分布式螺旋桨推进、分布式涵道推进等各类电推进概念研究[1-3]早已开始，并将成为未来运输类航空飞行器的核心竞争力。美欧等航空大国早已投入巨资进行电推进相关的地面测试和飞行试验工作[4-8]，如LEAPTech[9-10]、X-57[11]、GL-10[12]、Lightning Strike、ECO-150[13]、STARC-ABL等。

一般来讲，分布式推进的主要设计优势在于提高气动效率和解耦动力能源，如机翼前缘安装分布式高升力螺旋桨的X-57能将起降状态升力系数提高到5.0以上，而在机翼和尾翼均安装若干螺旋桨的GL-10能实现垂直起降等控制策略。

关于分布式螺旋桨推进技术的气动分析，国内外相关研究较少。Stoll等[6]通过作用盘模型模拟分布式螺旋桨，对LEAPTech验证机进行着落状态定常滑流数值模拟，得到最大升力系数达到5.2，即达到同样的升力状态，分布式推进飞行器的机翼面积可以缩小到常规飞行器的三分之一。Patterson等[14]对采用翼尖和高升力两种螺旋桨的X-57“麦克斯韦”验证机进行分布式小直径螺旋桨设计分析，并对高升力螺旋桨(High-Lift Propeller，HLP)在低速状态下的潜在优势和挑战进行研究探讨，该高升力螺旋桨能在低速起降状态下高效运转，同时在高速巡航状态下桨叶能折叠且与短舱贴合，减小巡航阻力。Litherland等[15]基于X-57分布式螺旋桨推进方案，对高升力和翼尖螺旋桨电机和短舱散热进行分析。Dubois等[16]基于有限元方法对电动机和散热系统进行设计和优化，同时采用流热耦合数值模拟方法对电动机空气散热情况进行分析。

在螺旋桨滑流数值模拟方面，一般多采用基于作用盘方法的定常求解[17-20]和基于滑移/嵌套方法的准定常/非定常求解[21-26]。如李博等[17]采用等效盘方法对某四发涡桨飞机进行滑流影响研究；夏贞锋等[19]采用激励盘方法得到的单独螺旋桨滑流速度分布，与非定常滑流时间平均结果相吻合；王伟等[21]采用MRF方法对某双发涡桨飞机进行滑流效应研究，特别是滑流对全机纵向力矩特性影响情况；许和勇等[23]采用基于非结构动态嵌套网格技术的非定常求解方法，对前拉式螺旋桨飞机进行滑流效应研究；龚小权等[26]基于各向异性非结构嵌套网格的非定常求解方法，完成双发涡桨飞机不同前进比下全机滑流效应分析。采用非定常求解方法能获得更为真实的流动细节以及非定常滑流效应，而采用作用盘的定常求解更为简便，适合前期工程设计评估。考虑到分布式螺旋桨推进中桨叶数量多，非定常求解过程复杂且耗时更长，因此文中采用基于作用盘/等效盘模型的定常方法进行计算求解。

本文基于自主研发的“亚跨超CFD软件平台”(TRIP3.0)[27-28]，通过将等效盘模型替代分布式螺旋桨，完成四种分布式螺旋桨旋转组合下的机翼滑流效应研究，同时对单个螺旋桨正反转情况下的滑流效应进行分析，特别是单个螺旋桨滑流对机翼升阻力增量影响情况。

1 计算方法

1.1 控制方程

假设采用惯性笛卡儿坐标系，忽略彻体力，则Euler/Navier-Stokes方程可表达为：

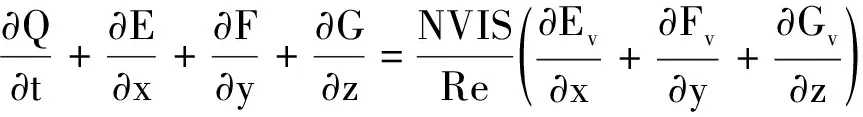
(1)

式中：

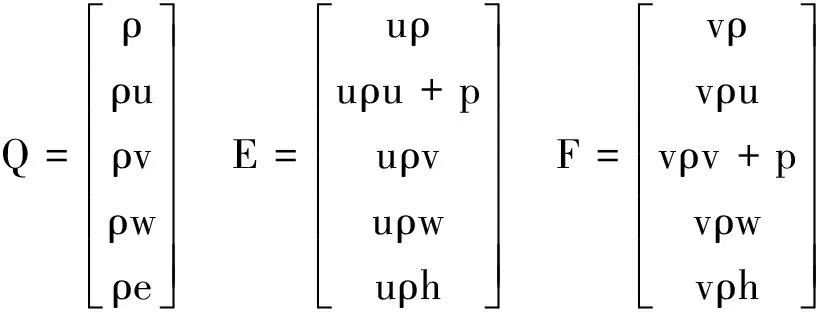
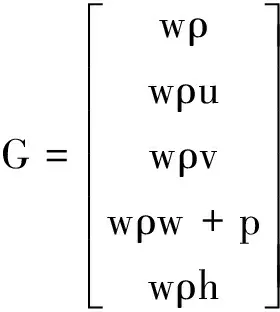
其中当NVIS=0时，方程求解为Euler求解；当NVIS=1时，则方程求解为N-S求解，式中ρ、u、v、w、p、e和h分别表示气体密度、x、y、z方向的绝对速度分量、压力以及单位质量的总能和总焓。

1.2 等效盘模型

为此采用基于动量-叶素理论的无厚度圆盘代替分布螺旋桨，模拟桨叶对气流的加速加旋效果，获得近似真实分布式螺旋桨的滑流影响，进而得到不同分布式螺旋桨转向组合下的机翼升阻力变化情况，其原理如图1所示，且不同迎角和侧滑角的盘前来流均能通过盘面坐标转换进行模拟。具体方法可参考文献[17]和[20]。

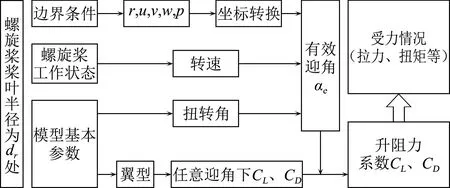
图1 等效盘模型原理示意图[20]Fig.1 Schematic diagram of the actuator model method

2 算例验证

算例主要参考单桨风洞试验结果，验证等效盘方法计算的拉力扭矩特性，同时采用非定常计算得到的滑流速度分布，验证等效盘方法计算的滑流效应。关于该计算平台的机翼算例验证可参考文献[27]等研究工作。

2.1 研究对象

研究对象为某螺旋桨试验外形，该螺旋桨为六叶桨，直径约为0.5 m，为避免弹性变形对结果影响，桨叶采用复合材料提高刚度。风洞试验在法宇航F1增压风洞完成，试验风速为50～79 m/s，前进比范围为0.92～1.48，如图2所示。

图2 螺旋桨风洞试验图Fig.2 Wind tunnel tests for propeller

2.2 计算网格及方法

定常计算网格为全对接结构网格，桨毂前段真实螺旋桨采用无厚度圆盘替代，O型结构拓扑，全模网格量约76万，图3给出了螺旋桨定常网格示意图。

图3 螺旋桨定常网格示意图Fig.3 Steady grid of single propeller

非定常计算采用动态拼接网格技术，网格量为1400万，其中旋转域网格量950万，静止域450万，总网格块数402块。图4给出螺旋桨非定常网格示意图。

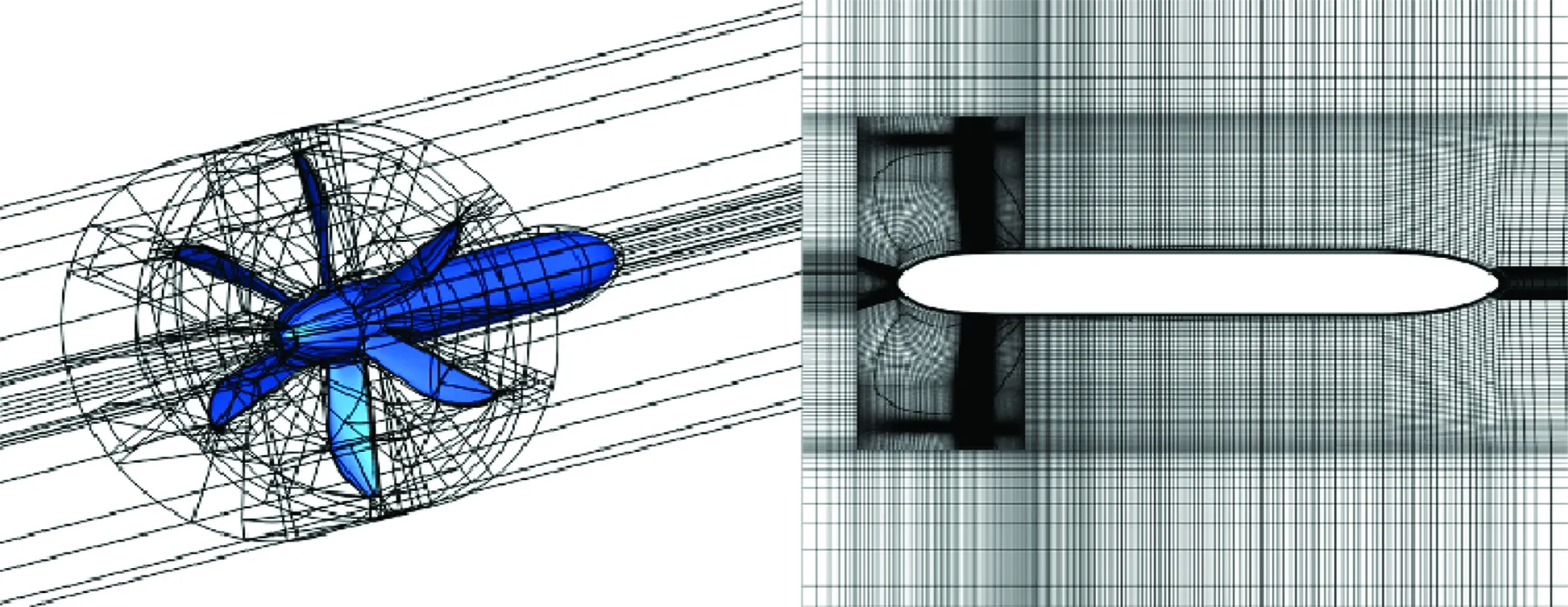
图4 螺旋桨非定常网格示意图Fig.4 Unsteady grid of single propeller

计算均采用雷诺平均N-S方程，SA湍流模型，定常计算螺旋桨采用等效盘进行模拟。非定常计算基于动态拼接网格方法[24]，每个子迭代网格旋转3°。

2.3 拉力扭矩特性

选取两个试验工况作为定常计算状态，具体如表1所示。

表1 螺旋桨计算工况参数Table 1 The condition of propeller for calculation

表2给出了单独螺旋桨定常计算结果与试验值对比情况。可以看出：计算得到的拉力和扭矩系数与试验值吻合较好；在小拉力状态，计算得到的扭矩系数与试验值吻合更好；在较大拉力系数下，拉力系数与试验值吻合更好。

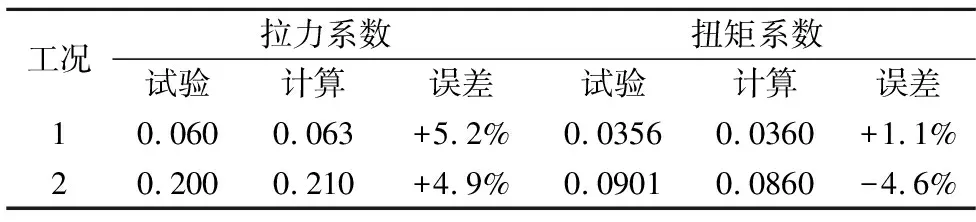
表2 螺旋桨定常计算与试验结果对比Table 2 The results of test and steady CFD

2.4 滑流速度分布

选取状态2作为分析对象，分别采用定常和非定常两种计算方法。表3给出两种计算方法与试验对比结果，非定常计算得到的拉力和扭矩系数与试验值吻合较好。

为了分析螺旋桨对气流的加速效应，图5分别给出定常和非定常时间平均(旋转一圈的流场结果平均)下桨叶后方0.6R处马赫数云图。定常计算得到的螺旋桨后方马赫数分布，与非定常时间平均的结果相吻合。

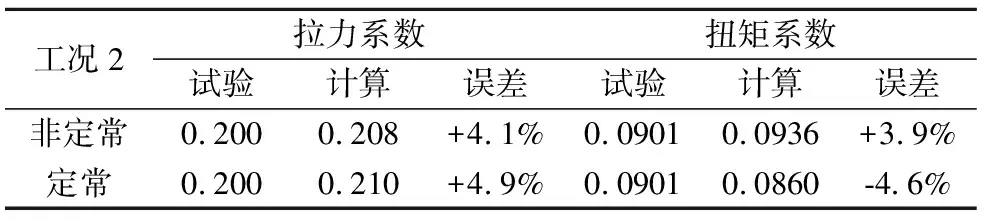
表3 螺旋桨计算与试验结果对比Table 3 Thecomparison between test and CFD results

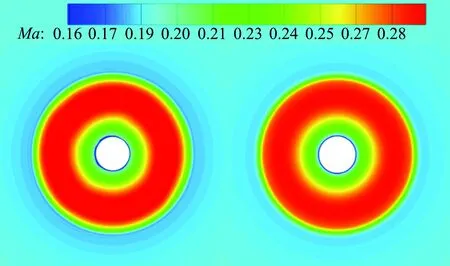
(a) steady (b) unsteady

图5桨叶后方0.6R处马赫数云图
Fig.5Machnumberat0.6Rrearofpropeller

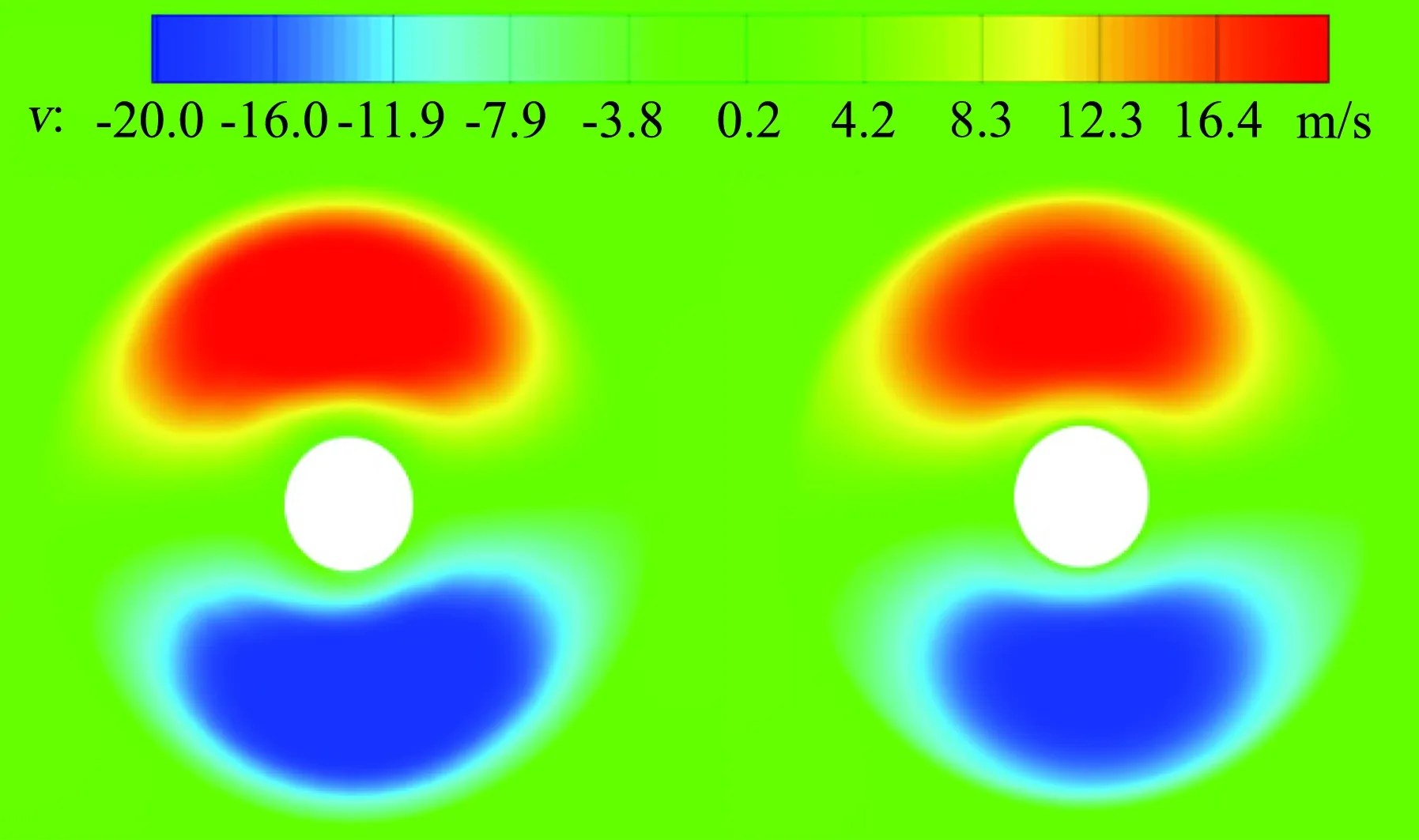
为了分析螺旋桨对气流的加旋效应，图6和图7分别给出定常和非定常时间平均(旋转一圈的流场结果平均)下桨叶后方0.6R处横向和纵向速度云图。定常计算得到的螺旋桨后方横向和纵向速度分布，与非定常时间平均的结果基本吻合，仅在加速区域上略微偏大，这主要是因为定常计算不能模拟桨叶三维分离等因素引起。因此，螺旋桨对气流加速加旋的滑流效应，采用等效盘模型能较好地进行模拟，且与非定常时间平均结果相近。图8给出了两种方法得到的空间流场示意图。

(a) steady (b) unsteady

图6桨叶后方0.6R处v方向速度云图
Fig.6Thev-velocityat0.6Rrearofpropeller

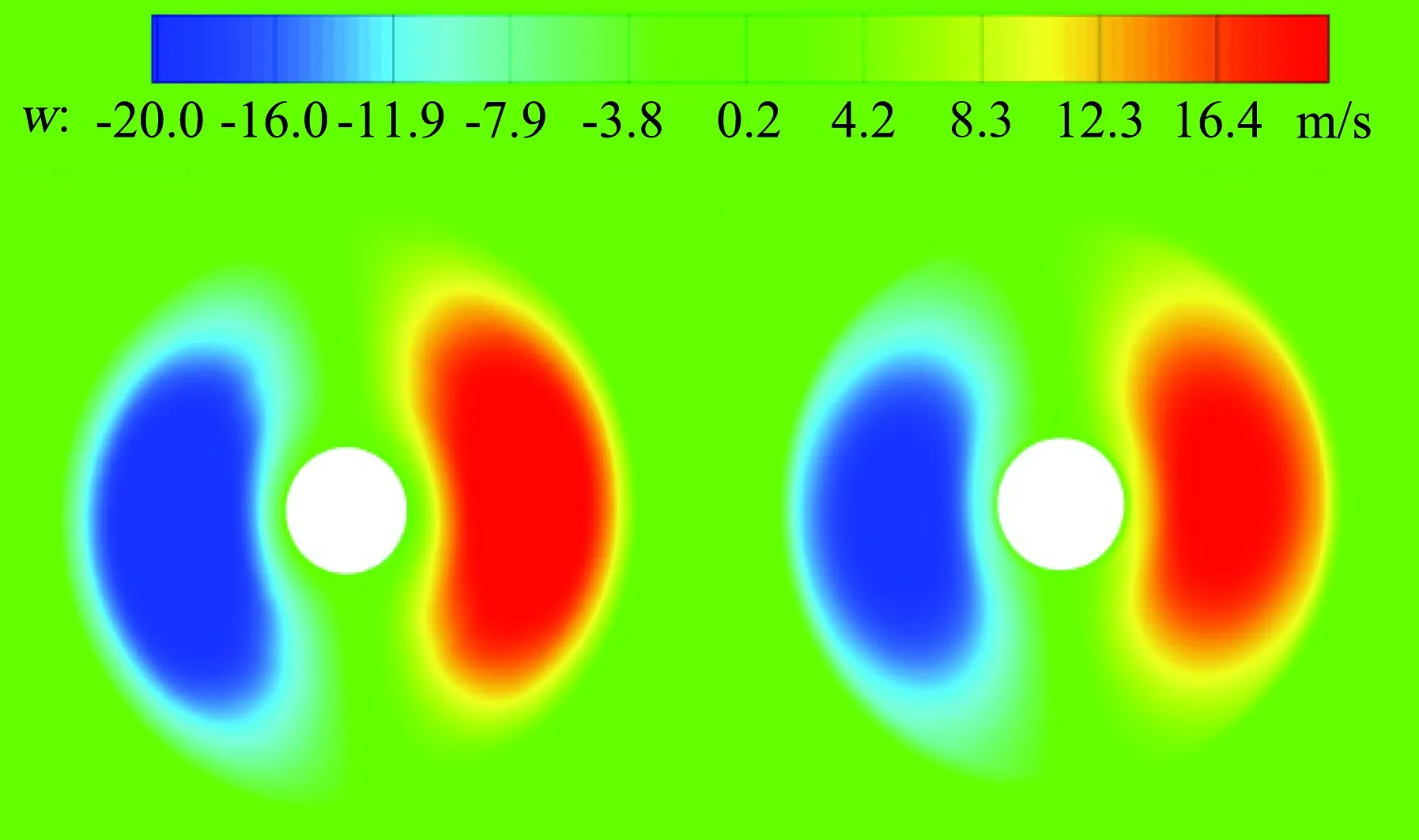
(a) steady (b) unsteady

图7桨叶后方0.6R处w方向速度云图
Fig.7Thew-velocityat0.6Rrearofpropeller

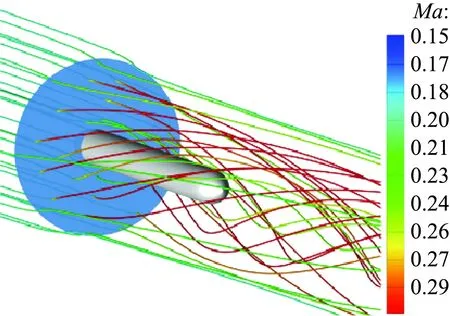
(a) steady

3 计算对象及网格

重点对前缘布置5个分布式螺旋桨的机翼进行不同转向组合下的滑流效应研究。

3.1 计算对象

该外形机翼前缘布置5个螺旋桨(如图9)，机翼翼展25.8 m，机翼面积为55 m2。图10给出了螺旋桨编号以及不同分布式螺旋桨旋转方向组合定义，其中螺旋桨桨叶直径均为2.4 m，单个螺旋桨包含三片桨叶。为后续方便进行滑流效应分析，定义顺流方向看，螺旋桨顺时针旋转(逆翼尖涡)为正。

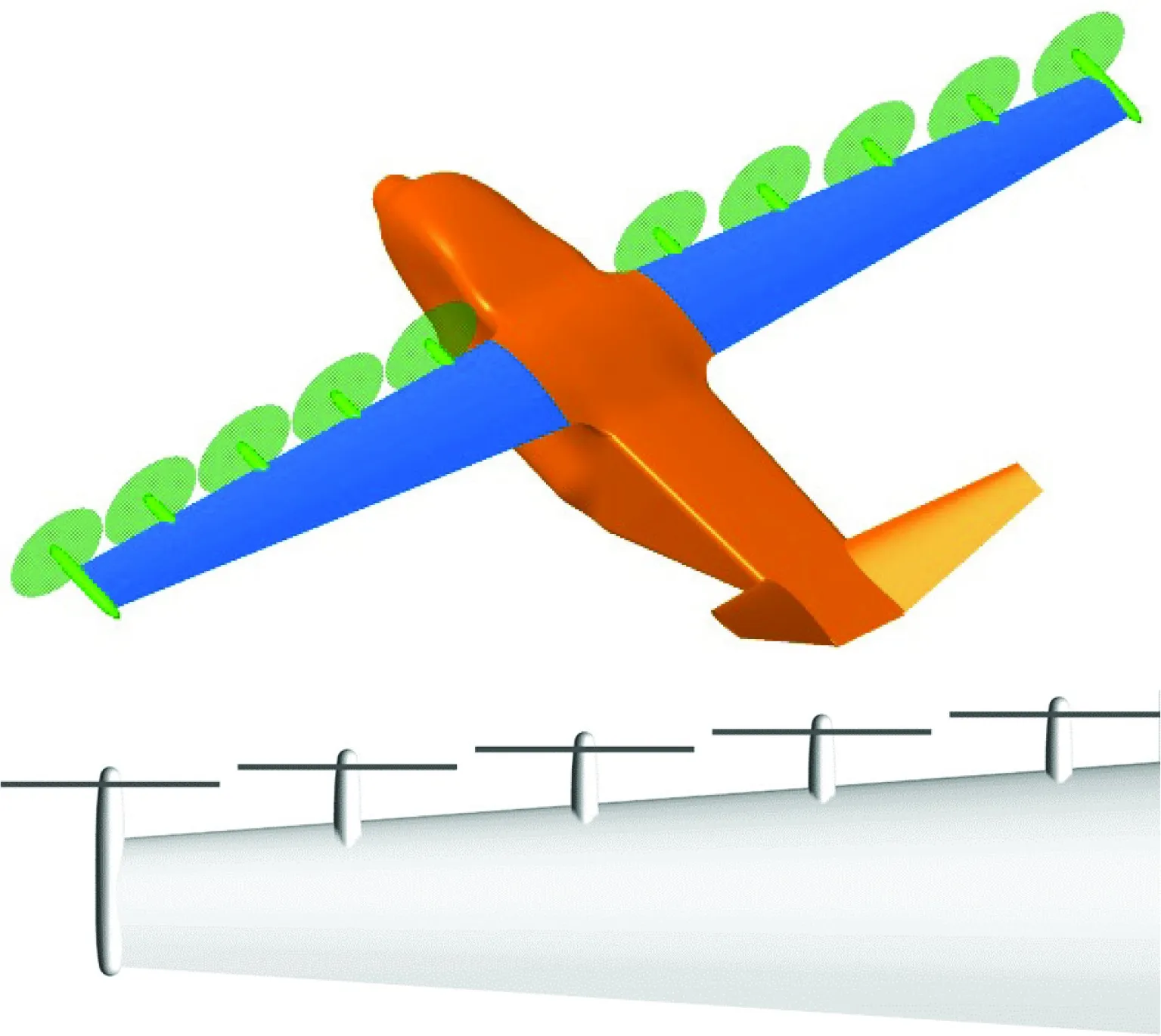
图9 分布式螺旋桨推进全机及机翼外形示意图Fig.9 Shape of a distributed propellers transport aircraft and the wing

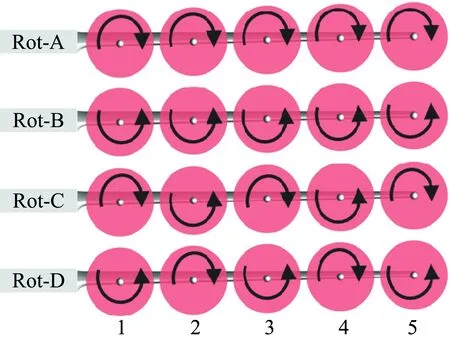
图10 分布式螺旋桨旋转组合方案Fig.10 The rotating direction of distributed propellers

3.2 计算网格

计算采用半模外形，网格为全对接结构网格，网格量约为2000万，网格块数260个，其中第一层网格距离约1.0×10-5m。网格在关键流场区域进行适当加密，特别是螺旋桨后方。机翼弦向和展向网格布点数为70×120个。螺旋桨采用无厚度圆盘代替，具体网格示意图如图11和图12所示。

图11 机翼及螺旋桨盘面表面网格Fig.11 Mesh on the transport aircraft surface

图12 翼尖部分网格示意图Fig.12 Mesh near the wing and propellers

3.3 计算方法及状态

采用雷诺平均N-S方程，离散方程组求解应用LU-SGS方法，空间方向粘性项采用二阶中心格式离散，无粘项为MUSCL-Roe格式，SA湍流模型，为加快计算收敛速度，采用低速预处理技术、大规模并行计算和多重网格技术。

以起降状态作为分析工况，来流速度200 km/h，迎角范围为-2°～14°，分别考虑有无滑流情况。有滑流状态螺旋桨速均为1550 rpm，桨叶半径70%处桨距为28.0°。为更好地分析不同螺旋桨旋转组合，分别对Rot-A、Rot-B、Rot-C和Rot-D四种组合方案(如图10)进行滑流效应研究，同时分别完成单个螺旋桨正反转滑流影响分析。

4 不同旋转组合方案分析

主要分析不同分布式螺旋桨旋转组合方案下的机翼滑流效应，分别机翼气动特性、压力分布及典型流场三个方面开展分析说明。

4.1 机翼气动特性

图13给出了四种不同分布式螺旋桨转向组合下的机翼阻力、升力、俯仰力矩系数以及升阻力极曲线。在阻力系数上，小迎角下Rot-B阻力最大，Rot-A和Rot-C相对更小；在升力系数上，小迎角下四种方案相差较小，且Rot-A相对其他方案略大；Rot-B在较大迎角下升力系数仍能保持较好线性度；在俯仰力矩系数上，Rot-B低头力矩相对其他方案偏大；在升阻力极曲线上，升力系数在0.24以内，Rot-C和Rot-D阻力更小，且在升力系数0.24以上，Rot-A和Rot-C较其他方案阻力更小。

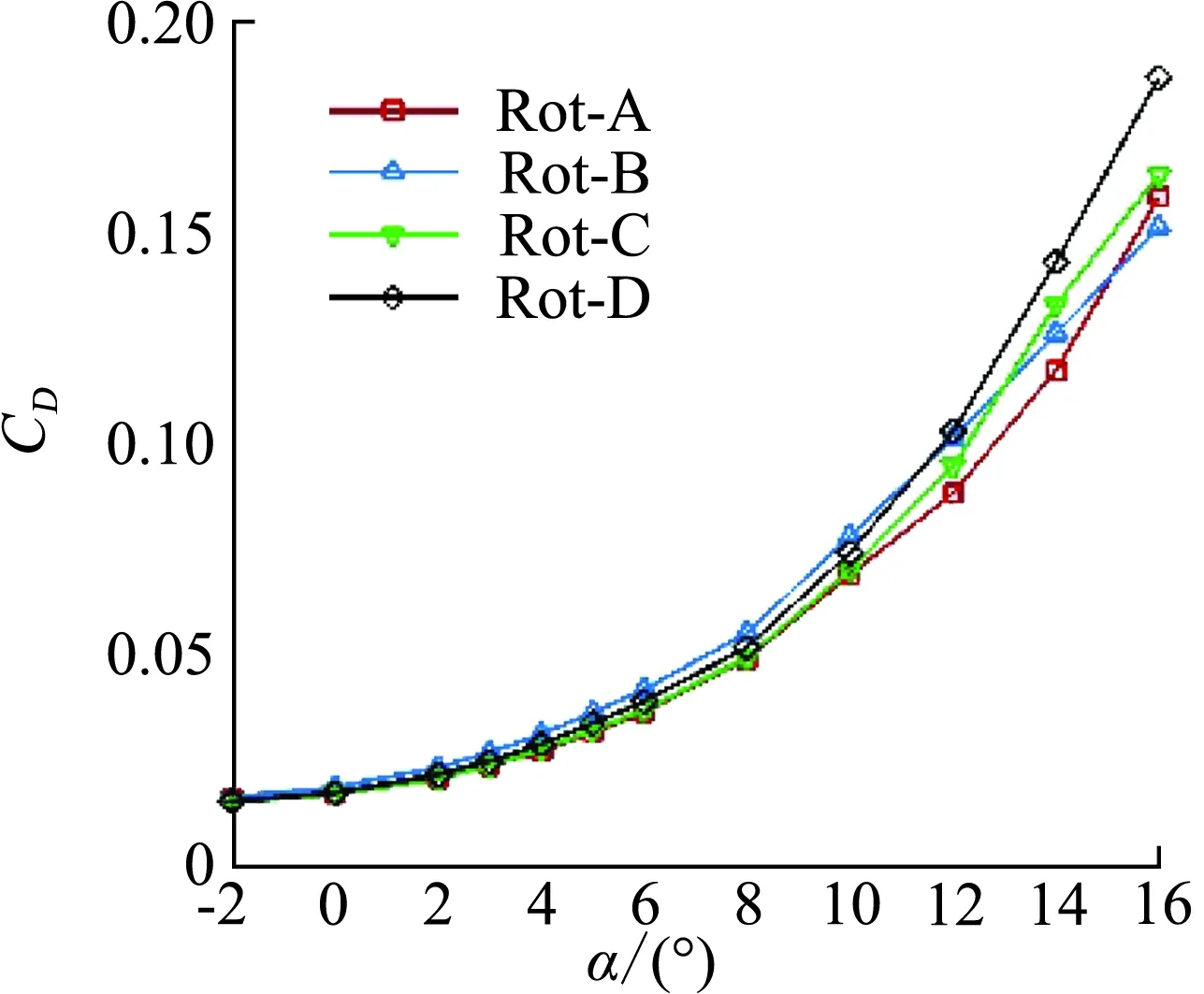
(a) CD～α

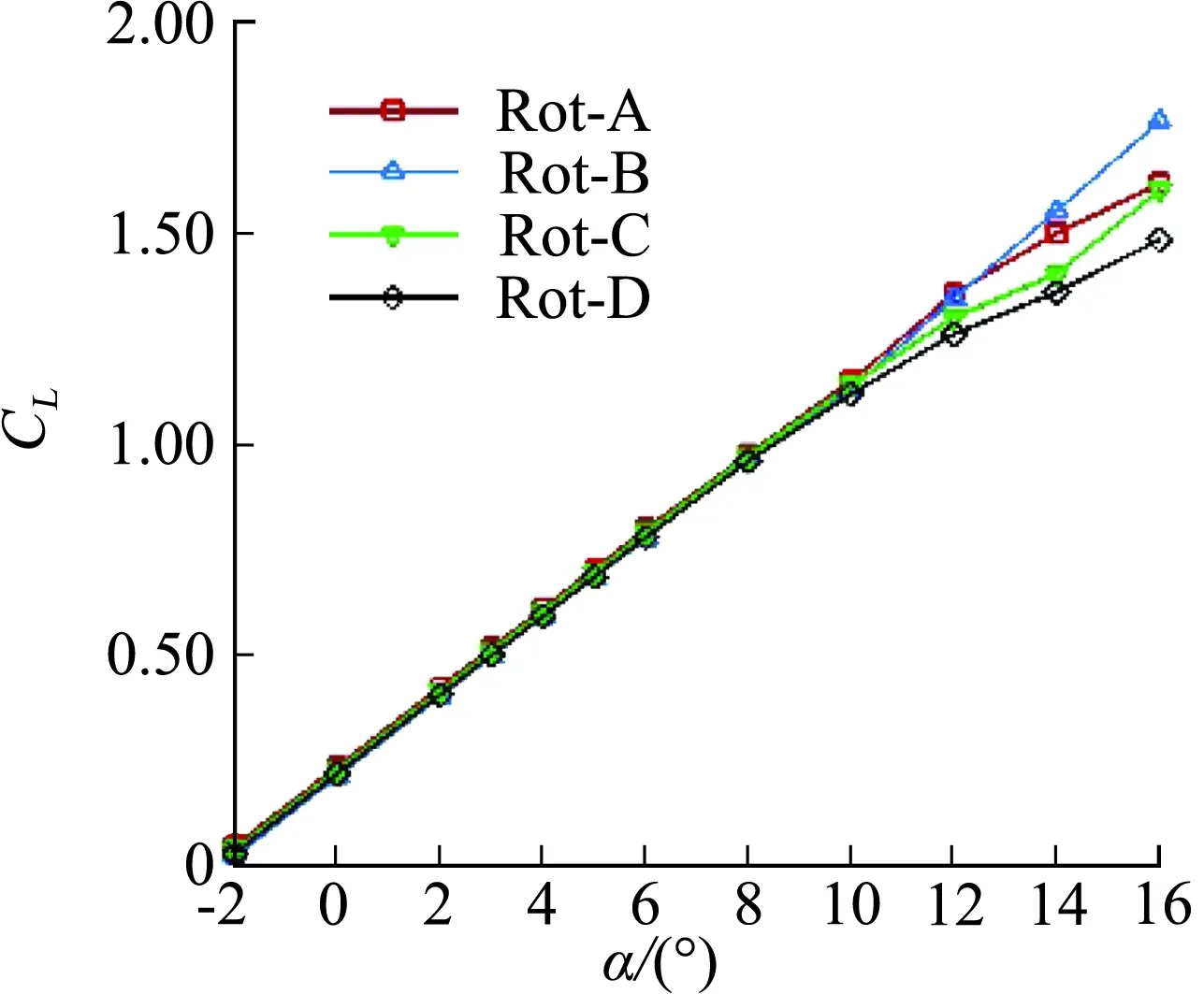
(b) CL～α

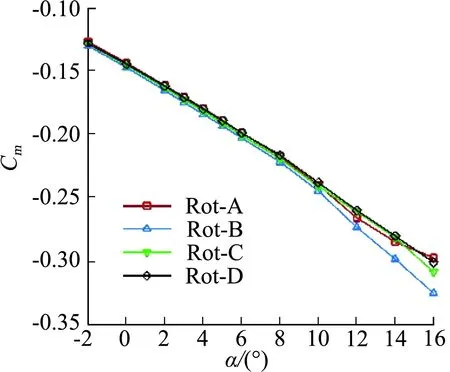
(c) Cm～α

(d) CD～CL

为进一步分析不同转向组合下的机翼升阻力特性，图14给出了有无滑流的四种螺旋桨转向组合下机翼升阻力系数增量，四种转向组合下的滑流均引起阻力和升力增大；在迎角α=8°以内，Rot-A和Rot-C阻力系数增量两者基本相同，且均小于另外两种方案；在较小迎角下，Rot-A升力系数增量最为显著，Rot-C次之。

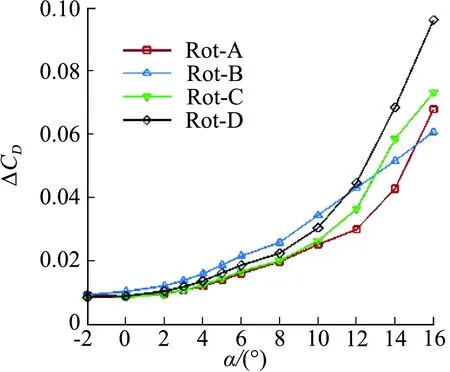
(a) ΔCD～α

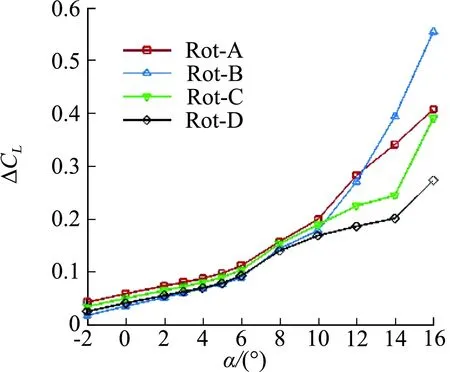
(b) ΔCL～α

以迎角α=3°为例，表4给出了不同螺旋桨转向组合下的有无滑流下机翼升阻力增量情况。此时，有滑流较无滑流状态机翼阻力均增加约81%以上，升力增加约14%以上；Rot-B阻力增加最大，而Rot-A升力增量最大；Rot-A和Rot-C阻力增量相同，均较另外两种方案小，且Rot-A的升力更大；Rot-B和Rot-D升力增量相近，但Rot-B阻力更大。同时，文献[6]中LEAPTech验证机采用Rot-C的分布式螺旋桨转向组合方案，这与机翼增升减阻存在一定关系。

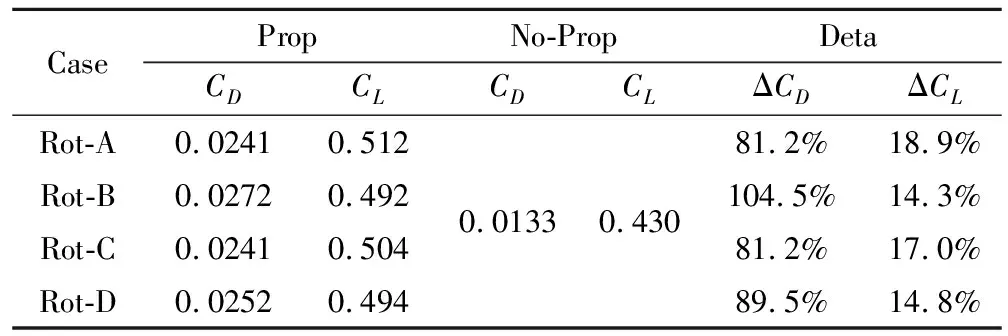
表4 不同组合方案在α=3°状态机翼升阻力增量Table 4 The difference of drag and lift of the four cases at α=3°

4.2 机翼压力分布

图15给出了迎角α=3°下，Rot-A和Rot-B两种转向组合机翼1/4弦长处压力分布，从上表面吸力峰数量看，Rot-A有5个明显吸力峰，而Rot-B存在4个；从下表面吸力峰数量看，Rot-A有4个较为明显吸力峰，而Rot-B存在5个。这主要是Rot-A方案翼尖螺旋桨逆翼尖涡旋转，在滑流作用下翼尖上表面存在较明显的吸力峰。

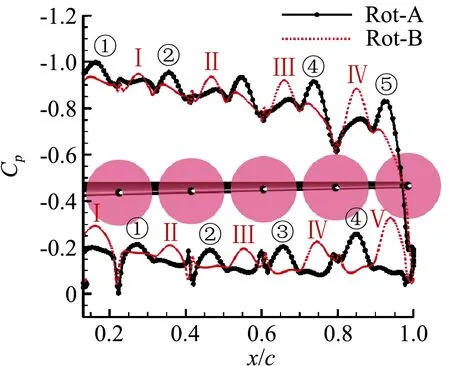
图15 两种转向组合下的机翼1/4弦长处压力系数分布Fig.15 Pressure coefficient distribution at 1/4 wing section with Rot-A and Rot-B

为方便分析机翼展向站位压力分布，图16为三个机翼站位示意图。图17给出了不同转向组合下的机翼站位±0.63R处压力分布，Rot-A和Rot-C方案在站位-0.63R前缘吸力较Rot-B和Rot-D大，而在站位+0.63R正好相反；在站位-0.63R处，Rot-A前缘吸力较Ror-C略小，而在站位+0.63R处，Rot-B前缘吸力较Ror-D略小，即对于相邻桨叶转向相反情况而言，其转轴中间区域机翼的前缘吸力相对转向同向状态有所加强。这主要是相邻桨叶转向相反，其转轴中间位置桨叶均处于上行或下行状态。

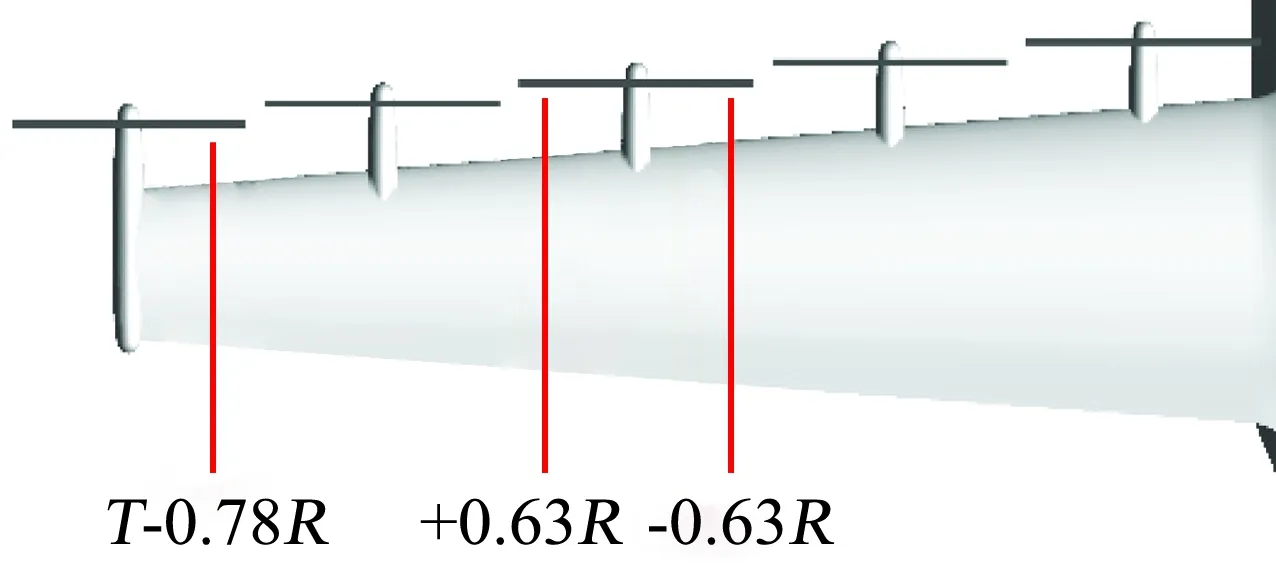
图16 机翼站位示意图Fig.16 The sections distribution of wing

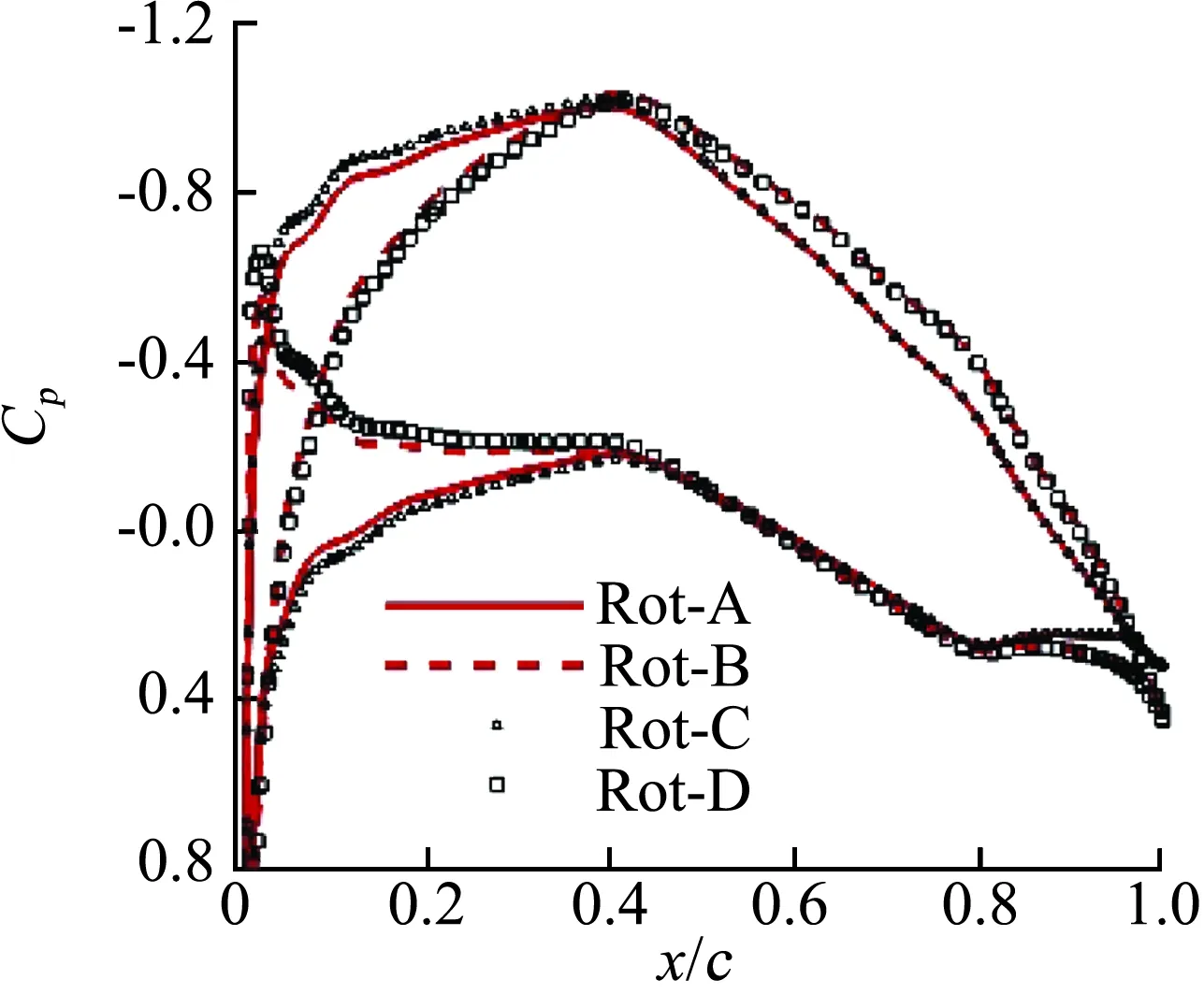
(a) Z=-0.63R

(b) Z=+0.63R

为进一步分析不同转向组合对机翼翼尖影响情况，图18给出了机翼翼尖附件站位T-0.78R处的压力系数分布。Rot-A和Rot-C方案前缘吸力较Rot-B和Rot-D明显偏大；Rot-C前缘吸力较Rot-A偏大，这与图17结论相同。同时由于该站位位于机翼翼尖螺旋桨滑流区域，翼尖螺旋桨转向对该区域的滑流影响对全机升力影响较大。

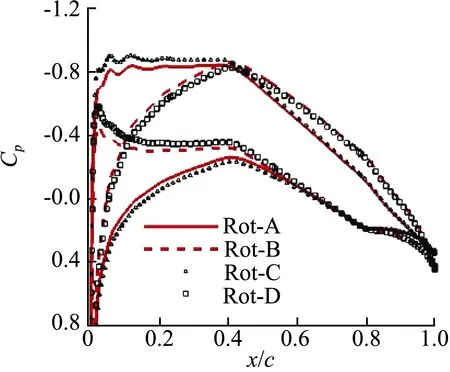
图18 不同转向组合下的机翼站位T-0.78R处压力系数分布Fig.18 Pressure coefficients distribution at T-0.78R sections of the four cases

4.3 典型流场

重点对迎角α=3°下，机翼上下表面压力云图和螺旋桨附近站位流线进行分析，特别是机翼上下表面压力峰值。图19和图20分别给出了不同转向组合下的机翼上表面和下表面压力云图。从上表面压力云图来看，Rot-A和Rot-C存在5个明显的前缘低压区，而Rot-B和Rot-D则为4个；从前缘低压区与螺旋桨轴线相对位置来看，Rot-A均位于右侧，Rot-B均位于左侧，这主要和螺旋桨转向密切相关；在翼尖部分，Rot-A和Rot-C低压区域较Rot-B和Rot-D明显偏大。从下表面压力云图来看，四种方案在机翼前缘差异明显，而在后缘差异较小；Rot-A和Rot-C存在5个明显的前缘高压区，而Rot-B和Rot-D则为4个。

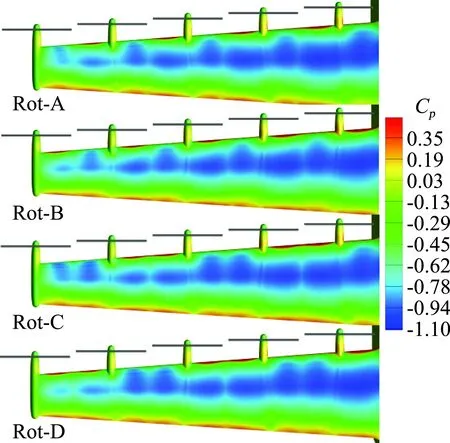
图19 不同转向组合下的机翼上表面压力云图Fig.19 Pressure coefficients distribution at upper surface of the four cases

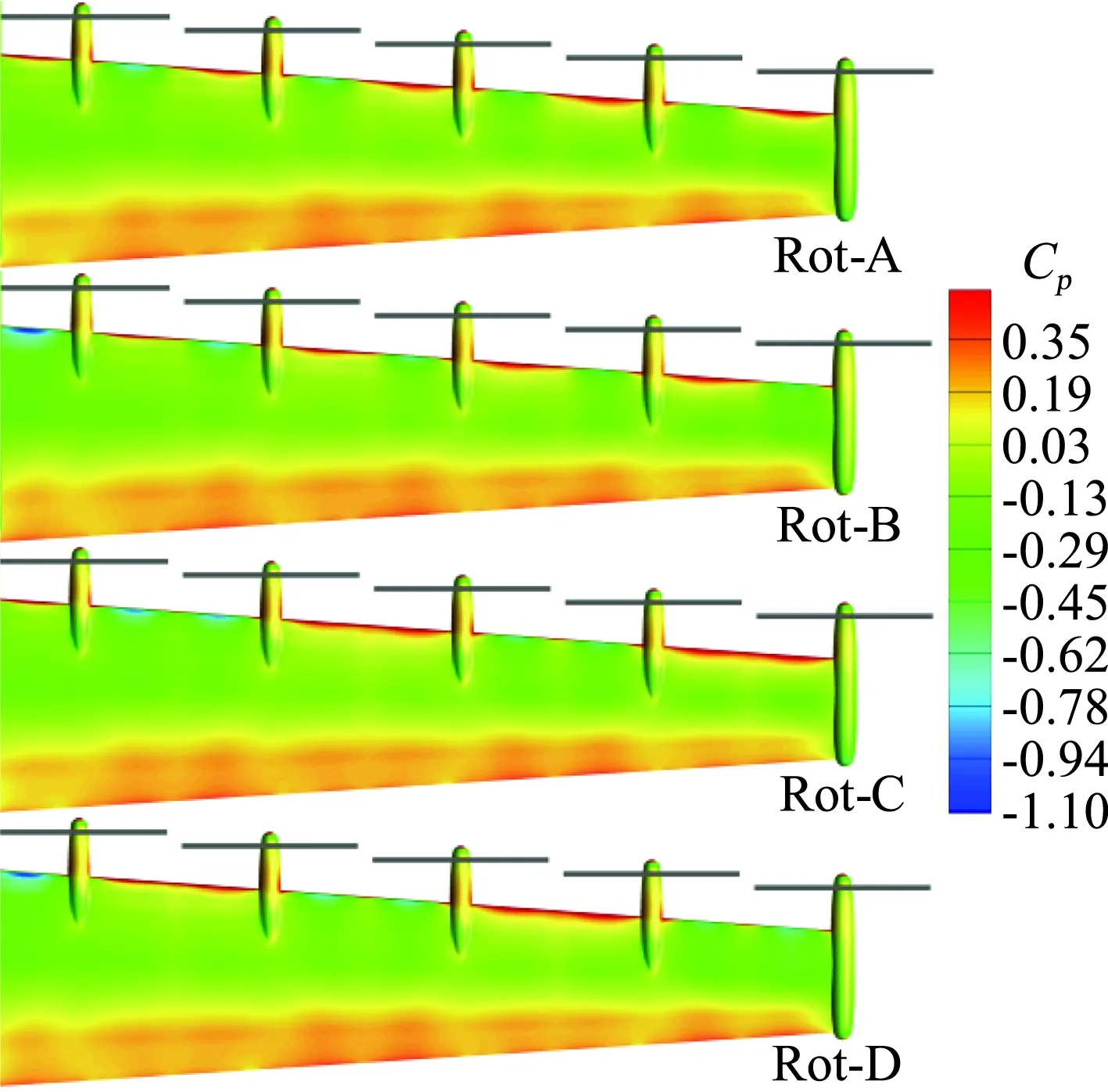
图20 不同转向组合下的机翼下表面压力云图Fig.20 Pressure coefficients distribution at lower surface of the four cases

图21给出不同转向组合下的机翼站位压力云图和流线示意图，其中在Z=-0.63R和Z=+0.63R两个站位处，Rot-A和Rot-C螺旋桨转向相同，Z=-0.63R处气流经过桨叶后均向上偏转，Z=+0.63R处气流经过桨叶后均向下偏转，且两者压力分布基本相近；Rot-B和Rot-D螺旋桨转向相同，Z=-0.63R处气流经过桨叶后均向下偏转，Z=+0.63R处气流经过桨叶后均向上偏转，且两者压力分布基本相近；在Z=-0.63R处，Rot-A翼型低压区较Rot-B更靠前，且低压区更大，而在Z=+0.63R处恰好相反。这主要是桨叶上行一侧机翼有效迎角增加，低压区前移且较大，桨叶下行一侧机翼有效迎角减小，低压区后移且较小。

(a) Z=-0.63R (b) Z=+0.63R

图22给出了迎角α=3°下，不同分布式螺旋桨转向方案下的有无滑流机翼1/4弦长马赫数差量云图。四种分布式螺旋桨旋转组合下，均在螺旋桨后方出现明显的滑流区，即气流被加速；Rot-A和Rot-B马赫数差量较大区域均在螺旋桨同侧，而Rot-C和Rot-D正好相反；除翼尖螺旋桨正转状态外，其余状态螺旋桨均存在明显的马赫数差量，且均位于机翼下方，这主要是桨盘在正迎角下，下行桨叶有效迎角增加，上行桨叶有效迎角减小，引起下行桨叶一侧滑流动压增量较上行桨叶一侧偏大。

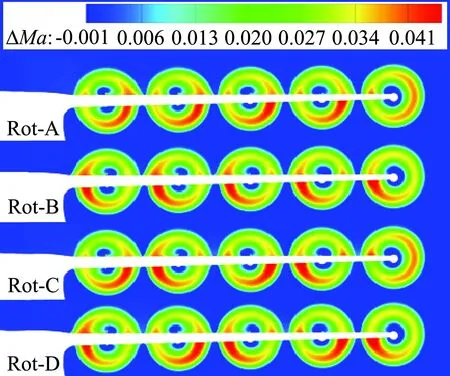
图22 有无滑流机翼1/4弦长马赫数差量云图Fig.22 Mach number difference at 1/4 wing section of the four cases

5 单个螺旋桨正反转分析

为了更好地分析该分布式螺旋桨布置方式对机翼滑流影响情况，分别对单个螺旋桨正反转情况下的滑流效应进行研究，特别是滑流对机翼升阻力增量影响情况。此时，每个螺旋桨转速均为1550RPM，桨叶半径70%处桨距均为28.0°。

图23分别给出单独螺旋桨正反转滑流状态下，迎角α=3°和α=5°机翼相对无滑流的升阻力增量情况。在两种迎角状态下，单独螺旋桨滑流对机翼升阻力影响基本相近；相对无滑流状态而言，除翼尖螺旋桨外，单独螺旋桨正反转滑流均引起阻力增加，升力增大；对于翼尖螺旋桨而言，螺旋桨正转(逆翼尖涡方向)阻力较无滑流状态更低，而升力反而增大，螺旋桨反转(顺翼尖涡方向)则效果正好相反，即翼尖螺旋桨逆翼尖涡方向旋转具有增升减阻效果；除靠近翼根螺旋桨外，其他单独螺旋桨正转状态下阻力较反转小，且越靠近翼尖越显著；除翼尖螺旋桨反转状态外，其他螺旋桨滑流状态对机翼升力增量大小相当。这主要是螺旋桨逆翼尖涡方向旋转，能极大削弱翼尖涡的强度，从而降低机翼诱导阻力。

(a) α=3°

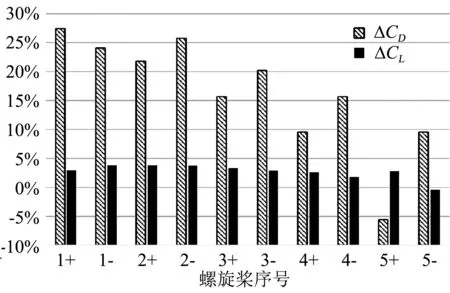
(b) α=5°

6 结 论

通过完成分布式螺旋桨的机翼不同转向组合下的滑流效应研究，并对单个螺旋桨正反转状态下机翼升阻力增量情况分析，得到如下结论：

1) Rot-A和Rot-C方案的升阻特性相对其他两种均更优，若考虑到Rot-A方案存在动力共振、反扭力矩平衡等问题，Rot-C方案则相对最优；

2) 四种转向组合下的滑流均引起阻力和升力增大，在迎角α=8°内，Rot-A升力系数增量最为显著，Rot-C次之，且Rot-A和Rot-C阻力系数增量两者基本相同，均小于另外两种方案；

3) 相邻桨叶转向相反时，其转轴中间位置桨叶均处于上行或下行状态，使得转轴中间区域机翼的前缘吸力相对转向同向状态有所加强；

4) 分布式螺旋桨机翼升力与滑流作用下机翼上下表面吸力峰数量关系密切，特别是翼尖螺旋桨旋转方向；

5) 翼尖螺旋桨逆翼尖涡方向旋转，能极大削弱翼尖涡的强度，具有增升减阻效果；

6) 通过分析发现该方案得到的分布式滑流对机翼增升效果较为明显，但仍未能充分体现分布式螺旋桨推进的显著优势，这可能与机翼展弦比、螺旋桨数量及布置方式等有关。因此下一步将继续探讨分布式滑流对机翼气动特性影响情况，充分发掘分布式螺旋桨推进的潜在优势。

致谢:在此对课题组张玉伦、洪俊武、王光学、张书俊、孙岩、李伟、王昊、岳皓表示感谢。