面向精准工程湍流模型的理论研究

, ,

(湍流与复杂系统国家重点实验室, 北京大学 工学院, 北京 100871)

0 引 言

理论空气动力学研究的一个“卡脖子”问题在于对湍流边界层的精确描述，具体反映在计算流体动力学(Computational Fuid Dynamics, CFD)中的湍流模型发展瓶颈上。高速发展的航空航天工程，对CFD的计算精度、计算速度以及可计算工况的广度不断提出更高的要求。然而，传统工程湍流模型建构在量纲分析方法的基础上，所引入的经验参数(甚至经验函数)数量众多，不具有普适性，每一次的修正都会引进新的参数，而且都是依托风洞实验的宏观测量来进行(后续)校正，缺乏对于流动的物理机理分析。所以，对于工程湍流的预测依然停留在类似于中世纪对行星轨道描述的托勒密阶段。因此，尽管近年来实验和计算的数据猛增，并没有带来对边界层预测质量的大幅度提高。背后的深刻原因是缺乏一个对描述湍流边界层的完整理论。这也使得工程湍流模型的适用范围始终是未知的，参数随空间和流动外界条件的变化规律也是未知的。对于实际应用而言，这导致了二个后果：一是计算精度有限，例如翼型阻力预测的精度一直存在着无法修正的几十个Counts的偏差(一个Count是10-4)，二是随流动物理条件改变时，参数的变化规律未知，需要工程师的人为“艺术化”干预。因此，对于复杂流动，尤其是涉及多种流态的流动，CFD计算的绝对精度是不确定的，甚至难以完成计算任务。一旦面对高超声速、临近空间等超常物理环境、实验无法模拟的情况时，计算预测的不确定度就构成了真正的“卡脖子”问题[1]。

空气动力学研究自身还存在一个状况，就是基础研究远远落后于工程模型研究的需要。关于规范壁湍流的基本理论，即近一个世纪前的Prandtl-von-Karman的对数律理论，是不完整的，它只刻画了一小部分流域(即所谓的对数区)。而非对数区的流动描述长期依赖于经验。对于风洞实验和计算机模拟过的规范壁湍流，人们对非对数区已经形成了丰富的经验知识，也拥有全流域的经验模型，能够对平均速度剖面进行刻画(但对于动能剖面还不能进行有效刻画)。工程需求使人们只关注哪些预测能力还比较差的流动(例如包含激波和分离的流动)，或者是物理因素未知的系统(例如，分子热运动的涨落效应明显的稀薄气体，以及化学反应出现跨尺度耦合的燃烧等)。这就产生了一个错觉，认为对于基本的规范壁湍流(如槽道圆管等)已经都清楚了。其实，对数律理论在描述域上的不完整同时意味着理论框架的不完整，以及对边界层物理描述的不完整，这一不完整正是其无法向各类非规范壁湍流(即实际工程流动)进行应用的原因。为了使湍流模型的研究出现突破(而不总是修修补补)，必须从根本上解决一些重大问题。著名的湍流世纪难题，即完成对平板边界层的速度和动能剖面的完整预测，就具有十分重大的意义。

于是，本文围绕着如何利用近几十年来高精度计算和实验所积累的流动脉动的资料，在湍流研究的基本概念上寻求本质性的创新展开讨论。我们认为，过去几十年湍流基础研究进入了一个瓶颈，是因为研究思路的局限，没有真正认识壁湍流的普适性原理[2]。本文所介绍的结构系综理论寻求建立从简单的规范壁湍流到工程复杂湍流的一致性的研究框架，实现对壁湍流的基础认识上的突破，从而产生在物理图像和预测精度上远优于基于对数律理论的当代工程湍流模型，从而带来工程湍流预测精度和确定性的本质性的提高。

1 工程湍流模型研究的困难和出路

快速稳定的RANS(Reynalds Averaged Navier-Stokes)计算是解决工程湍流问题最有效的选择，工程上广泛应用的CFD模型，绝大部分基于RANS方程，其核心难题仍然是湍流模型。其问题主要在于，一方面缺乏对湍流普适性原理的理解；另一方面，人们希望的能够适用于各种流场的普适精确的湍流模型没有出现，而不同湍流模型之间的区别又难以把握，使得湍流模型对于其使用者的选择能力有很高的要求[3]。毫无疑问，创建适用于低速与高速、包含层流到湍流的转捩过程、有化学反应、有多种组分的复杂流动的精准湍流模型是空气动力学研究的核心难题。

CFD计算的一大难点是湍流边界层，这是因为其脉动和敏感特性，具体表现为转捩、激波、分离的位置的高度敏感，决定了飞行器的整体力学特性。另外，在发动机内部，还存在燃烧中化学反应与湍流的交互作用，多组分气体的输运行为预测[4]；更为复杂的问题出现在近空间飞行器再入大气层过程中，飞行器表面不同位置出现不同流态，甚至，连续介质力学方程的适用性都是问题[1]。近年来，快速发展的CFD技术在飞行器气动外形设计中起到越来越大的作用。气动优化设计方法中，流场的CFD计算量巨大。正是由于上述湍流模型的不确定性，CFD的气动优化设计还没有真正开展大规模应用[5]。以翼型计算为例，转捩问题就是一个突出的未解难题，它涉及到在流向由层流向湍流流态的转变，表现为速度、压力等物理量的大幅度变化，并进一步与激波、分离等复杂流动结构相互影响，使得精确预测翼型在各种工况下的力学性质(升阻力等)仍然是一个很大的挑战。

1.1 传统工程湍流模型研究的困难

常用的湍流模型包括BL(Baldwin-Lomax)代数模型(零方程模型)、SA (Spalart-Allmaras)一方程模型,k-ω和k-ε等二方程模型, 以及其他更加复杂的雷诺应力模型[6]。这些模型构造的数学基础主要是量纲分析，即对方程中(需要封闭)的高阶脉动量，从量纲分析上给出依赖平均量的函数形式，附加待定的(无量纲的)经验参数。虽然量纲分析是严格(普适)成立的，但无量纲参数的选取则与流动物理有关系，因此对于不同流动来说，经验的无量纲参数的数值就不再普适。换句话说，由量纲分析所给出的函数形式与边界层流动没有关联，使得湍流模型的物理内涵很肤浅[7]。过去，通过所预测的一些整体物理量(如升阻力)与实验值的比较来确定这些参数，是充满侥幸心理的，即希望这些参数是普适的。实践证明，这样所确定的参数难以给出精确的预测，为此，人们不得不一次次引进越来越复杂的函数变化(如k-ω模型方程里所包含的多个任意函数，或Menter的转捩模型中所包含的转捩函数)。这一切表明，关于湍流边界层的基本认识仍然停留在相对原始的层次上。

举例说，随着研究的深入，人们开始在k-ω方程中引进了对涡黏系数沿垂直方向附加的假设和新的系数，使得系数数目巨大。波音和空客公司拥有强大的风洞实验数据库(例如升阻力系数和压力分布系数等)，可以对这些参数进行校订，但是，这样的参数确定带有强烈的经验性(一些参数针对特定流动的取值是不公开的，属于商业机密)。

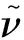
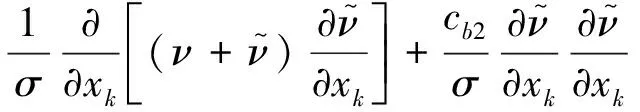
(1)

cω1=cb1/κ2+(1+cb1)/σ

(2)

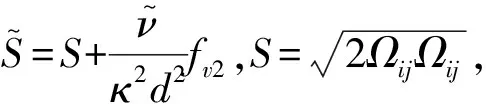
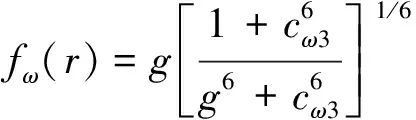
(3)

g=r+cω2(r6-r)

(4)

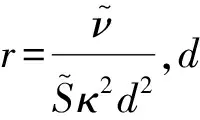
由于整个模型的构建过程依据的是直觉和量纲分析，模型参数与实际流动的物理几乎是完全没有联系的，这使得很难讨论模型参数如何随着流动物理条件的改变而变化。而湍流的一个重要特性就是力学性能随Re数、Ma数、固壁外形等物理条件的变化呈现非凡的相似律。缺乏与这些物理知识的联系，湍流力学特性不可能得到精确的预测。

1.2 工程湍流模型研究的系统性分析

湍流模型研究的创新一直以来受制于人们的一个认识，就是想拥有一个既普适、又精确的湍流模型，但这二点对于复杂湍流现象来说几乎是对立的。崇尚简单本质规律的物理学有这样一条公理，即一旦抓住了事物的本质，就一定会有一个简单而又精确的表达式出现。湍流研究的历史表明，不存在这样一个针对所有湍流系统的本质模型，即湍流是复杂系统。

让我们用系统论的思维来考察湍流模型的构建。由于多尺度脉动的激发，湍流运动存在内秉的复杂性，即存在从大尺度到小尺度连续激发的湍流脉动，它引出了湍流的非凡相似律。而不同湍流系统具有空间不同的变化形态，由此也会产生大小尺度之间稍许不同的相似规律，这就导致一旦以过于简单的量纲约束来描述的湍流平均运动规律会表现出差异。那么，是否存在相对于一类具有公共特性的湍流系统的普适物理原理呢？我们认为是一定的，只要该原理反映的是这一类湍流系统的公共特性。具体来说，针对壁湍流，固壁约束就是其公共特性，可能存在能够表述固壁的物理约束的原理，这就是本文后面要介绍的李群拉伸不变性原理。

“一元二面”的系统论[9]主张，如果抓住系统的一元，则对立的二面都得到掌控，此一元就是对于一类湍流(如壁湍流)的普适原理。对于一个复杂系统，存在多个对立的二面。首先，让我们来讨论内外二面，这对应于湍流系统的两大类复杂性，即来自流动内在的多自由度、多尺度性质，与来自于流动外部的多环境特征(如压力梯度效应、温度涨落效应等)，后者与湍流运动的开放性密切相关。让我们把目标锁定在具有公共外在特征的流动中，即最大限度地消除外在复杂性，这就是把壁湍流选为研究对象的原因[10]。注意到，过去相当长时间，湍流应用基础研究曾把研究对象锁定在均匀剪切湍流，这是有很大问题的。二者的差别是前者是真实流动，而且可以从简单的规范壁湍流(槽道，圆管，边界层)向机翼、折角、凸起等复杂外形延伸，后者是一个理想的人为设置，不能反映湍流的本质[2]，难以挖掘出真实壁湍流的普适规律(如后面要揭示的多层结构)。

另外一对二面是动静二面，湍流运动是非定常的，其脉动是其动的一面，而(时间平均的)剖面则是其静的一面。工程研究关心的是平均剖面的特性。近年来，随着实验和DNS技术的发展，精确的测量和数值模拟提供了大量的壁湍流的脉动场的信息。于是，人们的热情大量倾注在对于脉动场湍流结构的研究和刻画中。但针对湍流结构的基础研究与面向平均速度剖面的工程应用研究之间的壕沟始终存在，甚至出现一种日益扩大的地步。这正是湍流研究陷于困境的一个原因。

因此，重要的突破口应该是构建从第一性的基础性原理出发，又能直接服务于工程实践的湍流理论。20世纪30年代，Prandtl和von-Karman所提出的对数律理论[11,13-14]，正是有这样的影响力的理论，因此成为20世纪湍流理论研究的二大里程碑成果之一。这一理论的出发点是基于对称性的思考。假设固壁附近沿壁面的流动在近壁区和外区之间形成一个重叠区，这里湍流剪切(即速度梯度)与壁面距离所选择的单位无关，既可以用外区单位，也可以用内区单位。这时，平均速度剖面满足对数律。这个简单的对称性广泛存在于许多壁湍流当中，主宰了壁湍流的平均场运动，也成为脉动场的约束机制(自壁面产生的涡结构)，这是Prandtl-von-Karman长期能够指导工程实践的原因。

但对数律是一个局部近似解，在出现分离、激波等复杂流动时不再精确成立。因此，必须发现对数律背后的更加普适的原理，才能够构建一个可以描述复杂(现实)壁湍流的完整理论。这就是本文要讨论的约束湍流边界层的更广泛的对称性原理，从这样的原理出发可以构建更一般的复杂流动中精确的工程湍流模型。值得指出的是，这项基础性课题必须按照基础研究的方法来进行，即必须坚持从假设，到先验验证，再到针对复杂流动的预测和检验这样一个长期的努力，最终将能发展出一个与Blasius层流边界层理论相平行的完整的湍流边界层理论，即完全把握Re相似律的湍流边界层理论。这便是那个貌似简单、但一个世纪来未曾取得突破的湍流世纪难题[10]。

这项基础研究需要同时抓住简单与复杂二面背后的一元，为此，需要在研究方法上进行大幅创新。概括地说，当把研究对象聚焦在壁湍流时，必须提炼出能够反映固壁对流场产生(对称性)约束的相似变量。这样的相似变量是普适的，不仅仅适用于对数区，也适用于壁湍流的全流域，还适用于更加复杂的流动。这就是下一节要讨论的结构系综理论所发现的长度序函数的意义。于是，新理论既可以针对简单的规范壁湍流来完善Prandtl-von-Karman局部对数律的近似，又能够扩展去刻画更加复杂的研究对象(如压缩拐角，可压缩壁湍流，热对流，翼形流动等)，构成对真实湍流的刻画。

最后，针对工程湍流模型，人们已经意识到，CFD计算中的网格和计算格式，在空间上必须保证动量和能量平衡的某种守恒性[15-16]，而湍流模型则是针对(高阶)脉动结构所封闭产生的湍流耗散，它在时间维度上保证动量和能量平衡的实现。时间和空间也构成互补的二面，因此，网格和计算格式与湍流模型构成CFD完整计算的二面。上面提到的优良守恒性的格式[15-16]，也体现了对称性在CFD计算中的重要意义。与之对应，湍流模型的研究也更需要挖掘在壁湍流的脉动结构背后所主宰的对称性原理。只有揭示了这样的普适对称性原理，才能给出适用于复杂流动系统的高精度的工程湍流模型，满足工程需求[7]。

2 结构系综理论新探索

2.1 结构系综理论研究框架

在航空航天应用中，人们希望精确预测飞机的气动力与气动热特性(以实现增升、减阻、降噪和热防护的设计需要)，这就需要准确把握气动特性随飞行器表面外形以及Re数、Ma数的相似性规律。湍流模型的核心内涵应该就是把握这一相似性，因此湍流模型背后的理论应该是相似性理论。而传统的相似性理论-量纲分析-过于粗糙，没有能够反映出湍流这一非平衡系统的特性。基于对称破缺的新的相似性理论，也就是本文要介绍的结构系综理论，顺利实现了这一突破。

2008年以来，我们在北京大学开展了结构系综理论的研究，力求从固壁所产生的基本对称性原理出发，来挖掘壁湍流所存在的公共物理机理。经过近十年的探索，结构系综理论在搭建这一应用基础研究框架上取得了系列的进展，完成了从基本原理出发的规范壁湍流刻画[17-18]，并将理论成功应用于一系列复杂效应流动的高精度刻画中，并在面向工程湍流的精准湍流模型研究当中，取得了突破性的进展。

2009年，首次以应力长函数(序函数)封闭了RANS方程，实现了对平均速度剖面以及流向湍动能剖面的精确刻画，提出以结构系综理论构建一个跨越基础研究与工程模型开发的桥梁的目标[19]；之后，系统的阐述了从第一原理出发刻画壁面约束产生的对称性的理论框架-序函数分析方法[19-20]。后续一系列研究逐渐表明，这一分析框架能够成功的刻画一系列壁湍流流动，并为工程湍流模型的开发提供了新的理论方法；2012年，基于李群分析方法给出了基函数表达式背后的拉伸不变性原理[21]，应用这一分析方法，在之后的研究中，对卡门常数、圆管与槽道流动定量区别、边界层流向发展等壁湍流研究的核心话题给出了深入的探索[22-23]；2013年给出了规范壁湍流中基于多层结构的普适卡门常数(κ=0.45)新定义方法[24]，由此对壁湍流研究的一个核心话题——卡门常数的普适性提出了独特的见解；2016年，构建了对全流域和全Re数相似律的解析湍流边界层理论[23]，同时给出了平板边界层，槽道，圆管三类规范壁湍流的统一表述，并且用从理论上明确了圆管与槽道不同几何外形变化对流动的影响[25]，以及首次给出了边界层湍动能理论[18,26-27]；2017年，在经历与国际湍流界的充分交流和争论以后，该研究的核心成果-基于李群拉伸不变性原理的壁湍流理论终于在 JFM杂志发表[17]；次年(2018年)，推广到全部雷诺应力分量(即包含对平均速度剖面和动能剖面的统一理论)得以完成并发表[18]。至此，结构系综理论的理论研究框架基本建立。

在2010年由壁湍流的几位国际著名学者所发表的一篇综述文章中[12]，平均速度剖面的Re相似性、粗糙表面的相似律、对数律的流域范围和卡门常数κ的普适性被列为几个未解决的核心话题。结构系综理论对这四个问题都作出了完整的解答。

已经有研究成果表明，结构系综理论的研究框架是普适的，能够延伸到各类非规范流动研究，适用于对各种复杂效应的物理刻画，如壁面粗糙元效应[28]，可压缩效应[29]等；并能够完成包含多种流态的热对流系统(RBC, Rayleigh-Benard Convection)的平均剖面的刻画[30]。其中值得指出的是，对于大雷诺数流动，黏性尺度变得非常小，以至于小雷诺数下近似光滑的壁面，也会出现粗糙元效应[12]。另外，在高超声速飞行器设计中，可压缩效应是重要的物理因素。研究证明，以规范壁湍流的多层结构函数形式，引入参数的缓慢变化，可以对这些复杂流动给出准确刻画。这说明结构系综理论所阐述的对称性原理是普适的。

另外，研究证明，结构系综理论是分析现有工程湍流模型的有力工具，它修正了k-ω模型，给出能够同时精确预测平均速度剖面和流向湍动能剖面的SED-k-ω模型[7,27]，并产生了能够预测多种复杂工况(翼形、转捩等)新型代数模型(SED-SL模型)[31]。后者正在完善过程中，以实现能够直接服务于工程实践的初衷。

壁湍流的结构系综理论是Prandtl-von-Karman的对数律理论的延伸。那么，它是如何挖掘壁湍流中的对称性的？层流平板边界层满足严格的拉伸不变性(即普拉修斯解)，在湍流状态下，脉动的出现必然导致原先的对称破缺，产生一种新的对称性。结构系综理论首先寻找合适的相似变量，追随物理学家朗道，把这样的变量称为序函数。与湍流脉动的特征尺度相对应的长度序函数进入我们的视野，被认为是能够反映系统对称破缺的相似变量。结构系综理论认为，一旦找到序函数，即找到最简洁的刻画壁湍流中对称破缺的解析表达。这一思想在拥有湍流边界层的数值解的今天就变得非常容易贯彻，果然，我们从大量DNS数据分析中确认了存在满足这一特性的长度序函数，它具备连乘的幂次解形式(SED基函数)。如光滑圆管的雷诺剪切应力长度序函数的表达时由内区解(y+的函数,上标+代表用壁面单位归一)和外区解(r的函数,r为离边界层边缘的距离,或圆管槽道半径)的乘积来表示：

l12(y+;r)=Φ(y+)Ψ(r)

(5)

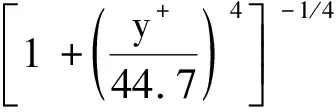
(6)

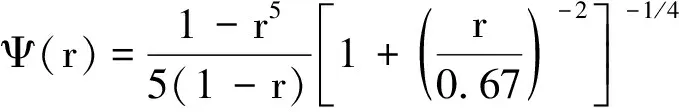
(7)

(6)与(7)式中的基本函数满足一个广义李群拉伸不变性预设，这是从严格李群拉伸对称性的幂次解(单层结构)通过对称破缺演变而来的多层结构，这是非平衡系统的特色，即所有的非平衡系统(例如湍流)都拥有相对于平衡态系统的某种对称破缺。于是，结构系综理论从基本原理上给出了湍流系统的特征。由于包括层次跃迁的广义李群拉伸不变性具有普适的形式(如公式(6)和(7)中的跃迁函数拥有相同的形式)，这便构成一个在壁湍流中的普适物理原理，即对称破缺产生多层结构的原理是普适的。或者说，多层结构的解析表达在壁湍流中是普适的。结构系综理论揭示的这一普适原理，是对Prandtl-von-Karman的对数律理论的极大的拓展，在未来描述复杂工程壁湍流时将会产生重要的影响。

这一描述也是对传统对称性分析方法的发展。应用最广泛的对称性分析就是量纲分析，其背后的原理就是关于物理基本变量(如时间，空间，质量等)的拉伸不变性。前面提到，现代工程湍流模型在封闭RANS方程时主要就是运用了量纲分析，所以湍流模型满足了物理基本变量的拉伸不变性。但是，我们认为，复杂流动的出现对应的是一系列的对称破缺，仅仅从满足对称性的约束出现，是无法对复杂流动的物理开展细致描述的。结构系综理论所引进的广义拉伸对称性假设，跳出了传统对称性分析的框架，大胆地对各类壁湍流的对称破缺的普适机理开展探索。在过去的几年中，我们已经针对几类规范壁湍流系统开展了严格的验证。对于规范壁湍流的平均速度剖面的刻画，普遍达到99%的精度，对于动能也基本达到95%的精度，这是前所未有的。这样的高精度的一个意义是其多层结构的物理描述参数对流动条件的高度敏感，从而这些参数的变化可以描述更加复杂的流动。有迹象表明，函数形式(6)与(7)不仅仅对于规范壁湍流严格成立，而且普遍适用于更加复杂的流动，只需使参数随着流动的物理条件而缓慢变化(它们于是构成所谓的慢变量)。这一面向对称破缺的对称性分析将如愿完成对于湍流这一非平衡系统的描述，就像非平衡态热力学一样。后者是基于热力学参数(温度、压强等)的时空演化，而复杂壁湍流的刻画将表现为普适多层结构参数在空间的变化。实践证明，这样的演化所给出的是对各类复杂流动的细致精确的刻画。于是，一个能够在普适原理指导下开展复杂流动的精细多层结构刻画的方案诞生了，这就是结构系综理论的意义。

上述理论建构与主流湍流研究的DNS和LES形成了互补。DNS和LES所给出的是对于特定流动参数下的流场的精细刻画，而结构系综理论所构建的是不同流动参数的流场之间的相似性关联。一个大家普遍关注的问题是，为什么数十年来DNS和LES的长足进步，没有能够为工程湍流模型的建构提供直接的支撑？这是因为，对于DNS和LES的大数据分析，一直沿用的是传统的过于注重脉动结构的分析方法，缺乏对于壁湍流整体(相似性)运动规律的探索。结构系综理论为解决这一问题提供了一个出路：壁湍流的公共原理来自于固壁带来的对称性约束，DNS和LES的大数据可以来验证这一命题(即验证(6)与(7))。而一旦通过检验，则可以遵循系统的方法确定多层结构参数，从而确定湍流涡黏系数沿垂直方向的分布，于是直接封闭RANS方程，用于工程计算。于是，结构系综理论在DNS(LES)和RANS之间构建了一个桥梁，背后所依据的原理是固壁所带来的广义拉伸对称性(或对称破缺原理)。

于是，结构系综理论把湍流理论的另外一对关键的二面统一起来了：普适性的原理(简单)与具体流动的多层结构参数(复杂)。定义序函数所依据的原理是简单的，函数形式也不太复杂(连乘的形式)，而多样化的具体流动体现在多层结构的参数随空间的变化上。前者是理性的结论，是简单的，后者则是由经验数据所提供的。对湍流复杂系统的描述需要的是理性与经验的统一；实践证明，脱离经验的湍流理论是没有价值的。

2.2 结构系综理论的技术路线

结构系综理论研究的技术路线是，用序函数分析方法从实验和计算数据中提取流动中的对称破缺的物理信息。它包含如下几个步骤：(1)定义合适的序函数，验证壁面约束的广义拉伸不变性(即普适的对称破缺)；(2)从数据中分析提取序函数的多层结构参数；(3)针对流动条件的变化，决定多层结构参数的变化规律，这是该流动的物理信息。具备如此精细变化信息的多层结构描述，既可以给进一步的基础研究提出物理机理的命题，同时可以直接用于构建工程湍流模型。

序函数的出现反映了流动中的对称性的影响。验证对称性(或对称破缺)行为与定义序函数是一件事的二个方面，前者属于基础研究关心的话题，后者则直接有工程意义。以往湍流模型的研究是寻找脉动量与平均量的关系，实践证明，对于不同流动，不存在普适的关系。但这里我们寻找的序函数是一类新的相似变量，它反映的是边界(固壁)的影响，所以它对于一类流动可能是普适的。实践证明，这一概念具有很强的可拓展性。例如与不可压缩边界层相比，可压缩边界层中不仅存在动量输运问题，还存在能量的输运问题，因此，在可压缩流动中不仅存在主宰动量输运的应力长函数，还存在主宰能量(内能或者温度)输运的能量长函数。

在壁湍流中所发现的最为重要的序函数是长度序函数，如应力长函数，它刻画的是湍流脉动涡结构的特征尺度。另外，可以证明，序函数的比值仍然为序函数(正如无量纲量的比值仍然是无量纲量一样)。另外，还有一类完全受壁面控制的量(如总应力，总热流等)，壁面对它们拥有强烈的约束(如壁面为常数)，这些量与壁面量之差也满足序函数的性质。

序函数确定以后，确定参数是定量刻画流动细节的一步，也是提取具体流动的物理规律的关键一步。序函数中的参数构成对具体流动的精细刻画。于是，针对不同流动确定序函数参数的数值则构成对于流动的个性化描述的重要内容，也是对于具体流动开展定量研究的内容。进一步针对一系列流动来考察序函数参数的变化，并给以物理解释，则成为揭示流动物理机制的重要内容，为各种工况下开展精准的工程计算创造条件。

这里，我们简单介绍多层结构参数的确定过程。规范壁湍流的应力长函数中的参数已经通过与DNS数据的比较被完全确定下来。例如光滑圆管中的应力长的内区函数的一般形式是：

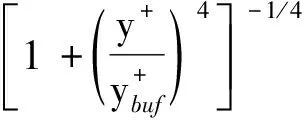
(8)

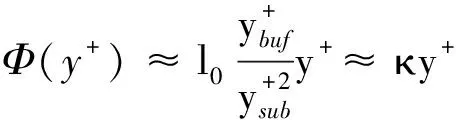
(9)

这里，κ就是著名的卡门常数。代入上述参数值，我们得到κ≈0.45，这是我们依据最新的实验和计算数据对著名的卡门常数的重新标定，比过去所确定的数值(0.41)大了10%。值得指出的是，这个数值对槽道、圆管和边界层是普适的，不像一些文献中对于不同的流动需要不同的卡门常数[32]。在更加复杂的流动中，例如存在压力梯度效应的翼型表面流动，或者存在密度和温度变化的高速可压缩边界层壁面附件的运动，这些参数会有变化，卡门常数也因此会变化。结构系综理论给出了确定卡门常数的系统性的方法[24]。

参数的确定过程，再一次采用了基本原理与经验事实相结合的思路。给定序函数之后，有两种确定参数的方法，一种是对DNS数据进行分析，通过局部近似逐层地确定参数的取值；另一种是基于已有的经验，考虑从已有流动到新的流动中多层结构物理的变化，人为地设置多层结构的修正，将新的预测与实验或计算数据进行比较，来确定新参数的有效性。前者为先验地确定参数(必须有充分精确的DNS数据)，后者为后验地确定参数，它的意义是不需要很多的测量数据，因此可以适用于更多的复杂流动。两种方法的交叉使用是最有效的。

由于序函数的参数具有明确的物理意义，因此，结构系综理论的研究引发了一系列基础研究新话题。例如，在流场中寻找与应力长函数所对应的流动结构，或者考察多层结构某一层厚度变化背后的物理机制(涡运动、能量平衡机制)，等等。而物理意义明确的参数，又方便工程师在应用时进行调节。只要直观上对流动物理结构的变化有所认识，就可以对工程模型中的参数进行调节。这样，基础研究与工程研究就可以进行深层次的互动，工程研究者可以针对更多更复杂的流动提出更多的序函数，而基础研究者则可以针对新的序函数考察其背后的对称性，及其参数变化的物理机制。总之，对物理机理的理解与对复杂流动的预测能力能够同步提高。

2.3 对传统湍流模型的改进

工程上应用广泛的湍流模型，实际上已经隐藏了多层结构的假设(因为这是壁湍流中客观存在的物理结构)。借助结构系综理论的序函数分析方法，可以细致地考察湍流模型中的多层结构设置。这一分析从局部平衡关系出发，推导传统湍流模型参数与SED多层结构参数的关系，从而根据多层结构与物理条件之间的关系，给出对传统湍流模型的修正。例如，对于k-ω模型的分析和修正亦已完成，下面对之进行一个简单介绍。

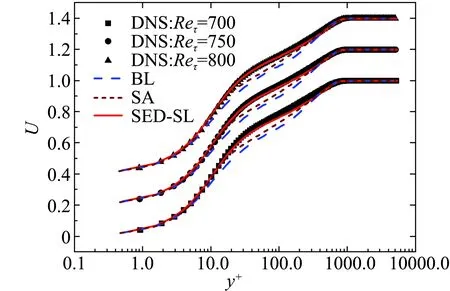
针对Wilcox2006年版的k-ω模型[4]开展分析，我们发现需要开展三个修正：第一，修正卡门常数为0.45；第二，需要引进非线性涡黏系数，来修正圆管中心区的对流效应；最后，需要引进一个新的介观区，其中出现湍流耗散的奇异标度，它会带来湍动能的第二个峰值。通过三个修正，首次给出了能够同时高精度地预测平均速度(图1)和湍动能剖面(图2)的新型的SED-k-ω模型[7,27]。

有意义的是，这里介绍的多层结构分析方法可以同时给出湍动能方程的解析表达，从而建立模型经验参数与多层结构参数之间的定量关系，给出具备明确物理意义的湍流模型参数化方案。而且，可以通过逐层考察多层结构信息在模型中的表达，输入准确的多层结构信息，完成对现有湍流模型的优化。

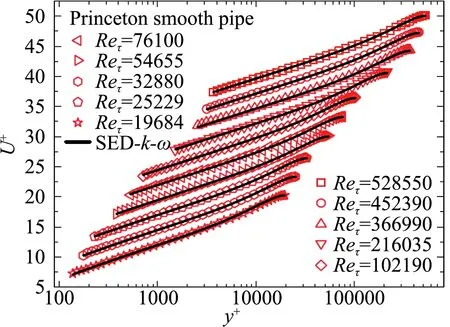
图1 SED-k-ω平均速度剖面预测结果与实验数据的比较，红色的点是普林斯顿超级圆管实验数据，黑色的线是模型计算结果[7]Fig.1 Comparison of the mean velocity profiles predicted by SED-k-ω model with experimental measurements. The red open symbols are from Princeton supper pipe experiment. The black lines are from the SED-k-ω model [7]

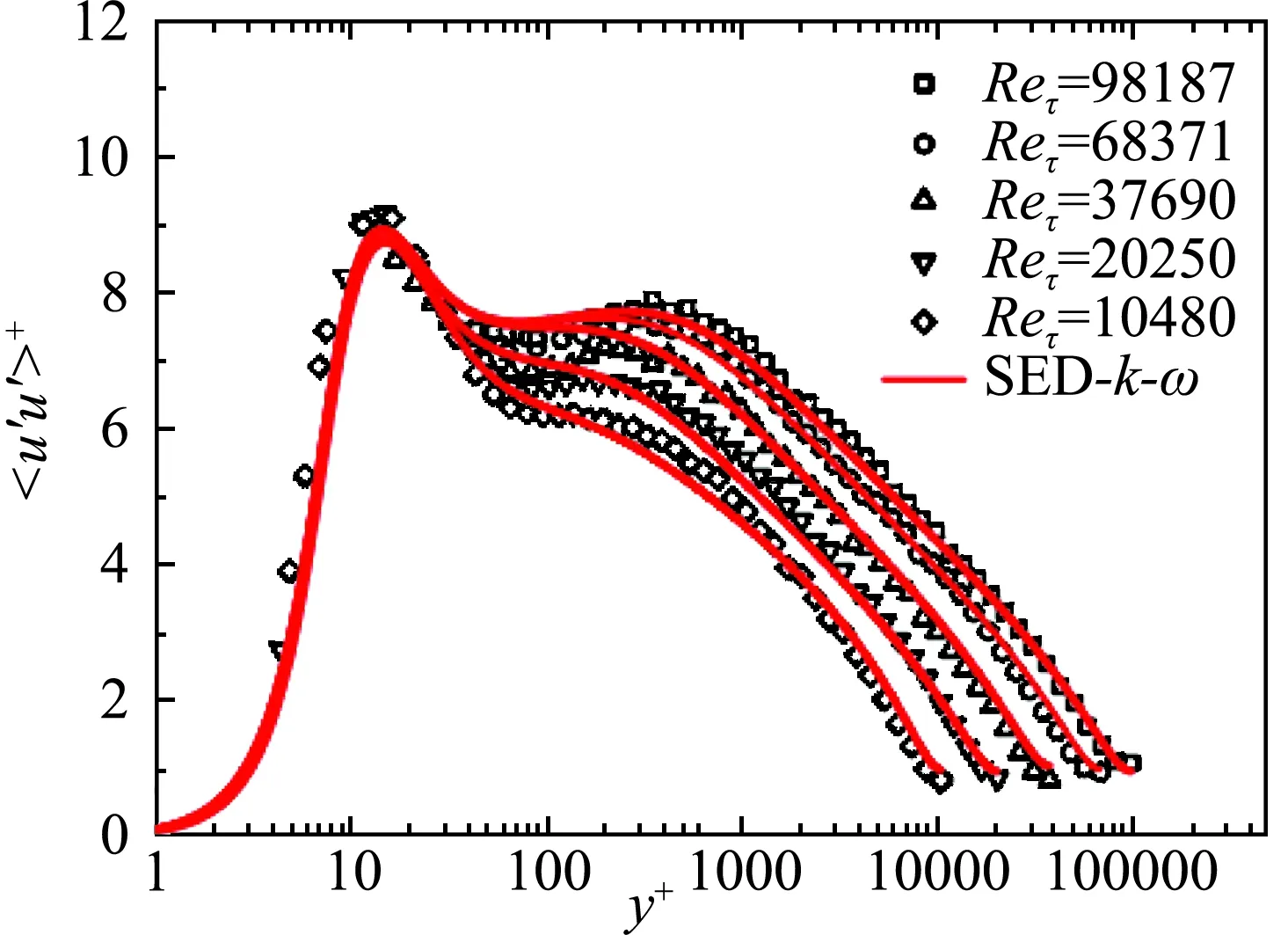
图2 SED-k-ω动能剖面预测结果与实验数据的比较，红色的点是普林斯顿超级圆管实验数据，黑色的线是模型计算结果[27]Fig.2 Comparison of the kinetic energy profiles predicted by SED-k-ω model with experimental measurements. The black open symbols are from Princeton supper pipe experiment. The red lines are from the SED-k-ω model[27]

2.4 基于结构系综理论的湍流新模型: SED-SL

由于结构系综理论可以从应力长函数给出涡黏系数的完整表达，于是就可以直接给出一个RANS方程的代数模型，这就是新发展的SED-SL模型(SL是应力长stress length的开头英文字母)。我们在下一节着重介绍SED-SL模型应用于刻画实际流动的一系列结果。而这一模型的诞生，首先解决了一个重大问题，即对于从层流到湍流的转捩(见第3.1节)，其次，在一系列航空航天应用相关的流动(翼型、机翼等)获得精度远超出传统湍流模型的结果。

结构系综理论对湍流边界层给出了清晰的多层结构的物理图像，因此不断将基于结构系综理论的湍流模型应用于更加复杂的流动，有望为工程实践提供计算快捷准确(建立在准确的应力长函数基础上)，同时又可以不断应用于新的流动的计算工具。这是一个与DNS和LES相互补充、共同推进的过程：即通过相关的DNS或LES的研究，总结出具体复杂流动的物理机制和多层结构的参数变化规律，从而产生精确的符合Re相似性的工程湍流模型。

3 非平衡流动的结构系综理论

工程实践中面对的许多复杂流动是非平衡流动。但是，对于工程设计而言，重要的物理量依然是这些流动的统计定常性质，因为所有的工业产品都必须长期稳定地运行。因此，结构系综理论本质上是可以讨论这些流动特性的。例如从层流到湍流的转捩，以及分离流动。这些流动中出现了新的对称破缺，但是壁面约束依然存在，我们只是需要确认，对应于非平衡流动的对称破缺是否可以由多层结构参数的缓慢变化来刻画？这就是结构系综理论应用于刻画非平衡流动的总的思路，实践证明，对于相当大一类的非平衡流动，这个思路不但是可行的，而且导致了新型、精确的工程湍流模型的产生。

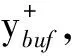
下面，我们针对一些具体的研究问题，介绍如何运用结构系综理论的思想和方法，取得对非平衡湍流系统的更加精确的刻画。

3.1 对转捩模型的创新

对转捩过程的建模始终是空气动力学研究中的一个重点，依据第二届国际阻力预测会议 (drag prediction workshop, DPW)上Rumsey等人的报道，影响CFD计算结果的前三要素是湍流模型、转捩模型以及网格，其中湍流模型占据约15%，转捩模型占据约11%[33]。Durbin(2018)[34]指出：将转捩过程嵌入到RANS模型中对于工程师来说是一个非常大的挑战。

当前最受重视的是基于局部变量的转捩模式，一种形式是引入一个关于间歇因子γ的输运方程，其基本假设来自于Warren和Hassan[35]，引进表达流场某一位置上保持为湍流状态的时间比例：

μeff=(1-γ)μnt+γμt

(10)

其中μeff为有效黏性系数，反应出从层流到湍流转捩过程中流动黏性系数的变化。其值在转捩结束后应与湍流黏性系数相等，而在转捩之前的区域，γ反应出层流边界层中不稳定扰动波的影响。比较有代表性的转捩模型为Menter[36]提出的γ-ReθT转捩模型，符松等[37]在此基础上提出了形式较为简单的k-ω-γ三方程转捩模型(其中k是湍动能，ω是单位耗散率，γ是间歇因子)，对原有转捩模型进行了优化，提出了统一的脉动动能输运方程，而间歇因子γ的输运方程为：

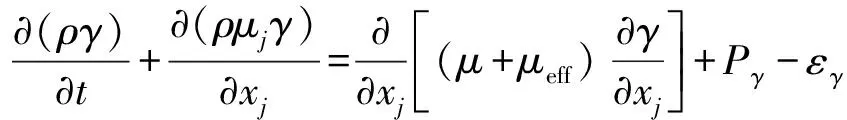
(11)

这里，方程右边最后二项分别为产生和耗散，它们的设置是借助了Dhawan和Narasimha从实验数据拟合所得到的经验公式。间歇因子的输运方程与动能和耗散率输运方程组成完整的方程组进行求解。这一模型可以对一类由第一和第二不稳定模态所激发的自然转捩过程预测转捩起始的位置，但依然由一个经验函数Fonset决定。这一模型的特点是能够应用于较宽的马赫数范围，从亚声速至超声速以及高超声速，对于流动转捩的捕捉效果都比较好。对于更一般的非自然转捩，则没有自洽的转捩预测模型。

当前，人们偏向于基于局部变量的模型，主要是考虑到对于复杂非平衡流动的适应性。但是，我们发现，基于局部变量的经验规律形式会比较复杂，这是因为它附加了从固壁前缘到转捩点之间的演化过程，而这一过程高度非线性，以及与物理工况相关(非普适)。由此产生的模型的复杂性很大，精度还不能令人满意，同时又不能对不同转捩机制(如来流湍流度，压力梯度，局部分离转捩，以及壁面扰动等)进行统一的刻画。所以，对于工程师来说，对流场开展转捩计算仍然是十分困难的事，更为困难的是高超声速飞行器边界层转捩问题，由于飞行状况的改变，涉及更多的复杂因素，Anderson[38]很早就指出，高超声速转捩的“雷诺数”ReT，与边界层外沿的马赫数、 为自由来流的单位雷诺数、飞行器头部曲率半径、壁面温度、来流总温、迎角、壁面质量流量(由于吹吸或烧蚀)、物面粗糙度、环境因素、表物面外形特征(比如圆锥的半锥角)、压力梯度、横流速度梯度、化学反应特征时间和程度等十三个因素有关。近年来，随着高超声速飞行器研究的开展，人们发现，对于不同的工况，上述因素所起的作用没有明显的规律，风洞实验、飞行试验、稳定性分析和数值模拟等研究方法，都仅能从一个或少数几个方面开展研究[39],并且研究发现，很多因素的影响上存在相互矛盾的地方[40]，我们认为，适用于低雷诺数和高超声速转捩的湍流模型研究，需要在基础理论认识上产生实质性的突破。结构系综理论在抓住壁湍流基本原理的基础上，能够以慢变量参数的缓慢变化，研究多种复杂效应下壁湍流流动，在转捩模型研究中取得了突破性的进展。

下面，我们介绍结构系综理论对于转捩的刻画。从系统的角度看，转捩模型需要刻画的是一个系列的不稳定事件的综合结果，如果在系综层面上会发现其简单性。具体来说，在转捩发生前后的任何一个位置上，流场在垂直壁面的方向上都受到壁面的对称性约束。在层流区是Blasius对称性，在充分发展的湍流区则是SED理论所发现的多层结构对称性。从平板前缘开始，序函数在流向方向的变化应该是这二种对称性之间的转换。由于多层结构的对称性比较弱，可以设想一个从后往前的变化策略，即从多层结构变化到Blasius单层结构的模型。我们发现，如果令多层结构中的二个参数在流向也按照层流-湍流二层结构的方式进行如下变化：

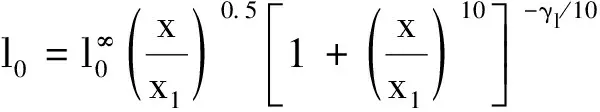
(12)

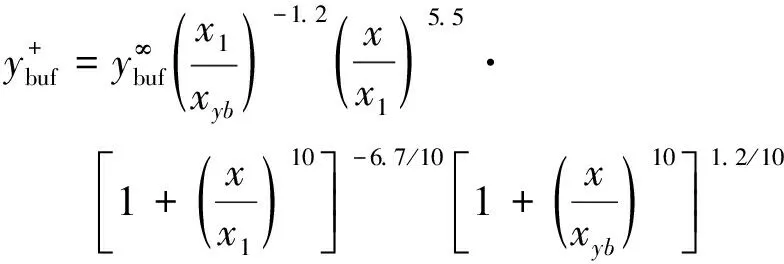
(13)

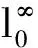
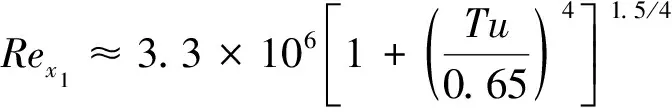
(14)

其中临界湍流度Tuc=0.65由图3中的数据拟合经验得来，它具有重要的物理意义，表征自然转捩与旁路转捩的分界线；在湍流度远小于0.65%时，Rex1≈3.3×106基本不变；在湍流度大于0.65%时，转捩位置与湍流度成简单的-1.5的标度关系。公式(12)和(13)中的参数相当普适，于是，就构成了(含转捩的)SED-SL代数模型。

下面，我们简单汇总SED-SL代数模型对一系列流动进行的计算结果，包括自然和强迫转捩流动(图3)、充分发展的极高雷诺数边界层(图4)和可压缩边界层(图5)等。SED-SL模型在这些算例中均取得了极好的计算效果。

首先对于不可压缩平板转捩流动，精确地刻画了整个转捩过程，如图3所示。一共对比了七组工况，其中四组实验数据，分别为S&K平板边界层转捩实验[34]以及T3系列平板实验[41-42]，两者都是测试转捩模型的基准实验。S&K实验的湍流度非常低，为0.18%，所以对应为自然转捩；平板边界层转捩T3系列实验则给出了零压力梯度平板流动受不同来流湍流度影响下的转捩剖面，分别为T3A-,T3A及T3B，自由来流湍流度分别为0.87%、3.5%和6.5%。不同来流积分尺度下对比的数据为Brandt等[41]所给出的DNS计算结果。

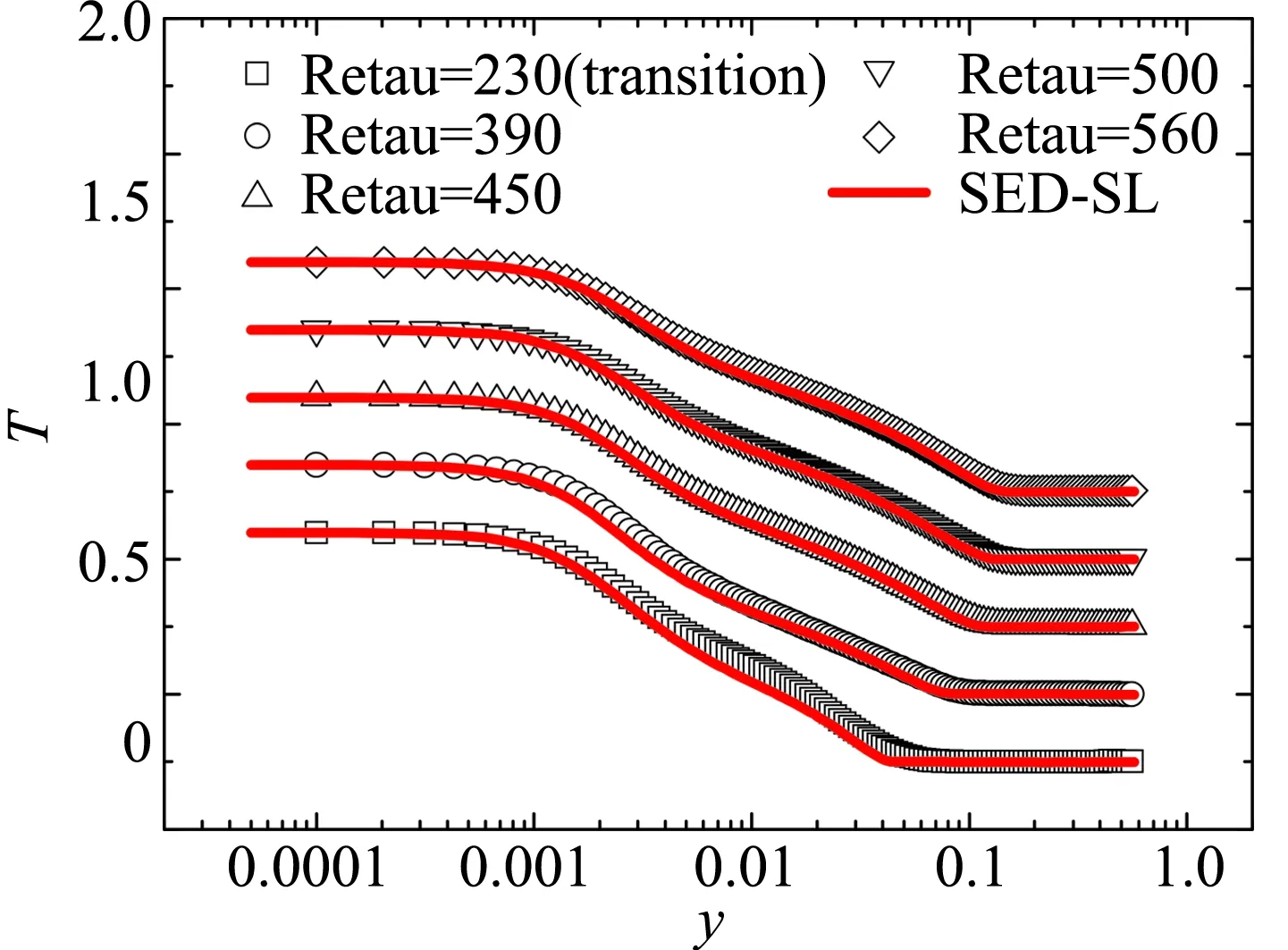
充分发展的极高雷诺数边界层速度剖面的对比如图4所示，对比的数据为普林斯顿超级圆管的边界层实验数据[43]。在不同雷诺数下，模型计算的结果与实验数据的每一个点的偏差都在2%以内，与实验测量的误差几乎等同。

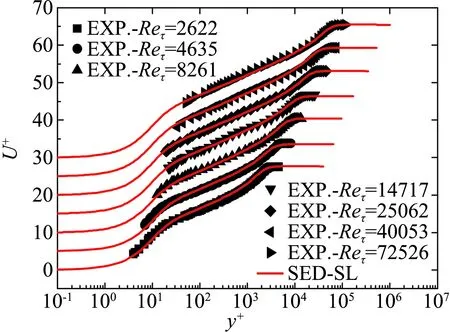
图4 SED-SL模型(红线)对充分发展的湍流边界层平均速度剖面的预测与实验数据(黑色点)的比较。结果显示，模型对实验数据在雷诺数全范围内实现了精确刻画[43]Fig.4 Comparison of the mean velocity profiles for fully developed turbulent boundary layers at available Reynolds number between SED-SL’s prediction (red lines) and experimental and numerical measurements (black filled symbols). Highly accurate descriptions cover the entire available range of the Reynolds number[43]

对于超声速和高超声速边界层流动，SED-SL模型同样能够对转捩以及充分发展区的流动行为进行精确刻画，如图5所示。对比的数据为DNS(Ma=2.25)可压缩平板流动的计算结果[29]。此DNS算例所加的扰动的方式为壁面吹吸扰动，对应地模型参数gamma1设置为20，转捩位置的设置与DNS所加吹吸扰动的位置一致。结果表明，SED-SL模型实现了对平均场剖面(速度，温度)的精确刻画。其中Retau=230处的剖面为转捩区的平均场剖面。计算的速度剖面及温度剖面与DNS数据的偏差都在5%以内。

SED-SL转捩模型似乎像先前曾出现的低雷诺数湍流模式，它最大的特点是方便与成熟的CFD湍流模型进行对接。有观点认为这只是一种数值上的巧合[31]。我们的研究表明，采用对转捩位置的新的表述，有希望建立更为简单精确的湍流转捩模型，在包括发动机在内的更为复杂的流场的研究中发挥作用。

3.2 翼型流动的预测

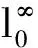
(a)

(b)

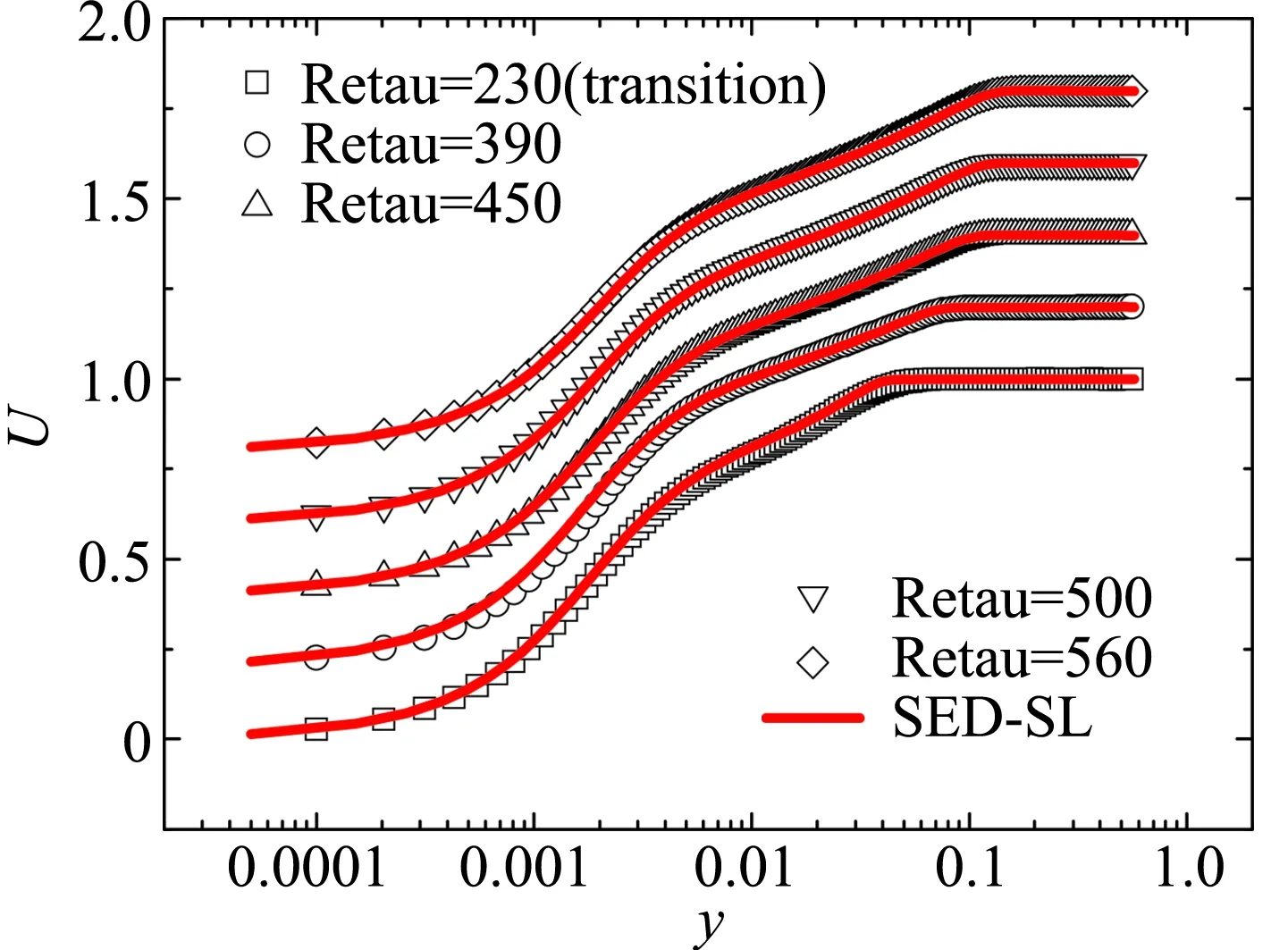
进一步，对于大迎角分离情况下的翼型流动，通过对应力长的多层结构形式进行少许的优化，增加能够反映逆压梯度效应的主流分离层以后，SED-SL模型同样获得对于大迎角分离流动的精确刻画。图8与图9展示了以NACA4412大迎角分离流动[46]和NACA0012临界迎角下周期性涡脱落流动[45]的计算结果。图8展示NACA4412尾部分离泡附近，六个位置处的速度剖面对比；图9则展示NACA0012在临界迎角发生周期性涡脱落时，某一时刻的平均场行为与相关DNS数据[47]的对比。

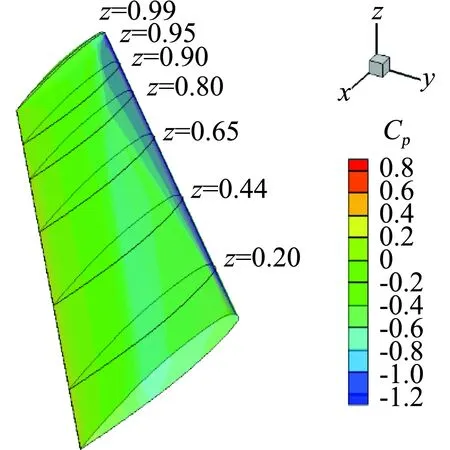
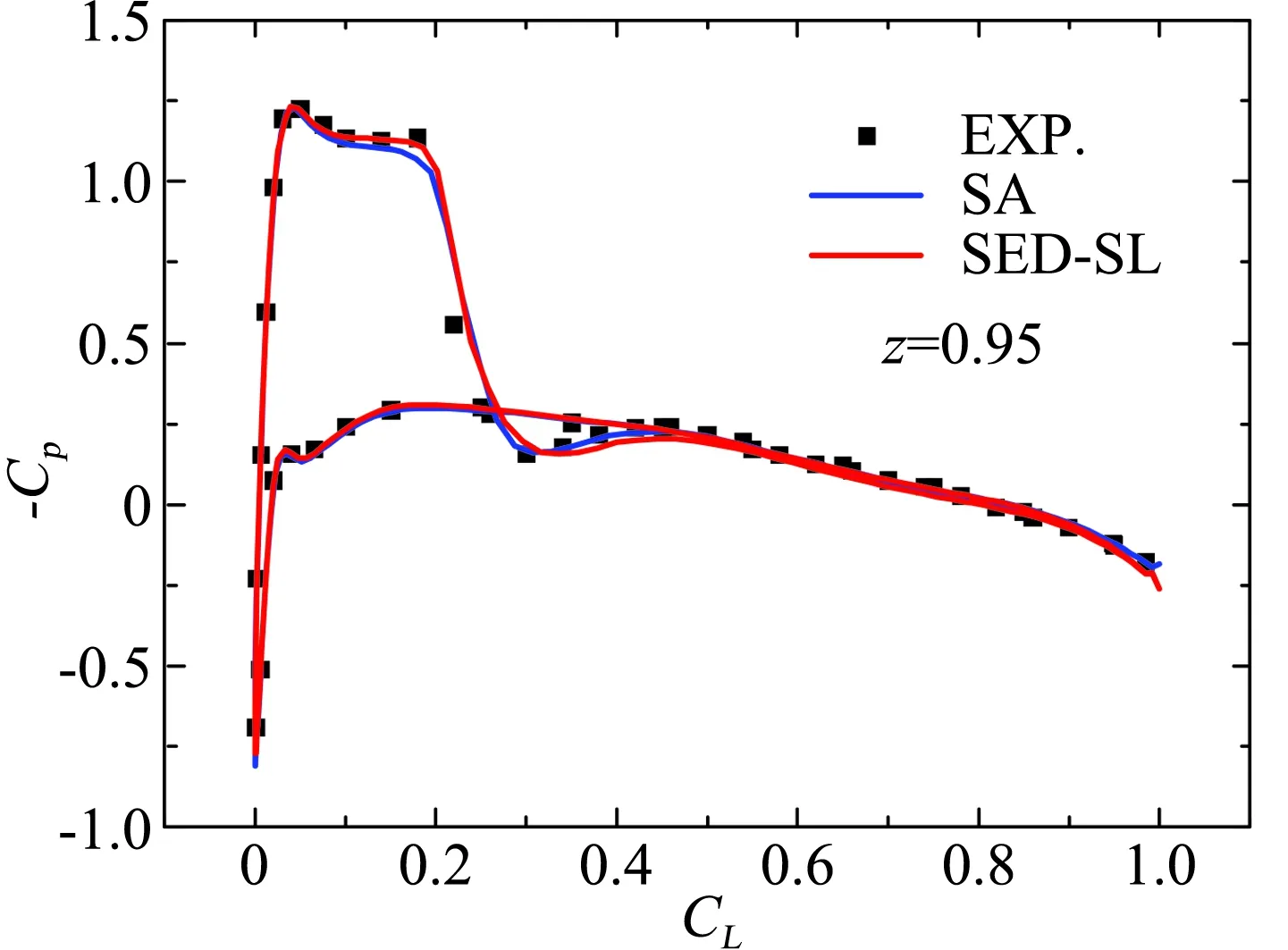
初步应用于三维机翼流动，SED-SL模型也取得了不错的结果，如图10所示。对比的数据为M6三维机翼实验数据，出自AGARD Report[48]，图10给出了某一位置处表面压力系数的对比结果。值得指出的是，该结果还可以继续优化，因为客观上存在横流，而横流对于多层结构所产生的影响是可以考虑的，最终能够实现对每一个剖面的激波位置的精确预测，而这一点目前任何湍流模型都做不到。

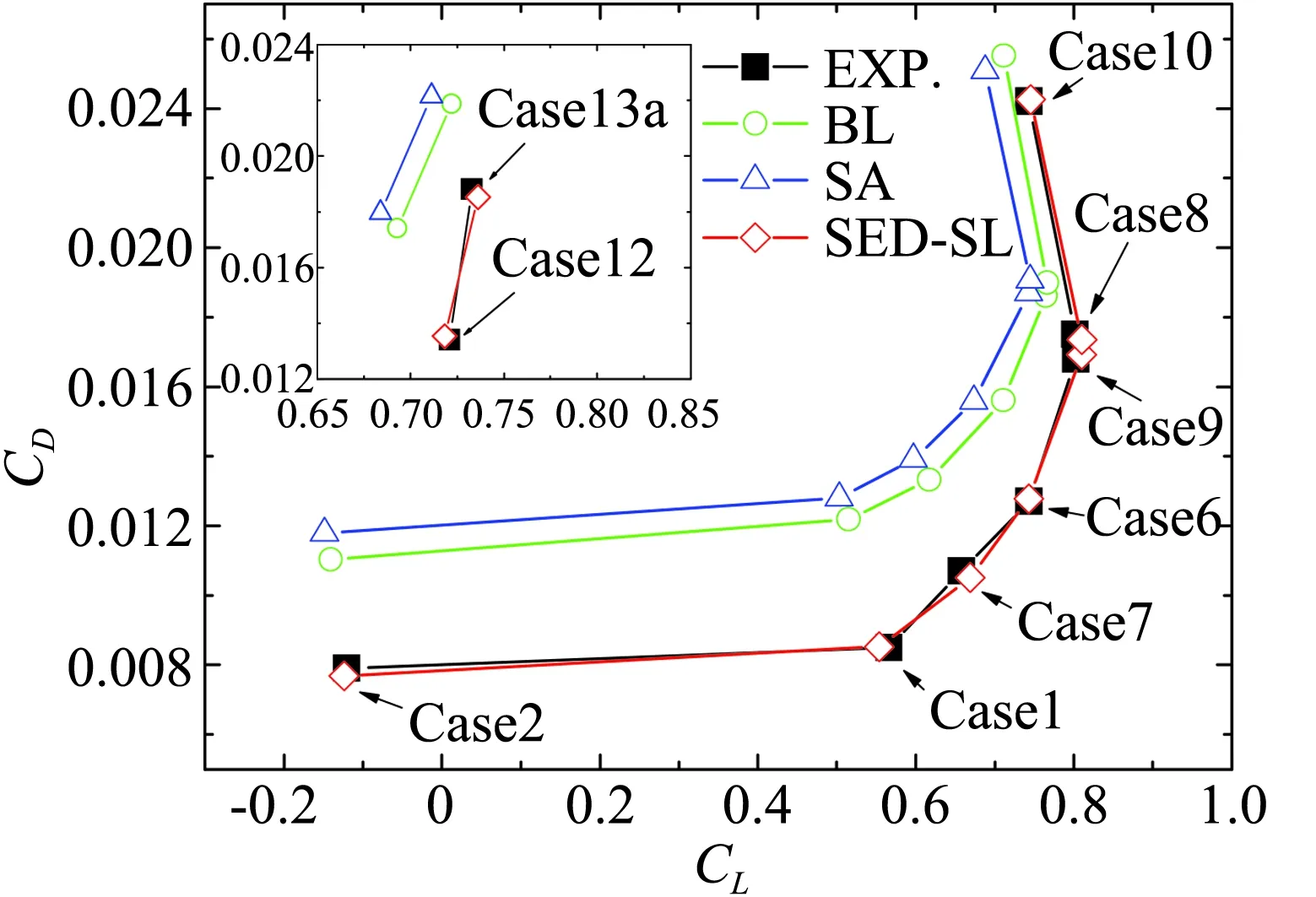
图6 RAE2822翼型不同迎角下的升阻力系数计算结果对比，黑点线是实验数据，红色是SED-SL计算结果，蓝色是SA模型计算结果，绿色是BL模型计算结果Fig.6 Comparison of lift coefficients (CL) and drag coefficients (CD) for RA2822 airfoil flow under different attack angles. Black filled symbols are experimental measurements[44]; red open symbols are from SED-SL model, green from BL model, and blue from SA model

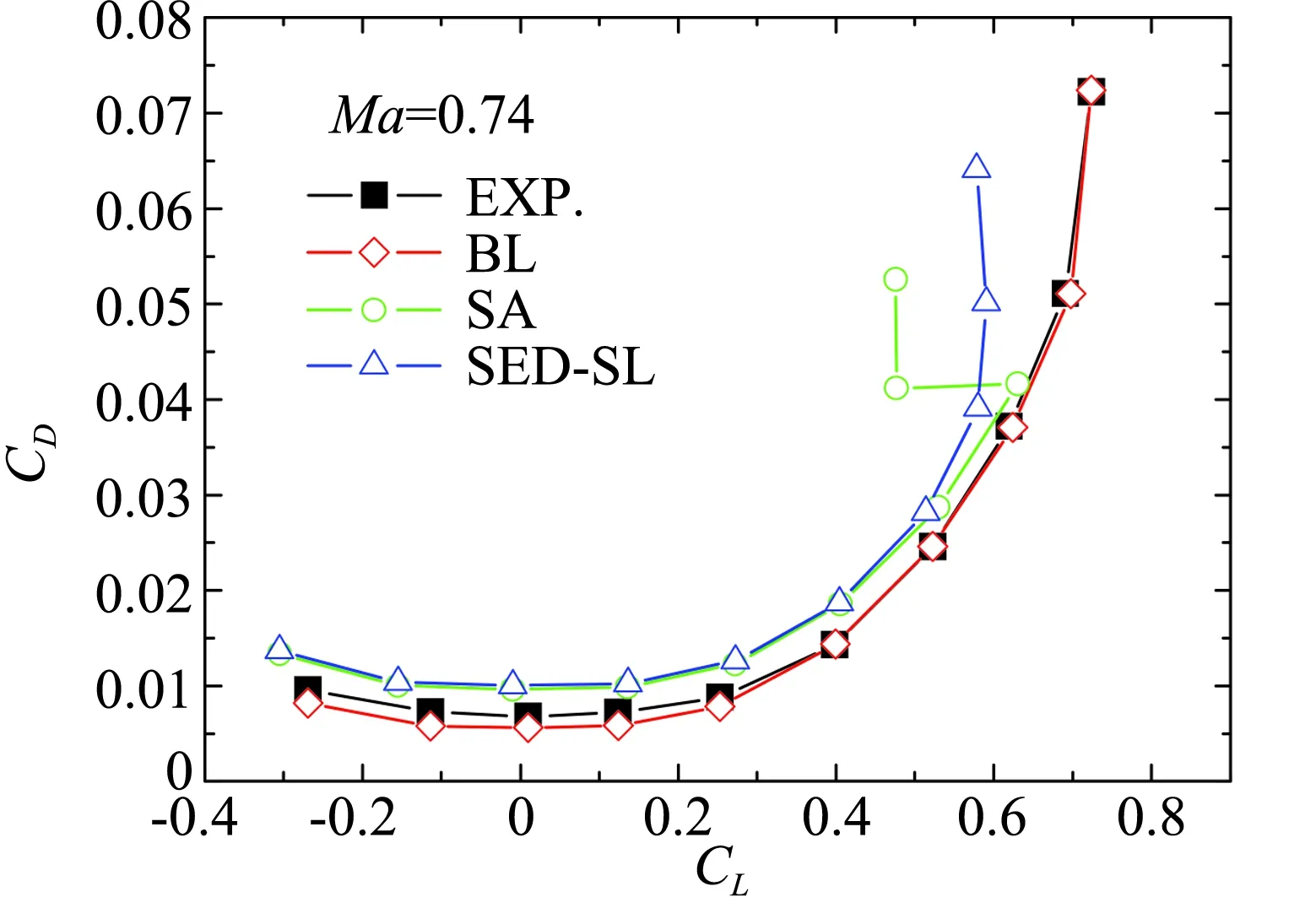
图7 NACA0012翼型不同迎角下的升阻力系数计算结果对比。图例同图6Fig.7 Comparison of lift coefficients (CL) and drag coefficients (CD) for NACA0012 airfoil flow under different attack angles. Legend is as same as Fig.6

(a) 实验测量(沿黑线)的分离区流场

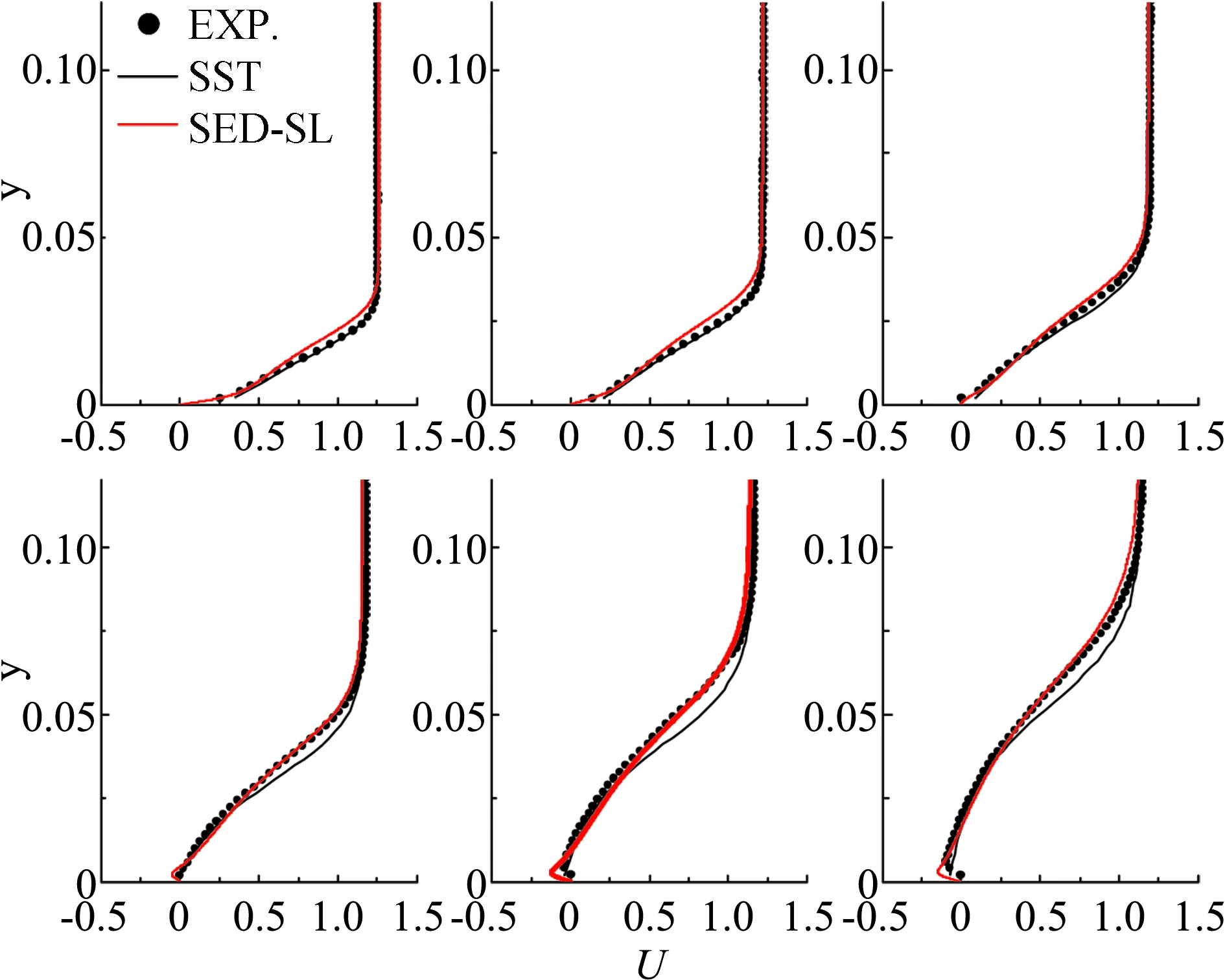
(b) 分离区不同位置((a)中黑线所标示)的平均速度剖面

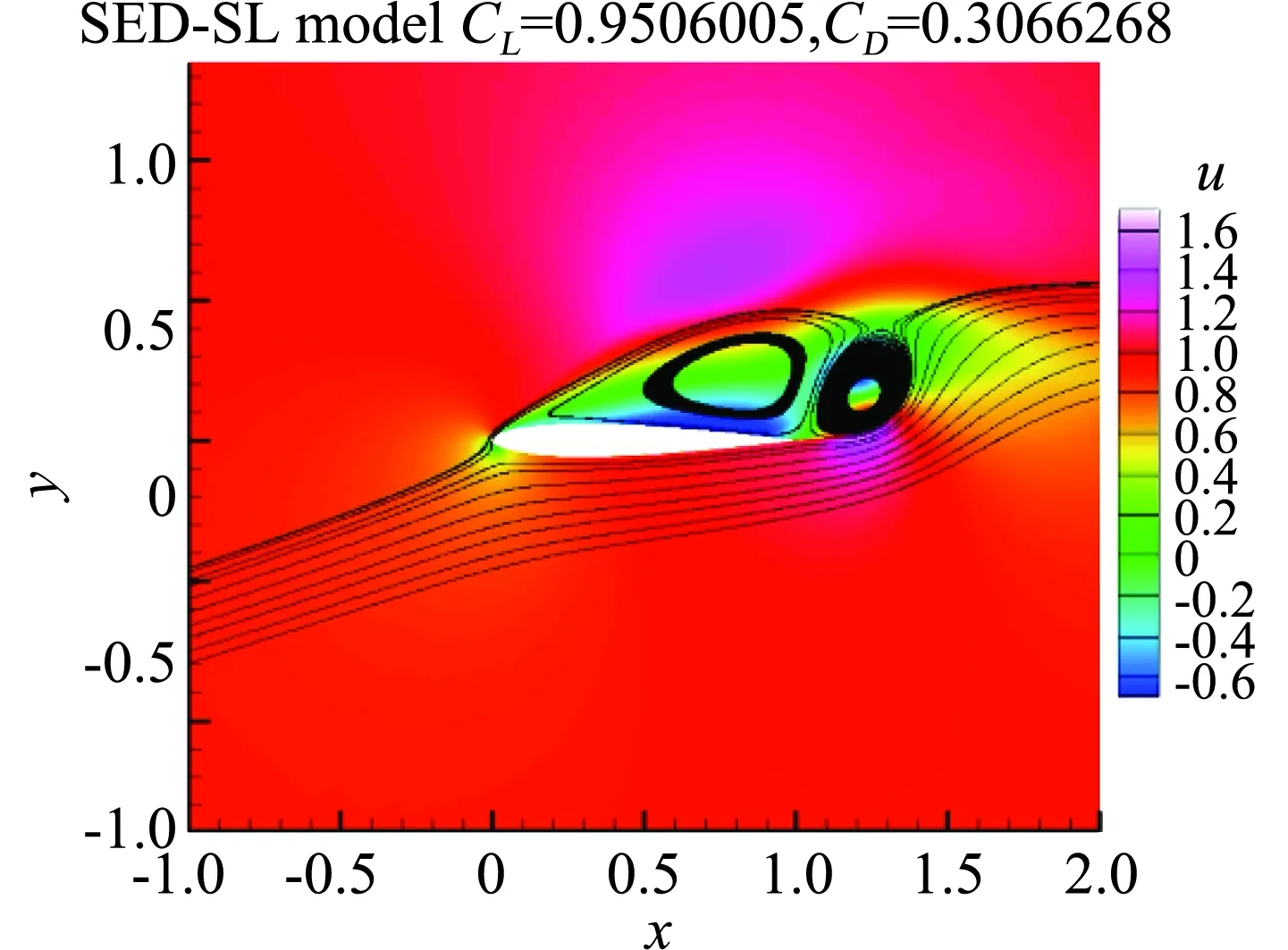
(a) SED-SL模型计算的非定常分离的某一瞬间的流场

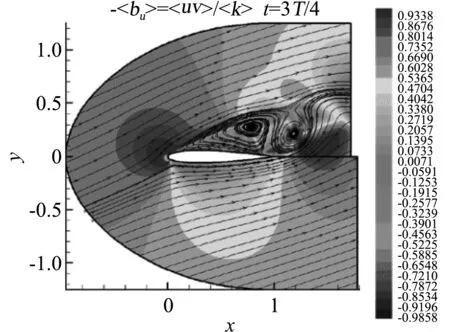
(b) 某一瞬态的DNS计算结果

(a)

(b)

SED-SL模型的成功具有示范性的意义。它表明，平衡流动中典型的沿垂向的多层结构可以通过引进多层结构参数沿流向(甚至展向)的变化来刻画非平衡的复杂流动。我们相信，这一思想可以推广至包含激波和分离等具有二维和三维效应的流动，因为只要固壁存在，系统的对称性依然是存在的，而更加复杂的流动行为可以通过引进参数的空间变化来实现。更加值得指出的是，一旦通过与实验数据的比较得到精确的力学效应(如升阻力系数)的预测的同时，我们同时获得了多层结构参数沿空间的变化规律，后者正是对湍流边界层的物理刻画。

SED-SL是一个简洁的代数模型，代数模型的关键点是以合适的函数(常见的是各类应力长函数)来刻画湍流黏性系数，从而封闭求解RANS方程，而确定这一函数的形式需要先验的对流动的特性有丰富的认识，而传统代数模型参数固定且无具体物理意义(混合长与流动结构的联系不明确)，这也是其适用范围狭窄，精度有限的原因。而SED-SL模型通过考察各种流动中多层结构的具体表达，发展个性化的精确的参数化方案，并由此可以给出流动的分类标准，从而对各类流动开展定量预测。这一模型发展的前景是乐观的。

3.3 超声速流动(气动力+气动热)的预测

高超声速飞行涉及到高马赫数低雷诺数带来的黏性干扰效应，同时还存在由于分子距离增大而带来的真实气体效应和稀薄气体效应。在这些应用问题中，突出的是对高速飞行所带来的气动加热问题的预测。真实的情况还涉及到由此带来的振动激励、离解、电离、化学反应等一系列效应，要完成对这一系列效应的精确预测，沿着传统的修修补补的思路前进是难以实现大突破的，需要从理论层次上探索这些现象背后的普适物理原理[1]。这里我们聚焦在关于热流的预测问题。

结构系综理论认为，在可压缩边界层运动中，不仅存在决定动量输运的应力长函数，而且拥有针对能量(内能)输运的温度长函数，它们的定义如下：

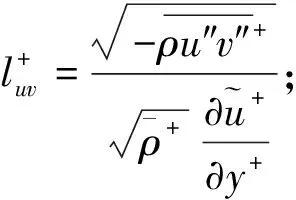
(15)

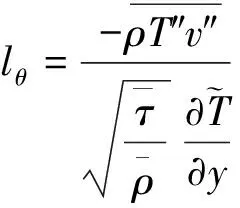
(16)

由于两个过程都受到壁面的约束，因此它们都满足广义李群拉伸对称性。实践证明，这些函数是分析可压缩边界层DNS数据的有力工具。例如，吴斌等[29]发现，在引入温度加权因子之后，

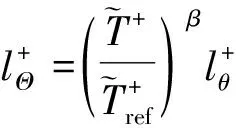
(17)

动量方程的总应力和能量方程的总热流在边界层外区具有相同亏损形式的拉伸不变解，也同样存在与规范壁湍流类似的多层结构。这一发现给出了一个雷诺比拟理论[29，49]，完成了对平均速度和温度剖面的精确刻画(详见参考文献[28])。

引入广义雷诺比拟[49]，SED-SL模型可以开展对于热流的预测，构成对可压缩平板流动的完整预测框架[45]。如图11～图13所示，涵盖的流况包括存在热流的可压缩平板流动DNS算例(图11)和实验流动(图12)，以及高超声速尖锥流动实验算例(图13)。

对于存在壁面热流的可压缩平板流动，以Ma=4.5的冷壁算例为例，图11给出了模型计算的不同流向位置处的平均速度剖面以及平均温度剖面与DNS数据[29]的对比，可以看到SED-SL模型预测与DNS数据的偏差在5%以内[31]，预测精度远高于BL以及SA模型。

(a) 平均速度剖面

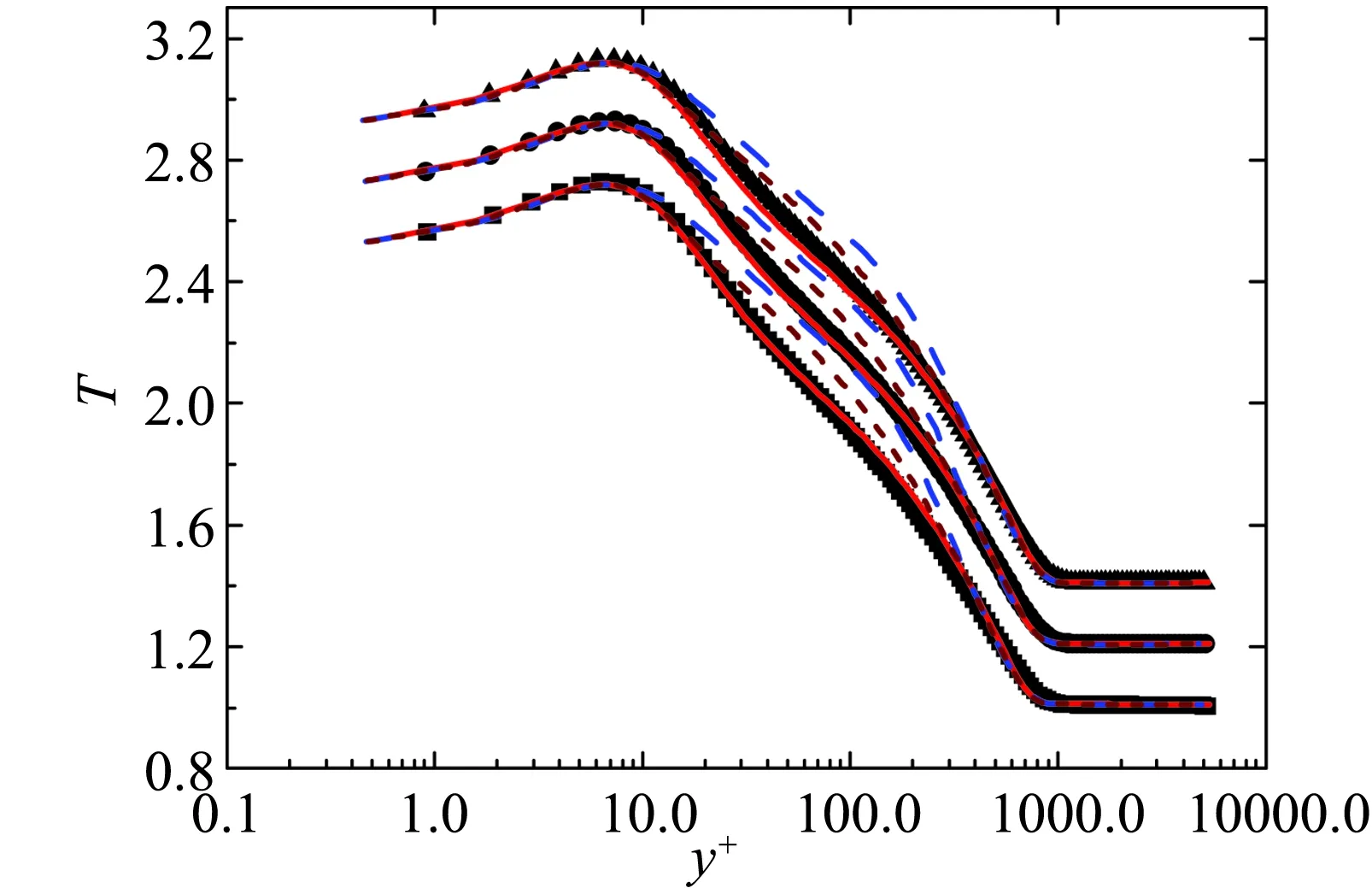
(b) 平均温度剖面

对于存在壁面热流的可压缩平板流动，对比参照的实验算例为Mee提供的超声速风洞实验结果[50]，包含马赫数5.5～6.3，雷诺数1.6×106～4.9×106冷壁下四个自然转捩的算例，来流湍流度为0.4%，壁面温度为常温300 K，其他参数如表1所示。计算结果如图12所示，可以看到SED-SL模型对于不同来流雷诺数下的热流转捩过程都进行了细致精确的刻画。

表1 超声速平板实验算例的参数设置Table 1 Parameter setting for case of supersonic plate experiment

对于超声速尖锥流动，计算对比的实验数据为NASA兰利研究中心在马赫数6超声速风洞所测量的数据[50]，包含八组不同流况下的尖锥流动数据。尖锥模型长635 mm，半顶角为5°，前缘鼻尖的钝化半径为0.002 54 mm。实验雷诺数的变化范围为(0.3～2.03)×107，壁面温度为来流总温的0.59倍，壁温与无穷远温度的比值为4.838(冷壁)，来流湍流度为0.4%，具体流动参数如表2所示。壁面热流的计算结果对比如图13所示，SED-SL模型同样实现了对于不同来流雷诺数下壁面热流的精确刻画。

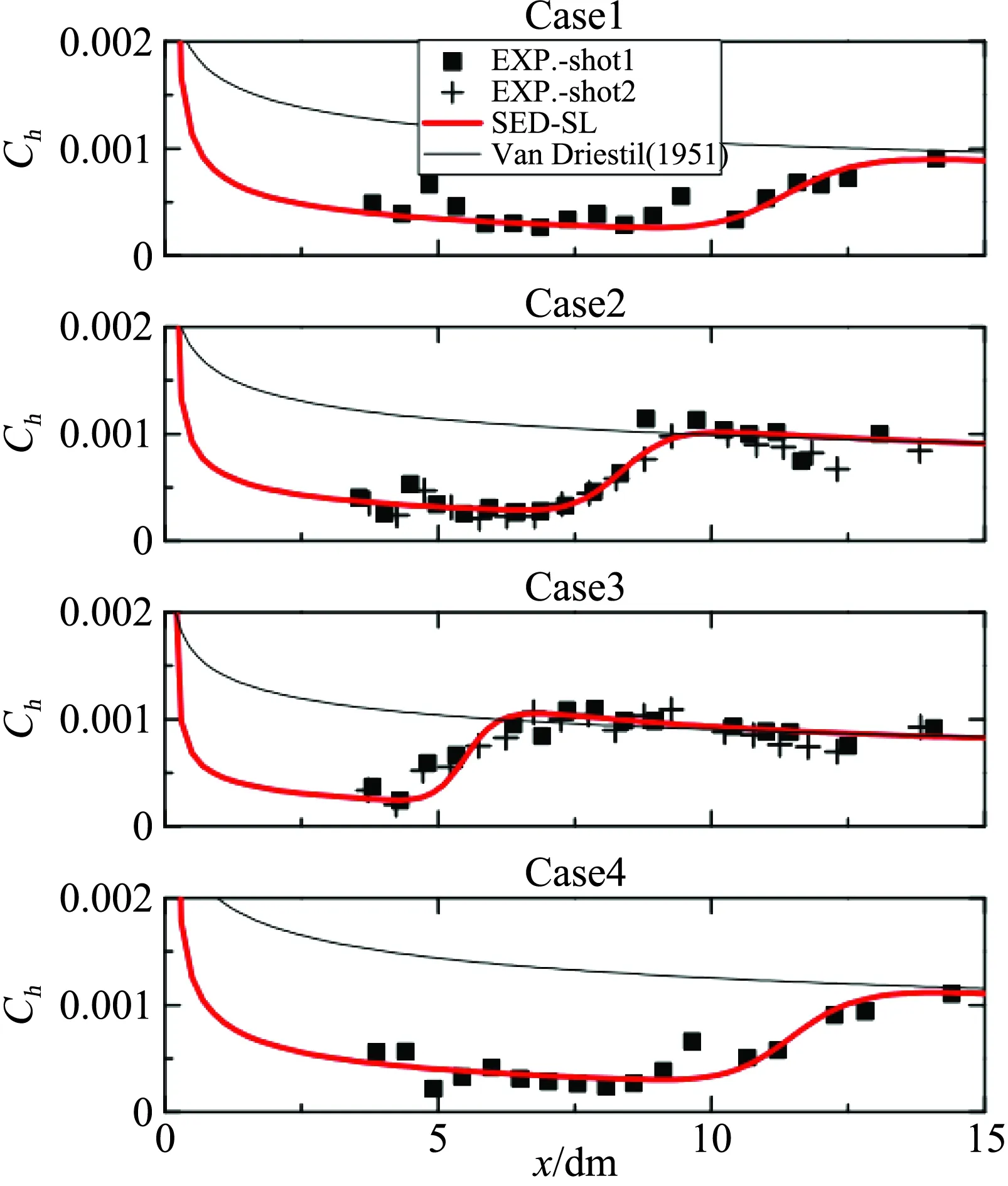
图12 SED-SL模型(实线)对冷壁可压缩边界层不同雷诺数下壁面热流的预测结果符号为实验数据[50]; 红线为SED-SL模型的预测结果Fig.12 Prediction of Stanton number for compressible transitional flat plate flow under cold wall boundary conditionThe black symbols are experimental measurements [50]; the red lines are from SED-SL model

CaseReT0/KT∞/KTwall/KA2.03×107519.2663.32306.36B1.77×107519.2663.32306.36C1.41×107505.3761.63298.16D1.05×107505.3761.63298.16E9.19×106505.3761.63298.16F9.19×106449.8254.86265.39G7.22×106505.3761.63298.16H3.61×106491.4859.94289.97

对未来展望，即使在稀薄气体中，壁面约束产生的对称性约束依然存在，因此，依然可以用序函数分析方法进行验证。但是，对于复杂效应的出现，会出现新的对称破缺，需要添加新的预设，考察多层结构在不同维度(不同统计量)上的表现。这一设想需要通过数据来进行验证。

针对超高空飞行器实验数据难以获取这一难题，值得指出，结构系综理论所实现的最主要的成功在于Re数的相似解。因此，从实验室测量结果向实际飞行结果进行外推，是结构系综理论的一个最主要的应用。未来，我们将针对相关工况，在刻画壁面约束下的能量输运过程中，依据序函数给出的定量预测，给出雷诺数、马赫数变化的预测。

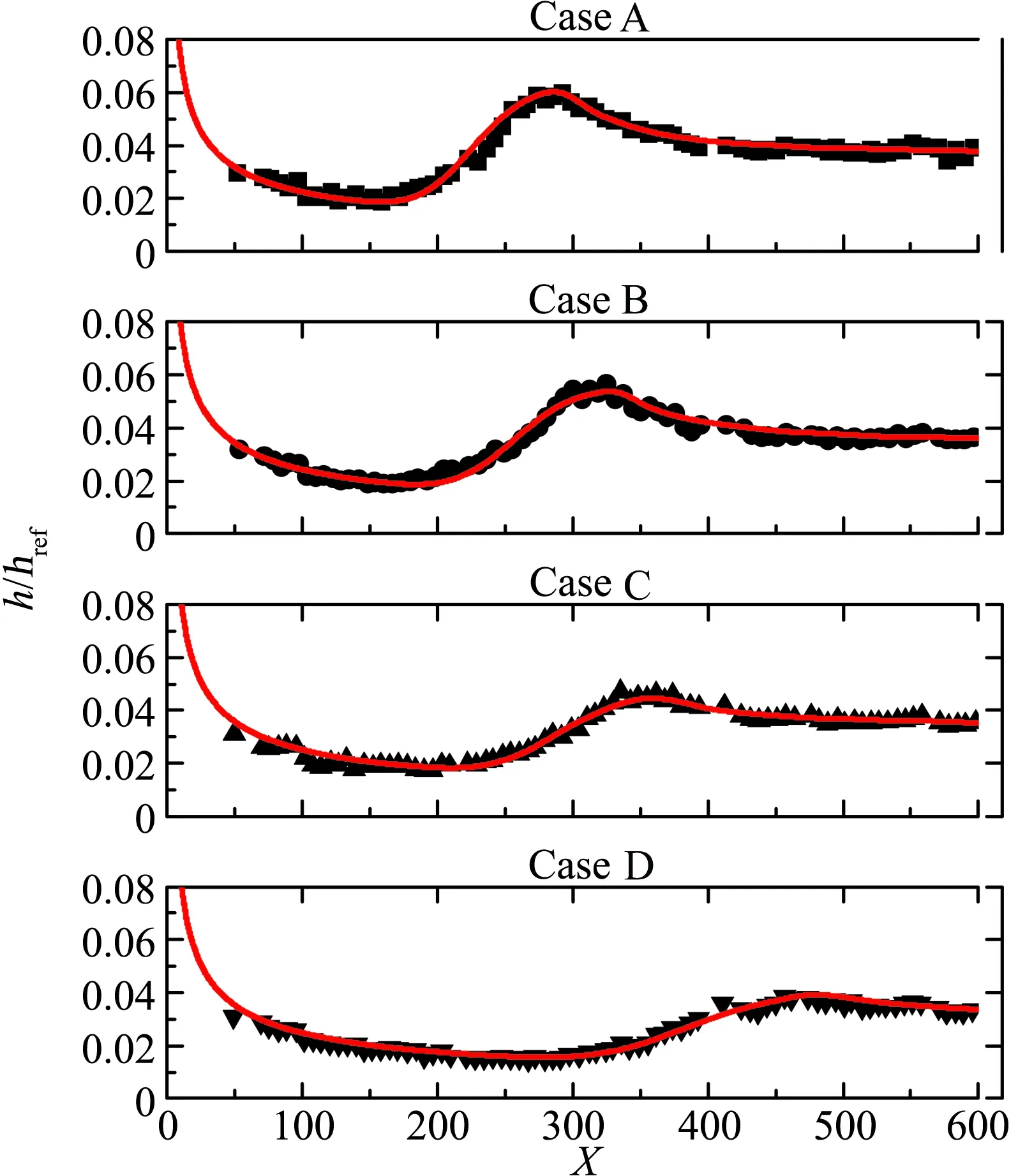
图13 SED-SL模型(实线)对超声速尖锥流动壁面热流的预测结果。符号为实验数据[50]; 红线为SED-SL模型的计算结果Fig.13 Prediction of wall heat flux for transitional supersonic straight cone flow. The black symbols are experimental measurements [50]; the red lines are from SED-SL model

3.4 关于流动控制机理的研究

当前流动控制与湍流结构研究密切相关，近年来随着计算实验技术的进步，对于壁面涡结构的产生、演化从定性上有了丰富的认识，认识到马蹄涡、条带涡结构、大尺度相干结构等多种湍流结构，这些相干结构被认为是时间和空间上稳定的，与边界层质量、动量、热量的输运密切相关。但是尽管大多数人都认同相干结构对于理解壁湍流极为重要，但是对相干结构究竟是什么，以及其在流动中所扮演的角色依然存在着争议[12]。

3.5 关于CFD技术发展

目前，CFD的发展距离高精度、高效率、高可靠性的理想依然有一定差距，其原因在于CFD理论的湍流数学模型部分基础依然薄弱[3]。近年来，我国学者在CFD计算的网格和算法技术上已经有了丰富的积累研究[54]，主要瓶颈还是集中在湍流模型上，此时，可靠的解析解的存在对于CFD的验证起着特别重要的作用。尤其在涉及大分离和转捩等流动的计算时。主流意见认为，RANS方法不可能正确模拟分离，因此，国际学术界趋向于研究LES或者DES等非定常的混合算法。但是建立在空间滤波基础上的LES，与建立在时间平均基础上的RANS计算，其混合尚处于经验的范围[55]。我们认为，建立在对湍流边界层深刻认识基础上的RANS研究仍然有广阔的前景。随着对规范壁湍流认识的推进，人们一定会从基础研究层次上加深对于湍流边界层分离的物理机理的理解，从而使工程湍流模型对分离的预测更加精准。

即使对于LES或混合算法，高效的计算依然依靠对复杂流动中的壁函数的认识[3]，因此，结构系综理论对壁函数的精确刻画会对LES和DES等混合算法的研究起到重要的作用。这也将成为今后一个阶段的重要研究课题。

4 结 论

近年来，随着计算和测量技术的进步，湍流研究已经积累了大量的数据。由于理论上一直没有实质性的突破，导致在湍流模型的开发中，还是一直停留在对已有模型的修补上。大量的修补使得工程应用的湍流模型变得越来越复杂、也越来越难以控制模拟效果。针对这样尴尬的研究现况，必须下大力气，寻求根本性的突破。本文报告了结构系综理论在实现这一突破上已经产生的可喜进步。

湍流理论的突破，以能够充分挖掘大量数据背后的普适规律为标志。一个好的理论不仅能够描述一种流动，而是要能够描述一系列工况下的流动，尤其是要能够比较容易地将一类型流动的规律向其他流动进行推广。结构系综理论已经初步实现了这一目标，它建立的规律顺利地从圆管和槽道流动推广到边界层流动，并从低速推广到高速流动，以及从光滑壁流动到粗糙面(乃至大气)的流动。这些流动都拥有普适的多层结构，只是多层结构参数随流动的不同而呈现有规律的变化。一旦从经验数据中确定了这些参数的变化规律，它将立刻形成一个对于相关流动的精确刻画。

于是，从具体流动的经验数据中验证对称性原理的有效性和提取多层结构参数，就成为结构系综理论应用于未来湍流研究的一个主要内容。值得指出的是，这正是一个成熟理论的标志，即具有将一个规律呈现在人们面前的同时(即验证原理)，还有相应的数据分析方法(即提取参数)，能够从数据中挖掘规律，并指导工程模型的建立。从这一点上来说，结构系综理论实现了一个理论上的重大突破。

于是，从结构系综理论出发所产生的湍流模型，具有传统湍流模型所不具备的一个特点，即参数具备明确的物理意义。因此，在与实验数据的对比过程中，一旦一些参数进行了调整，人们立刻清楚地认识到湍流边界层的物理变化(例如拟涡层厚度的变化)，甚至可以追溯到流动的哪些物理要素出现了变化。这一知识正是在应用中所急需的，因为有了这样的框架，工程师便可以大胆地对未知流动开展参数调节的试验，从而有针对性的对湍流模型进行细致而准确的调整。目前，结构系综理论只是针对有限的一些标准模型进行了参数确定和验证，相信在未来一段时间内，随着更多研究者的参与，它会在大量复杂流动的计算中得到验证和推广，从而建立起从规范流动到工程标模(翼形、压缩拐角等)，再到实际工程复杂流动的一条龙的多层结构演变图，从而实现各类复杂流动的精确预测。特别需要指出的是，在这一过程中，不但工程流动的预测会变得非常准确(直抵实验测量的极限精度)，还会带来工程边界层流动的物理信息。这些信息的日积月累，将为湍流研究提供一个不断扩展的知识和数据库，从而有希望回答诸如决定转捩点位置的关键因素是什么，有多个壁面存在下的流动特性等关键的问题。

复杂系统研究的方法论注重经验研究与理论研究之间的互相衔接和迭代。序函数概念的诞生，产生了一个由实验/计算数据出发，通过计算序函数来系统分析湍流结构效应的研究平台。这一平台填补了一个长期缺失的空白，即在定性的物理机理研究与定量的工程湍流模型研究之间的空白，这一空白的填补使得数值模拟基础研究的大量知识可以用于提升工程湍流模型的质量。总之，只要有(DNS或LES或实验)数据，序函数分析方法就能够进行多层结构的定量刻画，给出精确的参数化方案，从参数的变化当中，可以提取流动结构的变化，这些物理机制的认识，最终可以应用到湍流模型的设置当中。这将迎来工程湍流研究的新阶段。

为什么结构系综理论能够实现研究方法上的突破？在于结构系综理论抓住了壁湍流运动中物理结构的生成法则——即某种广义拉伸不变性所描述的对称破缺是湍流结构生成过程中的宏观体现。今天，高分辨率的数值计算给出了整个流场的所有细节，为我们寻找或验证这样的广义拉伸不变性提供了良好的条件。但是，这里所说的生成法则(即广义拉伸对称性所对应的对称破缺)是隐藏在湍流随机场中的有序物理结构背后的，是在系综层面上的。过去，关于湍流级窜过程的经典描述，也属于这一类的生成法则，在描述均匀各向同性湍流的耗散过程时受到理论家的关注。而贴近流体物理的拟序结构研究，虽然增进了人们对湍流物理机制的形象理解，却忽略了背后的湍流系综的生成法则的探讨[15]，因而并没有产生对应用研究有极大推动意义的定量结果。

结构系综理论所揭示的是普适的对称破缺原理(或生成法则)，这是关于湍流脉动场与平均场背后公共的物理机制，也就是对称性约束的意义。对称破缺决定了湍流平均场的行为，也同时约束了湍流脉动结构。以往关于湍流RANS方程的对称性研究，将相似变量锁定在平均速度上，所以长期未能得到有益的结果。结构系综理论定义的相似变量是长度序函数，是由平均场(平均剪切)与脉动场(雷诺应力)共同决定的。这一序函数物理上刻画了湍流涡结构的尺度，数学上成为定义广义李群拉伸不变量的关键相似变量。这样的理论设置抓住了湍流运动的物理本质，从而方便有效并完整地刻画了壁湍流中真实存在的物理结构-多层结构。

值得指出的是，多层结构是壁湍流的本质性结构，它把普适性和个性、简单性与复杂性进行了有机的统一。任何固壁附近的湍流都拥有形式普适的多层结构，但不同物理条件下的多层结构在定量上略有变化；对于更加复杂的非平衡流动，多层结构参数可以表现出空间或时间上的缓慢变化。于是，结构系综理论创建了可以应用于各类复杂流动的序函数分析方法，从经验数据中提取多层结构参数在空间的变化，从而形成对于真实复杂工程流动的系统化的建模方法，用于湍流模型的开发。