基于双旋运动弹道修正弹系统建模

柯知非，高 敏，王 毅，程 呈，宋谢恩

(陆军工程大学石家庄校区，河北 石家庄 050003)

0 引言

弹道修正弹是指通过采用弹道修正技术，减小传统弹药的射击散布以及圆概率误差值。弹道修正弹在飞行弹道的恰当弧段上能够根据弹箭偏离预定轨迹或偏离目标的情况，通过使用燃气动力(脉冲的或连续的)或利用空气阻力对弹道做低次数或短时间的修正，从而减少弹道偏差，向固定目标或移动目标靠近，从而较大幅度提高了射击密集度和对目标的命中概率[1]。

当前，基于传统的6自由度的弹道模型，已经很成熟，有许多著作对其进行了系统的论述与研究[1-6]。以上著作中，尽管采用的坐标系、投影方法与描述外弹道的参数方法不完全相同，但基本上是采用牛顿-欧拉(Newton-Euler)法建立的6自由度运动方程。以上模型虽能较好的对普通弹丸进行弹道解算与弹道特性分析，但无法准确描述修正组件与弹体之间的关系。

针对此问题，Gagnon E和Lauzon M等将固定鸭舵产生的力和力矩施加在普通榴弹上，采用6自由度刚体弹道模型对弹丸的运动状态进行描述[7]。该模型虽可应用于弹丸的弹道特性分析，但应用于弹道解算时将会引入不能准确描述弹丸受力的模型误差。Wernert等针对155 mm鸭舵式双旋炮弹进行了开环弹道仿真研究和风动试验[8]，他假设前体组件制动后可完全减旋，在此情况下建立了6自由度运动方程，并通过弹丸攻角对舵偏响应进行了极坐标图分析。该模型在鸭舵的修正能力和稳定性的研究上有一定的意义，但在无控飞行和控制策略的拟定上有所欠缺。

为研究前后体(轴承将弹丸结构分成两部分，分别称为前体和后体)质量比和轴承摩擦力对无控状态下弹丸运动状态的影响，Costello M针对双旋结构弹丸建立了7自由度刚体弹道模型[9]，并对无控状态下的弹道特性进行了研究，指出轴承摩擦力和前后体弹丸的质量比是影响无控状态下弹丸弹道特性的主要因素。该模型中，弹丸的前体和后体为较为一般的概念，即轴承的安装位置及弹丸前后体的运动状态并不确定，虽具有无控状态下双旋结构弹丸弹道特性的一般规律，但由于其不能有针对性地描述弹丸的运动状态，不能作为二维弹道修正弹用于弹道解算的弹道模型。Wernert P、Theodoulis S等针对ISL正研发的CCF弹道修正引信建立了7自由度刚体弹道模型[10]。然而在建模过程中，仅在普通榴弹的刚体弹道模型基础上添加了描述鸭舵滚转状态的动力学和运动学方程，未讨论鸭舵和弹体间的相互作用。

针对以上问题，本文在前人研究的基础之上，通过分析修正组件与弹体之间的运动特点，建立其运动约束关系，选择适宜的坐标系，利用多刚体理论建立起完整的适用于多种型号的修正弹弹道模型。

1 飞行原理

弹道修正弹所搭载的二维修正组件，是在传统引信的基础上增加弹道测量、飞行控制、舵机、电源等，使其内部结构和外形尺寸均发生了较大变化，修正组件结构示意图如图1所示。

弹丸出炮口后，在空气作用下差动舵上形成导转力矩，使修正组件相对于弹体反向旋转。当弹丸飞行至预定区域后，舵机收到飞控系统指令，差动舵增大差动角，在空气阻力的作用下使前体修正组件转速进一步衰减，进而相对地面系静止，而后体弹体几乎不受影响，仍处在较高转速以保持陀螺稳定。同时，同向舵在飞控算法的作用下进行实时舵偏角控制，实现弹道的修正，修正组件外形示意图如图2所示。

图2 二维弹道修正引信外形示意图Fig.2 Contour diagram of 2D trajectory correctionfuze

为建立更为精确的弹道模型,需准确描述修正组件与弹体之间的关系,采用多刚体理论对该型弹丸两部件间的相对运动和相互作用进行分析，建立起描述两者相对运动和相互作用的数学关系。在此基础上，选用适当的坐标系对单独考虑舵片受力的方案进行研究，并建立分别应用于弹道解算和弹道特性分析的多刚体弹道模型。

2 弹道建模

2.1 双旋运动分析

如图1、图2所示，定义修正组件为前体(Forebody，FB)，去掉引信部分的修正弹作为后体(Afterbody，AB),两者之间通过螺纹连接，两者轴线重合(不计安装误差)，则两者轴向运动的角速度相同，但两者绕轴线自转的滚转角速度不同。在不考虑修正组件和弹体间气动耦合的情况下，分别视两者为刚体来研究其运动学关系和相互作用。

2.1.1FB与AB的运动学关系

设弹丸质量、修正组件质量和弹体质量分别为m、mf和ma，本文中所提到的弹体指代的是弹丸去掉引信后的部分(即后体)，且三者质心分别为G、Gf和Ga，则有

(1)

式(1)中，la、lf分别为弹丸质心G到修正组件质心Gf、弹丸质心G到弹体质心Ga的矢量。

设弹丸质心的速度为v，则修正组件质心速度和弹体质心速度分别为：

(2)

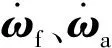
(3)

设弹丸质心的加速度为 ，则修正组件质心加速度和弹体质心加速度分别为：

(4)

综上可得描述修正组件和弹体运动状态的数学表达式。

2.1.2FB与AB的相互作用

无控状态下，修正组件和弹体之间的力和力矩通过轴承传递。有控状态下，则需要添加制动器产生的两者之间的控制力矩，控制力矩方向在弹丸的轴线方向。修正组件所受力和力矩可表示为：

(5)

式(5)中，Ffq、Mfq为修正组件所受的气动力和气动力矩，Ffa、Mfa为弹体对修正组件作用的力和力矩(包含控制力矩)， 为修正组件所受重力。同理，弹体所受力和力矩可表示为：

(6)

式(6)中，Faq、Maq为弹体所受气动力和气动力矩，Faf、Maf为修正组件对弹体作用的力和力矩(包含控制力矩)，mag为弹体所受重力。

综上，可得

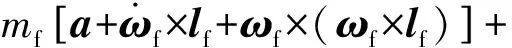
(7)

假定修正组件和弹体之间没有气动耦合，则有

mfaf+maaa=Ff+Fa=
Ffq+Ffa+mfg+Faq+Faf+mag=
(Ffq+Faq)+(mfg+mag)=Fq+mg

(8)

故有

ma=Fq+mg

(9)

由式(5)-式(9)可知，修正组件和弹体的质心运动可统一用弹丸的质心运动来描述。假定修正组件和弹体之间没有气动耦合，弹丸所受气动力为修正组件和弹体所受气动力的矢量和，因此，弹丸质心运动的动力学方程中，弹丸的受力可直接采用所受气动力和重力计算。

由于修正组件和弹体的轴线重合，两者在俯仰和偏航平面内绕各自质心的转动可通过弹丸绕弹丸质心的转动来描述。将两者的旋转中心都移至弹丸质心，分别作用在两者上的气动力合力的作用点与旋转中心的距离改变，造成所形成的力矩幅值改变，使力矩表达式极为复杂。本文中选用的气动参数均以弹丸质心为弹丸的旋转中心，即气动参数中弹丸力矩的计算均以弹丸质心为基点，以弹丸质心作为旋转中心利于弹道建模工作的展开。

2.2 飞行动力学模型

发射系内建立的运动方程组用于弹道解算。首先建立弹丸质心的运动方程组，然后依据修正组件和弹体的绕弹丸质心的转动描述弹丸绕质心转动的方程组，依据两刚体的运动学关系可将所建立的方程简化，建立描述弹丸运动状态的弹道模型。

2.2.1坐标系

本文所使用的坐标系及角度定义见文献[11]，所使用坐标系包括地面坐标系Oxyz、弹体坐标系Ox1y1z1、速度坐标系Ox3y3z3、准弹体坐标系Ox4y4z4、准速度坐标系等Ox5y5z5，发射系与弹丸出炮口瞬间的地面坐标系完全重合，所使用的角度包括俯仰角φ、偏航角ψ、弹道倾角θ、弹道偏角σ、攻角α、侧滑角β等。

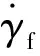
图3 准弹体坐标系下两刚体滚转角Fig.3 Two roll angles in the equal coordinate system of projectile body

2.2.2弹丸受力的分解

修正组件滚转角的定义如图4所示。当操纵舵处于水平位置并产生向上的控制力时，定义固定舵滚转角为0°，产生向下的控制力时为±180°。从弹尾向前看，固定舵向右滚转为正，向左滚转为负。

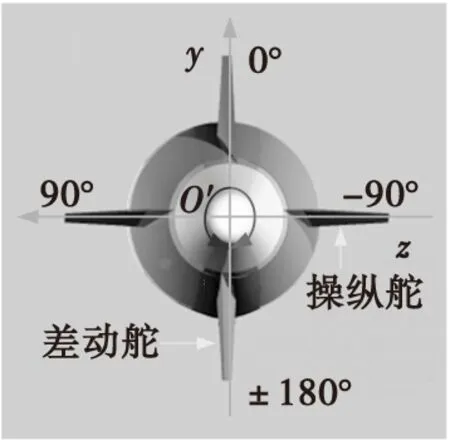
图4 修正组件滚转角定义Fig.4 Definition of the roll angle of correction kit

弹丸整体的气动参数通过网格计算获得，且气动参数为弹体系下的气动参数。由于弹丸气动布局不对称，获取弹丸受力时的气动参数应采用弹体下的攻角α*、侧滑角β*进行插值计算。而攻角α、侧滑角β均定义在准弹体系下，因而应首先找到两组攻角、侧滑角的几何关系。准弹体系下攻角和侧滑角的计算方法如下：

(10)

式(10)中，v为弹丸合速度，vx4、vy4和vz4为弹丸速度矢量在准弹体系上的投影。

准弹体下攻角α、侧滑角β向弹体系攻角α*、侧滑角β*的转换过程如下：

(11)

采用α*、β*和马赫数Ma进行气动插值获得相应的气动参数后，进行弹体系下气动力和气动力矩的计算，而后转换到准弹体系下。准弹体系下弹丸受力如下：

(12)

修正组件和弹体的马格努斯力垂直于总攻角平面，而马格努斯力矩在攻角平面内，分别将其转换到准弹体坐标下，得表达式如下：

(13)

式(13)中，各量分别为修正组件和弹体所受马格努斯力和马格努斯力矩在准弹体下的分量。

2.2.3发射系下运动方程组的建立

飞行过程中，弹丸的运动状态通过弹丸质心的运动和绕质心的转动来描述。将弹丸质心的运动描述在发射系下，即弹丸质心的速度、位置信息均在发射系下投影，利用该方式进行弹道解算，便于与实际飞行状态下的弹丸速度、位置信息相对比，是当前弹道解算的常用方法。将弹丸绕质心的转动建立在准弹体坐标系下，形式最为简单。

建立描述弹丸运动状态的运动方程组如下：

(14)

式(14)中，Mfax4、Mafx4分别为修正组件和弹体间相互作用力矩在准弹体系x4轴上的分量，该力矩包括轴承间的摩擦力矩和制动过程中的控制力矩。

参照滚动轴承摩擦力矩公式(11)可得飞行过程中的摩擦力矩计算如下：

(15)

式(15)中，Mfax4f为作用在修正组件的摩擦力矩，f1为载荷系数，P1为轴承载荷，dm为轴承平均直径，f0为润滑系数，与所采用的润滑方法有关，ϑ为润滑剂粘度系数，sgn为符号函数。

由于大括号中第二项值很小，可忽略，且弹丸飞行过程中两刚体之间始终存在相对运动，则式(15)可整理为：

Mfax4f=f1P1dm

(16)

式(16)中，载荷系数f1和轴承平均直径dm一定，故修正组件与弹体间的摩擦力矩轴承承受的载荷成正比。

无控状态下，无控制力矩。在有控状态下，除摩擦力矩外仍需考虑控制力矩。当固定舵稳定在相对

于地面的某一角度式，修正组件所受气动力矩在x4轴上的投影处于平衡状态，即

(17)

此处可求得作用在弹体上的控制力矩 ，将其带入式(14)中即可进行有控状态下的弹道解算。

2.2.4绕弹丸质心的转动方程组

1)弹丸绕质心转动的动力学方程组

本文不加推导直接给出修正组件绕弹丸质心转动的动力学方程组

(18)

式(18)中，Jfx、Jfy、Jfz为修正组件相对弹丸质心的转动惯量在准弹体上的投影，ωfx4、ωy4、ωz4为修正组件的角速度在其准弹体系上的投影，Mfx4、Mfy4、Mfz4为修正组件所受气动力矩在准弹体上的投影，Mfax4、Mfay4、Mfaz4为弹体对修正组件作用的力矩(包含控制力矩)在准弹体上的投影。

同理，可给出弹体绕其弹丸质心的转动动力学方程组

(19)

式(19)中，Jax、Jay、Jaz为弹体相对弹丸质心的转动惯量在准弹体系上的投影，ωax4、ωy4、ωz4为弹体角速度在其准弹体系上的投影，Max4、May4、Maz4为弹体所受气动力矩在准弹体系上的投影，Mafx4、Mafy4、Mafz4为修正组件对弹体作用的力矩(包含控制力矩)在准弹体上的投影。

将式(18)和式(19)中的后两式分别相加，则有

(20)

式(20)中，弹丸相互作用力矩Mfay4与Mafy4和Mfaz4与Mafz4是弹丸整体的内力。令Jy=Jfy+Jay，Jz=Jfz+Jaz，My4=Mfy4+May4，Mz4=Mfz4+Maz4，My4、Mz4分别为弹丸整体所受气动力矩在准弹体系y4轴、z4轴上的分量，故式(20)可整理为：

(21)

因而，得弹丸绕质心运动的动力学方程组

(22)

2)弹丸绕质心转动的运动学方程组

弹丸姿态使用俯仰角φ、偏航角ψ、修正组件滚转角γf和弹体滚转角γa4个变量来描述。设准弹体坐标系相对于地面发射系的转动角速度为ω′，则有

(23)

弹体坐标系相对于地面坐标系的转动角速度ω可写成

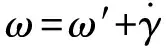
(24)

则有

(25)

整理后，可得

(26)

3 仿真与飞行试验验证

在某实验基地进行某型加装修正组件的榴弹飞行试验，其中，结构弹1发，如图5所示。固定鸭舵舵偏角6°。弹丸采用45°射角发射，炮目连线方向为212.468 8°，射向在炮目连线基础上左修20 mil。弹丸实际初速908.2 m/s，射程28.9 km。

图5 二维修正榴弹Fig.5 2-D correction projectile

由于弹上未安装记录仪，仅能通过雷测曲线进行数据的分析对比，结果如图6—图11所示。

由图6—图9可知，仿真曲线与雷测曲线在合速度、弹道高、x向速度和y向速度上重合度很高，合速度偏差不大于3 m/s，最大弹道高偏差约为40 m，x向速度偏差不大于3 m/s，y向速度偏差不大于2 m/s。图10和图11中，侧偏和z向速度也能较好的与雷测曲线保持一致，侧偏偏差不大于60 m，速度偏差不大于4 m/s。仿真落点与实际落点相比，纵向偏近16 m，横向偏远48 m。仿真结果与实际弹丸落点偏差小于弹丸射程的5‰，其精度满足要求。

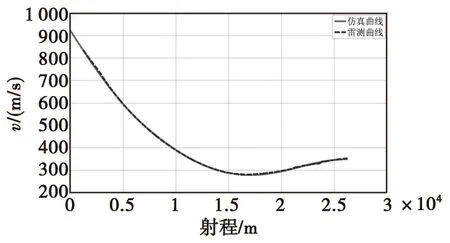
图6 射程合速度曲线Fig.6 Curve of the range-speed

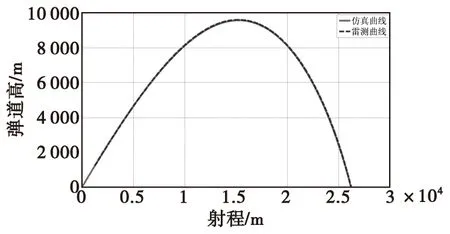
图7 射程弹道高曲线Fig.7 Curve of the range-highth

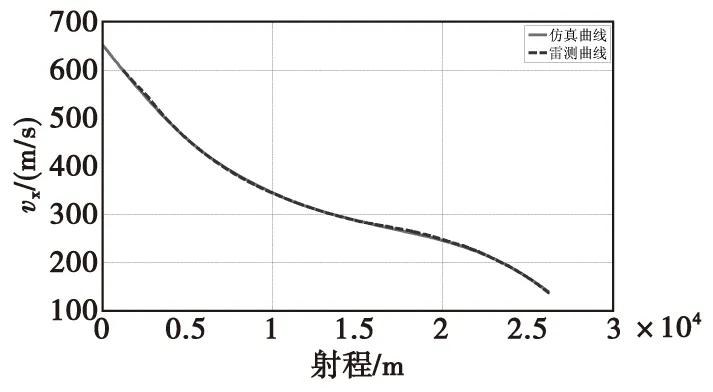
图8 射程x向速度曲线Fig.8 Speed curve of the x direction

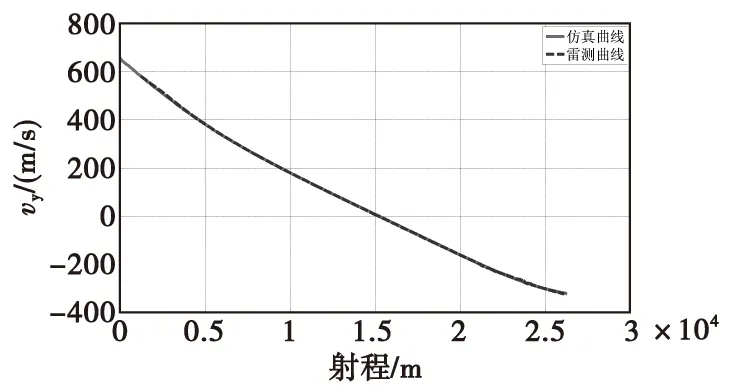
图9 射程y向速度曲线Fig.9 Speed curve of y direction

图10 射程侧偏曲线Fig.10 Cornering curve of the range

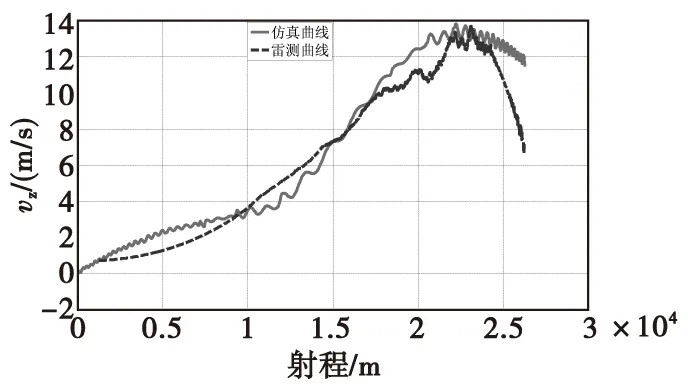
图11 射程z向速度曲线Fig.11 Speed curve of z direction

仿真结果与雷测曲线的对比表明，所建立的数学模型可对修正弹的质心运动状态进行准确描述，验证了模型建立的正确性。

4 结束语

本文在分析修正组件与弹体的双旋运动的基础上，建立了多刚体修正弹弹道模型。仿真和飞行试验结果表明，所建立的数学模型可对弹丸的运动状态进行准确的描述，仿真结果与实际弹丸落点偏差小于弹丸射程的5‰，符合精度要求。但文章并未对双旋运动下的角运动和飞行稳定性情况未进行进一步分析，需要在今后的工作中进一步研究。