一系水平悬挂刚度对高速客车动力学性能的影响研究*

岳 鹏, 李国芳, 丁旺才, 吴 丹, 李 昕

(1 兰州交通大学 机电工程学院， 兰州 730070；2 兰州交通大学 艺术设计学院， 兰州 730070)

随着高速车辆的快速发展，人们对车辆的速度和舒适度提出了更高的要求。铁道车辆系统中，悬挂系统是影响其动力学性能的关键因素[1]。悬挂参数的合理设计对提高车辆系统动力学性能具有十分重要的作用，良好的动力学性能使得车辆在通过曲线时，轮轨作用力足够小从而减轻车轮与钢轨间的磨耗，减少线路维护工作，节约能源。因此，研究悬挂参数对车辆系统动力学性能的影响具有十分重要的现实意义。

研究基于车辆-轨道耦合理论，建立某型客车车辆动力学模型，考虑其中的非线性因素，计算得出了不同一系横、纵向刚度参数下，车辆系统的动力学性能响应，分析了一系横、纵向刚度参数对车辆动力学性能的影响，从而为车辆系统一系横、纵向刚度参数的标准制定提供理论依据。

1 高速客车动力学模型的建立

1.1 建立模型

文中建立了具有50个自由度的某型高速客车车辆动力学模型，由1个车体、2个构架、8个轴箱、4个轮对共计15个刚体组成。车辆动力学模型的主要参数见表1，自由度见表2，车辆动力学模型见图1。

1.2 模型中考虑的非线性环节

(1)非线性轮轨接触几何关系

车辆动力学模型采用LMA型踏面与CN60轨相匹配的轮轨接触几何关系，轮轨接触几何参数认为是轮对横移量的非线性函数。

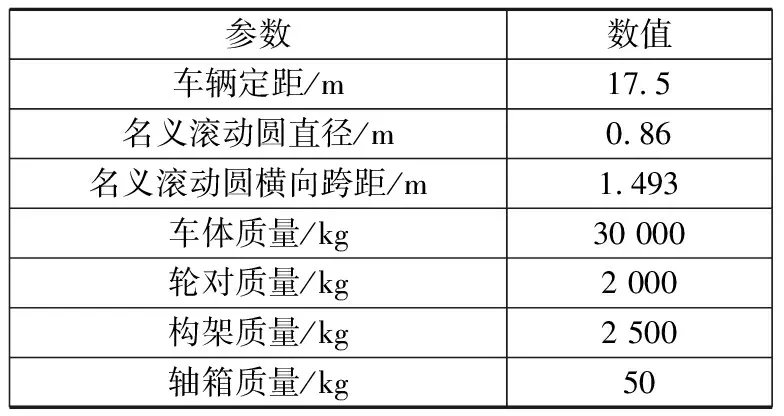
表1 车辆动力学模型主要参数

表2 车辆动力学模型的自由度

图1 某型高速客车动力学模型

(2)非线性轮轨相互作用力

轮轨间的蠕滑力由Kalker非线性蠕滑理论计算，然后可通过迭代计算得到钢轨作用于轮对上的横向力和摇头力矩。

(3)非线性悬挂力

非线性悬挂力包括各种间隙、止挡、横向和垂向减振器、空气弹簧、空气弹簧失气时的摩擦特性等。

1.3 动力学方程

在以下算式中，轮对相对于轨道中心线的横向位移y和轮对的摇头φ，轴重为P，踏面斜率为λ，滚动圆半径为r0，滚动圆间距之半为s，r为蠕滑率。根据定义，作用在左右车轮踏面上纵向蠕滑力分别为FxL、FxR，横向蠕滑力分别为FyL、FyR，自旋蠕滑力矩分别为MzL、MzR，表达式如式(1)

(1)

其中

(2)

由此可得横向上轮对轮轨力表达式为：

(3)

其中Pλ/s为重力刚度。轮对在摇头方向上摇头力矩表达式为：

(4)

由此可得轮对考虑惯性力、悬挂力和轮轨作用力的动力学方程为：

(5)

上式中f22和f23很小，可忽略不计，式(5)可以简化为：

(6)

分离式(6)中的轮轨接触参数项与悬挂参数项，由此可得：

(7)

式中

根据一系悬挂纵向刚度Kx、横向刚度Ky的变化来分析对高速车辆系统动力学性能的影响。

2 横向运行稳定性

车辆系统在轨道上运行时，车辆与轨道构成复杂的动力学系统，当车辆运行速度达到一定值时，系统会发生蛇行失稳，系统的振动幅度明显增大，动力学性能也明显恶化，大大增加了车辆脱轨的可能，因此，车辆系统的非线性临界速度是判断车辆是否失稳的重要指标[2]。

给车辆系统一个初始激励，让其在刚性直线无不平顺轨道上运行，根据系统的响应不再收敛于平衡位置而是趋于稳定的极限环来确定临界速度[3]。

图2、图3是一系悬挂纵向和横向刚度分别为Kpx=1.2 MN/m、Kpy=0.9 MN/m下，当速度为449 km/h及以下时，车辆系统1位轮对的时间历程图如图2(a)所示，图3(a)为所对应相平面图；当速度达到450 km/h时，车辆系统1位轮对的时间历程图如图2(b)所示，图3(b)为所对应相平面图；图中所示的相平面图都除去了1位轮对在轨道初始激励的响应。速度为449 km/h及以下时，1位轮对的横向位移随着时间的增加，逐渐收敛于平衡位置见图2(a)，相轨迹收敛于极限环的奇点见图3(a)。当速度增加到450 km/h时，1位轮对的横向位移随着时间的增加，不会收敛于平衡位置而是做等幅的周期运动见图2(b)，相轨迹趋于稳定的极限环见图3(b)，由此可得车辆系统的非线性临界速度为450 km/h。根据上述方法，可以得到一系横、纵向刚度参数对车辆系统非线性临界速度的影响如图4所示。

图2 轮对横向运动时间历程图

图3 轮对横向运动相平图

由图4可以得出，车辆系统的非线性临界速度随着一系悬挂纵向刚度Kpx及横向刚度Kpy的增大呈线性增大，由此可以得出在低刚度的范围内，提高一系悬挂刚度能增大车辆系统的临界速度。当Kpx=1.8 MN/m，Kpy=1.5 MN/m时，车辆系统非线性临界速度达到了465 km/h。

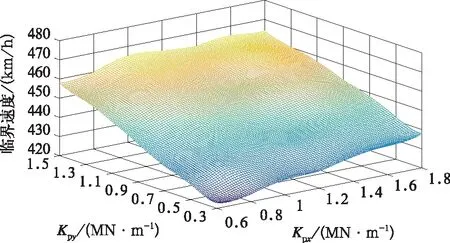
图4 一系横、纵向刚度对 非线性临界速度的影响

3 曲线通过性能

为了研究车辆系统以一定的速度通过曲线轨道时的脱轨系数、轮重减载率、轮轴横向力等曲线通过性能指标变化情况，以上动力学性能指标都选取高速车辆系统的1、3位轮对的左侧车轮为研究对象，现设置曲线轨道参数如表3所示。

表3 曲线参数设置 m

根据我国相关文献[7-8]规定，对于运行速度200 km/h及以上的高速客车动力学性能指标有如表4所示的执行标准。

高速车辆动力学模型以200 km/h的速度通过上述曲线半径为4 500 m的轨道，轨道上以德国高干扰UIC-good为轨道激励输入，一系悬挂纵向及横向刚度对高速车辆轮对的脱轨系数、轮重减载率及轮轴横向力的影响如图5～图7所示。

表4 我国高速客车动力学性能指标执行标准

由图5可以看出，当车辆系统以200 km/h的速度通过半径为4 500 m的曲线轨道时，因为不同的车轮所处运行状态不完全一致，所以在同一时刻各轮的脱轨系数数值不相符，但总体趋势大概一致，1位、3位轮对的脱轨系数随着一系悬挂横、纵向刚度的增大总体呈现出增大趋势，当Kpx=1.8 MN/m，Kpy=1.5 MN/m时，1位、3位轮对的脱轨系数达到了最大值，分别为0.157和0.133，符合安全限定值。

对车辆系统的曲线通过能力进行评价时，除了脱轨系数还应考虑车轮的轮重减载率等指标，1位、3位轮对的轮重减载率如图6所示，随着一系悬挂横、纵向刚度的增大总体呈现增大趋势，横向刚度较纵向刚度对轮重减载率影响较大，在Kpx=1.8 MN/m，Kpy=1.5 MN/m时，1位、3位轮对的轮重减载率达到最大值为0.568和0.474。总体而言，一系悬挂参数在上述范围内变化时仍低于我国对轮重减载率的安全限定值0.6。

1位、3位轮对的轮轴横向力如图7所示，1位轮对的轮轴横向力主要受一系悬挂横向刚度的影响且其轮轴横向力随着纵向刚度的增大而线性增大；3位轮对的轮轴横向力主要受一系悬挂横向刚度的影响且其轮轴横向力随着纵向刚度的增大而线性增大；当Kpx=1.8 MN/m，Kpy分别为0.3 MN/m和1.5 MN/m时，1位、3位轮对的轮轴横向力达到了最大值分别为11 476.6 N和11 091.2 N。在同一参数下，1位轮对较3位轮对的脱轨系数、轮重减载率和轮轴横向力高。

当高速车辆动力学模型以30 km/h的速度通过上述曲线半径为300 m的轨道，轨道激励为德国高干扰UIC-good不变，一系悬挂横、纵向刚度对车辆动力学模型的脱轨系数、轮重减载率及轮轴横向力的影响如图8～图10所示。

图5 一系横、纵向刚度对脱轨系数的影响(R4 500 m)

图6 一系横、纵向刚度对轮重减载率的影响(R4 500 m)

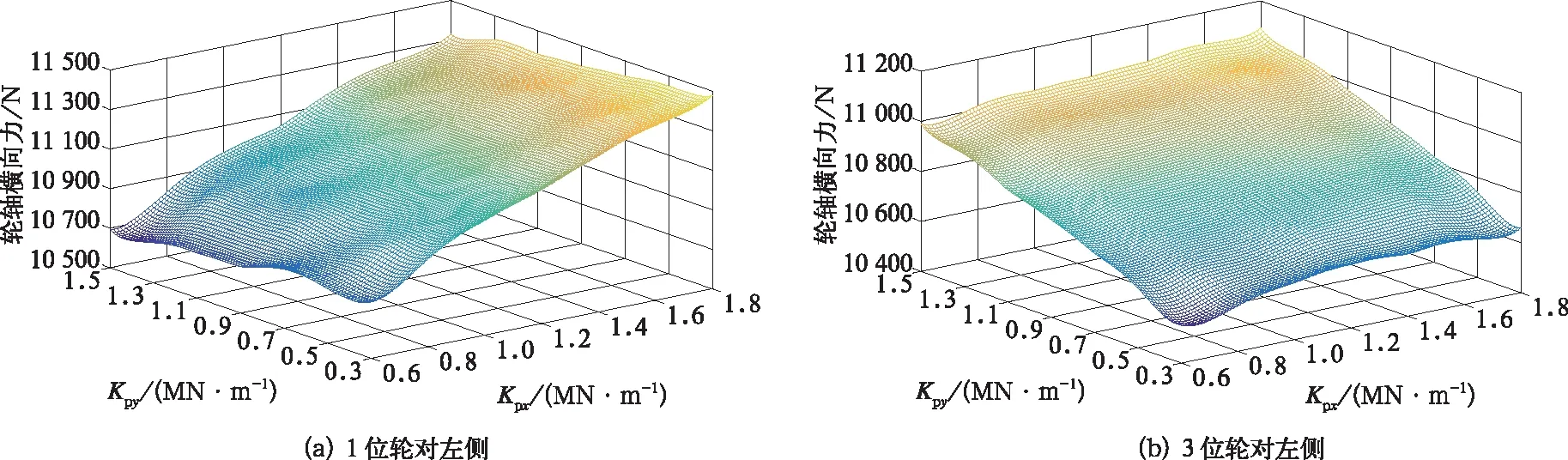
图7 一系横、纵向刚度对轮轴横向力的影响(R4 500 m)

通过图8～图10可以发现，当车辆系统低速通过小曲线半径时，车辆系统的脱轨系数、轮重减载率主要受一系纵向刚度的影响，且1位轮对的脱轨系数、轮重减载率随着一系纵向刚度的增大而增加，当Kpx=1.8 MN/m，Kpy=1.5 MN/m时，1位、3位脱轨系数达到最大值，分别为0.434、0.314，当Kpx=1.8 MN/m，Kpy分别为1.1 MN/m和1.3 MN/m时，1位、3位轮对的轮重减载率分别达到最大值为0.292和0.282，而其轮轴横向力主要受一系横向刚度的影响且随着一系横向刚度的增大而增加，当Kpx=0.6 MN/m，Kpy=1.5 MN/m，1位、3位轮对的轮轴横向力分别达到最大值为12 339.73 N和12 366.57 N。

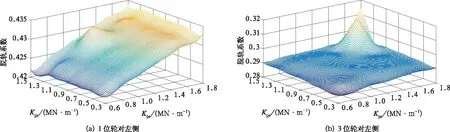
图8 一系横、纵向刚度对脱轨系数的影响(R300 m)

图9 一系横纵刚度对轮重减载率的影响(R300 m)

图10 一系横、纵向刚度对轮轴横向力的影响(R300 m)

比较上述两种曲线半径工况下的动力学性能指标可以看出，车辆系统高速通过大曲线半径工况时，脱轨系数随着一系横、纵向刚度的增大而增大，轮重减载率主要受一系横向刚度的影响且其随着一系横向刚度的增大而增大；当车辆系统低速通过小曲线半径工况时，脱轨系数随着一系纵向刚度的增大而增大，轮轴横向力随着一系横向刚度的增大而增大，轮重减载率受一系横、纵向刚度的影响与大曲线半径轨道下的影响基本一致。

分析上述图5～图10可以得出，当一系横向、纵向刚度值选取较大时，轮对的脱轨系数、轮重减载率和轮轴横向力都呈现出了较大的值，这对车辆系统曲线通过的安全性提出了较高的要求。但上述参数也不能选取较小，因为较小的刚度对车辆系统的减振作用不太明显，从而降低车辆系统的平稳性及舒适度。

4 运行平稳性

高速车辆系统在通过曲线轨道时，除了要满足上述安全性能的要求，也应该要符合平稳性的要求。为了研究在不同的一系横、纵向刚度参数下，车辆系统以一定的速度通过曲线轨道时对平稳性指标的影响，故选距转向架中心一侧1 000 mm的车体底面上的一点为研究对象，让车辆系统通过上述大曲线半径工况，由此可以得到一系横、纵向刚度参数对平稳性的影响如图11、图12所示。

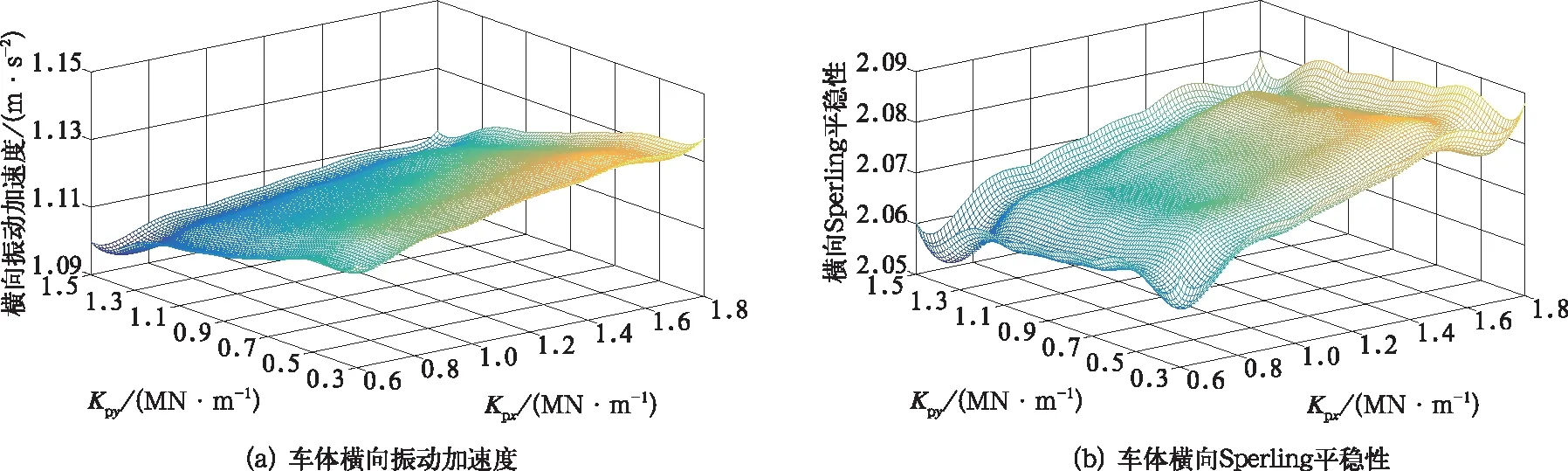
图11 一系横、纵向刚度对车体横向平稳性的影响

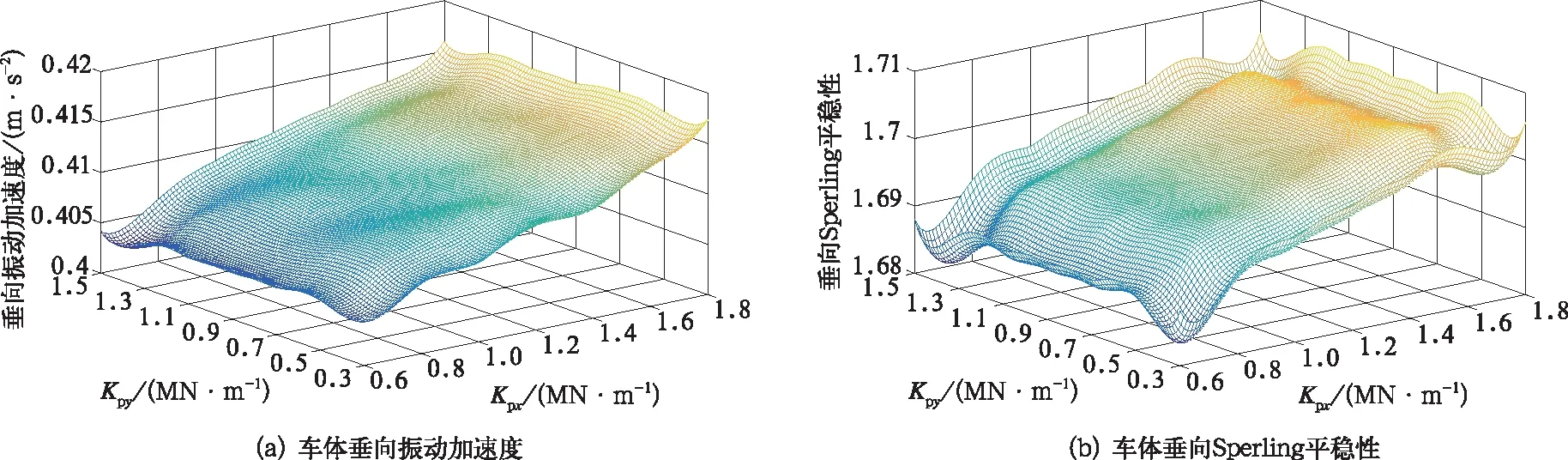
图12 一系横、纵向刚度对车体垂向平稳性的影响

由图11可以看出，车体横向加速度和横向Sperling平稳性指数随着一系悬挂纵向刚度的增大、横向刚度的减小总体呈增大趋势。都在Kpx=1.8 MN/m，Kpy=0.3 MN/m时，出现了最大值分别为1.137和2.088。由图12可以看出，车体垂向加速度和垂向Sperling平稳性指数随着一系悬挂纵向刚度的增大基本呈线性增长，而一系悬挂横向刚度对车体垂向上的平稳性没有太大的影响。当Kpx=1.8 MN/m，Kpy=1.5 MN/m时，车体横向加速度和横向Sperling平稳性指数都达到了最大值，分别为0.417和1.706。

比较图11、图12可以得出，当一系悬挂横向刚度参数较小、纵向刚度参数较大时，车体的横向平稳性指数较大，而当一系悬挂横、纵向刚度参数都较大时，车体的垂向平稳性指数较大。

5 结 论

利用多体动力学软件UM建立了某型高速客车动力学模型，研究分析了车辆系统通过曲线轨道时，不同的一系悬挂横、纵向刚度参数对车辆系统的横向运行稳定性、曲线通过性能及平稳性的影响，结论如下：

(1)车辆系统非线性临界速度随一系悬挂横、纵向刚度参数的增大而线性增加。

(2)当一系悬挂横、纵向刚度参数选取较大时，轮对的脱轨系数、轮重减载率和轮轴横向力都呈现出了较大的值，这对车辆系统曲线通过的安全性提出了较高的要求。

(3)当一系悬挂横向刚度参数较小、纵向刚度参数较大时，车体的横向平稳性指数较大，而当两者参数都较大时，车体的垂向平稳性指数较大。

综上，设计一系悬挂横、纵向刚度参数时，须进行参数优化以得到最优值，建议一系悬挂横向刚度值为0.7～1.1 MN/m，一系悬挂纵向刚度值为1～1.4 MN/m，这样既能满足车辆系统良好的稳定性及曲线通过性能，又能保证车辆系统具有良好的平稳性。