基于代价敏感性和概率校准的先天性心脏病概率预测模型研究*

罗艳虹 李 治 余红梅 郭虎生 曹红艳 王 蕾 宋春英 郭兴萍△ 张岩波△

我国是先心病高发国家,2010-2011年我国活产新生儿先心病的发生率高于其他类型出生缺陷[1]。遗传因素、母亲孕期患病及用药等因素都会导致子代先心病的发生,因此早期预测子代先心病的发病风险,尽可能消除各种可能的危险因素,对预防先心病起关键作用。利用山西省先心病数据,采用机器学习算法,建立预测性能优良的预测模型,可为筛选先心病高危人群提供参考依据。国内外基于影响因素对出生缺陷的预测研究较多,但大多数研究关注分类预测[2-5],很少有研究针对先心病进行概率预测,故本文研究先心病的风险概率预测。对于全部出生儿的调查数据进行先心病概率预测时,先心病发生与否的两种类别存在比例不平衡,机器学习算法通常针对类别平衡数据,因此,对于不平衡数据,机器学习算法对于多数类易产生“过拟合”,导致预测概率有偏差,降低预测性能[6-8]。

针对不平衡数据的处理方法大致分两种:一种是改变训练样本分布,可以采用随机抽样以增加少数类样本或减少多数类样本降低数据的不平衡性[9]；另一种通过改进算法补偿数据的不平衡性,如代价敏感性学习。综上所述,利用不平衡数据构建模型进行概率预测时,先心病预测概率有可能存在偏差,对此可以采用代价敏感性学习和概率校准的方法进行“纠正”,提高模型的概率预测性能。

概率校准(probability calibration)就是采用函数把原始模型的分类或概率转换为准确的概率[10]。一个良好校准的预测模型可以反映疾病发生的潜在概率。常用的概率校准方法是Platt scaling和Isotonic regression[11-12]。众多研究表明,经过Platt scaling校准的支持向量机(support vector machines,SVM)、随机森林(random forest,RF)和boosted tree的预测概率最准确,其中boosted tree不仅训练时间长而且需要的存储量大,所以首选SVM和RF模型[13-14]。因此,选取SVM、RF及应用广泛的logistic回归模型作为本文的概率预测模型。logistic回归的预测概率不产生偏倚,校准效果不明显[14]。

资料与方法

1.研究资料

根据山西省各县、市的生态环境、地理位置、医疗条件和经济状况等因素,本文的研究对象选自山西省6个县(市)(中阳县、代县、平定县、怀仁县、交口县和汾阳市)在2006-2008年出生的所有健康新生儿及先心病患儿的母亲或父亲,通过让研究对象填写出生情况调查表获取调查数据。先心病的确诊以先前医生的诊断为准;先心病疑似病例请先心病专家确诊。

通过对调查数据进行初步分析发现,涉及的多数危险因素如母亲孕期患病和母亲既往病史等因素的发生率很低,直接引入方程,影响预测效果,故对变量进行初步分析,本文生成9个综合变量,其中综合变量的值为包含的各个危险因素的值相加得到[15-16]。综合变量包含的危险因素见表1。

2.加权支持向量机和加权随机森林

(1)加权支持向量机

支持向量机利用核函数采用非线性映射将线性不可分的原始数据投影到高维空间,使原始数据在高维空间线性可分。常用的核函数有线性核、径向基核和多项式核等。本文通过测试确定SVM的核函数为线性核。当SVM处理的数据存在类别不平衡时,可以采用Veropoulos等提出的代价敏感性算法,将多数类和少数类样本的惩罚系数之比定为二者例数的倒数,该法是SVM分析非平衡数据的常用方法[17]。本文采用该法,构建WSVM。

(2)加权随机森林

RF对原始样本进行多次bootstrap重抽样产生多个样本,每个样本的样本量和原始样本相同,对所有样本构建决策树,且决策树在生长过程中不剪枝,最终的预测结果通过对多棵决策树的预测结果进行多数投票产生[18-19]。对于本文的先心病不平衡数据,为了保留原有数据结构,本文基于代价敏感性思想,构建WRF。根据相关文献建议,小类的权重设定为2或3,本研究经过对比选择权重为2[20]。

表1 9个综合变量的描述

RF有三个主要参数:一是构成RF的决策树棵数ntree;二是树节点处预选的变量数mtry;三是叶节点nodesize的大小。经过对比,这些参数的取值分别设定为ntree=500,mtry=3,nodesize=65,cutoff=c(0.7,0.3)。

对于预测模型,需要从原数据中进行重抽样生成训练集和测试集。对于本文的极端不平衡数据,采用分层bootstrap重抽样,即从少数类和多数类样本中分别随机抽取三分之二构成训练集,剩余的样本构成测试集。本文采用三折交叉验证及网格搜索(grid search)选取WSVM和WRF的参数。由于随机抽样会使构建的模型结果存在多变性,故抽样及构建模型过程重复1000次。本文所有程序均采用R软件实现。

3.概率校准

两种常用的概率校准方法为Platt scaling校准和Isotonic regression校准。当模型的预测值产生S形扭曲,采用Platt scaling校准。Isotonic regression校准属于非参数校准,采用pair-adjacent violators(PAV)算法[21-22]。

(1)Platt校准

针对模型的预测结果f(x),由(1)式sigmoid函数产生校准概率:

(1)

其中,f=f(x),采用最大似然估计得到参数A和B的取值[11]。

(2)Isotonic校准

保序回归的公式如下:

yi=m(fi)+εi

(2)

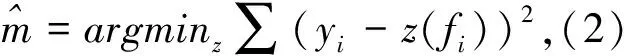
4.预测模型的评价

常用的概率预测评价指标有AUC和RMSE。AUC的取值较高,RMSE的取值较低时,模型的预测精度较高。任何模型都不可能在所有的评价指标上取值都理想。当模型合适的评价指标未知时,SAR是一个稳健的评价指标,SAR=(ACC+AUC+(1 -RMSE))/3[23-24],其中ACC为Accuracy的简称。选用AUC、RMSE和SAR作为本文模型的评价指标。

结 果

1.综合因素描述

本文调查总人数为33831人,其中健康新生儿33753例,先心病患儿78例。综合变量的描述见表1。

2.各个模型Platt校准和Iso校准效果比较

由于篇幅所限,本文结果仅针对测试集。表2给出重复抽样1000次,6个模型评价指标的中位数、上四分位数P25和下四分位数P75,其中WSVM-Platt、WSVM-Iso分别代表基于Platt校准和Isotonic校准的WSVM模型。WRF-Platt和WRF-Iso分别代表基于Platt校准和Iso校准的WRF模型。

由表2可得,logistic模型的AUC和SAR值的中位数分别高于0.83和0.92;AUC值的P25和P75都高于0.8,SAR值的P25和P75都高于0.9。

表2 测试集6种模型预测结果的比较(Median(P25- P75))

从表2的WSVM-Platt 和WSVM-Iso的评价指标可得,二者的AUC及SAR值的中位数均高于0.83和0.90,且WSVM-Platt的AUC值和SAR值的中位数、P25和P75均高于WSVM-Iso;WSVM-Platt和WSVM-Iso的RMSE中位数均低于0.07,且WSVM-Platt的RMSE值的中位数、P25和P75均低于WSVM-Iso,故Platt校准效果略优于Iso校准。

WRF-Platt、WRF-Iso和WRF的AUC和SAR中位数值均分别高于0.81和0.85。WRF-Platt和WRF-Iso与WRF相比,在AUC指标上,中位数、P25和P75取值接近;对比RMSE值可知,WRF-Platt和WRF-Iso的RMSE值的中位数、P25和P75均低于WRF对应的RMSE值,且WRF-Platt的上述三种取值均略低于WRF-Iso;WRF-Platt和WRF-Iso的SAR值的中位数、P25和P75均高于WRF,且WRF-Platt的上述三种取值均略高于WRF-Iso。由上可知,校准提高了WRF概率预测效果,且Platt校准效果略优于Iso校准。

讨 论

现阶段关于先心病及其他出生缺陷的研究多数集中在发生率的预测、影响因素的探索及分类预测等方面。杨峰利用决策树进行出生缺陷分类预测[2]。方俊群等利用判别分析和C5.0决策树对2007-2008年湖南省45家医院的出生缺陷患儿进行分类预测[3]。刘长云采用logitboost和分类树算法进行唇腭裂概率预测[4]。赵佳璐利用关联规则对出生缺陷进行概率预测[5]。Wang JF等采用SVM对和顺县1998-2005年出生的7880名婴儿进行出生缺陷分类预测[25]。Sainz JA等进行了先心病分类研究[26],Wieczorek A等利用心血管风险得分预测先心病。在出生缺陷的预测中,关于分类预测较多,基于全人群调查资料进行先心病概率预测的研究甚少[27]。

本研究基于代价敏感性和概率校准构建了先心病概率预测模型,预测结果符合预期。国内有关概率校准的研究相对较少。吕奕等对SVM和AdaBoost的概率预测结果进行Platt校准,然后将二者的校准概率和logistic回归的预测概率进行集成,结果显示,经过校准模型的预测效果提高[28]。沈翠华对SVM进行保序回归校准用于个人信用评估,预测效果优良[29]。从表2模型的对比可知,WSVM校准模型和logistic模型的预测结果都优于WRF及其校准模型,WRF虽然是性能优良的学习器,但不适合处理不平衡数据。WRF-Platt和WRF-Iso预测效果优于WRF,说明校准提高了模型概率预测性能。准确的预测概率对于预防先心病很关键,可为筛选先心病高危人群提供初步参考。

有关概率预测效果评价指标的选取,本文不仅选择了概率评价指标RMSE和AUC,同时采用了SAR评价指标。由于SAR包含了阈值评价指标ACC、等级评价指标AUC和概率评价指标RMSE,故而非常稳健。该指标提示校准提高了模型的概率预测性能[23]。

本文存在不足之处。第一,本研究仅选用了三种模型,在今后的研究中,将考虑建立其他模型如神经网络和深度学习等进行比较;第二,由于本文建立了综合变量,故而没有考虑交互作用。