地铁减振垫轨道结构对车致环境振动的影响分析

臧景超 杨新文 祁正海 马晓云

(1. 同济大学道路与交通工程教育部重点实验室，201804，上海；2. 兰州市轨道交通有限公司，730015，兰州//第一作者,硕士研究生)

环境振动问题目前已经成为影响城市地铁新线建设的瓶颈因素。地铁工程沿线环境敏感区段采取的减振类型主要包括特殊减振、高等减振和中等减振等3类。特殊减振一般采用钢弹簧浮置板轨道，高等减振一般采用梯形轨枕轨道或减振垫轨道，中等减振一般采用弹性扣件与压缩型扣件。本文主要对减振垫轨道的减振性能进行研究。国内外关于减振垫轨道的研究方法主要有理论分析、数值模拟和实验测试。文献[1]建立了地铁列车-板式减振垫轨道-下部基础有限元模型，对不同减振垫刚度下板式轨道的振动模态和动力响应进行了分析，并研究了隔振效果。文献[2]对隔离式橡胶浮置板轨道在不同工况下的固有频率、动力响应以及减振性能进行了分析。文献[3]对设置减振垫层的双块式无砟轨道分块长度进行了静力学分析。文献[4]建立了轨道-桥梁二维平面模型，并对桥梁上部减振垫轨道的减振性能进行了分析。文献[5]采用模态分析、谐响应分析法就不同道床板长度橡胶减振垫整体道床结构的固有频率、振型及传递函数等特性进行了研究。文献[6]采用数值计算方法对不同铺设方式的减振垫对橡胶浮置板轨道减振性能的影响进行了研究。

以上对减振垫轨道的研究大多集中于减振垫的刚度和减振垫的铺设方式等方面，而针对减振垫轨道结构对车致环境振动影响方面的研究还不够深入。因此，本文首先对减振垫轨道进行了模态分析，其次建立了地铁列车-减振垫轨道-隧道-土体-建筑物耦合系统有限元模型，计算分析了列车运行时道床板、隧道壁、地面和楼层的加速度水平和振级特性。研究结论可为地铁减振降噪设计提供一定的理论参考。

1 数值分析模型

1.1 模型建立

建立了地铁列车-减振垫轨道-隧道-土层-建筑物耦合系统数值模型，该模型的简化程度与计算结果的精确度和计算效率是矛盾的。为解决这些矛盾，将数值分析模型分为2个子模型。

(1) 子模型1为地铁列车-减振垫轨道模型，利用该模型计算得到列车在减振垫轨道上运行时的竖向轮轨力，并将该力作为子模型二的外界激励。

(2) 子模型2为减振垫轨道-隧道-土层-建筑物模型，通过该模型计算得到轨道板、隧道壁、地面和楼层的振动响应。

1.1.1 地铁列车-减振垫轨道模型

文献[7]基于车辆-轨道耦合动力学理论，建立了地铁列车-减振垫轨道耦合动力学数值模型，如图1所示。根据弹性力学势能原理，可求出系统的质量矩阵、阻尼矩阵、刚度矩阵和荷载向量。当地铁列车以速度v运行时,地铁车辆的动态平衡方程为：

KVzV(t)=QV(t)

(1)

式中：

MV,CV，KV——分别表示车辆系统的质量矩阵、阻尼矩阵和刚度矩阵；

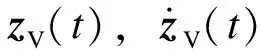
QV(t)——由轨道不平顺产生的动态荷载向量。

减振垫轨道的动态平衡方程在此不再赘述。在计算轮轨力时，该模型采用8节编组车辆。图2所示为竖向轮轨力计算结果。

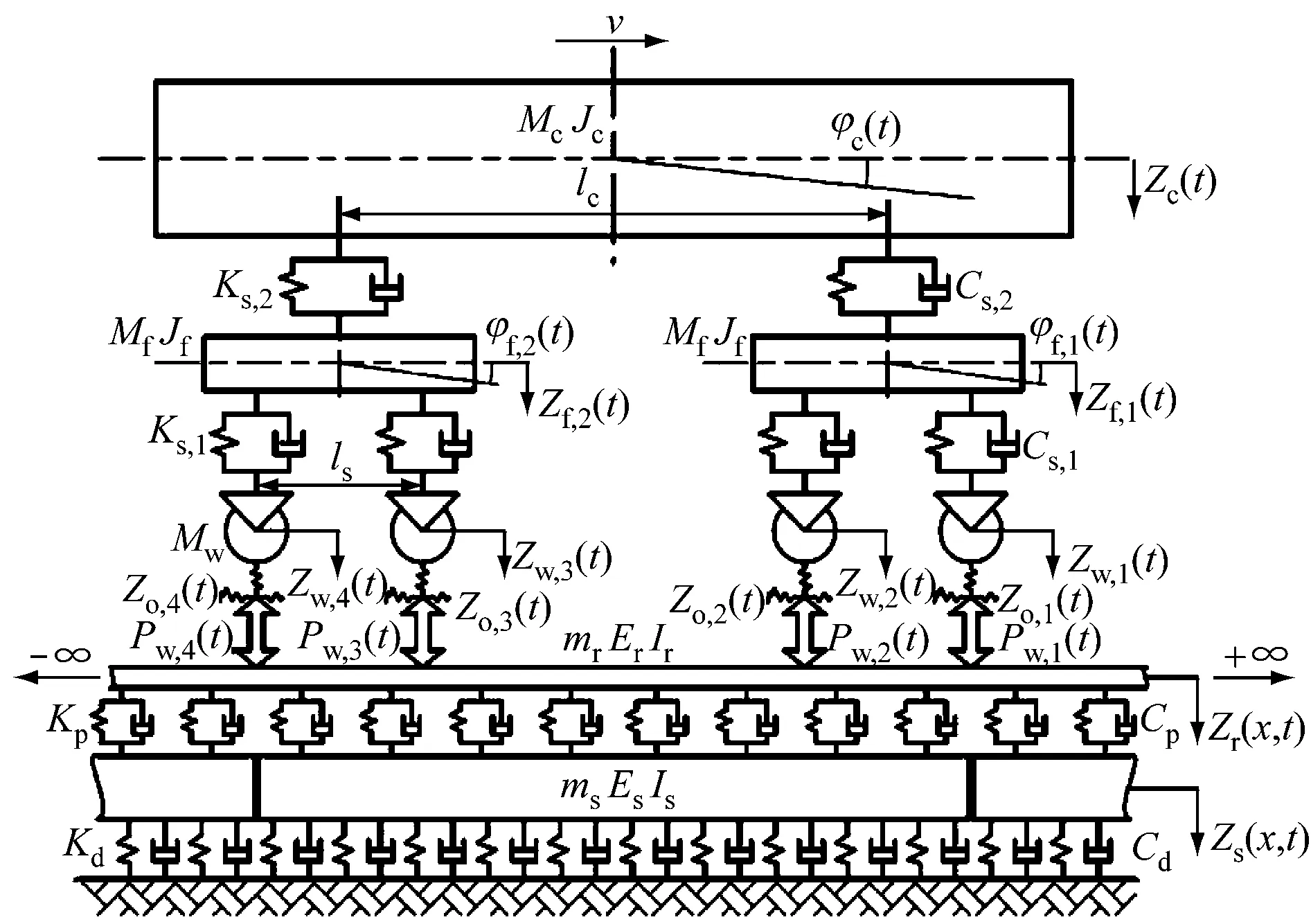
注:Mc、Mf、Mw分别代表车体、构架和轮对质量；Jc和Jf分别代表车体和构架的转动惯量.Ks,1和Ks,2分别代表一系悬挂和二系悬挂竖向刚度；Cs,1和Cs,2分别代表一系悬挂和二系悬挂阻尼系数；Zc(t)、Zf(t)、Zw(t)分别代表车体、构架和轮对的竖向位移；φc(t)和φf(t)分别代表车体和构架的摇头角;Pw,1(t),Pw,2(t),Pw,3(t)和Pw,4(t)均代表竖向轮轨力;Zo,1(t),Zo,2(t),Zo,3(t)和Zo,4(t)均代表轨道竖向不平顺;lc和ls分别代表车辆定距和轴距;Er和Es分别代表钢轨和轨道板的弹性模量；Ir和Is分别代表钢轨和轨道板的惯性矩;mr和ms分别代表钢轨和轨道板的单位质量;Kp和Kd分别代表扣件和CA砂浆的刚度;Cp和Cd分别代表扣件和CA砂浆的阻尼；Zr(x,t)和Zs(x,t)分别代表钢轨和轨道板的竖向位移

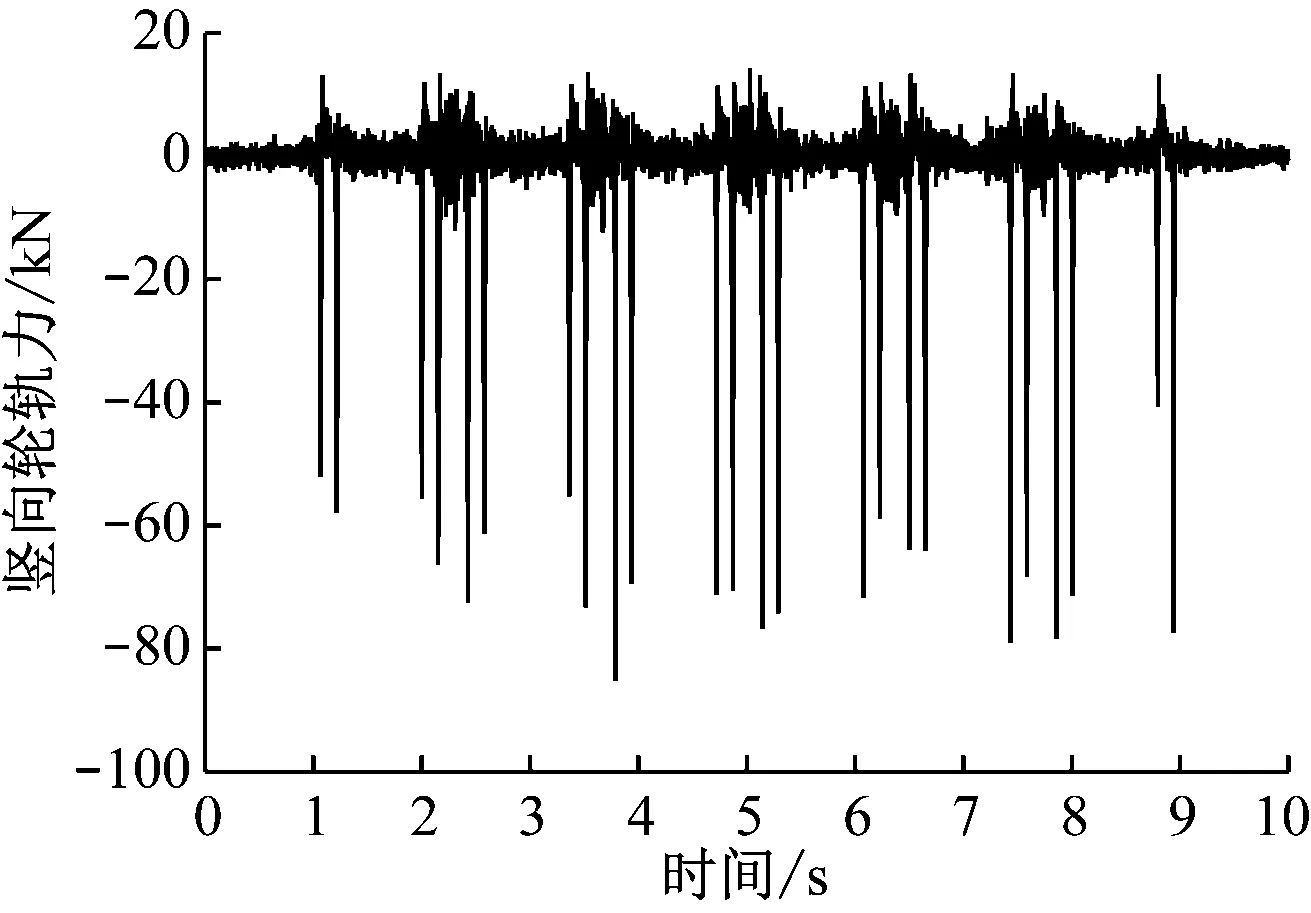
图2 竖向轮轨力时程曲线

1.1.2 减振垫轨道-隧道-土层-建筑物模型

采用ANSYS有限元软件建立减振垫轨道-隧道-土体-建筑物耦合系统有限元模型，如图3所示。

该隧道周围的地质情况参考了兰州市轨道交通1号线地勘资料，隧道周围土层模型有4层，从上到下依次为素填土、黄土状土、卵石土以及砂岩。该模型土层总厚度为40 m，宽度为40 m，纵向长度为25 m。模型中，楼房建筑结构为 6 层，每层高度为3 m，下部桩基础中桩的长度为10 m，桩底与持力较好的卵石层接触。模型中，轨道板、隧道仰拱、衬砌以及周围土体均采用8节点实体单元solid 45模拟，减振垫采用弹簧阻尼单元combin 14模拟，钢轨以及楼房的桩、梁、柱结构均采用梁单元beam 4模拟。

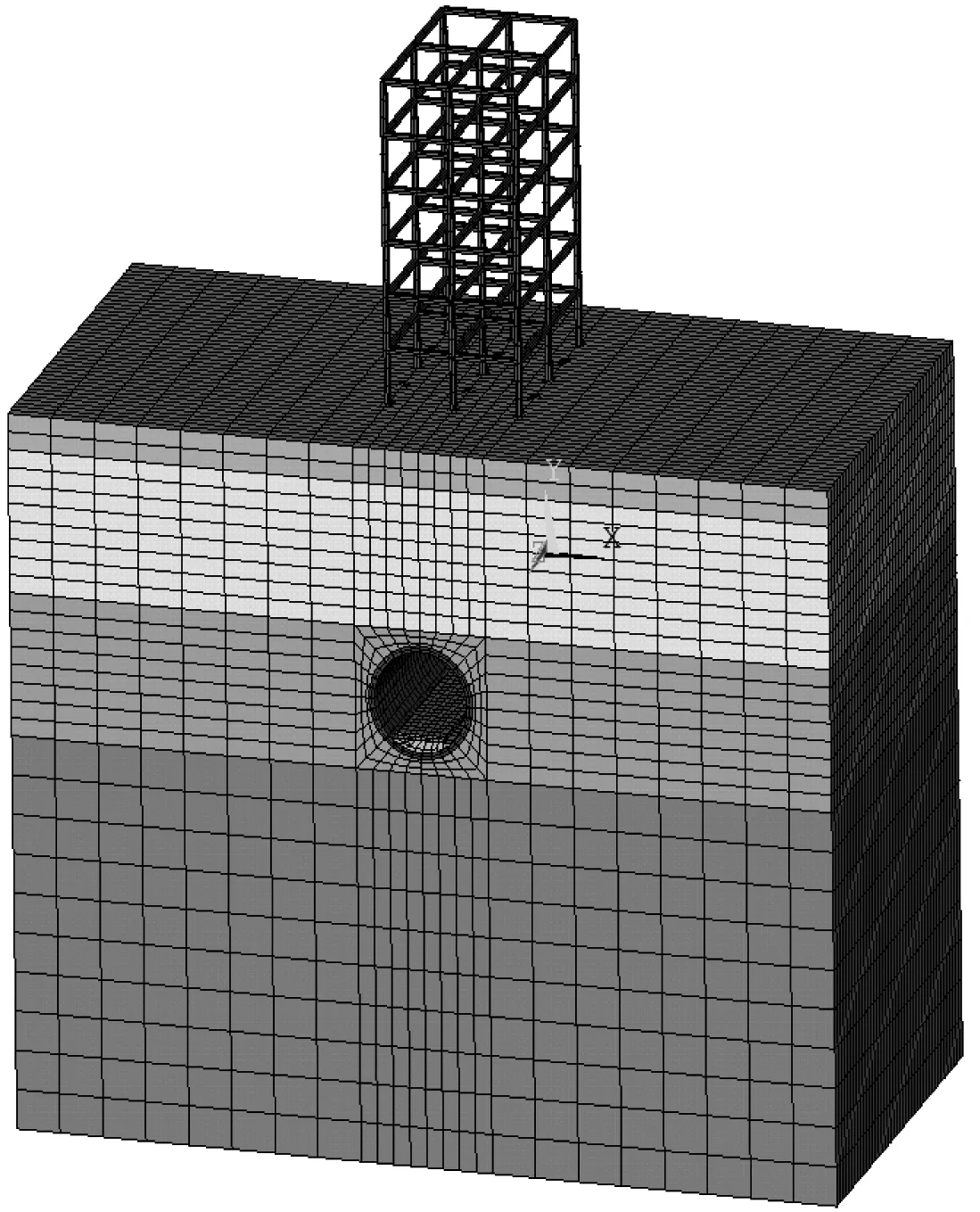
图3 减振垫轨道-隧道-土体-建筑物耦合模型

1.2 模型参数

子模型1中地铁车辆各部件计算参数均根据A型车进行选取，车辆轴重为160 kN，车辆定距为15.7 m，固定轴距为2.5 m。减振垫轨道结构中扣件刚度为4.0×107N/m，阻尼为7.5×104N·s/m；减振垫刚度为6.6×107N/m,阻尼为10×104N·s/m；轨道板的长度、宽度和厚度分别为25 m、3.25 m和0.35 m。子模型2中隧道衬砌厚度为0.5 m。土层的物理力学参数如表1所示。

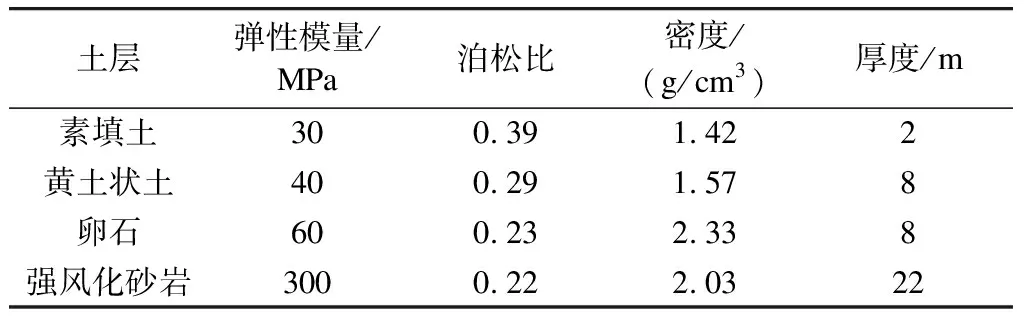
表1 土层的物理力学参数表

2 减振垫轨道板模态分析

轨道板模态分析是识别轨道板振动特性参数的重要方法。该方法被广泛应用于城市轨道交通领域。对兰州市轨道交通1号线使用的25 m长的减振垫轨道板进行模态分析。模型中，钢轨采用梁单元beam 4模拟，轨道板采用实体单元solid 45模拟，扣件和减振垫采用弹簧阻尼单元combin 14模拟，弹簧阻尼单元下部采用全约束边界条件。

提取减振垫轨道板的前10阶振型，如图4所示。由图4可知，减振垫轨道板第1阶和第2阶振型分别为轨道板的1阶弯曲和1阶扭转，第3阶和第4阶振型分别为轨道板的2阶弯曲和2阶扭转，第5～10阶如上所述，具有同样的规律。

a) 第1阶b) 第2阶c) 第3阶d) 第4阶e) 第5阶f) 第6阶g) 第7阶h) 第8阶i) 第9阶

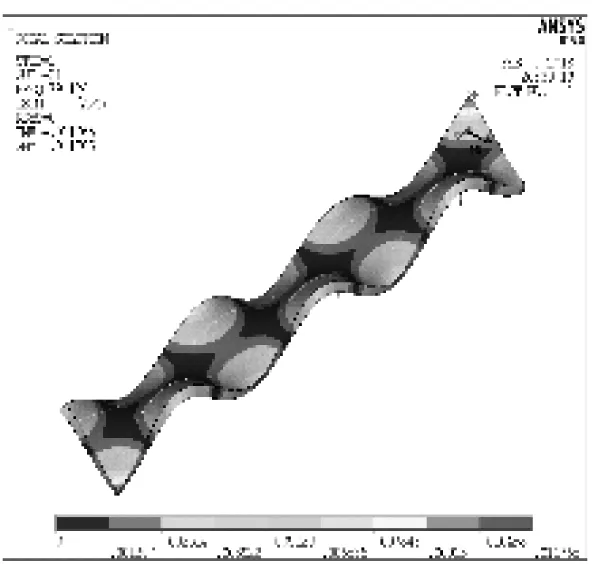
j) 第10阶

表2为减振垫轨道板前10阶振型的固有频率。由表2可知，25 m长的减振垫轨道板的前10阶振型的固有频率均小于80 Hz。

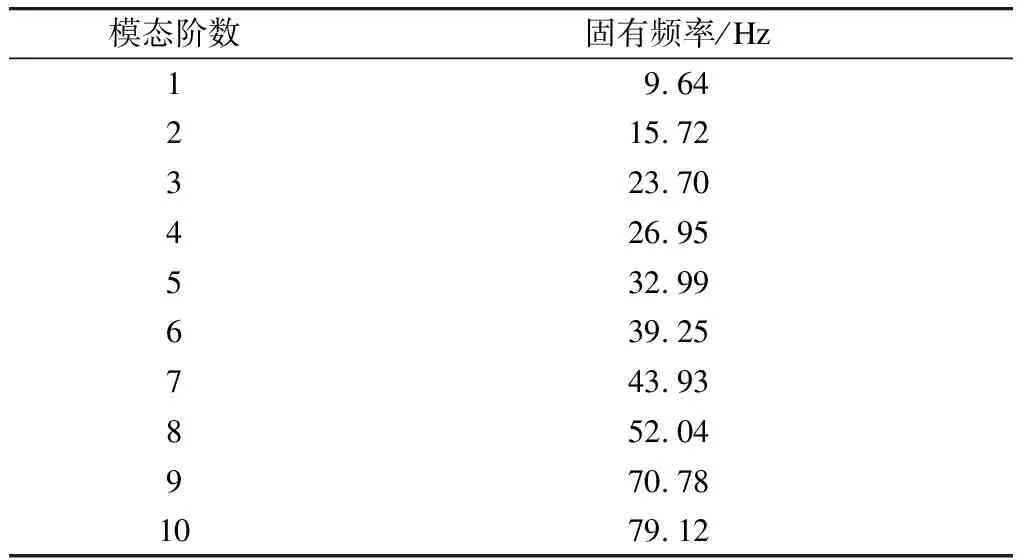
表2 减振垫轨道板前10阶固有频率表

3 车致环境振动分析

根据本文建立的数值分析模型，提取轨道板板顶、隧道壁、地面和楼层等结构计算点的竖向加速度(见图5)，并通过Matlab软件编制程序求出各计算点的1/3倍频程加速度级(见图6)，以及加速度Z振级最大值(见图7)。

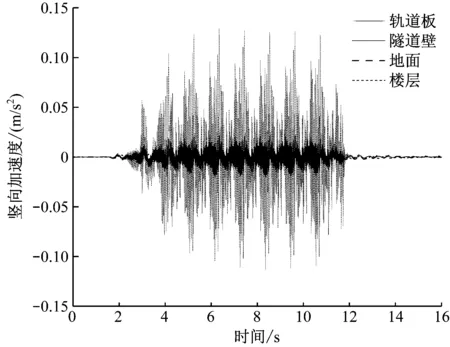
图5 不同计算点的竖向加速度时程曲线

由图5中轨道板加速度时域波形图波峰数目可明显看出，8节编组列车通过的振动变化规律，即列车通过计算点断面时轨道板、隧道壁、地面和楼层均从振动微弱开始，到出现32个振动峰值，最终振动减弱为0。而在同一断面处竖向加速度的大小由轨道板到隧道壁的衰减量远大于由隧道壁到地面的衰减量，这说明了减振垫轨道的减振作用主要体现在轨道结构上；隧道正上方地面和楼层的竖向加速度大小基本相等，这与文献[8]中得出的结论是一致的。

由图6可知，轨道板、隧道壁、地面和楼层的1/3倍频程加速度级整体变化趋势基本一致，均随中心频率呈先增大后减小、再增大再减小的特点；隧道内轨道板1/3倍频程加速度级比隧道壁大8～25 dB，隧道外中心频率小于50 Hz时地面和楼层的1/3倍频程加速度级相差基本处于10 dB以内。当中心频率为4 Hz、31.5 Hz和80 Hz时，各计算点的1/3倍频程加速度级变化曲线中出现3个明显的峰值。中心频率为31.5 Hz和80 Hz时出现的这两个峰值分别和减振垫轨道板的第5阶和第10阶振型的固有频率有关；中心频率为4 Hz时出现的这个峰值和整个系统模型的振型主频有关；中心频率超过31.5 Hz时，楼层和地面的1/3倍频程加速度级基本都小于40 dB。

由图7可知，轨道板、隧道壁、地面和楼层的加速度Z振级呈依次减小的趋势，且轨道板与隧道壁加速度Z振级的差值大于隧道壁与地面的差值。地面的Z振级最大值为69.51 dB，楼层的Z振级最大值为69.36 dB，均小于70 dB，符合文献[9]的要求。

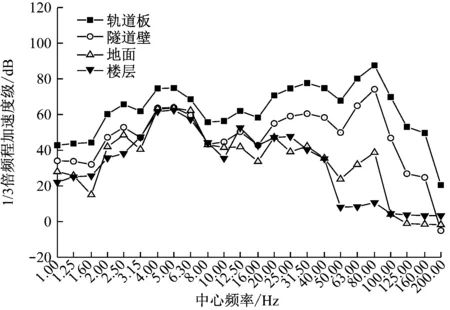
图6 不同计算点的1/3倍频程加速度级曲线

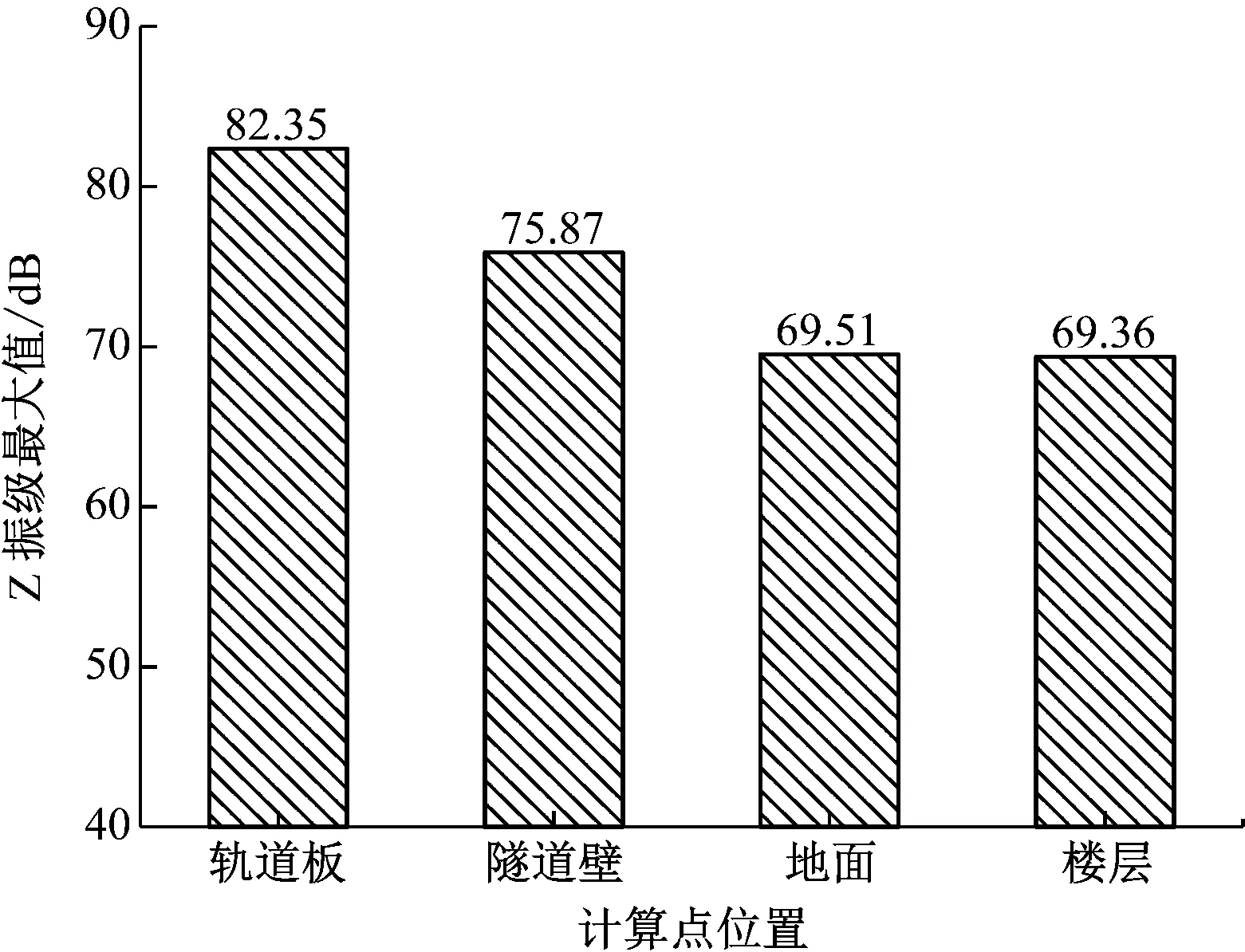
图7 模型结构中不同计算点的Z振级最大值

由于兰州市轨道交通1号线尚未开通，暂时无法通过现场试验来验证本文所建立的数值模型计算结果的精确度，现将本文的计算结果同已有文献中所选取的隧道埋深、建筑物避让距离及楼层数等现场条件与本文较类似的北京地铁15号线某建筑物内Z振级最大值的测试结果[10]进行对比，结果表明，文献[10]中测试的楼层Z振级最大值约为65 dB，这与本文计算结果(69.36 dB)的差值小于5 dB，由此可知，模型中计算结果的精确度是可以接受的。

4 结论

通过上述振动分析，得出以下结论：

(1)25 m长的减振垫轨道板的振型主要包括1阶弯曲、1阶扭转，2阶弯曲、2阶扭转以及多阶弯曲、多阶扭转，且前10阶固有频率均小于80 Hz。

(2)轨道板、隧道壁、地面和楼层的1/3倍频程加速度级曲线中出现的两个峰值对应的中心频率31.5 Hz和80 Hz与轨道板第5阶、第10阶主振型的固有频率有关，减振垫轨道的中心频率介于3.15 Hz和8 Hz之间时的减振效果较好。

(3)隧道埋深大于11 m，以及采用减振垫轨道结构的情况下，隧道正上方地面和楼层的Z振级最大值均小于70 dB，能够满足环评标准的要求。

(4)对比类似现场试验结果可知，本文所建立的数值模型可以较好地预测列车运营所致环境振动，在土层厚度和土质参数改变的情况下亦可作进一步推广应用。