基于多元线性回归的房价预测模型改进

张若天

（济宁孔子国际学校，山东济宁，272000）

0 引言

过去的十年里，我国经济蓬勃发展，房价也随之飞速提高，让大量的投资者从中攫取利益，也让无数人成为“房奴”，几乎人人都开始关注房价的波动走势，力图对房价做出科学有效的预测。因为房价的变动原因在经济学上仍有很大的争议，所以，预测也成为领域炙手可热的问题。

纵观全局，从2007年至2017年，各地房价都有了长足的提高，尤其是上海、浙江、江苏为首的东南沿海地区和以北京、天津为首的华北地区。

由于房价与国计民生休戚相关，房价预测无论是在经济学、数学还是计算机科学都成为了热门也同样十分困难的问题，因为其中涉及了许多随机影响因素，而且影响因素多元，无法通过简单的统计学模型进行预测。目前，学界对房价预测有了多种方法，如多元回归线性模型、灰色理论预测模型、马尔科夫预测模型、遗传算法和神经网络等等模型。

多元线性回归模型是一种常用的多元统计方法，原理明确，结构简单，在房价预测方面被十分广泛地运用，可是效果却不尽人意，常常在使用的过程当中出现各种各样的问题，而且近期一些“先进”的方法并不能从根本上解决这个问题，反而引入了额外的解释复杂性，多元线性回归模型的改进亟待解决。

本文瞄准中国楼市，基于多元线性回归模型，提出了自己的改进办法，本方法并未抛弃多元线性回归模型，而是从模型结果和因变量处理上提出了自己的看法，通过与其他的一些方法相结合，使组合模型的结果与实际情况更加吻合，更能使人信服，为人们提供更加优质的预测方法，必免一些不必要的麻烦。经过检验，本文提供的方法，可以在一定程度上提高房价预测的稳定性和准确性，使其更加实用。

1 模型介绍

1.1 多元线性回归模型

1.1.1 术语介绍

回归分析：一种统计学上分析数据的方法，目的在于了解两个或者多个变量之间是否相关、相关方向与强度，并建立数学模型以便于观察特定变量预测研究者感兴趣的变量。

1.1.2 模型引入

多元线性回归模型形式如下：

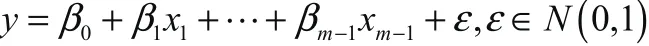
其中 β0,, β1…βm-1为待估参数，ε为误差，服从标准正态分布，对于待估参数的确定，有以下求解方法：

1.1.3 缺点论述

显然，多元线性回归模型有着难以避免的缺点。

第一，运用多元线性回归模型时，需要涉及大量的矩阵公式计算，因此，多元线性回归模型本身就具有计算量大和不易编程的特点，对人们的研究造成了极大的困扰，常常在一些不必要的地方进行不必要的计算，大大降低了模型的预测效率。

第二，多元线性回归模型极易受个别异常数据的影响，常常会在存在异常数据的情况中出现模型不符合其实际意义的问题，造成其自变量与因变量之间出现不合理的关系系数。如，符号相反，数值过大或过小，这时就需要更加稳健的回归方法对其进行优化和修改。

第三，多元线性回归模型计算过程中对最小二乘法有着极大的依赖性，但是，最小二乘估计中也有着一定的缺陷。其平方运算会使估计值与实际值之间产生一定的误差，若计算较为复杂的话，误差就会越积越大，严重脱离实际。

第四，多元回归线性模型不能实现跟踪响应变量变化，其估计值只能对一段时间内的结果产生较好的分析，如果是长期分析，就会显得有些捉襟见肘。

接下来，本文将提出一些改进这些问题的方法。

1.2 多元线性回归模型的改进

1.2.1 主流改进方法

为了改进朴素多元线性回归的若干缺点，目前有一些比较成熟的改进方法，如岭回归、稳健回归、主成分回归等，这些方法的复杂度都比较高，还可以使用偏最小二乘估计代替最小二乘估计进行待估参数的计算。要规避多元共线性，可以使用删减变量或者引入附加方程的房价进行处理。

1.2.2 基于灰色预测的多元线性回归模型

灰色预测是一种对含有不确定因素的系统进行预测的方法。灰色预测通过对各个变量进行关联分析，并对原始数据进行生成处理来寻找整个系统的变化规律，生成具有强烈规律性的数据数列，然后通过对预测的数据建立方程，从而得到其他关联数据的变化情况，来预测未来某一特定时间的某数据。灰色关联理论是邓教授创立的。其对少数据、贫信息不确定性问题的研究作出了重要的贡献。

（1）GM（1,1）模型

GM（1,1）模型有一个单变量的一阶微分方程构成。它主要用于复杂系统某一主导因素特征值拟合和预测，以揭示主导因素变化规律和未来发展变化趋势。

GM（1,1）模型不仅有连续的形式，还具有离散形式，而两者之间有着一定的联系。从其中的联系入手，便可得到离散GM（1,1）模型。

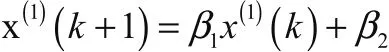
（2）灰色组合预测

与回归分析一样，灰色组合预测模型也是通过各个因素之间的关系而建立的预测模型，他将根据自变量与因变量所占的比重来建立模型。

其使用方法大致如下：得到各组序列后，通过灰色分析得出关联度系数序列，再得出自身的预测值。通过加权计算，得到一个最合理的权重，再对因变量序列中的预测值进行分析，基于灰色关联系数建立因变量预测值的回归模型，从而得到计算后位置元素的预测值。

运用灰色组合模型可以使预测值与自变量联系更加紧密，拟合度更高，从而参考价值更高，与其他更先进的回归模型得到的结果十分相近。

（3）灰色预测运用到多元线性回归

上文对灰色预测模型相关内容进行了介绍，易知，灰色预测模型具有能够跟踪响应变量动态变化、能够避免少量异常数据对预测值的影响，并且建模难度小的优点。因此，将其与多元线性回归模型相结合，可以对其缺点进行极大的弥补。

（4）应用方法

假设因变量y受到p个自变量的影响，现在有n组已知数据。首先，先计算灰色关联度，以确定影响因变量的主要因素，再将其按照灰色关联度排序，从而得到m个主要因素。然后在对数据进行分析，建立多元线性回归模型

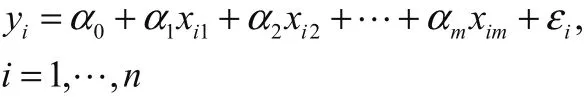
便得到了一个以（m个系数）为总体回归参数，且（m个误差）服从均值为0，方差为σ2的序列通过代入公式计算，得到各个回归参数的估计值。然后在用过灰色组合模型进行对自变量的预测，得到m个预测值，代入，便可得到灰色组合多元回归模型

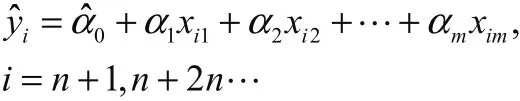
然后再对其进行拟合度计算，检验模型的准确度，做最后的调整，最终得出想要的预测值。

2 数据处理

2.1 介绍数据

数据是指对客观事件进行记录并可以鉴别的符号，是对客观事物的性质、状态以及相互关系等进行记载的物理符号或这些物理符号的组合。它是可识别的、抽象的符号。

数据虽然是抽象概念，但是，它也具有规模和属性。通俗来讲，数据规模就是数据的多少，数据越多，规模就越大，现在所说的大数据就是规模极大的数据；数据属性就是数据所具有的性质，数据具有的性质越多，我们称其属性越多，或维度越大，人们常说的数据降维处理就是尽可能地减少数据的无关属性，以达到筛选的目的。

同样，数据也有用来描述自己的单位，这个人们就接触的比较多。数据的单位常常被称作数据的宽度，日常生活中的网络速度、下载速度、存储空间等等都应用到了数据的单位方面的内容。

2.2 数据预处理的方法

数据预处理的主要方法就是数据清洗和数据归约。

数据清洗主要包括对数据集进行异常检测、识别并消除数据集中近似重复对象、对缺失数据进行清洗。数据集的异常检测主要就是消除少数异常数据对总体的影响，常常运用均值和标准差进行检测；重复记录的清洗主要就是筛掉重复的数据，使数据集更加精简，减少不必要的数据分析；对缺失数据的清洗与灰色预测模型有些相似，旨在对缺失数据进行预测，其中涉及了许多高级的理论方法，这里就不再一一描述。

数据归约主要包括高维数据的降维处理和离散化技术减少给定连续属性值的个数。高维数据降维处理其本质就是删除数据的冗余属性，避免其对预测过程造成影响，简化对数据分析的过程；而离散化技术减少给定连续属性值的个数这种方法大多数是递归进行的，看似花费了大量的时间，其实却节省了后面步骤的时间。

2.3 分析房价数据

对于房价数据而言，每一个数据维度都是具有现实意义的，因此如果想要降低数据维度，不能直接使用PCA、SVD等降维方法来降低数据复杂性，而是应该使用特征子集选择、特征创建方法。在处理某些特殊属性时，如“是否是学区房”、“是否有重大国家政策”等属性时，应该将原有数据处理成离散形式，如1代表“是”，0代表“否”等。在降低数据的复杂度之后，还应该使用简单的变量变换，对各个维度的数据进行规范化以消弭不同维度之间的数量级差别。在进行万以上处理之后，房价数据已经可以应用到我们的模型中。

3 结论

3.1 模型优势

本文的改进不仅保留了多元线性回归模型结构简单、原理明确的优点，而且避免了多元线性回归模型的各种缺点，使多元线性回归模型的应用更加广泛。同时，本文提出的模型还汲取了灰色预测模型的优势，使数据拟合度更高，更有价值去预测。

经过实例的验证，本文模型的构造是成功的，比传统多元线性回归模型要准确得多大大增强了本文提出模型的可行性，但还不能做到绝对的准确，还需进一步的研究。

3.2 改进方向

目前的数据量比较小，而且分布范围狭窄，基于统计学的模型无法发挥出最大的优势，因此之后的一个改进方向是寻找更多更可靠的数据来源，收集比较多的前期数据。除此之外，要想更加深刻地发现房价变动背后的规律，寻找更多的房价关联属性，即发掘更高的数据维度也是一个重要的改进方向，当数据维度足够高时，才能够还原出影响房价的更多细节。

目前本文在改进多元线性回归模型上做出的主要努力是结合了灰度预测模型，但是模型的整体复杂度尚有欠缺，无法拟合出数据更加复杂的变化，因此在现有的改进基础上，尝试将模型做得更加复杂也是使得模型具有更加良好表现的一种方法。除了以上的改进方向，对于迭代出的模型还应该有一个更加智能的函数来对当前模型进行打分以评判模型的好坏，有了这样的评价函数之后，模型的表现也会变得更好。