非自治具有食饵感染的捕食食饵竞争系统的持久性设计

李 超，郑 航，秦天红

（武夷学院 数学与计算机学院，福建 武夷山 354300）

1 研究的背景与意义

20世纪初，Lotka[1]、Voterra[2]最早提出著名Lotka-Voterra模型后，引发了对各类捕食者-被捕食者模型的研究热潮。传染病模型也是流行病学研究中重要的研究课题。Kermack等[3]在对流行病的独创性工作之后，流行病模型也一直有不少学者做了很多研究。这些年来，它们都得到了相当的发展。但将两个领域结合研究却在上世纪末才出现，此后越来越多研究者致力于将两者结合进行研究，于是出现了生态流行病学这种新的模型。

Anderson等[4]和Hadeler等[5]较早将种群生态学与流行病动力学相结合。随后，该领域的研究者们开始在不同的条件因素下，对有疾病传播的捕食模型进行了相应的研究。Venturino[6]，Chattopadhyay等[7]以及Xiao等[8]学者分别对疾病在食饵和捕食者之间传播的模型，并取得一些新的成果。张江山等[9]和杨亚莉等[10]通过对捕食系统中捕食者有疾病的生态流行病模型进行了研究，找到了平衡点并给出平衡点渐近稳定的条件。近几年，也不乏在对具有疾病感染的捕食系统的研究。王晓庆等[11]考虑疾病在食饵中传播的捕食食饵模型，证明了正平衡点的局部渐近稳定性，并讨论了引入时滞后正平衡点的稳定性。刘烁等[12]对具有垂直传播的SI捕食传染病模型进行研究，得到了关于平衡点全局渐近稳定的充要条件。章培军等[13]应用微分方程分支理论，讨论了食饵具有传染病和两时滞的捕食模型的稳定性和Hopf分支问题。王丽莎等[14]讨论了食饵感染疾病的Lotka-Voterra捕食-被捕食模型的平衡点及稳定、中心流形上的周期解，并给出了传染病流行的阈值。将捕食系统与流行病相结合起来研究，一直受到众多学者的关注和研究，中间也取得不少研究成果。但发现在结合二者的研究中大部分偏向于系统的有界性、平衡点、渐近稳定和Hopf分支等方面的研究，而对于系统持久性等方面的研究较少。受张艳[15]、胡新利[16]、钟小容[17]的启发，本文研究一类非自治具有食饵感染的捕食-食饵时间系统，假设系统中的食饵感染疾病，主要研究了该系统动力学行为，采用比较原理证明了该系统具有持久性并给出系统持久的条件。

2 非自治具有食饵感染的捕食食饵竞争系统模型

2.1 模型的建立

捕食食饵系统的模型是生态种群学的研究中比较常见的模型，而带有疾病的捕食食饵模型则是在将种群动力学与流行病动力学两者研究相结合后被建立的，因为在捕食系统中将流行病考虑到进去，符合实际同时也更加具有现实意义。二者的结合基本分为三种，分别是食饵具有流行病，只有捕食者有流行病以及捕食者和食饵均有流行病。

Kant等[18]曾对食饵感染疾病的捕食-被捕食者模型进行过讨论，具体模型如下：

式(1)考虑的模型是自治。但考虑到现实情况，模型中的参数可能会随着时间的变化而改变，所以考虑非自治的模型更能够体现实际情况。与此同时，除了物种之间有竞争之外，每一物种内部也存在竞争。因此本文将模型进行了改进，加入染病食饵内部竞争，捕食者内部竞争。改进后的非自治捕食食饵模型如下：

其中，S（t）是易感染食饵在时间t时的总数，I（t）是染病食饵在时间t时的总数，Y（t）是捕食者在时间t时的总数。其他参数的具体含义见表1。

表1 参数的具体含义Tab.1 The meaning of parameters

讨论主要围绕模型(2)展开，现假设r（t），K（t），p1（t），p2（t），β（t），c（t），d1（t），d2（t），k1（t），k2（t），e1（t），e2（t）是关于时间t的连续且严格大于零的函数，均有上界和下界。如果g（t）是定义在［0，+∞）上连续有界函数，引入记号：

2.2 持久性

引理1如果系统（S（0）＞0，I（0）＞0，Y（0）＞0），则（S（t）＞0，I（t）＞0，Y（t）＞0），即为(1)系统的正向不变集[19]。

证明：对于∀t∈［0，+∞）和（S（t），I（t），Y（t））T有

故系统(2)满足（S（0）＞0，I（0）＞0，Y（0）＞0）。解（S（t）＞0，I（t）＞0，Y（t）＞0），由此引理得证。

引理2如果a＞0，b＞0且，这里a是正常数[20]，有：

定理1为了方便讨论，引入下列记号：

若(2)系统满足下列（A1）～（A5）：

则称(2)系统具有持久性。

证明：假设X（t）＝｛S（t），I（t），Y（t）｝为满足初始条件的任意正解。 要证系统(2)是具有持久性，只需证明存在区域：

G＝｛（S（t），I（t），Y（t））T|m1≤S（t）≤M1，m2≤I（t）≤M2，m3≤Y（t）≤M3｝⊂int R3+，使得存在T＞0，当t＞T时，使得X（t）∈G其中mi，Mi分别满足：

其中ε为大于零又充分小的正数。

从(2)系统的第1个方程，可以作出如下推导：

由引理2和式(3)，可以得到：

由(2)系统的第2个方程及(5)式，当t≥T0时，可作如下推导：

根据引理2和(6)式，可以得到：

同理，由(2)的第3个方程及式(5)、(8)，当t≥T1时，可进行如下推导：

根据引理2和式(9)，可以得到：

由(10)式，对ε＞0且充分小，使得

由比较原理可知，存在T2＞T1，当t＞T2时，有

由(2)的第1个方程及(7)式和(10)式，当t≥T2时，有可作出如下推导：

根据引理2和式(12)，可以得到

由式(13)，对ε＞0且充分小，可使：

由比较原理可知，存在T3≥T2，当t≥T3时，有

由(2)的第2个方程，(11)和(14)式，当t≥T3时，可进行如下推导：

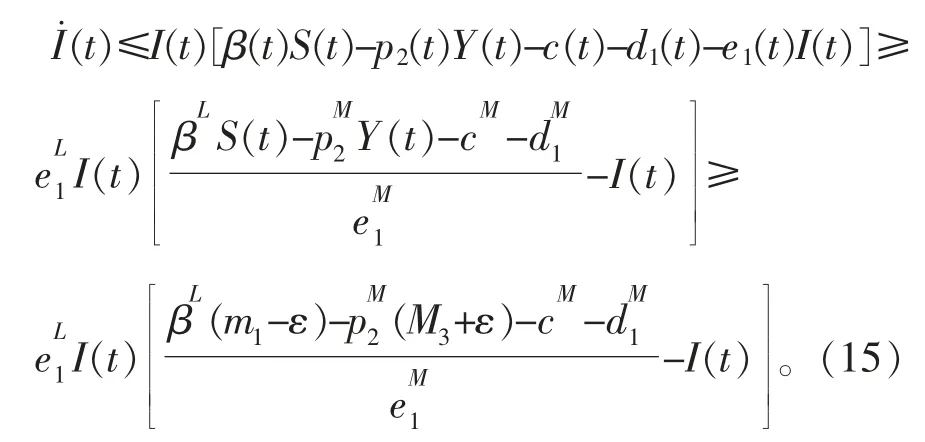
根据引理2和(15)，可以得到

由(2)的第三个方程及式(14)、(17)，当t≥T4时，可作如下推导：

由引理2以及(18)式，有

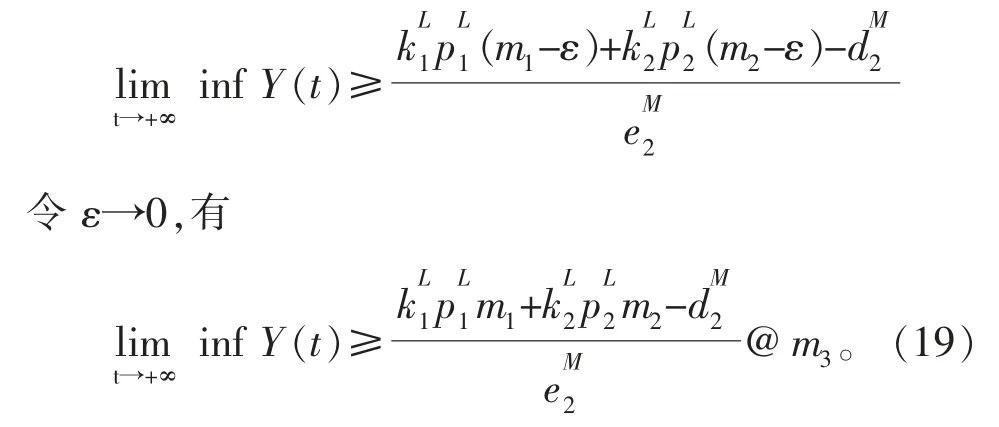
综上所述，令T≥T4，当t≥T，有m1≤S（t）≤M1，m2≤I（t）≤M2，m3≤Y（t）≤M3，即当t≥T时，X（t）=｛S（t）,I（t）,Y（t）｝∈G，同时系统满足定理1，故(2)系统具有持久性。