桉树人工林单木材种出材率表的研制

严 洪

（福建省林业调查规划院，福建 福州 350003）

蓄积量(记作M)是森林生产力的重要指标，而出材量是森林商业用材价值的衡量标准[1]，其中出材率是蓄积量转化为出材量计量单位，因此，在森林经营管理过程中，确定森林出材率显得十分重要[2]。实践表明，编制出材率表，确定森林收获量，可以很好地发挥森林资源资产调查成果的作用，在森林资源档案管理的科学性、时效性和连续性等方面都具有十分重要的意义。20世纪50至60年代间，采用手绘曲线技术编制材种出材率表，但存在数表内容过于繁琐的问题，同时常出现生产上造材需要的材种与规定材种不一致问题，造成这种方式编制的出材率未在林业生产实践上普遍应用。而通过利用材积比和削度方程[3]编制出材率表的技术在生产上得到认可，且随着现代计算能力的发展，利用树干削度方程编制出材率表的思路是目前及今后一段时间内研究发展的趋势。因此，本文拟以桉树为对象，采用削度方程编制桉树单木材种出材率表。

桉树（Eucalyptus robusta）是桃金娘科桉属树种的统称，被誉为世界四大速生树种之一。随着天然林、重点区位人工商品林限制采伐政策相继出台，作为速生纤维、实木加工短周期工业原料林，桉树人工林建设在水热条件较好的福建南部地区发展迅速。由于桉树种植历史不长，目前缺乏适用于南部地区的桉树出材率表，相关研究也较少[4-6]。本研究利用现有削度方程研究成果，对常见的削度方程进行拟合对比，寻求适合于福建省境内桉树人工林的最佳削度方程，以此为基础编制桉树单木材种出材率表，为林业生产应用提供便利。

1 基础数据

为保证数表编制成果的适用性，在样本组织方面尽可能扩大样本变量的覆盖范围，以科学反映各变量间相关规律的真实性、完整性和稳定性，提高预估精度，以扩大模型应用时的外推范围，减少外推偏差[5，7]。本研究样木数据覆盖福建省桉树主要种植区，涉及的行政区主要有漳州全市、泉州全市及永安、闽清、连江、罗源、闽侯等县（市），在桉树正常生长人工林中，区分不同立地条件、种植密度和年龄，按随机抽样方式采集553株样木，确保每个径阶和树高级均有相应的样木。

确定样木后，按材种划分标准和造材原则进行现场造材，并利用区分求积式计算各材种材积[6]。将所有样木按胸径和树高从小到大的顺序排序并按1、2、3编号分成3组，其中编号1、3组样木共计369株用于建模，编号2组样木计184株用于检验。样木的基本信息见表1。

表1 桉树人工林样木基本信息Tab.1 Basic information of eucalyptus robusta sample wood

2 研究方法

2.1 编表原理

由于削度方程是描述林木树干任意高度处直径的变化规律模型，即不仅能描述林木树干形状变化规律，而且能够估计任意段的材积(V)，因此本次通过建立削度方程来编制桉树单木材种出材率表，其通式为：

式中：H为林木树高；D为林木胸高去皮直径；h为林木任意离地高度；d为林木树干任意高度h处的去皮直径。

通过该方式编制桉树单木材种出材率表过程中，还需要建立桉树胸径预估模型、树高曲线模型、去皮材积比模型。

2.2 削度方程

为了提高桉树材种出材率预估精度，本次选择国内外常见、较有代表性的7个削度方程作为备选模型，见式(2)～式(8),并利用常见的模型拟合精度评价指标评估模型拟合效果，包括剩余标准差、相对误差平均值（系统误差）、相对误差绝对值的平均值（平均误差）、相关指数等4个指标，确定最佳的桉树人工林的削度方程：

式中：ai(i=0、1、2、3、4、5)为参数，Z=h/H。

2.3 参数求解

削度方程为非线性方程，难以用常规的回归分析法估计参数，本次研究采用免疫进化算法解决这一问题。该算法受生物免疫机制的启发而形成的一种智能算法，估算桉树削度方程的大致步骤为：①确定模型优化问题的表达模式；②生成初始群体，计算适应度，并确定最优个体；③根据免疫进化算法子代个体的生成式(9)、式(10)进行进化操作，并生成子代群体；④根据生成的子代群体，确定最优个体，若个体不佳，则重复操作③，直至生成最优个体，并作为寻优结果。

式中：Xt+1为生成的子代可行解；为最优父代；St为父代标准差；St+1为子代标准差；N（0,1）为随机数。

2.4 去皮胸径预估模型

在森林调查中，每木检尺为带皮直径，而材种材积为去皮材积。对于削度方程中的去皮胸径，由带皮胸径按下式估计：

式中：d为去皮胸径；D为带皮胸径；a、b为待定参数，根据样木资料，用最小二乘法估计。

缓解现阶段美术教学中出现问题的解决方法是采用“具象表现绘画”的教学方法，具象表现绘画的基本方法既可以避免传统具象写实的客观地死板呈现，又减弱了现代极端化的主观表现，同时还培养学生独特的的观察能力以及创造力。

2.5 去皮材积比模型

去皮材积比是树干去皮材积占带皮材积的比值，利用削度方程求各材种去皮材积占树干去皮总材积百分比后，乘以去皮材积比将其转换为占树干带皮材积百分比，即材种出材率。去皮材积比模型如下：

式中：Kν为去皮材积比；D为带皮胸径；H为树高；a、b为待定参数，采用最小二乘法估计。

2.6 树高级指数模型

根据林分胸径与树高的关系，把相同林分平均胸径对应的不同林分平均高分为若干等级称作树高级，基准胸径时对应的树高称作树高级指数。为便于生产应用，分别树高级指数编制材种出材率表。选择科夫方程建立树高曲线模型，方程式如下：

基准胸径为D0时，树高级指数模型为：

3 结果分析

3.1 削度方程

利用建模样木资料，采用免疫进化算法求解备选削度方程参数，并计算剩余标准差、系统误差、平均误差和相关指数，结果如下表所示。

相关指数是反映削度方程拟合效果的常用指标，要求越接近于1越理想。因此，在编制材种出材率表时，应尽量挑选出相关指数大的削度方程。上述削度方程的相关指数均在0.900以上，但各方程之间的差异还是比较明显的，以式(3)、式(6)、式(8)效果理想，相关指数明显大于其他方程，最大者为式(8)，相关指数达0.983。

表2 削度方程求解结果Tab.2 Solution results of taper equation

剩余标准差是反映削度方程拟合效果的另一个常用统计指标，要求剩余标准差越小越好。在建立削度方程时，应尽量挑选出剩余标准差小的模型。7个备选削度方程中，剩余标准差最小的是式(8)，其次是式(3)和式(6)，与其他削度方程相比，这3个方程从剩余标准差来看是比较理想的。

系统误差存在正负误差互相抵消的情况，反映了每个样本单元直径实测值与其相应削度方程理论值的相对误差的整体平均水平，是从整体上考察削度方程是否存在系统性偏大或偏小的问题，以越接近于0越好，一般要求在正负3%的范围内为宜。满足这一要求的削度方程有式(3)、式(6)、式(7)、式(8)，尤以式(8)最好，系统误差小于2%。

相关指数、剩余标准差、系统误差、平均误差分别从不同角度反映了在胸径、树高和离地面高度三个测树因子的控制下，备选削度方程的拟合效果和预估精度。综上分析，式(8)是最佳削度方程，将其应用于编制桉树材种出材率表，具体表达式如下：

式中：d为树干上h高度处的去皮直径,h为离地面高度,D为胸高去皮直径,H为树高，Z=h/H。

3.2 去皮胸径预估模型

利用建模样木资料，以带皮胸径为辅助变量，去皮胸径为预估变量，采用最小二乘法建立去皮胸径预估模型：

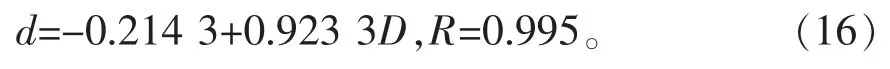
3.3 去皮材积比模型

利用建模样木资料，采用中央断面区分求积式计算每株样木的去皮材积和带皮材积，并计算去皮材积比，用免疫进化算法求解模型参数，结果如下：

3.4 树高级指数模型

利用建模样木资料，选择科夫方程作为树高曲线模型，采用免疫进化算法求解模型参数，取基准胸径为D0＝20 cm建立树高级指数模型：

也可简化成下式：

3.5 出材率表的编制

材种划分延续以往林业木材生产的材种规格并参考国家材种划分标准确定，即在福建省原有材种规格的基础上，对规格材区分为大原木、中原木、小原木三种，经济材具体标准见表3。

表3 经济材材种划分标准Tab.3 Division standard of economic timber species

以削度方程为基础，结合其他相关测树因子模型编制材种出材率表的步骤如下：给定树高级指数，将径阶中值（带皮胸径）代入式(16)计算去皮胸径，分别用式(17)、式(18)计算去皮材积比、径阶树高；用式(15)分别计算各材种小头去皮直径、材长、出材量和树干去皮总材积。将材种出材量占树干去皮总材积的百分比，乘以去皮材积比，得相应出材率。将出材率计算结果按表4（树高级指数为18 m）格式整理，即完成材种出材率表的编制。

3.6 出材率表的检验

用184株检验样木对出材率表进行适用性检验，计算系统误差和平均误差，结果见表5。

表4 桉树人工林单木材种出材率表Tab.4 Eucalyptus robusta single timber species outturn table

表5 出材率表适用性检验结果Tab.5 Applicability test results of outturn table

适用性检验结果表明：基于削度方程编制的桉树人工林材种出材率表精度满足要求，可为林业生产应用提供参考依据。

4 结论和讨论

多削度方程拟合对比表明：式(8)是最佳方程，能客观反映桉树人工林树干形状的变化规律，具有精度高、误差小等优点，可用于估测立木材积、出材量（或出材率）。基于此编制的桉树人工林单木材种出材率表适用，可为森林资源调查和经济评价等方面提供参考依据。

利用削度方程预估直径，理论上应满足以下2个基本条件：(1)当树干离地面高度h＝1.3 m时，由削度方程估算的直径与实际胸径相符；(2)当树干离地面高度等于树高即h=H时，上部直径d＝0。在备选的7个削度方程中，能同时满足这2个基本条件的只有式(5)和式(8)。但式(5)只有1个参数a0，是以树干各部位的形状相同为前提条件的，没有考虑到树干各部位的形状是随着相对高（h/H）的变化而变化的。仅有式(8)为相对高的函数。以上2方面都从理论上进一步证明了式(8)是最佳方程。

以削度方程为基础编制材种出材率表，可以适应材种规格变化的需要，比采用实际造材样木编制材种出材率表经济、高效。但运用削度方程编制出材率表，没有考虑树干病腐、弯曲、枝节等质量因素及造材损失对材种出材率的影响，估测结果是无材质缺陷的健康木出材率。因此，应用中须根据生产经验，明确修正参数，提高林分材种出材量的测算精度。

式(8)属于干形参数可变的削度方程，在估计任意部位直径时显示出明显的优越性。但该方程无法推导出编制出材率表时所必须的材长方程和材积比方程，实际应用时都要进行迭代计算和数值积分（区分求积）确定各种规格的材长、出材量和总材积，计算比较烦琐。希望在今后改进研究中能得以解决。