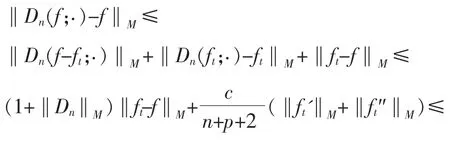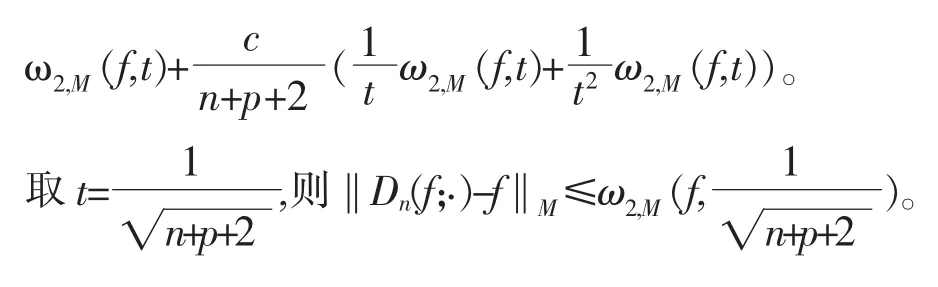Schurer型Durrmeyer算子在Orlicz空间内的逼近

任美英

（武夷学院 数学与计算机学院，福建 武夷山 354300）

近年来，很多学者专注Orlicz空间中算子逼近问题的研究，获得较多研究成果[1-7]。Cabulea等（2002）[8]引进如下Schurer型Durrmeyer算子：

Cǎbulea等[8]研究了算子Dn（f；.）在连续函数空间的逼近性质。本文的目的是研究该算子在Orlicz空间内的逼近性质。

首先，引入Orlicz空间的一些相关概念。

用M（u）和N（ν）表示互余的N函数,有关N函数的概念可见吴从炘[9]文献。由N函数M（u）在区间[0,1]上生成的Orlicz空间是指具有有限的Orlicz范数的可测函数的全体｛u（x）｝，其中是ν（x）关于N（ν）的膜。由吴从炘等[9]研究可知，Orlicz空间的Orlicz范数也可以表示为：

Orlicz空间中f（x）的一阶和二阶连续模分别定义为：

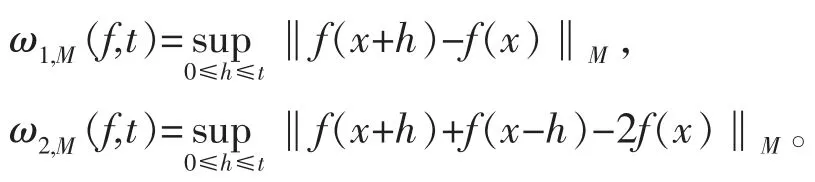
若存在u0＞0，k＞0，使得当u≥u0时，有M（2u）≤kM（u），则称N函数M（u）满足Δ2一条件[9]。

由Ramazanov（1984）[10]研究可知，ω1,M（f,t）→0（t→0）,ω2,M（f,t）→0（t→0）当且仅当N函数M（u）满足Δ2一条件。

c表示与f，n无关的正常数，在不同处可以表示不同的值。

定理1Dn（f；.）是从到的有界线性算子，且‖Dn‖M≤1。

定理2设M（·）满足Δ2一条件，则对于,当n+p≥3时，有

定理3设M（·）满足Δ2一条件，则对于,当n+p≥3时，有

2 几个引理

引理1[8]对于（1）式给出的算子Dn（f；.），有

1）Dn（1;x）＝1；

2）Dn（t;x）＝

3）Dn（t2;x）=

引理2对于（1）式给出的算子Dn（f；.），

2）当n+p≥3时，Dn（（t-x）2;x）

证明：

引理3[10]设M（·）满足Δ2一条件，则对于有,且‖θf（x）‖M≤c‖f‖M，其中是函数f（x）的Hardy极大函数。

引理4对于上述，当n+p≥3时，有

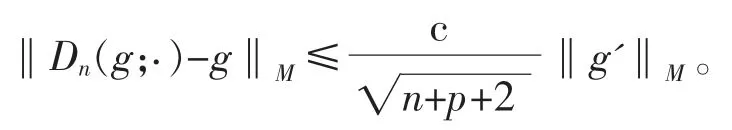
证明：对于x∈[0,1]，由引理1得

由正线性算子的Cauchy-Schwarz不等式及引理2得

再由引理3知，

引理5[11]对于，有

2 定理的证明

定理1由于故由N函数凸性、积分型Jensen不等式得

显然，算子Dn（f；.）是线性的，因此Dn（f；.）是从到的有界线算子，且‖Dn‖M≤1。

定理2对及引理4中的，当n+p≥3时，

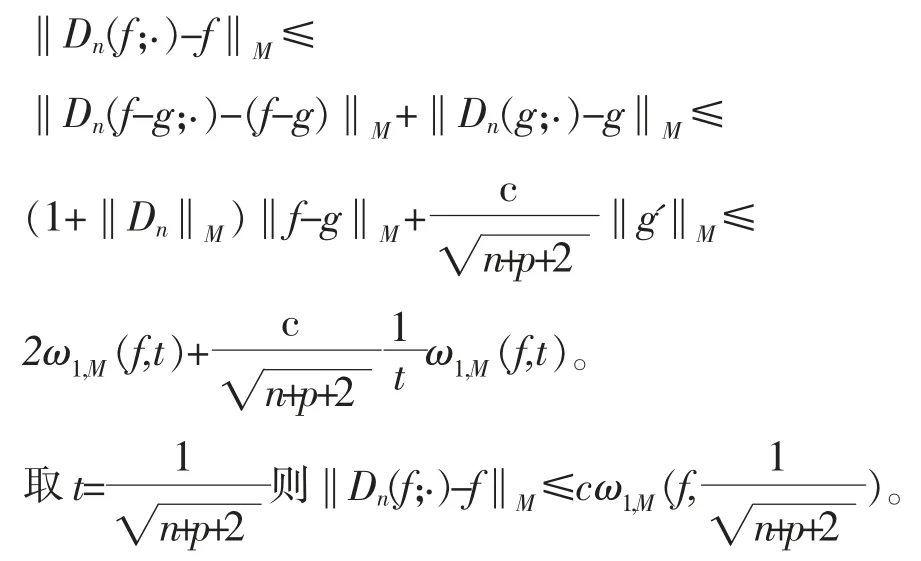
定理3（1）设，当n+p≥3时，由拉格朗日中值定理和引理2得

于是，由相关文献［9］和引理3知