基于改进Adam优化器的CNN电镜医学图像分类

汪友明, 徐攀峰

(西安邮电大学 自动化学院, 陕西 西安 710121)

电子显微镜(电镜)向固体样本发射具有一定能量的电子束，与样本原子的原子核和电子发生弹性和非弹性散射，激发样本产生多种物理信号，从而产生电镜图像。应用于医疗领域的电镜医学图像为疾病的诊断提供了科学的依据，在疾病的诊断中起着举足轻重的作用。

随着技术的发展、患病人数的增长以及疾病种类的增多，使得电镜医学图像数据呈爆炸式增长，大量的医学图像只有经过科学地分类才能利用计算机技术对医学图像进行分析、计算和处理，才能从医学图像中挖掘出蕴含在图像内丰富的特征信息和规则，辅助医生进行临床诊断。

近年来，随着深度学习的提出，神经网络方法成为最常用的图像分类方法之一[1]。针对人为设计模型的不完备性[2-4]，深度学习采用机器学习的方式对数据进行表征学习[5]，将对图像特征的学习融入到建立模型的过程中，通过构建具有多隐层的网络学习模型和训练大量数据样本，来获取有用的特征，从而提升图像分类的准确性。

卷积神经网络(convolutional neural networks, CNN)算法包含卷积计算且具有深度结构的神经网络(neural networks, NN)，是深度学习(deep learning)的代表算法之一，近些年来被应用于电镜医学图像的分类之中，如分类霍乱和流行疟疾的微观图像[6]、鼻腔细胞学制剂细胞图像[7]、细胞图像的分类与跟踪[8]等。或者利用将CNN算法与递归神经网络(recurrent neural network, RNN)算法相结合的CNN-RNN图像分类算法[9]，实现医学图像分类。

CNN方法使用优化器来计算和更新影响模型训练和输出的各项网络参数，使其逐步逼近并达到最优值，从而最小化或最大化损失函数，以优化网络的更新迭代方式，提高迭代效率[10]。

常见的优化器包括梯度下降算法优化器、自适应梯度算法优化器、Adagrad、RMSProp和自适应矩估计(adaptive moment estimation, Adam)算法优化器等。Adam优化器结合了AdaGrad和RMSProp两种优化算法的优点，能够综合考虑对梯度的一阶矩估计(first moment estimation)和二阶矩估计(second moment estimation)计算出更新步长。另外，Adam优化器中的超参数具有很好的解释性，通常无需调整或仅需很少的微调，就能将更新的步长限制在一定的范围内，十分适合应用于大规模数据及参数的场景，是一种比较理想的大数据处理工具[11]。不过，当待处理的图像较多、较复杂时，Adam优化器存在着迭代曲线振荡变化，收敛性能较差等问题[12]。

为了提高CNN方法处理电镜医学图像的分类精度和算法的稳定性，本文拟提出一种改进的自适应Adam优化器方法。通过添加修正因子，以下降趋势的幂指数学习率为基础，利用前一阶段的梯度值与当前阶段梯度值进行对比、调节，更新和计算影响模型训练和模型输出的网络参数，逼近网络的最优值。

1 CNN与Adam优化器

1.1 CNN

CNN本质上是一种输入到输出的映射。通过训练，CNN就会自动获得这种映射能力，而不需要推导精确的代数表达式。由于相同特征映射面上的神经模块间权值相同，所以网络可以在并行模式下进行学习，这也是卷积神经网络相对其他网络模型的一大优势[13]。

利用反向传播算法以及有监督的训练方式[14]训练卷积神经网络，将网络输出结果与预先设定的标签进行比较，计算并输出误差项。根据反向传播的思想，将误差逐层传递到每个结点，并对权值进行更新。通过不断迭代训练，网络的误差项会越来越小，权值更新幅度也越来越小。当权值逐渐趋于稳定时，就完成了网络的训练任务[15]。

图像都有其代表性的特征。从图像某一区域学习到一些特征后，就可以将这些特征用作探测器，扩展到所有区域中去，获得不同区域的激活值。卷积操作的目的是提取样本数据的输入特征，第一卷积层通常只会提取一些初级的特征，如边、线、角等基本层级，多层卷积神经网络则会提取更复杂、更关键的特征。

卷积神经网络模型结构如图1所示。

图1 卷积神经网络模型结构

在卷积神经网络中，图像数据经过卷积处理，能够增加训练集的数量，提高数据的特征维数，但是有可能导致维数灾难的发生[16]。为了改善这一问题，首先需要对卷积得到的特征图进行聚合池化处理。池化处理能够在有效地降低输出特征图分辨率的同时，仍然可以稳定地保持着高分辨率时的特征。将经过池化处理后图像数据经过全连接网络[16]处理，就能够利用权值矩阵将前面提取的局部特征重新组合成完整的图像。全连接层的各个神经模块结点都与上一层输出的特征图中的神经模块结点相连接。其次，利用优化器对全连接网络处理后的图像进行处理，用以更新和计算影响模型训练和模型输出的网络参数，使其逼近或达到最优值。最后，将数据通过softmax分类器，并输出相应的分类结果。

1.2 Adam优化器

Adam优化器算法[17-19]基于训练数据迭代地更新神经网络权重，对随机目标函数执行一阶梯度优化。Adam算法梯度的对角缩放具有不变性，适合求解带有大规模数据或参数，解决大噪声和稀疏梯度的非稳态问题。Adam优化器的基本算法可以描述如下。

设定噪声目标函数ft(θ)，它是参数θ在t期(第t次迭代)的随机函数。为了减小该函数的期望大小，需要使用随机性描述小批量样本函数噪声，计算目标函数关于参数θ的梯度

gt=θft(θ)。

(1)

第t期梯度的指数移动均值mt和平方梯度vt的表达式分别为

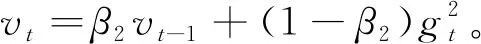
(2)

其中参数β1、β2∈[0, 1)代表制移动均值指数的衰减率。在初始时间和衰减率很小的情况下，矩估计值会偏向0。

(3)

令初始化平方梯度均值为0，则平方梯度均值在第t期的更新表达式为

(4)

每迭代一步，都要更新参数θ的取值，θ的更新表达式为

(5)

其中：η为学习率，表示参数空间有效步长的量级；ε=10-8表示一个常数参量。通过参数更新，实现算法迭代，使得目标函数逐步向最优取值收敛。

Adam优化器算法中，修正了一阶矩到非中心的二阶矩估计，减小了偏置量，但在对复杂、大规模的电镜图像分类处理中，该算法迭代曲线振荡变化较剧烈，收敛性能较差。

2 基于改进Adam优化器的图像分类

2.1 图像预处理

图像预处理是将图像数据经过一些简单的处理后再交给识别模块识别。图像预处理的主要目的是减少或消除图像中无关的信息，恢复有用的真实信息，增强有效信息的可检测性，最大限度地简化数据特征，从而改进后续处理中数据特征提取、图像识别、图像分割的可靠性。本文采用高斯滤波方法去除图像噪声。

2.2 模型训练

模型训练是指获得实验数据后，通过对有标签数据进行训练，获得一个模型，然后通过构建的模型，给新数据添加上特定标签的过程。在分类实验中，给新数据加上了特定的标签，就得到了它的类别属性。

CNN图像分类是在对原始图像信息进行计算的基础上完成的。原始图像通过卷积、池化层的特征提取，通过训练得到输入输出间的映射关系，它是原始图像到类别分值的一种映射。

采用损失函数来衡量训练效果的指标。通过计算损失函数[20]，可以得到计算结果与设定标签之间的误差，用来量化预测分类标签与设定标签之间的一致性。

应用交叉熵损失函数判断预测取值与目标取值之间的距离。交叉熵损失函数[20]的表达式为

Loss=-[ylogy+(1-y) log (1-y)]。

(6)

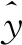
损失函数的计算可以转化为一个优化问题，可以通过最小化损失函数值来匹配分类标签，得到分类结果。

2.3 利用改进Adam优化器的数据优化

使用Adam优化器可以达到更高的训练精度，但是在训练初期，迭代结果存在较剧烈的振荡，鲁棒性较差。合理地调节参数，就能够在一定范围内更好地反映样本的收敛特性。

在样本训练过程中发现，模型的收敛趋势接近幂指数函数变化特点。本文给学习率添加一个修正因子，以下降趋势的幂指数[21]学习率为基础，利用上一阶段的梯度值对其进行调节，达到自适应调节的要求，进而改变网络模型的收敛性能。

幂指数学习率为

η=η0m-k。

(7)

其中：η0表示初始学习率，本文取η0=0.1；m表示迭代中间量，由迭代次数和最大迭代次数确定；k表示超参数，其计算公式为

(8)

其中：λi表示第i次迭代过程中的步长变化率；q为固定常数，一般取值为0.75。

结合梯度更新变化公式，可得第t次迭代学习率更新公式为

(9)

其中：R为最大迭代次数；Lt为第t次迭代梯度值lt和t-1梯度值lt-1的平方和；ε为衰减因子，取值为0.999 9；K为常数项，取值为1。可以看出，本文对学习率的改进是在前一阶段学习率取值的基础上，利用当前阶段的梯度值lt自适应调节。

3 实验结果及分析

从某医院128 772幅临床病理电镜人体组织图像数据库中抽取电镜图像作为实验对象。该数据库包括35 253幅包含原子亮点的阳性图像、93 519幅不含原子亮点的阴性图像，分别从两个数据库中随机抽取3 000幅图像数据进行模型训练。

使用包含输入层、2组由卷积层和池化层交错连接构成的隐含层、优化器、Softmax分类器以及输出层卷积神经网络模型进行实验。

采用基于Google开发的深度学习开源框架TensorFlow作为研究平台，应用Intel(R) Core(TM) i5-8337U CPU@2.8 GHz进行实验。

3.1 图像预处理与训练

选取图像样本作为输入进行训练，为了保证图像特征不丢失，并增强目标特征的表现，需要对样本作预处理。

电镜图像中存在与目标特征无关的噪声因素，可能在传输中产生，也可能在量化等处理中产生，会对网络的训练产生一定的干扰，甚至可能导致训练结果不收敛。需要对整幅图像进行检测、对齐、归一化等处理，增强图像中的目标特征，去除噪声信息。

本文从数据库中随机抽取部分图像作为实验样本。利用图像分割技术得到单独原子图像，电子显微镜拍摄原图如图2所示，通常可以分为两类，表示有或无原子存在。

图2 电子显微镜拍摄的原图

需要对电子显微镜拍摄的原图进行滤波处理。处理效果的好坏将直接影响到后续图像处理和分析的有效性和可靠性。电镜图像经高斯滤波处理后的效果如图3所示。可以看到，经过处理的图像，在尽量保留图像细节特征的条件下对目标图像的噪声进行消除，经过处理的图像，其周围的噪声点有了很大的抑制。

图3 电镜图像滤波处理效果

对经过滤波处理后的电镜图像，需要进行归一化处理。经过归一化处理，可以降低外在干扰因素对图像的影响，减小不确定性。归一化处理后的图像处理效果如图4所示。可以看出图像经过归一化处理后更加平滑、整洁。接下来，对图像进行裁剪变换，去除其在数据分析上无意义的点。

图4 映射变换效果图

经过上述处理后的电镜图像已经具备了进行训练的能力。

3.2 收敛性

采用改进Adam优化器算法优化器对电镜数据集进行训练，并在学习率η分别为0.000 1、0.001和0.01等3种条件下与其他5种优化器进行对比实验。

本文采用分类准确率[22]评价不同分类模型对无标签数据正确分类的概率，区分无标签数据中是否含有原子。数据中含有原子的主要特征是指一张图像中含有一个完整原子亮点，或者含有一个完整原子的绝大部分，则将其视为有原子的数据，否则视为无原子的数据。

由于学习率对网络的分类精度、收敛效果都有影响，因此，本文对不同学习率条件下的算法优化器性能进行次测试。每次实验迭代2 000代，不同学习率训练下的损失函数曲线如图5所示。

图5 不同学习率训练下的损失函数曲线

可以看出，学习率设定对迭代训练的结果影响明显，在不同的学习率设定下，优化器算法的收敛性能通常会有较大的区别。如图5(a)所示，学习率较低时，网络参数更新较慢，损失函数曲线往往在1 500代以后才会开始收敛，收敛速度较慢；在图5(c)中，当学习率较大时，网络参数更新较快，损失函数曲线通常在500代左右就已经开始收敛，收敛速度有了显著提高。

在相同实验条件下，改变数据集规模，在6 000张图像的基础上依次增加100张，对训练样本进行15次实验，观察并记录实验结果，不同算法优化器平均分类精度实验结果对比如表1所示。

表1 6种算法优化器平均分类精度实验结果对比

观察表1可知，本文改进算法在不同数据集规模的样本上进行实验，最大分类精度可达92.3%，分类精度均大于其他算法。并且，随着数据规模的增大，本文方法分类精度的波动较小。具有比其他优化器更理想的分类效果。

对实验结果进行稳定性判别。判别依据是对15次实验中的每次实验每隔100代读取一次数据计算其损失函数方差的大小，损失函数方差的计算公式为

(12)

不同算法相同迭代阶段损失函数方差如表2所示。可以看出，在相同迭代阶段，本文改进算法的损失函数的偏差更小，表现更加稳定。

表2 6算法相同迭代阶段损失函数方差(×10-4)

15次实验中，不同算法收敛点迭代次数如表3所示。

可以看出，本文改进算法到达收敛点所需的迭代次数更少，迭代速度更快。

表3 不同算法收敛点迭代次数

3.3分类精度

采用接受者操作性能(receiver operating characteristic, ROC)[23]曲线分析图像的分类精度。ROC曲线又称为感受性曲线，描述在特定刺激条件下击中概率(true positive rate, TPR)与虚报概率(false positive rate, FPR)的关系。在ROC曲线中，曲线与坐标轴间所围图形下方面积被称为AUC(area under curve)值，AUC的取值反映了算法分类准确性程度，取值范围为0.5～1，AUC与准确性的关系如表4所示。

表4 AUC取值与准确性对照表

实验得到几种不同优化器作用下的ROC曲线如图6所示。

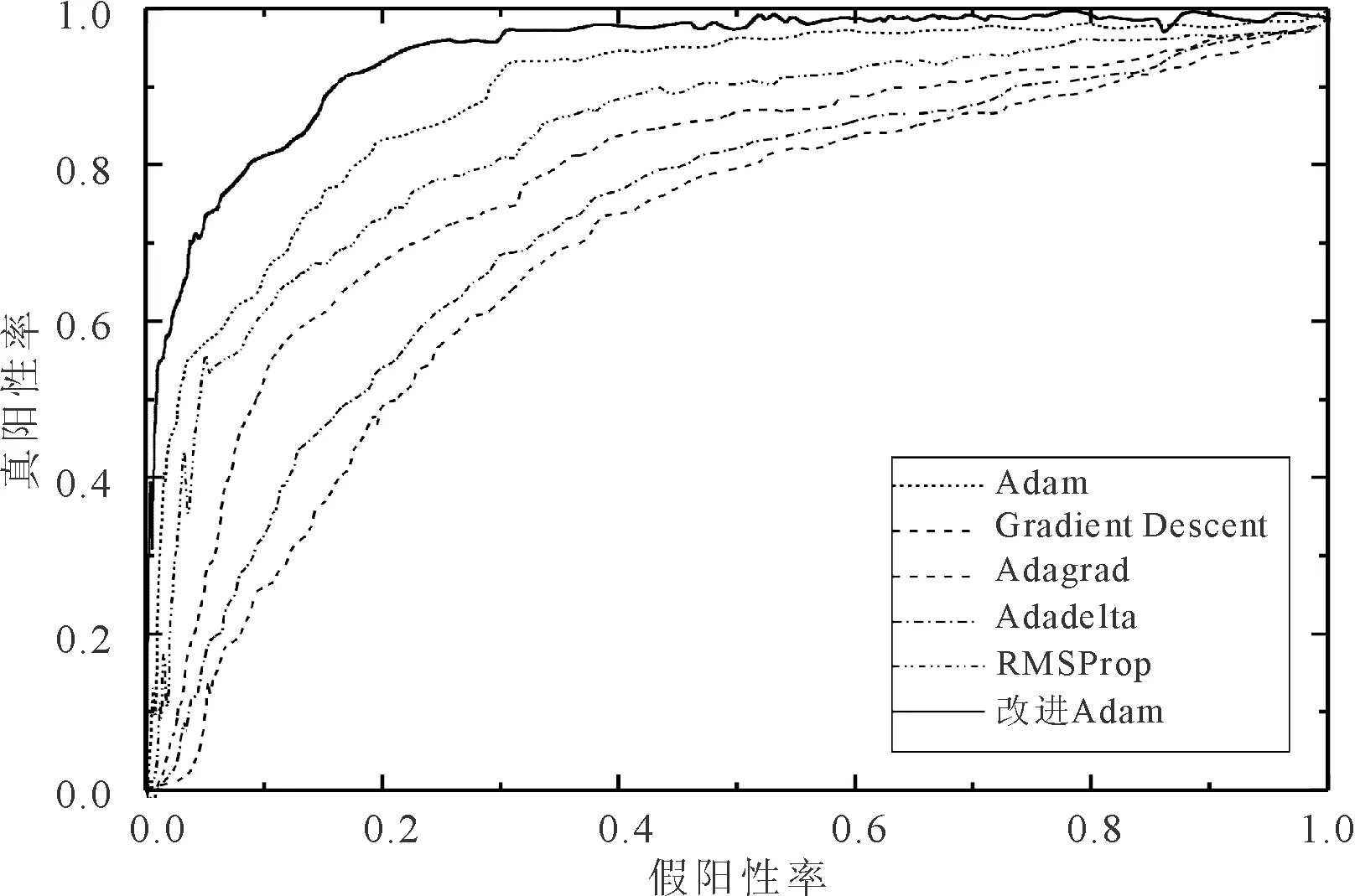
图6 不同优化器的ROC曲线

经过计算、对比几种优化器分类的AUC值可以发现，Gradient Descent优化器的分类特性最差；改进Adam优化器的AUC取值介于0.9～1之间，分类特性最好，相比Adam优化器分类有了较大提高，分类精度较好。

4 结语

针对CNN方法应用Adam优化器算法分类图像时存在的迭代曲线振荡剧烈、收敛性能较差等问题，提出了一种Adam优化器的改进方法。该方法采用具有下降趋势的幂指数学习率改进策略，通过添加修正因子，将上一阶段的梯度值与当前梯度值进行对比、调节，逐次更新学习率的大小，实现优化器学习率的自适应变化。实验结果表明，改进算法最大分类精度可以到达92.3%，并且与原有算法相比，加快模型的收敛速度，增加算法的分类稳定性。