矩阵正态总体下均值估计改进的新方法
刘 薇
(湖南财政经济学院 数学与统计学院,长沙 414205)
1 问题的提出
考虑模型:
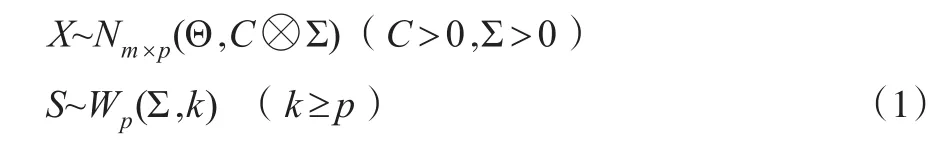
这里假设X与S独立,Θ是m×p阶未知总体正态均值矩阵,C是已知的m阶正定矩阵,Σ是p阶的未知协方差阵,Wp(Σ,k)表示自由度为k,均值为kΣ且维数为p的Wishart分布,符号⊗表示矩阵之间的Kronecker乘积,对于方阵A,A>0表示A是正定矩阵,A≥0表示A是非负定矩阵。模型(1)可看做是MANOVA模型或者多元线性模型[1,2]。
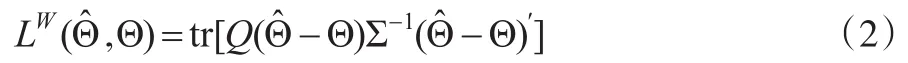
其中权重Q是任意给定的非负定阵。对于Θ的一个估计̂和式(2),本文定义̂的风险为:

基于充分统计量(X,S)并把Σ看做冗余参数,本文将在式(2)下研究均值矩阵Θ的估计的改进问题,并把相关结果应用到协方差的估计的改进问题中去。显然,模型(1)中参数矩阵Θ的最大似然估计是=X。对于Θ的任意一个估计̂,如果RW(̂,Θ)≤RW(,Θ),本文称是最小最大估计。事实上,许多文献考虑了模型(1)中Θ的估计问题。比如:文献[3]考虑了m=1,Q=Im且Σ已知的情形;在Σ未知的情况下,文献[4]处理了m=1,Q=Im的情形;文献[5]研究了p=1,Q=Im且 Σ=σ2(σ2未知)的情形;在Σ未知的情况下,文献[1]考虑了m>p+1,Q=Im的情形;在Σ未知的情况下,文献[2]考虑了p>m+1,Q=Im的情形。上述文献都假设权重Q为单位阵,但是除了文献[6,7]几乎没有相关文献处理Q≠Im情形。然而,权重Q的引入不仅推广了已有的结果,更为重要的是它揭示了均值矩阵估计与协方差阵估计之间的本质关系。文献[8,9]指出了这种关系但他们并没有作进一步的研究。而文献[6]研究了这个问题,但是文献[6]利用正态分布和Wishart的性质仅考虑了Q为对角阵且m>p+1的情形。而这种方法很难用来处理p>m+1的情形。本文将解决这个问题,同时假设Q是任意给定的非负定阵,C是已知的正定阵。本文的主要目的是推广已有文献中的结论。为了加强本文结果的有用性,本文的方法可以用来进一步改良文献[6]中第三部分的结果,因为文献[6]仅考虑了m>p+1的情形下均值估计和协方差估计的关系。
2 Efron-Morris估计的新方法
为了在p>m+1的情形下和更广义损失下改进矩阵均值估计,本文考虑著名的Efron-Morris估计。为了展示在更广义损失下Efron-Morris估计是最小最大估计,需要导出相应风险的无偏估计,这种无偏风险比已有文献中的结果更复杂。在模型(1)下,考虑如下的Efron-Morris估计:
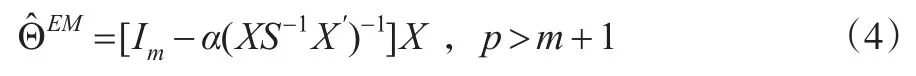
当Q=C=Im时,在式(2)下,文献[2,9]获得了α的最优解为:
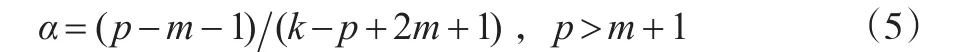
当C=Im,Q:=W=diag(w1,…,wm)时,文献[6]考虑了m>p+1情形下的Efron-Morris估计,并导出了α的最优解,即:
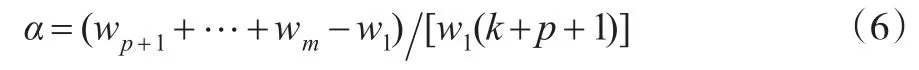
但是他们没有考虑p>m+1下Efron-Morris估计的改良问题。本文只要求在C>0,Q≥0的假设下,研究在p>m+1情形下的Efron-Morris估计。本文的结果推广了已有的结论。
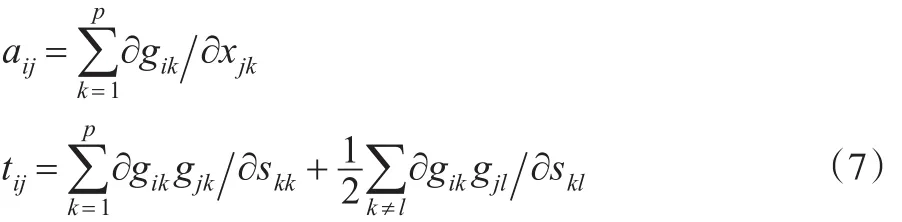
为了获得本文的主要结果,需如下的引理:
引理 1:设对称矩阵A1,B1,C1∈Rn×n的特征根分别为a1≥…≥an,b1≥…≥bn和c1≥…≥cn,则:
①若A1≥0,B1≥0,C1≥0,有:
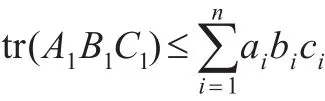
②若A1>0,B1>0,C1>0,有:
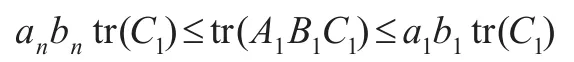
证明:对于①的证明见文献[10]中的定理3,而②中右边的不等式可由①直接获得。因此,只需证明②中左边不等式。由文献[11]中引理1和矩阵同时对角化相关知识,知存在一个正定阵B0,使:
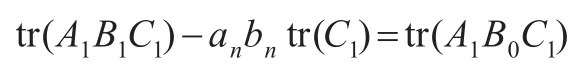
而由文献[12]知,A1B0C1的特征根都是正数。从而引理1成立。
当p>m+1时,本文把Efron-Morris估计式(4)记为:
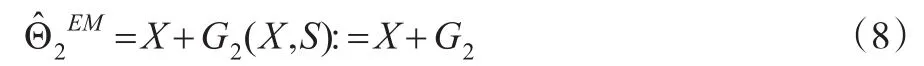
这里G2=-α(XS-1X′)-1X,为了避免引入新的记号,令Am×m:=(aij),Tm×m:=(tij),F=XS-1X′=RLR′,这里aij和tij与式(7)定义相同,L=diag(l1,…,lm),RR′=R′R=Im,R是m×m阶正交阵,l1≥…≥lm≥0是F=(Fij)的特征值,进一步 ,记 ▽X=(∂/∂xij) ,DF=((1+δij)/2)(∂/∂Fij) ,DFg(F)=,这里g(F)是标量,V=V(F)=(vij)是m×q阶矩阵,δij是Kronecker算子。类似地,本文可以定义DS、DSg(s)和DSV。
经过简单的计算,有:
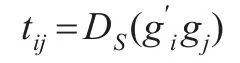
这表明:
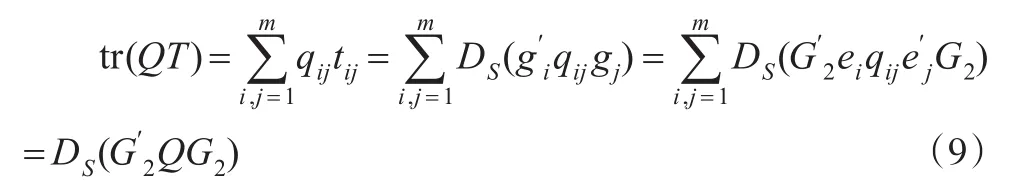
因而,结合式(9)与文献[1]中的推论2.1知,在式(1)和式(2)下的风险的无偏估计具有如下形式:
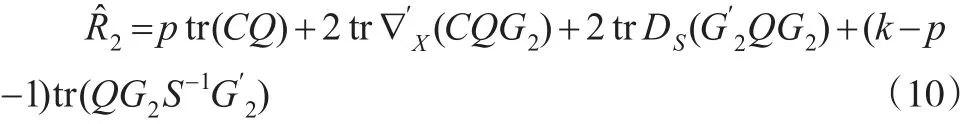
本文将利用式(10)并在一定的条件下证明了p>m+1情形下Efron-Morris估计为最小最大估计。为此,还需要如下引理:
引 理 2:令ϕ(L)=diag(ϕ1(L),…,ϕm(L)) ,R=(R1,R2…,Rm)(Ri是相应于特征值li的特征向量),并假设相关偏导数存在,则:
①DFli=Ri,
③DF[Rϕ(L)R′]=Rϕ1(L)R′,
其中:
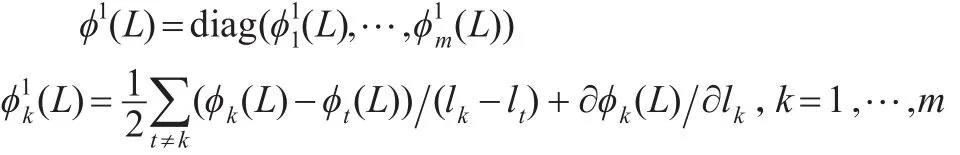
证明:见文献[2]中的引理2.3。
令:
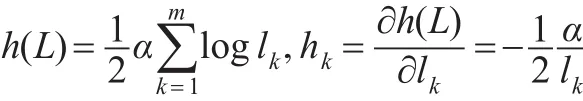
从而:
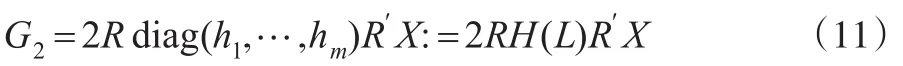
这里H(L)=diag(h1,…,hm)。由文献[2]中引理2.3得:

进一步,由文献[2]中的引理2.2知:

结合式(10)至式(12)有:
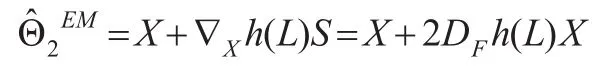
因此,类似于文献[2]中定理2.1的证明并经过简单的计算,无偏风险式(11)可表示为:
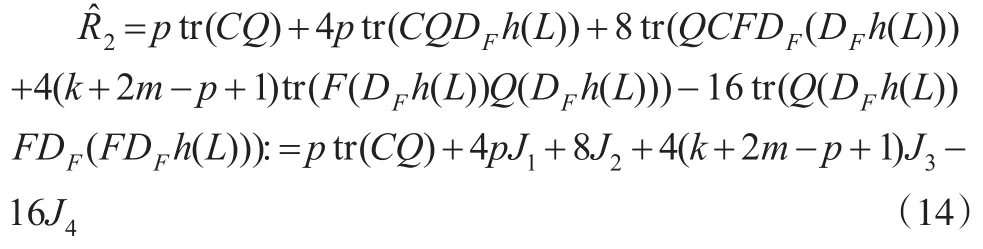
显然,当C=Q=Im时,式(14)即可化简为文献[2]中的结果。
定理1:在模型(1)和式(2)下并假设Q>0,如果α满足:
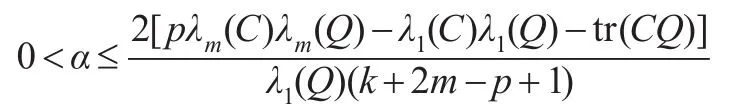
证明:由式(12)知:
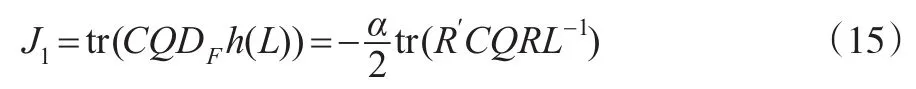
由引理2和式(13),得:
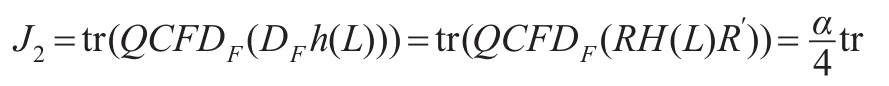
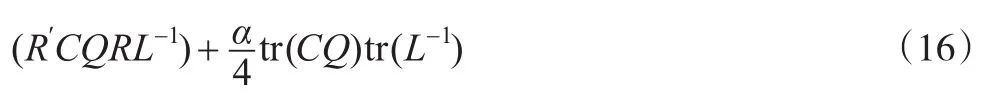
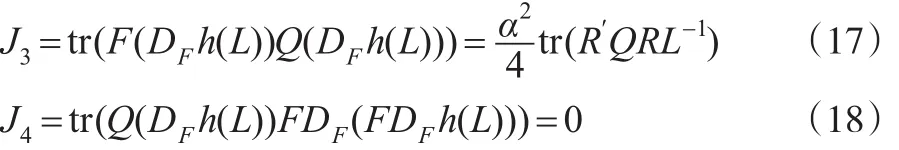
因此,结合式(15)和式(18)知:
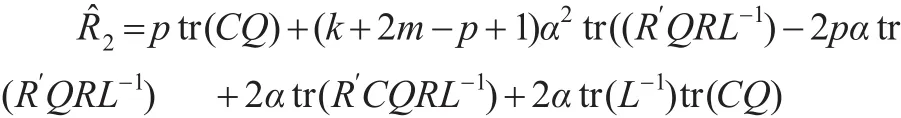
由引理1知:
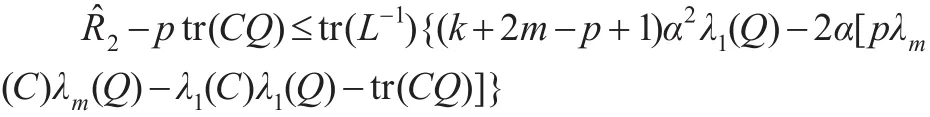
从而定理1成立。
由定理1易知,当C=Q=Im时,α的最优解与文献[2]一致。
3 实例
本文通过一个数值的例子来验证定理1中结果的有效性。假设Θ的每个元素是来自均匀分布的某次抽样,C是一个对角矩阵且每个对角元素是来自标准正态分布的某次抽样,Σ具有一阶自回归结构且一阶系数为0.5,Q具有一阶自回归结构且一阶系数为0.5。进一步,在这个例子中取,显然它满足定理1中的条件。为了比较,考虑不同的参数组合(m,p,k),利用2000次蒙特卡洛模拟去计算相关估计的风险,相关结果被描述在表1中。从表1中的数值结果,可以清晰地观测到改进后的EM估计优于未改进的EM估计和最大似然估计,这与理论分析是一致的。

表1 相关估计的风险结果
4 结束语
本文改良著名的Efron-Morris估计,在C>0,Q≥0的假设下,研究了p>m+1情形下的Efron-Morris估计。并在适当条件下,证明了该Efron-Morris估计是极小极大的。值得说明的是,文献[6]仅考虑了m>p+1的情形下均值估计和协方差估计的关系,下一步打算用本文的结果在p>m+1的情形下建立均值和协方差估计的关系。

