稠油出砂监测器安装位置数值模拟及实验验证
贾宗文 曹砚锋 刘刚 武广瑷 王锴
1. 中海油研究总院有限责任公司钻采研究院;2. 中国石油大学(华东)石油工程学院
适度出砂开采是目前国内外解决稠油生产过程中出砂问题的主要技术,稠油油井出砂的实时监测对适度出砂开采技术的应用具有非常重要的意义[1-4]。通过对油井生产过程中出砂状况进行持续有效的监测,获得实时出砂信息,可为适度出砂开采提供依据,最终指导油井生产,保障稠油高效开发。目前国内外主要采用振动监测方法[5-8]进行出砂监测,其主要由高频压电传感器、信号预处理系统、数据采集系统及计算机软件系统等组成。将高频压电传感器安装在出砂流动管道外壁上,生产过程中,油流携带砂粒以一定的速度撞击管壁,产生振动,高灵敏度传感器感应并接收这些振动信号,通过滤波、放大等预处理,最终传送到计算机信号分析系统,得到出砂量信息,达到实时监测目的,从而为评价出砂状况提供依据。
为了获得准确的出砂监测结果,需要将传感器安装在最有利于接收砂粒撞击管壁振动信号的位置,这需要模拟研究油水砂三相流通过90°弯管(油气井生产主要弯管形式)时的流动状态,确定砂粒经过弯管时撞击力度最大的地方,依此确定传感器的安装位置,以获取最强烈、最准确的出砂振动信号。利用Fluent软件对含砂油流进行了模拟,建立了油水砂三相流通过90°弯管时的流动模型,研究了砂粒撞击管壁的能量最大位置,同时建立了室内出砂监测模拟装置,进行了不同安装位置的室内对比实验,以验证理论模拟结果。
1 模型建立
为更好地了解非牛顿流体油-水-固三相流流经弯管的流动特性,采用Fluent软件进行CFD计算,得到一定含水率下,一定流体黏度、含砂量、流速、砂粒粒径条件下弯管处多相流体流动的特性及固相砂粒运动轨迹。
Fluent软件Mixture模型可以模拟各相不同速度的多相流,也可以模拟各相以相同速度流动的多相流和有强耦合的各相同性多相流[9]。因此,选用Mixture模型研究弯管混合多相流,研究过程中,选用k-ε双方程湍流模型,模拟油水两相流在管道中的流动[10-12]。
1.1 物理模型
利用有限元软件建立室内实验条件下的弯管实体模型,得到网格图如图1所示。模型进口边设为速度进口(velocity-inlet),模型出口边设为自由出口(out-flow),其余边设为管壁(wall)。弯管模型的局部放大图如图2所示。

图1 弯管有限元网格划分图Fig. 1 Finite-element mesh generation diagram of elbow

图2 模拟区域及弯管网格划分示意图Fig. 2 Sketch of simulated area and mesh generation of elbow
1.2 数学模型
固相砂粒在流场中的质量及动量载荷率非常低,连续相(油水相)基本不受离散相(砂粒)的影响,可以忽略砂粒对油水两相流的影响,因此选择非耦合计算;同时,考虑到砂粒与连续相湍流的相互作用及砂粒之间各自运动轨道的干扰,采用随机轨道模型计算。利用Fluent求解离散相问题主要包括以下步骤:(1)设定离散相轨道的迭代步数;(2)创建不同粒径砂粒的属性;(3)选择固相进入的平面及速度、粒径、质量流量等参数;(4)从计算好的油水两相流流场中查看颗粒轨迹。
为进一步确定油水砂多相流中固相砂粒冲击管壁产生最大动能的大致位置,即传感器最适合安装位置,采用Fluent流体力学分析软件对多相流中砂粒在弯管附近的流动状态进行分析[13-14]。
在多相流弯管模拟分析中,认为油-水两相流为连续相,油相均匀分布在水相中;砂粒之间的相互作用采用基于Lagrangian方法的小球模型;忽略黏性损耗,同时考虑重力的影响,得到连续性方程和动量方程
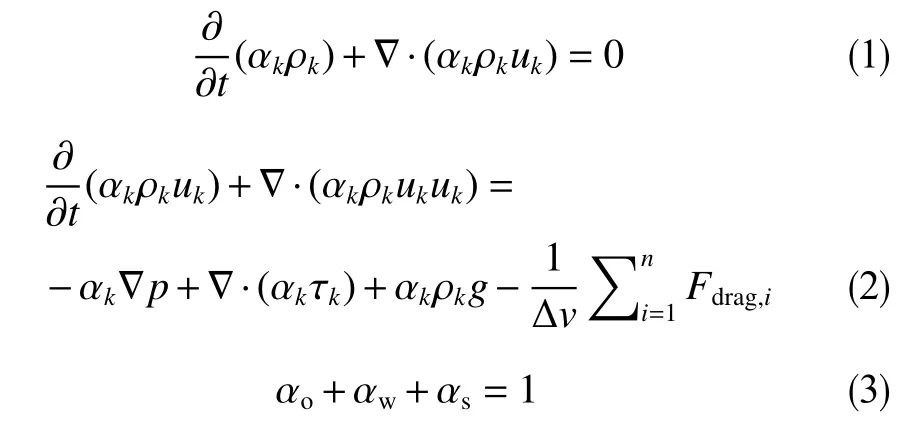
式中,ρ为密度,kg/m³;α为各相体积分数,%;u为流体速度,m/s;p为压力,Pa;g为重力加速度,9.8 m/s²;τ为流体剪切压力,Pa;角标k代表不同的相,o为油相,w为水相,s为砂粒相;Fdrag为不同颗粒流动阻力,N;Δv为体积计算单元;n为网格内颗粒数量。
颗粒之间的运动方程由牛顿第二运动定律决定

式中,mp为颗粒质量,g;up为颗粒速度,m/s。
Fluent离散相模型对多相流中的砂粒流动特性的计算分析流程如图3所示。

图3 油水砂三相流弯管内流动的CFD计算流程Fig. 3 CFD calculation process for the oil-water-sand three-phase flow inside the elbow
2 油水砂三相流动弯管模拟
2.1 模拟条件
采用润滑油模拟,油品黏度为330 mPa · s,液流含水20%,综合黏度200 mPa · s;固相砂粒密度为2 650 kg/m3,砂粒质量分数为0.1 %,粒径大小80~325目(表1),弯管外径30 mm,内径25 mm,弯管曲率半径约为2.5倍内径,流体入口流速为2.2 m/s,出口为自由出口。温度条件26 ℃,环境压力1个大气压,油样密度960 kg/m3。为了保证湍流流体在管路中充分发展,模型的流体入口和出口距离弯曲处均为32倍管内径。

表1 砂粒目数与直径的对应关系Table 1 Corresponding relationship between mesh and diameter of sand grain
2.2 含砂油流中砂粒运动轨迹
分别在80目、100目、150目、200目、325目砂粒粒径条件下,模拟弯管内携砂流体流动,含砂量均为0.1%(质量含量),得到弯管处砂粒的运动轨迹如图4所示。
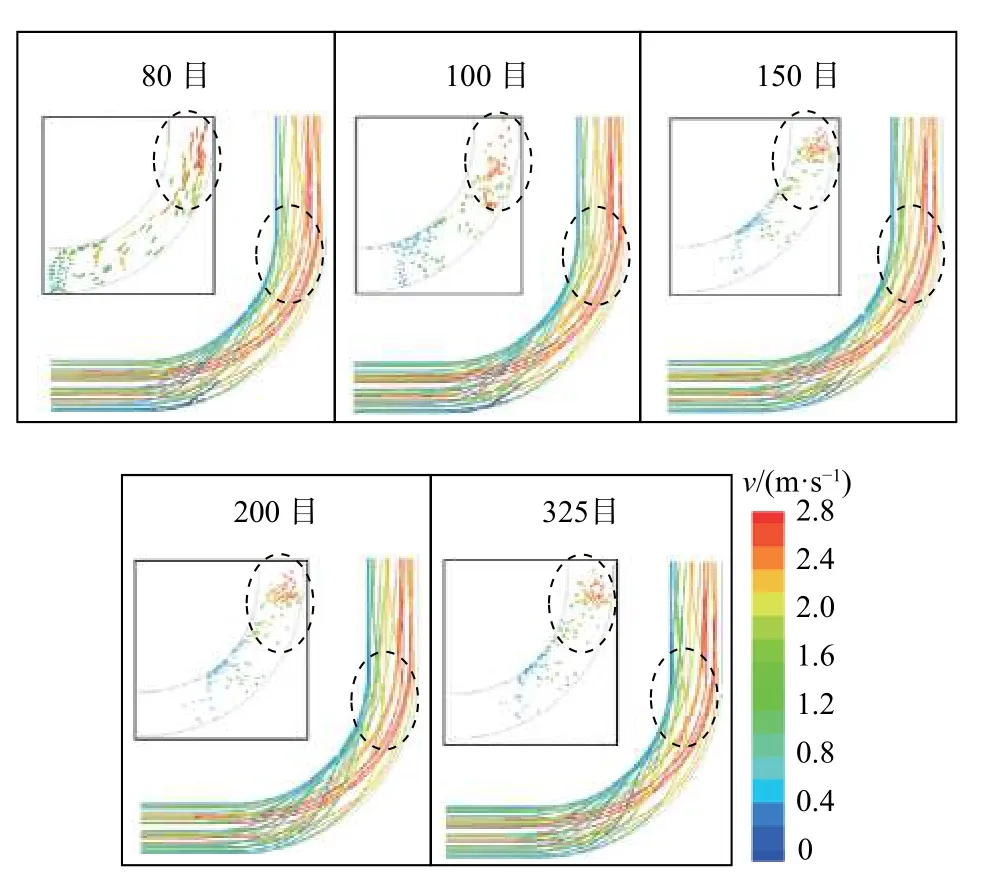
图4 弯管处的不同粒径砂粒在油水砂三相流中的运动速度分布Fig. 4 Distribution of the movement velocity of the sand grains of different sizes in the oil-water-sand three-phase flow in the elbow
针对黏度较高的油水砂多相流体,进一步采用CFD计算方法对弯管处不同尺寸砂粒的速度和轨迹分布进行分析,结果如图4所示。图4中实线为不同尺寸砂粒在弯管内的速度和轨迹分布结果,对于油水砂三相流,不同尺寸砂粒(80~325目)均在弯管下游约2倍管径处速度达到最大值,此时动能最大,因此弯管下游2倍管径处也为监测砂粒撞击信号的传感器最优安装位置。图4中左上角方框内为某时刻,不同尺寸砂粒(80~325目)在弯管内的速度和状态分布图,结果表明无论是80目的大尺寸砂粒,还是325目的小尺寸砂粒均能冲击到管壁上。
3 室内实验验证
在室内条件下,对安装在不同位置的传感器的出砂监测效果进行了对比实验研究,传感器的安装位置分别为弯管处、弯管下游约2倍管径处、弯管下游约3倍管径处。实验条件,采用综合黏度200 mPa · s、含水约20%的油流(主体油流为润滑油),砂样为100目的石英砂,含砂量0.1%,管流速度为2.2 m/s,与Fluent软件模拟条件一致,进行了出砂监测效果对比实验。多相含砂流体出砂监测模拟试验平台见图5,出砂监测传感器安装位置见图6。
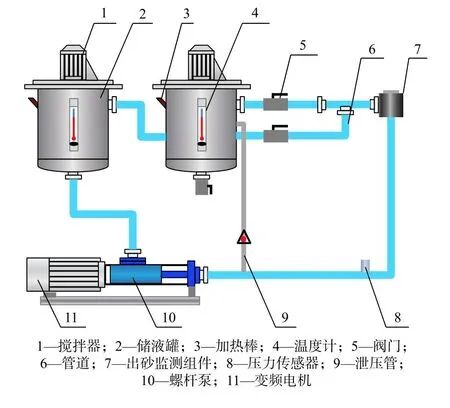
图5 多相含砂流体出砂监测模拟试验平台示意图Fig. 5 Schematic simulation experiment platform for monitoring the sand production of multi-phase sand containing fluid

图6 室内条件下传感器不同安装位置示意图Fig. 6 Schematic installation position of the sensor under indoor conditions
出砂监测实验中,砂粒撞击管壁产生的振动信号实际上是确定性的受振系统在随机力的激励作用下产生振动的过程,因此,出砂振动信号可视为一种随机振动信号。采用振动信号的时频分析理论对实验数据进行了分析处理,流程见图7。图中,T为采样时间间隔,s;N为采样点数;k为傅里叶变化的第k个频谱;X(k)、Y(n)、Z(n)为傅里叶变换函数;x(n)为信号样本函数,-∞<n<+∞;W=exp(-2πj/N),j为虚单位,j2=1;P为功率谱函数。

图7 出砂监测信号数据处理流程Fig. 7 Data processing process of sand production signal
对安装在不同位置传感器采集的出砂振动信号进行时频分析处理,得到出砂监测信号的时频特征值(表2)及功率谱图。分析可得:在其他实验条件均相同的情况下,安装在弯管下游2倍管径处得到的出砂监测信号功率谱幅值最大,信号能量最大,说明在此处砂粒撞击管壁振动最大,验证了多相管流条件下的理论模拟结果。因此,出砂监测传感器的最优安装位置为弯管下游约2倍管径处。
4 结论
(1)利用Fluent软件建立了含砂液流经过90°弯管流动的油水砂三相流模型,模拟了砂粒流经弯管的运动轨迹及速度分布,研究表明,砂粒流经弯管后,在下游方向约2倍管径的位置处撞击管壁的速度最大。
(2)建立了多相含砂流体出砂监测实验平台,进行了不同传感器安装位置的出砂监测实验,结合信号分析结果,表明安装在弯管下游约2倍管径处的监测效果最好,验证了模拟分析结果。因此,传感器安装在此处,可以获得最强的出砂振动信号,从而得到准确的出砂监测数据,指导适度出砂生产。
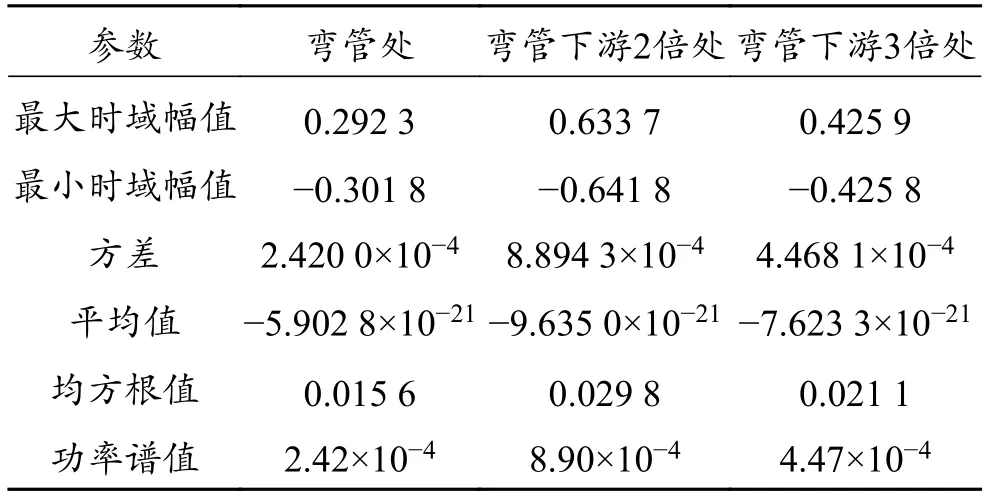
表2 不同安装位置采集的出砂监测信号特征值对比Table 2 Comparison between the characteristic values of thesand production monitoring signals acquired at different installation positions

